多尺度有限元法结合分层网格模拟二维奇异摄动的两端边界层问题

孙美玲，江山

（1.南通职业大学 数学教研室，江苏 南通 226007; 2.南通大学理学院，江苏 南通 226019）

多尺度有限元法结合分层网格模拟二维奇异摄动的两端边界层问题

孙美玲1，2，江山2*

（1.南通职业大学 数学教研室，江苏 南通 226007; 2.南通大学理学院，江苏 南通 226019）

通过摄动系数建立分层网格，用多尺度有限元法捕捉对流扩散方程的两端边界层，研究二维奇异摄动模型。基于分层网格并利用多尺度基函数刻画了边界层的微观信息，用有限的计算资源、较短的计算时间，得到了不依赖于摄动系数、一致稳定的模拟结果。

奇异摄动；自适应网格；两端边界层；多尺度有限元；一致稳定

0 引言

文献［3-9］主要考虑一维奇异摄动的有效求解方法。KADALBAJOO等［3］采用三次B-样条配点法在Shishkin网格上得到了关于最大模的收敛结果。但Shishkin分片等距网格存在一定局限性，粗略估计过渡点位置可能造成方法精度不高。GENG等［4］用再生核方法模拟两端边界层现象；杨宇博等［5］研究非对称内罚间断有限元法在分层网格中的一致收敛性，在一维情形下对左端附近的分层网格进行加密构建。受其启发，本文将其拓展为左右两端附近皆可用自适应迭代的网格，适用于二维情形下的方向。ZHENG等［6］用混合有限差分格式处理拟线性边值问题；基于Bakhvalov-Shishkin网格，江山等［7］、郑权等［8］分别得到多尺度有限元法、混合差分法的奇异摄动高精度结果；CHENG［9］利用局部间断有限元法有效模拟了双参数模型，并基于各范数给出了稳定性估计。

对二维奇异摄动的研究已取得一定成果，如FRANZ等［10］利用单元边界稳定化技术，证明了高阶有限元格式总能得到理想的一致超收敛；BRDAR等［11］面向二维对流反应扩散的双参数方程，基于Duran-Lombardi与Duran-Shishkin网格，用传统双线性有限元法得到了比Shishkin网格精度更高的能量范数误差；JIANG等［12］提出了独立构造试探函数空间、检验函数空间的Petrov-Galerkin多尺度有限元基函数，在等级网格上自动消除共振误差，得到了精确、高效、稳定的一致收敛模拟；LI等［13］针对反应扩散方程，基于分层网格证明了高阶Galerkin有限元的优化理论；XU等［14］、CAI等［15］分别给出了组合有限元、高阶有限元的鲁棒性分析与数值验证，但在二维情形下这类有限元模拟的计算代价较大。

本文针对二维奇异摄动中小参数导致的两端边界层问题，利用基于分层网格的多尺度有限元计算格式，实现较传统有限元计算格式数值精度更高、计算代价更小、运算时间更短的一致稳定结果。

1 模型

考虑二维情形的对流扩散方程

其中，双线性形式为

2 分层网格与解的分解

2.1 两端边界层的分层网格

为得到式（2）变分形式的有效近似，用有限维逼近无限维的思想进行区域离散。因常规的一致网格难以有效求解奇异摄动小参数问题，即使剖分数很大，其等距步长也无法满足，故难以形成可靠的分辨率。对二维区域，先在方向形成适合左右两端边界层的优化分层网格，再类似处理方向的上下两端边界层。

分层（graded）网格［5］由迭代格式生成，用摄动系数和网格参数计算。方向的节点为

从而形成一端稠密、另一端稀疏的分层网格。为满足两端均有边界层的情况，将式（3）改进为

下文将验证分层网格是一种能自适应地逼近边界层位置及宽度的优化网格，其剖分数并非简单地成倍增加，从而突破了一致网格和Shishkin网格剖分数偶数倍加密的局限，得到了更好的数值精度与稳定结果。

2.2 解的多尺度分解

依据解的多尺度性质，将其分解为若干部分之和，即

用式（4）对两端边界层的分层网格进行区域离散，再采用多尺度有限元计算格式，使其更好地逼近子分块上多尺度解式（5）的局部形态。

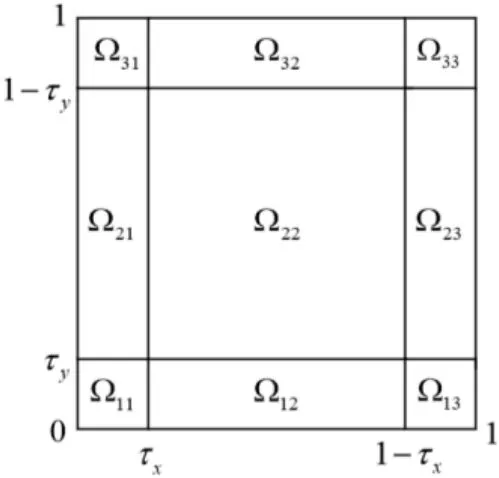
图1 区域的子分块Fig.1 Sub-domains of domain

3 有限元法与多尺度有限元法

3.1 有限元的变分原理

传统有限元法（FEM）通过分片多项式构造基底以形成有限维函数空间。如选定一组基，记有限元空间，其变分形式对应为寻求，使得

3.2 多尺度有限元的变分原理

不同于传统有限元，多尺度有限元法（MsFEM）在构造有限维空间时，不采用显式多项式函数，而采用基于与原问题相同的微分算子在粗风格单元中求解非显式基函数。在每个粗网格单元中用有限元法求对应的齐次子问题：

3.3 多尺度有限元解的误差估计

度量误差，结合分层网格得到收敛结果。

定理1

为二维分层网格的生成函数。

4 数值验证

用已有文献算例和程序结果验证相应方法的精度和效率，本文仅讨论当很小时产生奇异摄动边界层求解困境的情况。将分层网格上与传统有限元、多尺度有限元对应的结果分别记作FEM（G）和MsFEM（G），用真解、近似解和误差的三维图示、范数值分析度量实际模拟效果。

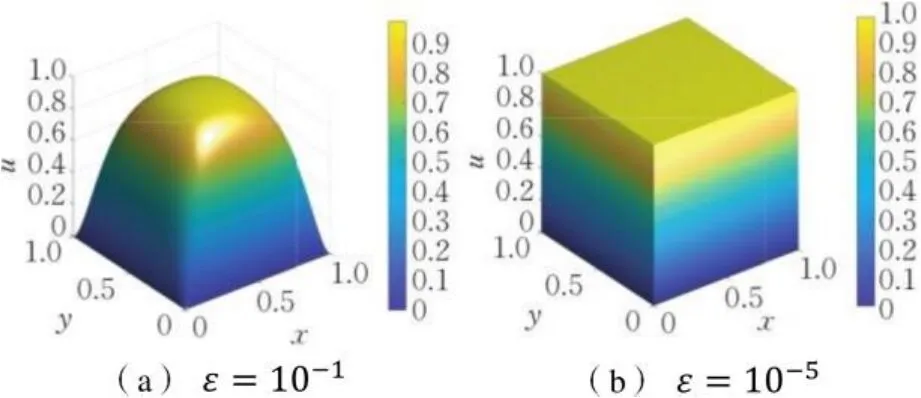
图2 当=时的真解Fig.2 Exact solutions when and ，respectively

图3 当时传统有限元法与多尺度有限元法的解Fig.3 The solutions of FEM（G）and MsFEM（G） when

为更清晰地展现相应方法的精确性与稳定性，通过网格加密的方法观察数值变化。表格格式与文献［5］的表1与表2一致，区别在于文献［5］处理的是一维问题，行数较多、单方向剖分数较小，本文研究的是二维问题，因受算力限制，行数较少、单方向两端边界层的剖分数较大。由表1知，无论摄动参数如何选取，依据网格参数的递减，由迭代式（4）自适应生成两端疏密不同的分层网格，用于离散化计算。横向看，表1中单方向剖分数、范数误差均微增，纵向看，其范数误差随递减呈稳定收敛。表1为用传统有限元法求解二维问题，若网格剖分数较大，计算消耗很大，继续剖分将超出单机的运行限定，具有一定的局限性。表2采用的是多尺度有限元法，仅在较粗的分层网格上计算误差的能量范数，求式（7）时其子单元剖分数，对应行的精度略逊于表1，但其计算消耗小、时间短，继续剖分能得到更精确的结果，其收敛结果与理论估计式（12）一致。另需指出，多尺度有限元法的精度在剖分数=222，262，300时较传统有限元法在剖分数=240，288，328时更高。当然此优化结果也有计算消耗，主要用以刻画奇异摄动问题的边界层微观属性。

表1 不同下传统有限元法在分层网格上的误差能量范数Table 1 FEM（G）with different parameters for errors of energy norm

表1 不同下传统有限元法在分层网格上的误差能量范数Table 1 FEM（G）with different parameters for errors of energy norm

h误差误差误差1364.510×10-31604.664×10-31924.748×10-32401.310×10-32881.362×10-33281.402×10-34483.870×10-45364.054×10-46164.189×10-48881.083×10-41 0481.142×10-41 2001.186×10-4

表2 不同下多尺度有限元法在分层网格上的误差能量范数Table 2 MsFEM（G）with different parameters for errors of energy norm

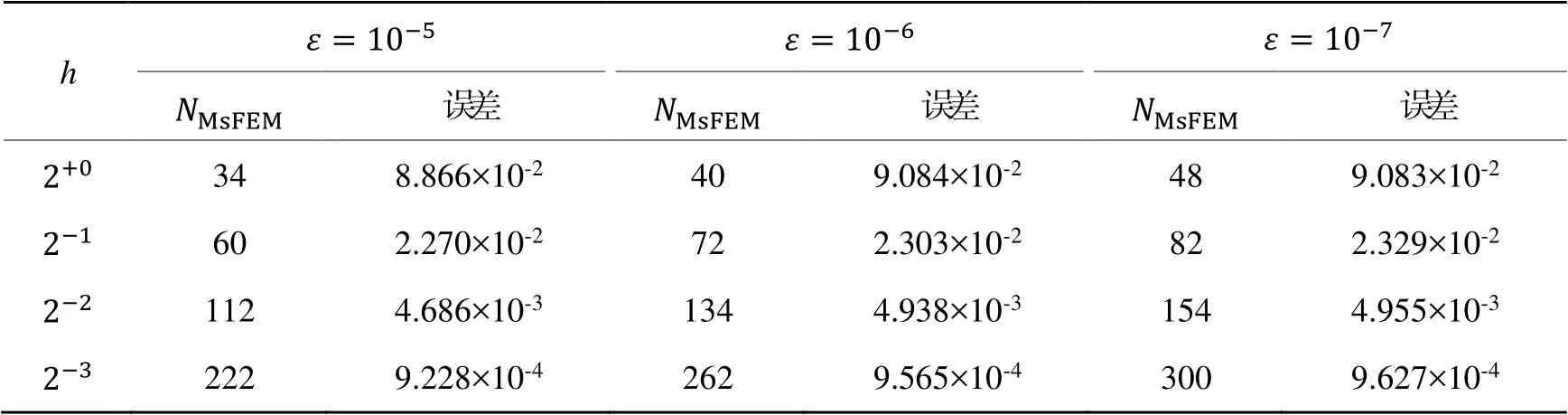
表2 不同下多尺度有限元法在分层网格上的误差能量范数Table 2 MsFEM（G）with different parameters for errors of energy norm

h误差误差误差348.866×10-2409.084×10-2489.083×10-2602.270×10-2722.303×10-2822.329×10-21124.686×10-31344.938×10-31544.955×10-32229.228×10-42629.565×10-43009.627×10-4

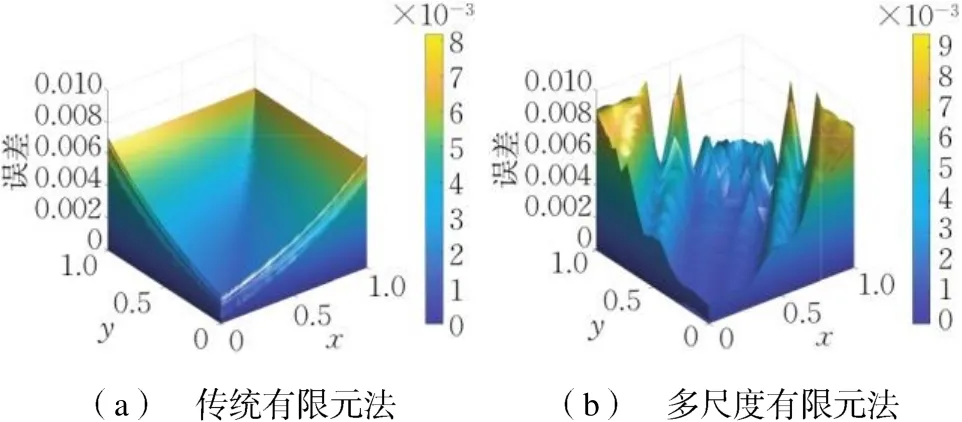
（a） 传统有限元法（b） 多尺度有限元法

图4 当时传统有限元法于和多尺度有限元法于的误差
Fig.4 Errors of FEM（G） onand MsFEM（G）onwhen

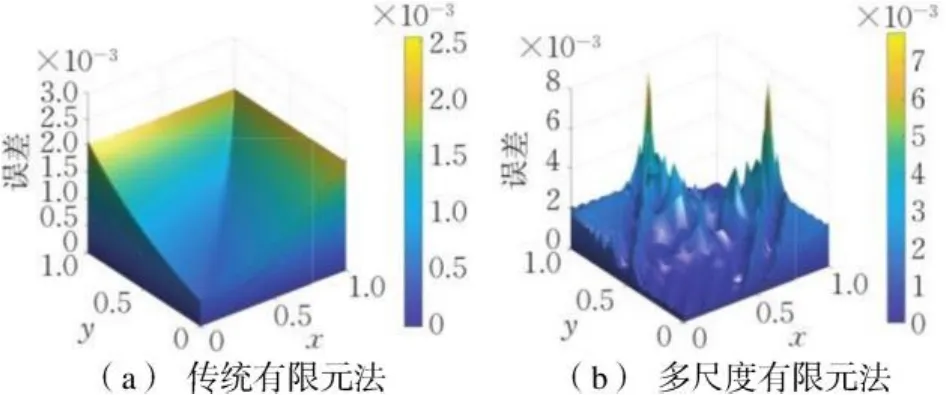
图5 当时传统有限元法于和多尺度有限元法于的误差Fig.5 Errors of FEM（G） on and MsFEM（G）on when

在上述数值精度与稳定分析的基础上，考虑2种数值方法所需的运行时间和效率，表3给出了当时台式机Intel Core i9 CPU 3.7 GHz运行相应程序所需的CPU时间，可见在较密二维网格上用传统有限元法所需的CPU时间是同一行较粗二维网格用多尺度有限元法的近10倍，显然多尺度有限元法的计算效率更高。进一步，图6为摄动参数取更小（与）时相应方法的CPU时间与剖分数的对数比例关系，再次证实了多尺度有限元法的计算代价更小、计算效率更高。

表3 当时传统有限元法与多尺度有限元法的CPU时间Table 3 FEM（G）and MsFEM（G）apos;s CPU time when

表3 当时传统有限元法与多尺度有限元法的CPU时间Table 3 FEM（G）and MsFEM（G）apos;s CPU time when

FEM（G）CPU时间/sMsFEM（G）CPU时间/s4.13.349126598410 2771 106

图6 =和时2种方法的剖分数与CPU时间的log-log图示Fig.6 Two methodsapos; log-log on partition and CPU time when and

综上所述，多尺度有限元法只需在较粗分层网格上进行计算，消耗的计算资源较少，且能保证稳定收敛的有效精度，因此，多尺度有限元法在高维奇异摄动问题求解中具有广阔的应用前景。

5 结束语

基于自适应的分层网格生成机制，主要利用多尺度有限元法处理奇异摄动的二维对流扩散变系数方程。用分层迭代精确逼近边界层位置与宽度，结合多尺度计算格式有效捕捉了两端边界层的微观信息，实现了不依赖摄动系数的精确高效模拟结果，充分展现了多尺度有限元法结合分层网格求解高维奇异摄动问题的一致稳定性和优势。

［1］苏煜城，吴启光. 奇异摄动问题数值方法引论［M］. 重庆：重庆出版社， 1991.

SU Y C， WU Q G. An Introduction to Numerical Methods for the Singular Perturbation Problems［M］. Chongqing： Chongqing Publishing House，1991.

［2］MILLER J J H， O’RIORDAN E，SHISHKIN G I. Fitted Numerical Methods for Singular Perturbation Problems （Revised Edition）［M］. Singapore： World Scientific，2012.

［3］KADALBAJOO M K， GUPTA V. A parameter uniform B-spline collocation method for solving singularly perturbed turning point problem having twin boundary layers［J］. International Journal of Computer Mathematics， 2010，87（14）：3218-3235.

［4］GENG F Z， QIAN S P. Reproducing kernel method for singularly perturbed turning point problems having twin boundary layers［J］. Applied Mathematics Letters， 2013，26（10）：998-1004. DOI：10.1016/j.aml.2013.05.006

［5］杨宇博，祝鹏，尹云辉. 分层网格上奇异摄动问题的一致NIPG分析［J］. 计算数学，2014， 36（4）：437-448.

YANG Y B， ZHU P，YIN Y H. Uniform analysis of the NIPG method on graded meshes for singularly perturbed convection-diffusion problems［J］. Mathematica Numerica Sinica， 2014，36（4）： 437-448.

［6］ZHENG Q， LI X Z，GAO Y. Uniformly convergent hybrid schemes for solutions and derivatives in quasilinear singularly perturbed BVPs［J］. Applied Numerical Mathematics， 2015，91： 46-59. DOI：10. 1016/j.apnum.2014.12.010

［7］江山，孙美玲. 多尺度有限元结合Bakhvalov-Shishkin网格法高效处理边界层问题［J］. 浙江大学学报（理学版），2015， 42（2）：142-146. DOI：10. 3785/j.issn.1008-9497.2015.02.004

JIANG S， SUN M L. Combining the multiscale finite element and Bakhvalov-Shishkin grid to solve the boundary layer problems［J］. Journal of Zhejiang University （Science Edition）， 2015，42（2）： 142-146. DOI：10.3785/j.issn.1008-9497.2015.02.004

［8］郑权，刘颖，刘忠礼. 奇异摄动问题在修正的Bakhvalov-Shishkin网格上的混合差分格式［J］. 浙江大学学报（理学版）， 2020，47（4）： 460-468. DOI：10. 3785/j.issn.1008-9497.2020.04.009

ZHENG Q， LIU Y，LIU Z L. The hybrid finite difference schemes on the modified Bakhvalov-Shishkin mesh for the singularly perturbed problem［J］. Journal of Zhejiang University （Science Edition）， 2020，47（4）： 460-468. DOI：10.3785/j.issn.1008-9497.2020. 04.009

［9］CHENG Y. On the local discontinuous Galerkin method for singularly perturbed problem with two parameters［J］. Journal of Computational and Applied Mathematics， 2021，392： 113485. DOI：10. 1016/j.cam.2021.113485

［10］FRANZ S， LINß T，ROOS H G， et al. Uniform superconvergence of a finite element method with edge stabilization for convection-diffusion problems［J］. Journal of Computational Mathematics， 2010，28（1）： 32-44. DOI：10.4208/jcm.2009.09-m1005

［11］BRDAR M， ZARIN H，TEOFANOV L. A singularly perturbed problem with two parameters in two dimensions on graded meshes［J］. Computers and Mathematics with Applications， 2016，72（10）：2582-2603. DOI：10.1016/j.camwa.2016.09.021

［12］JIANG S， PRESHO M，HUANG Y Q. An adapted Petrov-Galerkin multi-scale finite element method for singularly perturbed reaction-diffusion problems［J］. International Journal of Computer Mathematics， 2016，93（7）： 1200-1211. DOI：10.1080/00207160. 2015.1041935

［13］LI Z W， WU B，XU Y S. High order Galerkin methods with graded meshes for two-dimensional reaction-diffusion problems［J］. International Journal of Numerical Analysis and Modeling， 2016，13（3）： 319-343.

［14］XU S P， DENG W B，WU H J. A combined finite element method for elliptic problems posted in domains with rough boundaries［J］. Journal of Computational and Applied Mathematics， 2018，336： 235-248. DOI：10.1016/j.cam.2017.12.049

［15］CAI D F， CAI Z Q，ZHANG S. Robust equilibrated a posteriori error estimator for higher order finite element approximations to diffusion problems［J］. Numerische Mathematik， 2020，144： 1-21. DOI：10.1007/s00211-019-01075-1

Simulation of multiscale finite element method on graded meshes for two-dimensional singularly perturbed twin boundary layers problems

SUN Meiling1,2, JIANG Shan2

（1. Department of Mathematics，Nantong Vocational University，Nantong226007，Jiangsu Province，China；2. School of Science，Nantong University，Nantong226019，Jiangsu Province，China）

To solve a two-dimensional singularly perturbed model, a multiscale finite element method on graded meshes built from the perturbed parameter is presented for capturing the twin boundary layers of convection-diffusion equations effectively. Based on the graded meshes, the multiscale basis functions are capable of subtly describing the microscopic information in the boundary layers. No wonder, it just costs a handful of computing resource and short time to achieve the accurate and efficient results, and the results are independent of the perturbed parameter with uniform stability.

singular perturbation; adaptive meshes; twin boundary layers; multiscale finite element; uniform stability

O 241.82

A

1008⁃9497（2022）05⁃564⁃06

2021⁃08⁃24.

南通市基础科学研究指令性项目（JC2021123）；国家自然科学基金面上项目（11771224）；江苏省高校青蓝工程优秀骨干教师资助项目.

孙美玲（1981—），ORCID：https：//orcid.org/0000-0003-0061-5155，女，博士，副教授，主要从事偏微分方程数值解及其应用研究，E-mail：sunmeiling81@163.com.

通信作者，ORCID：https：//orcid.org/0000-0001-7983-0012，E-mail：jiangshan@ntu.edu.cn.

10.3785/j.issn.1008-9497.2022.05.007