圆柱形炸药空爆在近场空间的超压估算公式

刘军，王政，熊俊，殷建伟

（北京应用物理与计算数学研究所，北京 100094）

高能炸药在空气中起爆后炸药爆轰波冲击空气界面形成向外传播的空气冲击波，而空气中超过常压部分的压力流场即为空爆超压场. 该超压场是爆炸毁伤效应和防护结构设计的重要输入条件[1-4]，针对空爆超压场的深入研究可为目标毁伤和防护设计提供更为准确的输入. 在远场（等效衰减距离R¯ ≥5m/kg1/3）情况下，由于空爆冲击波压力峰值已衰减至10-1MPa 量级且冲击波形和强度受初始装药形状、起爆方式等因素的影响较小，所以在远场情况下一般将模型简化为等效TNT 当量下的球形装药中心起爆进行建模和分析研究[5-7]. 在近场（R¯ ≤5 m/kg1/3）情况下，相关实验与模拟研究[8-10]均表明装药形状、起爆方式等对近场的压力流场具有较大影响，这些因素对空爆冲击波流场的超压及冲量[11-15]的影响不可忽略. 目前公开发表的研究中针对非球形装药近场空间空爆超压场的可预测性模型研究极少.

对于非球装药研究较多的为圆柱形装药. 圆柱装药在近场的空爆冲击波较球形装药下复杂得多，在不考虑非轴起爆情况下圆柱装药空爆会形成一种典型二维轴对称非均匀分布流场. 已有学者针对圆柱装药空爆的特点、等效等方面开展了相关实验和模拟研究工作[16-38]. PLOOSTER[19]在圆柱装药空爆实验中测量了近场空间不同角度、不同等效衰减距离上的超压. 在该实验测量结果中看到，在长径比L/D= 1/4 及 较 小 等 效 衰 减 距 离（R¯=1.3, 2.0 m/kg1/3）情况下圆柱不同角度上的超压差异极大，0°上的超压较圆柱90°方向高出约一个量级. 由于圆柱装药空爆在近场空间存在复杂波系相互作用及超压在强度、分布上的极度不均匀，所以从理论和实验上提出圆柱空爆近场超压模型均具有较大困难.

针对圆柱形炸药空爆，本文给出了一种适用于近场空间的超压估算公式. 首先，通过球形装药空爆模拟结果与Henrych 经验公式对比，初步验证了空爆模拟的可靠性；之后，模拟得到了圆柱装药在三种不同长径比下的空爆流场，并通过与实验结果对比进一步验证了模拟的可靠性；最后，以模拟结果补足了数据样本空间，拟合得到了圆柱装药空爆近场超压估算公式，并给出了估算公式与实验结果的回归验证.

2,4,6-三硝基甲苯（TNT）是最常用的炸药之一，不同种类炸药空爆一般可等效为TNT 当量，其中空爆超压和冲量也可作类似等效[16,23-25]. 本节对球形与圆柱形装药下的TNT 炸药空爆进行模拟，并分别与经验公式和实验结果进行对比来验证模拟的可靠性.

1 TNT 空爆近场超压的模拟与正确性验证

1.1 球形装药空爆近场超压的模拟与验证

式中：取状态方程参数r=1.4；设置1 atm 下的空气初 始密 度 为 ρ0,air=0.001 225 g/cm3；初 始 压 力 为p0=0.101 MPa，并由式(4)可得到空气初始内能e0.

按表1 中TNT 初始密度计算，1 kg 球形TNT 装药 半 径 为5.271 cm；10 kg 球 形TNT 装 药 半 径 为11.356 cm. 图1(a)给出了1,10 kg 球形装药下不同衰减距离上的空气冲击波压力峰值曲线. 图1(b)给出了图1(a)中红色五角星位置（对应时刻起爆后2 ms）的压力（黑色线内标识了炸药的初始界面）. 表2 给出了图1(a)中不同衰减距离下压力峰值模拟结果与Henrych 经验公式的误差. 由模拟结果与Henrych 经验公式对比来看，不同装药质量的球形空爆冲击波压力峰值曲线在较小等效衰减距离（R¯ ≤5 m/kg1/3）情况下能够较好符合，且球形装药模拟下的气体激波对称性较好. 本文球形装药空爆在近场空间超压的模拟具有一定置信度.

表1 TNT 炸药JWL 参数[36]Tab. 1 The JWL parameters of TNT[36]

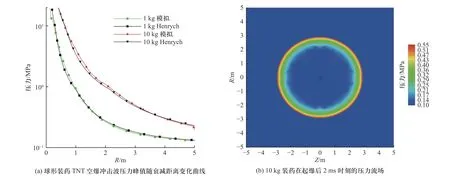
图1 球形装药TNT 空爆冲击波压力峰值随衰减距离变化曲线及10 kg 装药在起爆后2 ms 时刻的压力流场Fig. 1 The peak pressure of spherical charge TNT air blast with attenuation distance and the pressure of 10 kg charge at 2 ms after initiation

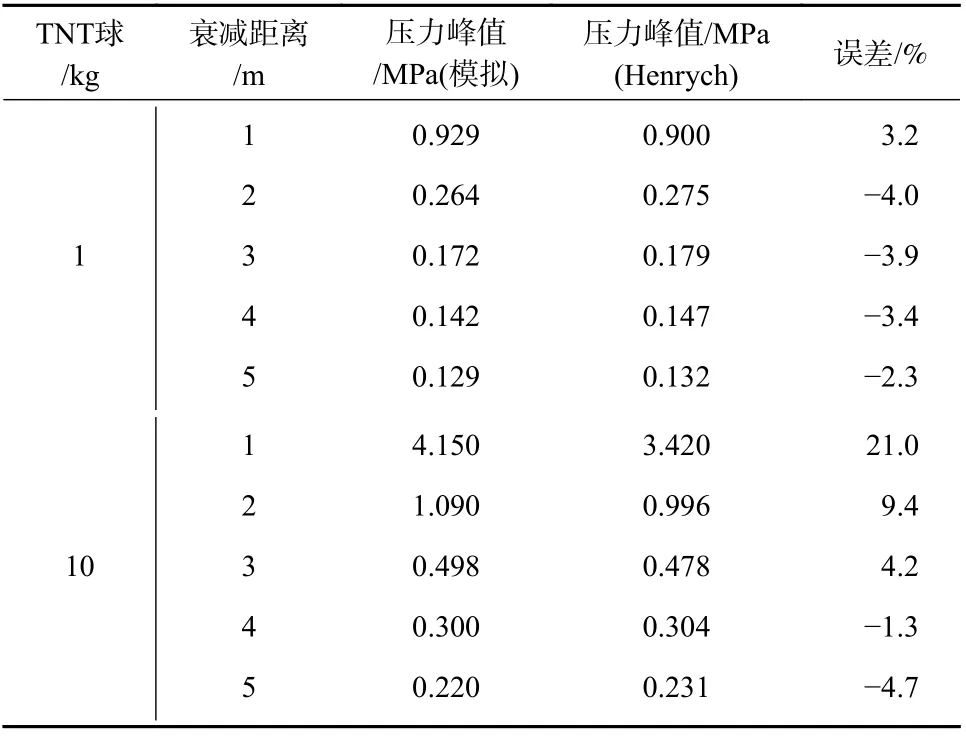
表2 球形空爆在不同衰减距离下压力峰值模拟结果与Henrych 经验公式的对比Tab. 2 Comparison of peak pressure of spherical charge TNT air blast at different attenuation distances

1.2 圆柱装药空爆近场超压的模拟与验证

在保持上节模拟中的模型、参数不变基础上，本节将10 kg 球形装药改为长径比分别为L/D=1/4,1,4的圆柱形装药进行模拟. 其中，在L/D=1/4情况下10 kg 的TNT 圆柱近似取为L=8 cm,D=31.25 cm；在L/D=1情况下10 kg 的TNT 圆柱近似取为L=20 cm,D=19.76 cm；在L/D=4情况下10 kg 的TNT 圆柱近似取为L=50 cm,D=12.50 cm. 模拟并统计了不同角度、不同衰减距离上的压力峰值,将圆柱旋转轴线方向记为0°、轴线垂直方向记为90°方向，角度统计间隔为15°. 图2 给出了三种不同长径比圆柱形TNT 空爆在小等效衰减距离(0 .2 ≤R¯ ≤2 m/kg1/3)上的超压随角度变化的模拟结果.

图2 圆柱形TNT 装药空爆在小等效衰减距离上的超压随角度变化模拟结果Fig. 2 Overpressure with angle of cylindrical charge TNT air blast at small equivalent attenuation distance

下面需要对图2 模拟结果的正确性进行验证. 文献[19]中的表3 给出了圆柱形Pentolite 炸药（一种TNT 基炸药，初始密度1.64 g/cm3）空爆的较完备的近场超压实验结果. 实验中圆柱装药长径比分别为L/D≈1/4,1,4；实验测量给出了9 个角度在2 个等效衰减距离(R¯=1.3&2.0 m/kg1/3)空间位置上的超压.使用该组实验数据[19]，通过将Pentolite 炸药超压以1.11 倍[23]等效TNT 超压转换后，与本文图2 模拟结果进行对比. 图3 给出了三种长径比圆柱装药在R¯ ≈1.3 m/kg1/3位置上不同角度超压的实验结果（黑色散点）与模拟结果（红色点线）的比对. 图4 给出了三种长径比圆柱装药在R¯ ≈2.0 m/kg1/3位置上不同角度的超压的实验结果（黑色散点）与模拟结果（红色点线）的对比.

表3 三个长径比情况下量纲一超压函数的拟合参数Tab. 3 Fitting parameters of dimensionless overpressure function under three length-diameter ratios

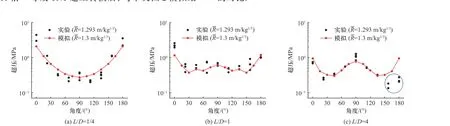
图3 等效衰减距离 R¯ ≈1.3 m/kg1/3 位置上不同角度的超压Fig. 3 Overpressure with angle at the equivalent attenuation distance R¯ ≈1.3 m/kg1/3

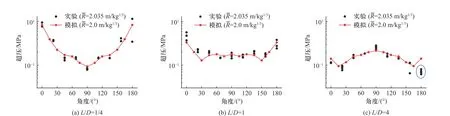
图4 等效衰减距离 R¯ ≈2.0 m/kg1/3 位置上不同角度的超压Fig. 4 Overpressure with angle at the equivalent attenuation distance R¯ ≈2.0 m/kg1/3

需要指出，若此时使用球形装药空爆的式(2)得到的超压预测线为图3、图4 中某一位置上平行于横轴的直线，则显然误差较大、置信度极低，无法满足近场毁伤效应或防护效果的精细评估需求. 而通过圆柱空爆建模及模拟得到的图3、图4 中的模拟结果曲线能够很好地反映各个角度上的实验散点分布特征. 除0°与180°两个角度外，模拟结果与实验散点均值的最大误差约45%（图4(c)中90°位置）. 本文认为，由于近场空间超压在短时间内由102MPa 降至10-1MPa 量级（迅速下降约3 个数量级，参见图2），所以即使在引入上述最大误差棒的情况下本文圆柱炸药空爆近场超压的模拟结果仍然具有较高置信度.

图3、图4 中蓝色虚线内为与模拟结果偏差较大的实验点. 其中，图3(c)在180°方向上的超压模拟结果为0.95 MPa，实验均值约0.23 MPa；图4(c)在180°方向上的超压模拟结果为0.14 MPa，实验均值约0.07 MPa. 分析认为180°附近位置上模拟与实验的误差主要来自于以下几点：

①实验中圆柱装药为某一端面中心点起爆，而模拟中为体心一点起爆. 理论上讲，端面中心起爆必然造成0°与180°压力不对称. 随着等效衰减距离逐渐增加，0°与180°方向压力差异才会逐渐减弱. 已有研究表明不同起爆方式（端面中心一点起爆或两端面中心两点起爆[9,13,19,22]）会影响近场局部方向超压值.

②文献[19]中已指出多组实验结果自身的分散性较大. 由于近场超压值范围(10-1～102]跨度较大，该类实验在不同压力段的测试诊断精度会对实验结果造成较大影响.

③这里使用的Pentolite 炸药空爆超压与TNT炸药空爆超压的1.11 倍等效关系为某一超压段的等效均值[23]. 但在较广的等效衰减距离范围内考虑，该等效关系应不是常量. 这可能造成图3、图4 中的模拟与实验数据间的对比在纵坐标上存在一定的平移偏差.

对于同一时刻而言，圆柱装药空爆流场体现为气体激波的空间形貌不同. 图5 给出了图2(a)中圆柱L/D=1/4 模型在炸药体心一点起爆后不同时刻压力流场的模拟结果（黑色线框内标识炸药初始外界面）. 随着时间逐渐增加，L/D=1/4 的药柱由90°方向传播较快逐渐转变为0°方向传播较快，从而存在气体冲击波由扁椭球至高椭球的形貌转换. 该气体激波空间形貌转换现象是复杂波系（在多次聚心反射后）相互作用的结果，在图2(a)中体现为90°方向超压先高后低、0°方向超压先低后高. 记0°方向与90°方向的超压比为λ. 图6 给出了L/D=1/4 情况下λ随等效衰减距离的变化关系. 图6 中的两个黑色点分别对应图3(a)与图4(a)中0°与90°上超压实验点均值的比. 实验和模拟均表明，圆柱装药情况下在近场的超压比随等效衰减距离变化极大.

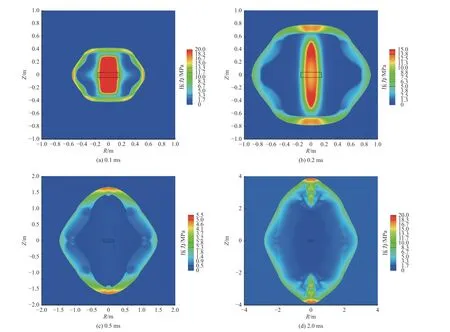
图5 圆柱L/D=1/4 的10 kg 装药TNT 空爆模拟得到的不同时刻的压力流场（黑线标识了炸药的初始外界面）Fig. 5 Pressure at different times obtained from the 10 kg TNT air blast simulation with L/D=1/4 (the black line marks the initial outer surface of TNT)

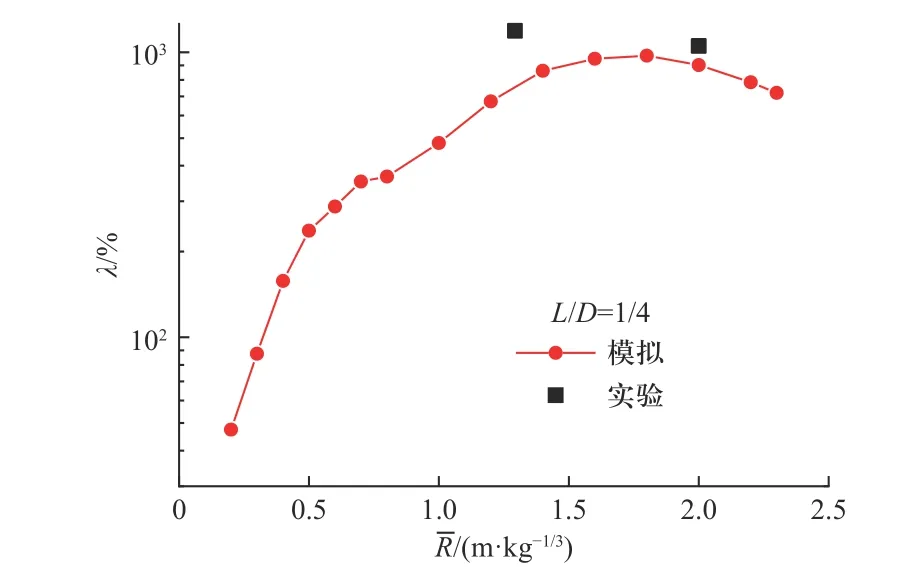
图6 圆柱L/D=1/4 装药TNT 空爆在0°与90°方向的超压比随等效衰减距离变化Fig. 6 Overpressure ratio of cylindrical charge TNT air blast in the direction of 0° and 90° varies with the equivalent attenuation distance

如此大的超压强度差异必然会对近场不同角度、不同衰减距离上炸药空爆的毁伤效应和防护效果造成重要影响. 虽然具有一定置信度的数值模拟能够在免实验情况下得到该圆柱空爆近场超压流场，但是为了对其影响进行快速响应评估，需要进一步研究圆柱装药情况下近场空间超压的快速估算方法.

2 圆柱装药炸药空爆的近场超压估算公式

由于近场超压的实验数据点严重不足，难以通过已有实验数据的拟合给出具有一定置信度的近场空间超压估算方法. 考虑到模拟结果可以提供拟合所需的充足的三维空间样本数据，本节以经过初步校验的模拟结果作为样本空间来拟合近场超压的估算公式，并给出其在6 个不同长径比下的实验验证.

在无率效应的流体模拟中，相同长径比、不同质量圆柱装药的模拟结果存在缩比相似性. 以上节10 kg装药TNT 空爆模拟得到的近场超压数据(图2(a)～图2(c))为基础，在圆柱长径比 1/4 ≤L/D≤4范围内进行内插，可近似得到 1/4 ≤L/D≤4范围内某个长径比下近场空间内某一位置上的超压. 将内插函数记为Pover(L/D,R¯,θ)，该插值函数即为基于模拟结果拟合的圆柱装药空爆近场空间超压估算公式. 该超压估算公式含有圆柱长径比L/D、等效衰减距离R¯与空间角度 θ三个自变量. 由于模拟得到的样本空间内基础数据采样点较多，该函数拟合难度较大、且不唯一.本文拟合过程的具体做法分为三步.

①将图2 中不同长径比、不同角度上具有相同等效衰减距离的超压进行平均. 以Henrych 公式的形式对该超压平均值进行拟合，可以得到1/4 ≤L/D≤4范围内平均压力仅随等效距离R¯变 化的Pover(R¯)形式

2.1 近场超压估算公式的拟合过程

需要注意的是，为了适应近场较高的超压，估算式(8)是以MPa 为单位的，而Henrych 式(2)是以0.1 MPa 为单位的. 作为采样空间的内插函数，式(8)的适用范围显然是受内插空间内基础数据可靠性限制的. 本文在第2 节通过实验验证了模拟数据的在一定范围内的可靠性，可初步认为式(8)的适用范围为1/4 ≤L/D≤4,0.2 ≤R¯ ≤2.0. 下面仍需对估算公式在适用范围内的可靠性进行实验验证.

2.2 近场超压估算公式的实验验证

图7 给出了在长径比L/D≈1/4,1,4与等效衰减距离R¯ ≈1.3,2.0位置上圆柱空爆近场超压估算公式与实验结果[19]的对比. 图7 中的实验数据点为Pentolite 炸药等效TNT 炸药超压，与图3、图4 中的给出的实验结果相同，仅将图3、图4 中红色线标识的模拟结果替换为用蓝色线标识的估算公式曲线. 由图7 对比看到，估算公式与实验结果在近场空间中不同角度上的超压变化趋势符合较好. 由于估算公式使用二次多项式形式拟合，个别角度上仍然存在一定的误差. 除个别角度外，圆柱炸药空爆近场超压估算公式结果与实验点均值误差在60%以内，略大于模拟结果与实验均值间的最大误差值（45%）.

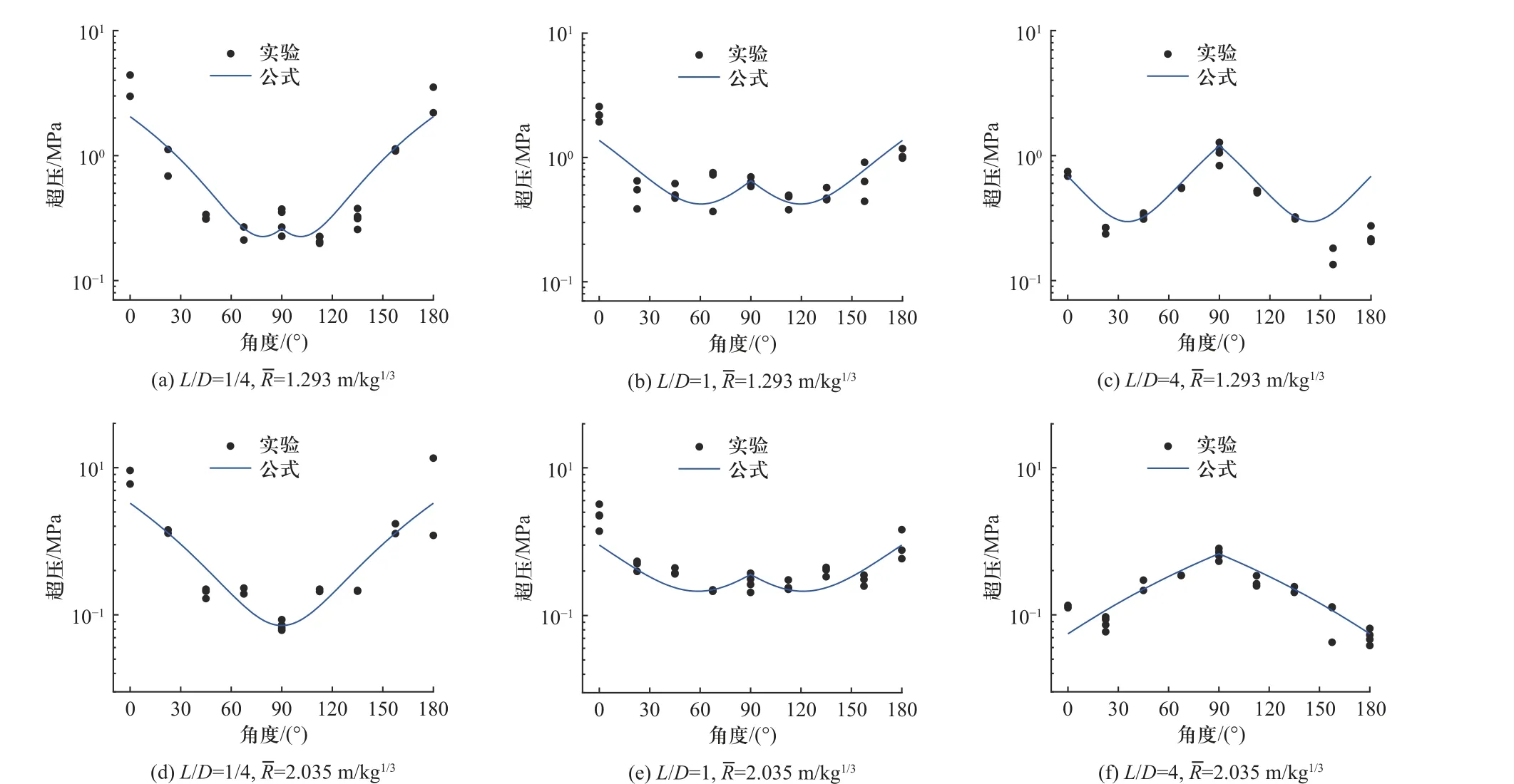
图7 圆柱空爆近场超压估算公式与三个长径比下的实验结果的对比Fig. 7 Comparison between the overpressure estimation equation of cylindrical air blast and the experimental results under three length-diameter ratios

实际上，图7 的对比仅校验表3 中给出的三个长径比下的拟合参数，在长径比变化情况下估算公式(8)中线性内插的合理性未能得到校验. 下面通过与实验结果对比对估算公式在内插空间的置信度进行初步验证. 图8 给出了长径比L/D=1/2,2,3 与等效衰减距离R¯ ≈1.3,2.0位置上圆柱空爆近场超压估算公式与实验结果的对比. 遗憾的是，该组实验仅给出了0°、45°、90°、135°、180° 5 个角度的超压结果，且重复实验数较少（参见文献[19]中的表3）. 由图8 对比看到，除个别角度外，估算公式结果与实验均值最大误差约65%（图8(a)中的90°角位置点），与图7 中最大误差基本相同. 经实验验证其在长径比范围1/4 ≤L/D≤4内插的可靠性得到了初步校验.

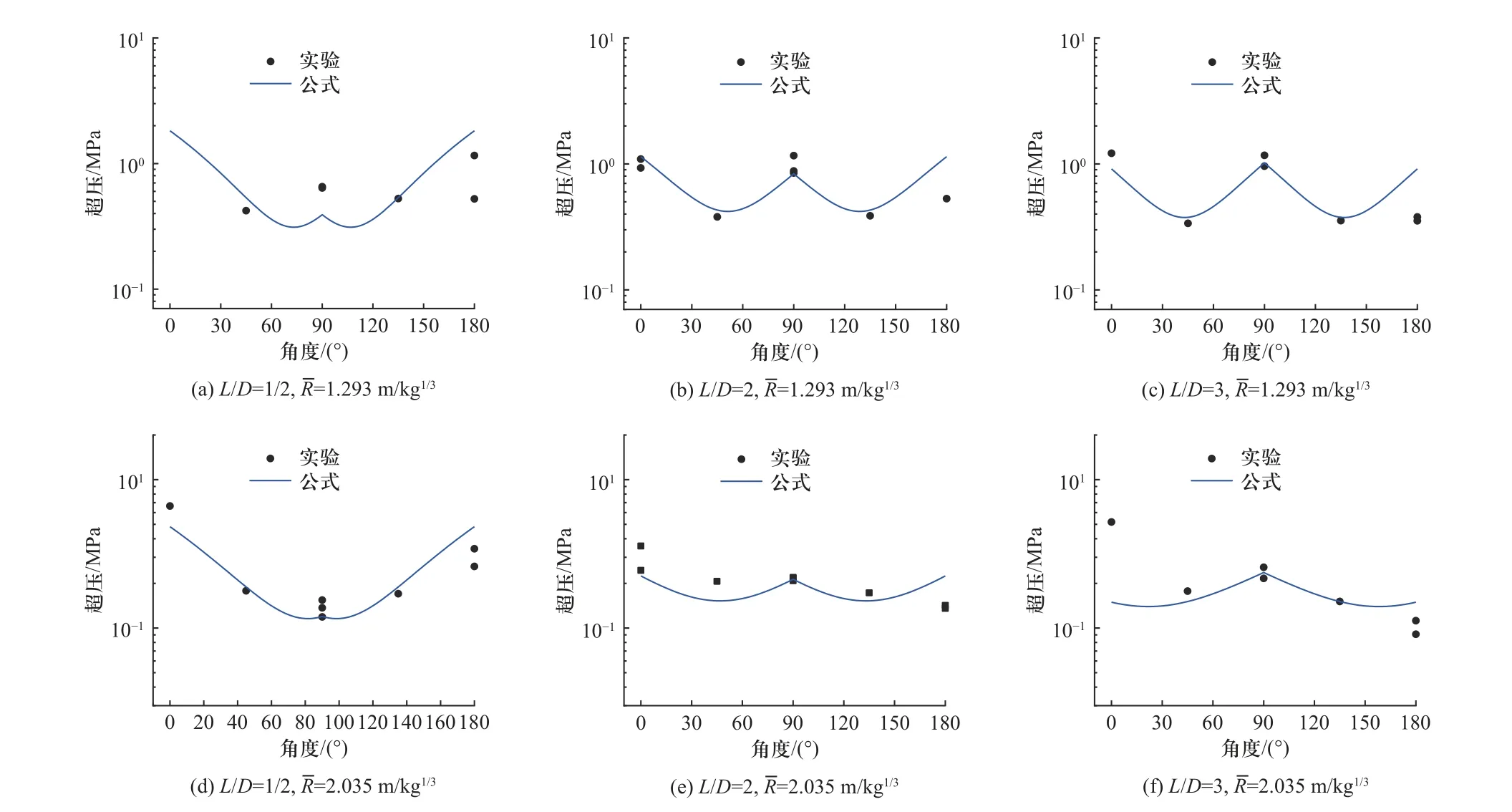
图8 在内插情况下的超压估算公式与实验结果的对比Fig. 8 Comparison between the overpressure estimation equation with experimental results in the case of the interpolation of length-diameter ratios

较使用球形装药空爆超压公式给出的不区分不同角度上超压差异的结果而言，圆柱装药超压估算公式在近场的超压误差较小，能够半定量体现圆柱空爆所引起的近场空间不同位置上的超压变化. 由于没有更多长径比情况下的实验数据进行验证，目前无法判断估算公式(8)在长径比外延(L/D＞4或L/D＜1/4)情况下的可靠性. 近场超压估算公式(8)的适用范围的进一步验证和拓展仍然需要大量实验支撑.

3 结 论

圆柱形炸药空爆后在近场空间存在复杂波系相互作用和极度不均匀的超压流场，此时若应用传统不区分不同空间角度上超压差异的球形装药超压经验公式则会引入较大误差. 针对圆柱炸药空爆近场空间超压流场的研究，在纯理论和实验研究较为困难的情况下，以经过实验校验的模拟结果作为样本空间拟合给出了圆柱炸药空爆的近场超压估算公式. 经过初步实验校验，其适用范围是1/4 ≤L/D≤4,0.2 ≤R¯ ≤2.0. 估算公式能够以免模拟、免实验的形式在相对较小的误差下给出圆柱炸药空爆后在近场空间任意位置上的超压. 本文研究是对传统球形装药经验公式的有益补充，可应用于圆柱装药空爆在近场空间毁伤效应和防护效果的快速评估.

仍需说明的是：若炸药种类、初始气压等发生变化，则需在作相应等效后才可应用本文估算公式；若圆柱起爆方式非体心一点起爆则会影响估算公式在0°与180°附近超压的准确性，此时需要对特定区域的超压进行修正；由于空爆近场波系在多次聚心反射作用后不是简单的类三角波（存在多个波峰），圆柱炸药空爆近场冲量变化的研究将更为复杂. 针对上述问题我们也将开展进一步的深入研究，从而进一步提高圆柱空爆近场估算模型的准确性和适用性.