近自由面水下爆炸气泡与破损结构耦合作用机理研究
张之凡,谢宇杰,王成,邓万超,廖全蜜
(1. 大连理工大学 船舶工程学院, 辽宁, 大连 116024;2. 北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;3. 深圳信息职业技术学院, 广东, 深圳 518172)
随着舰船防护性能的提高,鱼雷等传统水中兵器难以在一次毁伤后使舰船丧失战斗力,二次和多次 毁 伤 已 成 为 海 上 作 战 必 须 采 取 的 手 段[1-3]. 与 首 次毁伤时不同,二次毁伤时水下爆炸气泡将与破损结构发生相互作用,此时气泡的脉动特性和射流形态与完整结构相比差异较大,自由面和破损结构的双重边界条件将提高问题的复杂性.
国内外对近自由面气泡动态特性的研究起步较早,在理论分析方面,KLASEBOEI 等[4]提出了改进的RP 方程,计及重力和表面张力的影响,分析了气泡在刚性壁面和自由面附近的非球状运动过程,总结了相关的气泡运动规律. 李健等[5]在可压缩流体非保守系统中建立运动微分方程,讨论了气泡运动的脉动气泡半径、膨胀速度、加速度、气泡中心点位移、上浮速度、加速度等相关特性. 在实验研究方面,崔璞等[6]采用小当量PETN 开展水下爆炸实验,利用高速摄像机捕捉了近自由面水下爆炸气泡的形态.SUPPONEN 等[7]使用激光在近自由面处产生气泡,研究了近自由面气泡运动特性. 张阿漫等[8]采用电火花技术生成气泡,开展了多种边界条件下气泡动态特性的实验研究,系统地分析了不同边界条件下气泡的作用机理和运动特性. 在数值模拟方面,那立民等[9]基于LS-DYNA 软件的ALE 算法对近自由面水下爆炸的演化特征进行了研究,发现了爆距比与水冢形态的参数化关系. XU 等[10]采用欧拉有限元法对可变形海床和自由面之间的水下爆炸进行了数值研究,发现了可变形海床对气泡具有显著的影响. 综上所述,前人的研究大多局限于自由面影响下气泡的运动特性,针对自由面与结构耦合边界下水下爆炸气泡动态特性的研究尚不充分.
许多学者也进行了气泡与破损结构相互作用的研究工作. DADVAND 等[11]结合电火花气泡法和边界积分法研究了气泡在带圆形破口的背水平板附近的运动规律,发现气泡产生朝向或者远离破口的气泡射流取决于破口尺寸. 黎一锴等[12]针对刚性圆柱附近水下爆炸气泡的动力学特性进行了研究. 基于Navier-Stokes 方程结合流体体积法捕捉气液两相界面,建立了数值模型,发现了随着距离参数的增大,射流冲击压力逐渐减小,气泡内部最大射流速度先增大后减小,气泡型心的偏移随距离参数的增加而减小. 贺铭等[13]分析了气泡与水面双层破口结构的相互作用,总结了破口尺寸、起爆位置和壳间水位对气泡动态特性的影响规律. 张昌锁等[14]基于Autodyn 对近带孔刚性壁气泡脉动及水射流现象进行模拟,发现减小破孔半径对于破孔射流起增益作用,增大爆距对壁面射流起减益作用. 崔璞等[15]采用电火花气泡实验方法研究了带圆孔毗部附近的气泡动态特性,探究了7 种典型工况,发现了气泡行为高度依赖于破口距离参数和破口直径参数. 王诗平等[16]研究发现平板破口的存在会使得气泡发生靠近破口一侧的“腔吸现象”,并使气泡形成对向射流. 前人对于气泡与破损结构相互作用的研究主要局限于自由场或平板结构附近,对于浅水条件下自由液面、破损结构与水下爆炸气泡的耦合作用机理研究尚不充分.
在破损结构与自由液面的共同作用下,气-液-固三相耦合将使得气泡的运动规律和射流特征变得更加复杂,也难以预测. 本文针对这一问题,采用商业有限元软件Abaqus 的耦合欧拉-拉格朗日(CEL)方法,研究了近自由面条件下水下爆炸气泡在破损结构附近的动态特性. 首先,建立近自由面水下爆炸模型,将仿真结果与实验数据对比验证方法的有效性. 随后,对比分析有/无完整直角固壁结构附近的近自由面气泡动态特性. 最后,分析近自由面带圆形破口的直角固壁结构附近的气泡动态特性,并进一步讨论破口大小对倾斜射流几何参数的影响规律. 研究结果能够为舰船抗爆抗冲击研究提供理论基础与数值支撑.
1 基本理论
1.1 控制方程
在CEL 方法中,拉格朗日单元的节点随物质点同步移动,而欧拉单元的节点在空间中固定不动. 拉格朗日单元可以在欧拉网格内变形和运动,并且与含有材料的欧拉单元发生耦合,流体网格对结构网格施加压力,结构网格则限制流体材料的流动. CEL方法兼有拉格朗日方法与欧拉方法的优点,在求解水下爆炸问题时具有独特的优势[17].
连续方程、动量方程和能量方程[18]形式为


1.2 状态方程
1.2.1 炸药状态方程
本文采用的炸药是PETN,爆轰产物采用JWL[18]状态方程描述:


表1 PETN 的JWL 状态方程参数[19]Tab. 1 Parameters of JWL equation of state of PETN[19]
1.2.2 空气的状态方程


表2 空气的状态方程参数[19]Tab. 2 Parameters of equation of state of air[19]
1.2.3 水的状态方程


水的状态方程参数如表3 所示.

表3 水的状态方程参数[19]Tab. 3 Parameters of equation of state of water[19]
2 近自由面水下爆炸气泡与结构耦合作用
2.1 数值验证与收敛性分析
为了验证CEL 方法处理水下爆炸气泡问题的准确性,本文根据4.0 g PETN 近自由面水下爆炸实验[6],建立了三维近自由面水下爆炸模型,欧拉域长×宽×高为2 m×2 m×4 m,水域深1.8 m,为了观察水冢现象,在水面上方设置2.2 m 的空气域,炸药选用PETN,药量为4 g,炸药设置在距水面0.13 m 处. 欧拉域的边界条件为流出无反射和限制流入流出.
图1 为近自由面水下爆炸数值仿真结果与实验[6]结果的对比,从图中可以看出,仿真结果的气泡动态与实验结果相比一致性较好,无论是初期的气泡膨胀,还是后期射流的形成和演化,均与实验较为接近. 气泡半径时间历程曲线对比结果显示,在t=19.5 ms 时,仿真结果气泡半径接近最大值Rmax=0.268 m;实验结果表明,气泡在t=20.5 ms 左右达到最大半径0.282 m. 最大半径及相应时刻的误差分别为4.8%和4.9%,证明了CEL 方法在模拟近自由面水下爆炸气泡过程的可靠性和准确性.

图1 近自由面水下爆炸实验[4]与仿真气泡半径与形态对比Fig. 1 Experimental [4] and numerical results of radius and shape of near free surface underwater explosion bubbles
网格密度对数值仿真的准确性和计算效率都具有很大的影响,因此在保证计算精度的前提下,确定合适的网格尺寸对数值仿真的顺利进行十分重要.本文选取完整结构近自由面水下爆炸工况,针对典型时刻t=18.0 ms 时不对称梨形气泡的横向宽度进行收敛性分析,不同网格数量下的气泡半径如表4 所示. 结果表明随着网格数量的增加,横向宽度趋于收敛,稳定在53.2 cm 左右,证明在网格数量1 504 000时,可以有效模拟结构附近的近自由面水下爆炸气泡动态特性,文章涉及到的水下爆炸气泡计算,欧拉域均采用这一网格尺寸.

表4 t =18.0 ms 时不同网格数量下的气泡宽度Tab. 4 Bubble width under different grid numbers at 18.0 ms
2.2 数值模型及工况设置
为了研究破损结构附近的近自由面水下爆炸气泡动态特性,本文在近自由面模型的基础上,加入直角形结构,采用刚体建模,结构内侧为空气,以此模拟舰船舷侧受到水下攻击的情景. 计算模型如图2所示,直角形结构两边长各0.7 m,与 PETN 的水平距离为0.3 m,结构距离与气泡半径的量纲一化参数为1.063,结构底部与PETN 的垂直距离为0.15 m,圆形破口中心与PETN 炸药中心位于同一深度,自由液面距离与气泡半径的量纲一化参数为0.532. 为了研究破口大小对气泡动态特性的影响,保持结构与自由液面边界的距离参数不变,改变破口大小. 计算的工况如表5 所示:工况1 为近自由面爆炸,验证计算方法的可靠性;工况2 在近自由面的基础上引入了完整结构,探究完整机构附近的气泡动态特性;工况3~13 在完整结构上加入破口,通过调整破口大小,探究破口尺寸对气泡动态的影响.
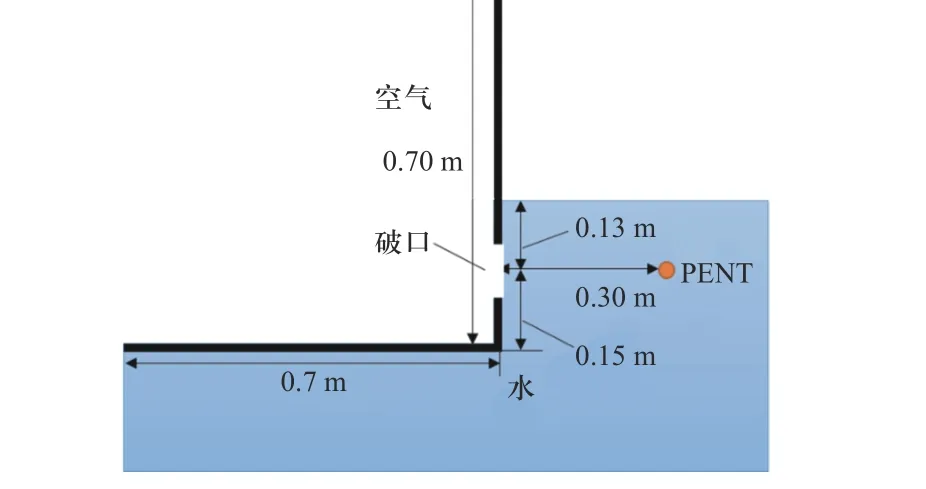
图2 结构附近的近自由面水下爆炸数值模型Fig. 2 Numerical model of structure subjected to near free surface underwater explosion
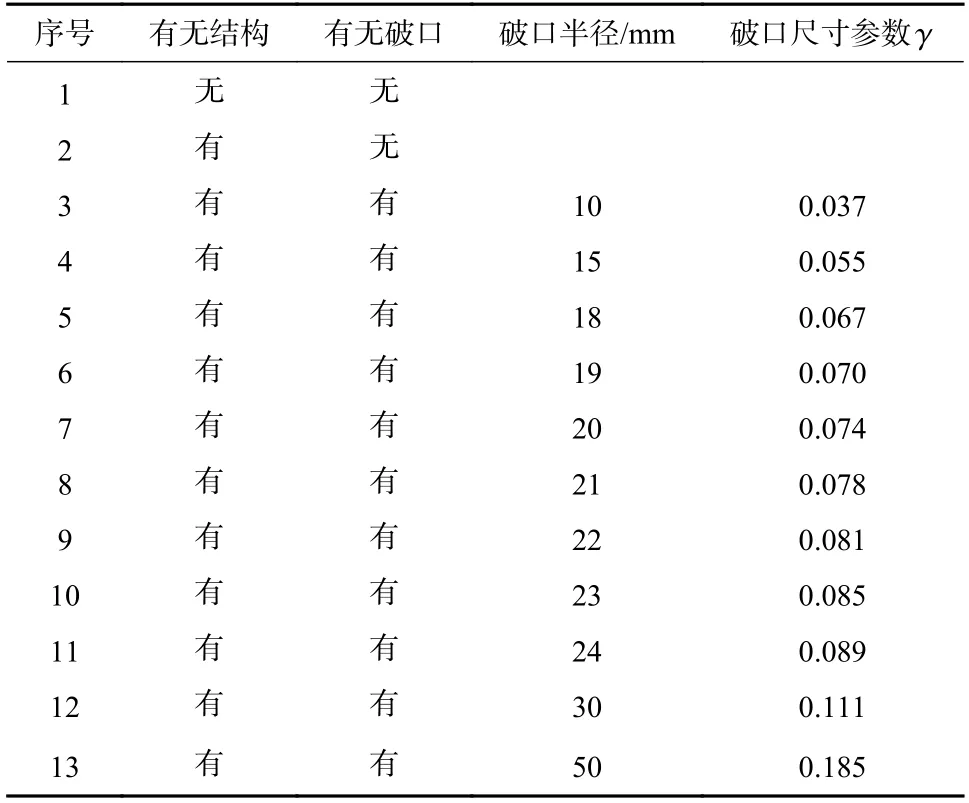
表5 仿真工况及参数Tab. 5 Cases and parameters
为了探究破损结构附近的近自由面气泡特性,本文设计了不同破口尺寸的工况进行研究,定义量纲一化破口尺寸参数如下:

式中:W为炸药TNT 当量;h为炸药深度.
2.3 完整结构附近气泡动态特性
为了分析结构对近自由面气泡动态特性的影响,图3 和图4 为典型时刻下近自由面完整结构附近与无结构工况水下爆炸气泡动态变化过程的数值仿真结果对比. 由于结构附近的气泡呈现非球状,采用气泡横向最大宽度的1/2 作为等效半径. 结果显示在气泡膨胀的初期,结构对气泡的影响有限,两种工况下气泡动态变化和气泡半径的差别很小. 随着气泡的膨胀,气泡边界与结构的相互作用加剧,气泡左侧受到结构的影响,t=8.0 ms 时气泡呈现不对称的梨形.t=13.0 ms 时两个工况下气泡顶端都出现凹陷,开始形成向下射流,表明结构并未影响射流的产生.t=19.5 ms 时两个工况下气泡均膨胀至最大,双重边界条件下气泡的最大半径略小于近自由面附近气泡的最大半径. 随后气泡开始收缩,t=21.5 ms 时由于结构的吸引和水冢的压迫,与无结构工况下的球形气泡不同,左上部分气泡呈现直角形状,此外,向下的射流呈现明显的偏折现象. 由于收缩过程初期气泡的内部压力小于外界流体,左侧流场受到结构的限制,在大气压和重力的作用下,水冢底部左侧在t=21.5 ms 时由于失去支撑发生凹陷,并在后续过程中演化加剧,水冢顶部发生弯曲.t=25.0 ms 时两个工况射流头部同时到达气泡下边界,气泡底部开始凸起,形成双连通域.t=30.5 ms 时在偏折射流、壁面的吸引以及水冢底部左侧凹陷的共同作用下,双重边界下的气泡呈倾斜状,底部凸起在偏折射流的影响下开始破碎,同时气泡继续收缩,气泡行为较之自由液面单边界工况下变得更加复杂.
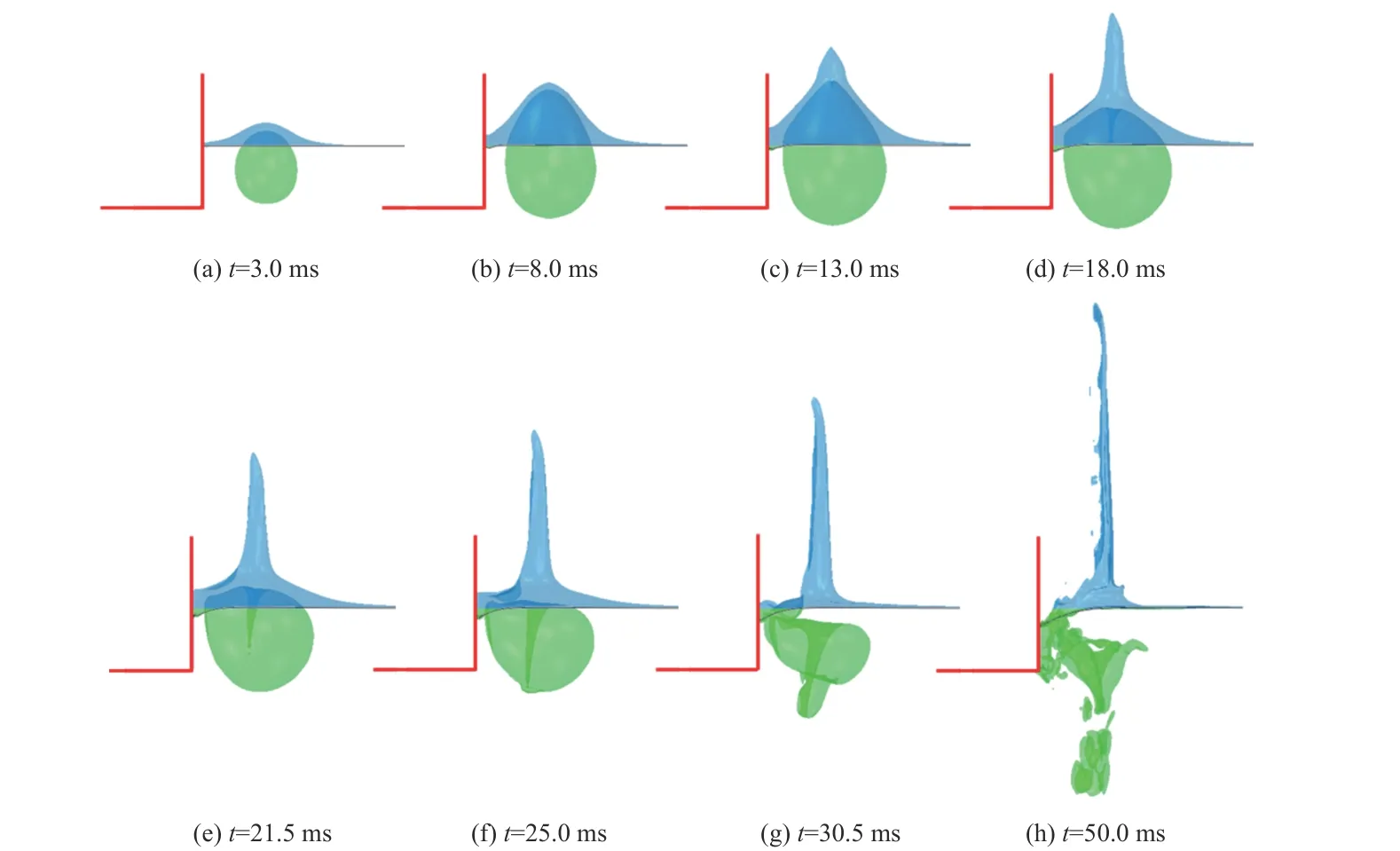
图3 完整结构工况气泡动态Fig. 3 Bubble dynamics near complete structure
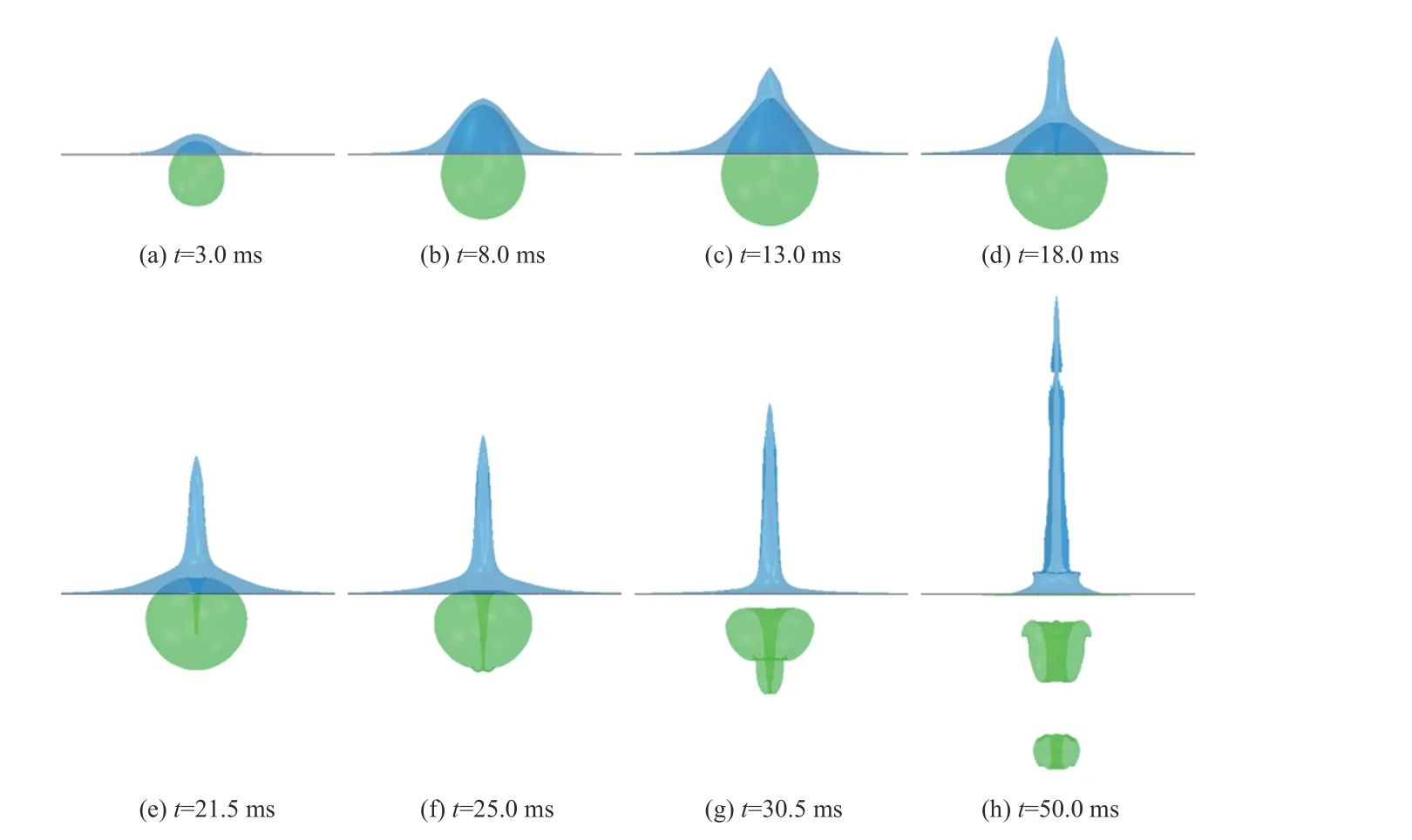
图4 无结构工况气泡动态Fig. 4 Bubble dynamics near free surface without structure
为了进一步分析结构对近自由面气泡动态特性的影响,图5 给出了完整结构工况与近自由面工况下气泡半径随时间的变化曲线,由图可知,近自由面和双边界条件下气泡的最大半径分别约为0.268 m和0.254 m,这表明结构的存在影响了气泡膨胀过程中的半径大小,但对脉动半周期的影响较小,完整结构的存在限制了气泡的膨胀,使得气泡最大半径略小于近自由面单边界工况,并且由于后期气泡倾斜和偏折射流等现象的影响,气泡趋于破碎,气泡半径已无法测量.
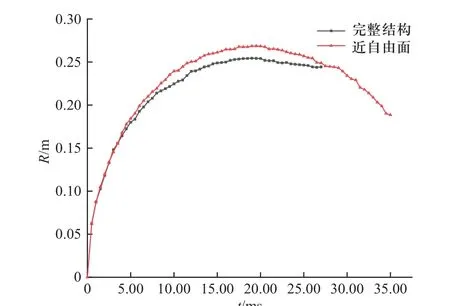
图5 完整结构工况与近自由面工况半径时历曲线对比Fig. 5 Comparison results of evolution of bubble radius near free surface with and without structures
2.4 破损结构附近气泡动态特性
本节在完整结构工况的基础上,保持炸药与结构的相对位置不变,圆形破口中心与炸药位于同一深度,本节将探究破口大小对破损结构附近的近自由面气泡动态特性的影响.
图6 为破口半径参数γ=0.078 工况下典型时刻气泡动态变化过程,与完整结构工况相比,气泡在结构一侧产生了明显的指向气泡内部的倾斜射流. 从图中还可以看出,在气泡膨胀初期,t=3.0 ms 时破口处受到冲击波和气泡挤压的影响产生了涌流. 气泡在初期呈现与完整结构工况相同的不对称梨形,并且未影响13.0 ms 时形成的向下射流的形态,该工况下同样捕捉到了向下射流的偏折、气泡整体倾斜以及水冢一侧底部凹陷等现象;与完整结构工况不同的是,t=15.0 ms 时,气泡在结构一侧发生向内凹陷,逐步产生向内的射流,射流尾部略低于破口中心,射流尾部宽度大小为101 mm,头部射流宽度为43 mm;t=24.5 ms 时,倾斜向上射流与向下射流交汇,阻止了倾斜射流的进一步发展,再加上此时气泡的收缩,多种现象的联合作用使得气泡在t=30.5 ms 时趋于破碎,早于完整结构工况下气泡的破碎时间.

图6 21 mm 破口下气泡的动态变化过程Fig. 6 Bubble dynamics near structure with hole of 21 mm
2.5 破口半径对射流的影响规律
2.5.1 倾斜射流产生的破口尺寸区间
水下武器攻击舰船后,造成的破口并不一致,为了研究破口半径对射流产生及形态的影响规律,本文调整破口尺寸参数γ,对带破口结构附近气泡的动态特性进行模拟,探究破口大小对倾斜射流的影响.图7 为不同破口尺寸工况在t=23.0 ms 典型时刻时的气泡动态,计算结果汇总于图8. 由图可知,破口尺寸的改变对水冢高度和气泡整体形态的影响很小,破口尺寸主要影响了倾斜射流的形态. 当破口尺寸参数γ位于0.070~0.085 区间内,气泡会在靠近结构一侧产生倾斜射流,其余工况下,破口的影响不足以使其产生射流,但均有不同程度的凹陷.
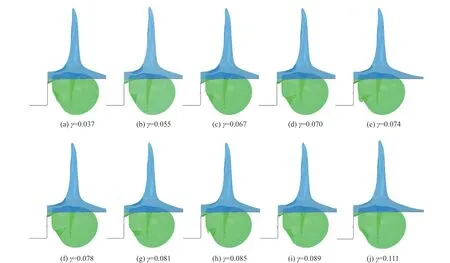
图7 t=23.0 ms 典型时刻时不同破口尺寸工况气泡动态Fig. 7 Bubble dynamics near structure with different hole sizes at t=23.0 ms
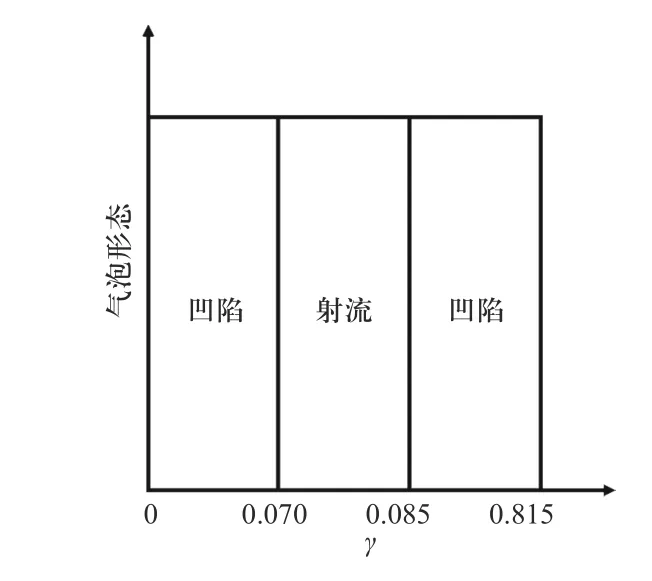
图8 气泡形态随破口尺寸参数γ 的变化Fig. 8 Variation of bubble shape with hole size parameter γ
2.5.2 破口尺寸参数γ对倾斜射流形态的影响
破口尺寸对于射流的尾部宽度、头部宽度和倾斜角度具有明显的影响. 射流角度是指射流中轴线与水平方向的夹角. 由于侧向的射流呈现不规则的柱形,因此对于射流的几何特性采用了射流的头部宽度和尾部宽度两个参数来描述. 射流头部宽度指的是射流向内凹陷的连续体内部的宽度,尾部宽度指射流向内凹陷开口处的宽度. 图9 所示为射流形态随γ的变化曲线. 在γ=0.074~0.085 区间内,随着破口的增大,射流头部逐渐变粗,由44.0 mm 逐渐增加至57.5 mm,可见破口的增大有利于射流头部的发展演化. 破口尺寸对射流尾部的影响趋势并不明确,在γ=0.074~0.085 时,射流尾部宽度均为123.2 mm,明显高于其他工况. 破口增大对射流角度的呈现出明显的正向影响,随着破口的增大,射流角度呈现曲折上升的趋势,从30.11°增加到了38.85°,差距明显,证明破口的增大总体上促进了射流向上倾斜.
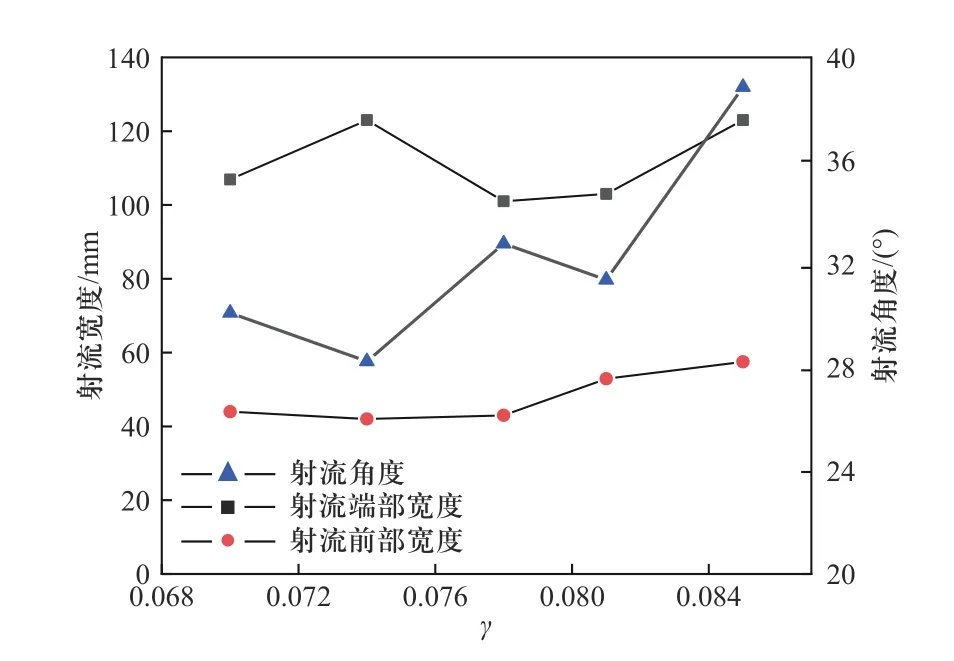
图9 射流形态随γ 的变化曲线Fig. 9 Variation curve of jet shape with γ
2.5.3 破口尺寸参数γ对倾斜射流头部速度的影响
随后分析破口尺寸对倾斜射流头部速度的影响,图10 为不同破口尺寸下射流头部速度时历曲线,记录了倾斜射流从产生到与向下射流交汇全过程的头部速度变化情况. 由图可知,破口尺寸对射流产生时间和相遇时间的影响较小,不同破口尺寸下,射流均在15.0 ms 左右产生,并在24.5 ms 左右与向下发展的射流发生交汇. 在不同的破口尺寸下,倾斜射流的头部速度随时间的变化趋势一致,均呈现出先增大,而后保持一段时间的“平台期”,最后速度急剧下降的过程. 但不同破口尺寸工况下,平台期的速度有所不同,图11 为不同破口尺寸γ下射流平台期速度均值与持续时间,在破口尺寸参数γ<0.081 的区间内,随着γ增大,倾斜射流的平台期头部速度增大.γ=0.081 工况下,射流平台期速度最大,保持在21.42 m/s左右,γ=0.074 和γ=0.085 两个工况的平台期速度最小,保 持 在16.42 m/s 左 右. 从 不 同 破 口 尺 寸γ下 射 流 平台期续时间可以看出,γ=0.078 工况下的射流平台期持续时间最长,射流最为明显.

图10 不同破口尺寸γ 下射流头部速度时历曲线Fig. 10 Evolution of jet-head velocity near structure with different hole sizes of γ

图11 不同破口尺寸γ 下射流平台期速度均值与持续时间Fig. 11 Average velocity and duration of bubble jet during platform phase with different hole sizes γ
3 结 论
本文基于CEL 方法,首先建立近自由面水下爆炸模型,将仿真结果与实验数据进行验证验证数值模型和计算方法的可靠性,随后对比分析了在结构距离参数为1.063,自由液面距离参数为0.532 的典型工况下,完整和破损结构附近自由面水下爆炸气泡的动态特性,最后讨论了破口尺寸对气泡倾斜射流产生及形态的影响规律. 结论总结如下:
①采用CEL 方法能够有效模拟近自由面水下爆炸过程,气泡周期、形态等仿真结果与实验吻合良好. 通过对比分析有/无结构时近自由面气泡动态特性发现,结构的存在影响了气泡膨胀过程中的半径大小,但对脉动半周期的影响较小,且并未影响向下射流的形成,但结构与自由面的共同作用会使得气泡出现整体倾斜,向下的射流发生偏折,水冢一侧凹陷和后期气泡破碎等现象.
②对比分析完整和破损结构附近气泡动态特性结果显示,破损结构可使近自由面气泡在靠近结构一侧产生向内的倾斜射流,本文的典型工况下,当破口半径处于0.070~0.085 倍气泡最大半径时,破口的存在可以产生倾斜射流,其他工况下气泡仅产生不同程度的凹陷.
③破口尺寸对于倾斜射流的尾部宽度、头部宽度和倾斜角度具有明显的影响,其中,破口尺寸的增大对射流的头部宽度和倾斜角度呈现明显的正向影响,总体上促进了射流向上倾斜,但对射流尾部宽度的影响趋势并不明确.
④不同的破口尺寸下倾斜射流头部速度随时间的变化趋势较一致,均呈现出先增大而后保持平稳最终急剧下降的趋势;随着破口尺寸参数γ的增大,倾斜射流的平台期头部速度增大;γ=0.078 工况下的射流平台期持续时间最长,射流最为明显.

