斜坡堤新型人工块体TB-CUBE的波浪爬高和反射试验研究*

彭 程，王 昊，娄雅冬，褚逸云，陈松贵

(1.交通运输部天津水运工程科学研究院 港口水工建筑技术国家工程实验室，天津 300456；2.港口水工建筑技术国家工程研究中心，天津 300456；3.中交第一航务工程局有限公司，天津 300456；4.河海大学 港口海岸与近海工程学院，南京 210098)

波浪在向岸传播过程中到达斜坡式水工建筑物时，水体沿斜坡堤上爬高程与静水面高程之差称为波浪爬高。在工程设计中，一般以波浪爬高确定建筑物的堤顶高程，以防止越浪[1]对堤后造成破坏。因面临强风浪等自然条件的破坏作用[2-3]，工程设计上常采用人工护面块体[4]斜坡堤来保护堤后建筑物。目前，国内外开发的人工块体根据其形状和构造通常分为3种类型：杆件形结构、空心形结构、实心形结构。杆件式块体依靠护面层之间的空隙和块体表面粗糙度形成的紊流消能；空心式块体主要依靠水体进入块体内部形成的紊流消能；实心式块体则通过块体间空隙和表面凸起物起到消能作用。

对于一种新型护面块体的水动力特征，研究其爬高特性、总结其爬高经验公式具有重要的意义。国内外学者对于爬高的试验研究比较全面，并总结出各种类型块体的爬高公式。对于单坡的爬高计算方法，Ahrens[5]根据相关物理模型试验资料，计算出了波浪在光滑不透水板上的理论爬高。我国目前单坡爬高的相关公式主要依据规范[6-8]。濮勋等[9]认为《堤防工程设计规范》与《港口与航道水文规范》中的波浪爬高计算公式的计算值总体上比较接近，但是前者的计算结果比后者要大一些。van der Meer[10]公式考虑了波高、周期、坡度对爬高的影响，更能接近爬高的真实规律，但其仅适用于坡度较缓的防波堤。欧美国家应用van der Meer[11]计算方法较多。卢永金等[12]认为按照《堤防工程设计规范》计算的波浪爬高值与van der Meer法乘以风影响系数计算的波浪爬高值结果基本相当，但2种计算方法在乘以影响系数时有较大区别，适用范围也不同。

美国学者Saville[13]根据众多学者研究成果，绘制了一套波浪爬高曲线图，该图被美国海岸防护手册(SPM)收录[14]。翁克勤[15]分别从波高、波向、堤前水深等角度对波浪爬高做了系统研究。张华[16]系统阐述了堤前水深对波浪爬高的影响机理，分析了影响波浪最大爬高的因素，并给出了相应的经验计算公式。陈国平等[17-18]通过物理模型试验，研究了不规则波作用下波浪在光滑不透水板上的波浪爬高，并且分析了波陡、坡度、波浪入射角、平台宽度和高程等主要影响因素对波浪爬高的影响规律，并与40多个实际工程的模型试验结果对比，具有较好的计算精度。朱嘉玲等[19]研究了不同入射方向的规则波对于斜坡堤波浪爬高的影响，通过相关试验提出了计算斜坡堤规则波作用下波浪爬高的修正公式。Kenji等[20]提出了一种新型的块体，兼具护面、消波、人工礁等多项功能，且制作成本低，能支持多种设施。Park等[21]介绍了一种新型混凝土块体Chi Block，该块体具有较高的稳定性和结构强度，可以用于护面修复。

防波堤结构形式和护面块体使用场景存在多样性，各爬高经验公式限制条件比较多，相关计算公式都是基于特定条件推导得出，并不能适用于所有护面块体，会导致各公式计算结果差异较大。对于一种新型块体，要想准确了解其爬高特性，可根据物理模型试验的数据推导其爬高经验公式。本文依托水槽试验，探究波浪在新型人工块体TB-CUBE上的爬高和堤前反射情况，拟合波浪在新型块体上爬高的经验公式，以了解其消浪特性。

1 试验概述

1.1 TB-CUBE块体简介

TB-CUBE块体由交通运输部天津水运工程科学研究院自主研发[22]，其消波原理主要是波浪在爬坡时从孔洞内进入块体与块体之间形成的消能室，形成漩涡、冲击和摩擦，耗散波浪能量，从而达到消波的目的。该块体具有孔隙率高、消浪效果好、安放适应性强、稳定性高、结构强度高等优点。TB-CUBE块体设计及实体见图1。

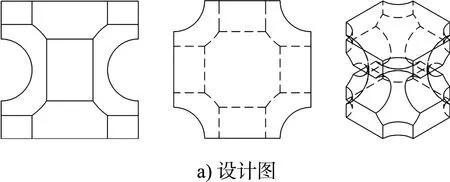
图1 TB-CUBE块体

1.2 试验设备

试验在交通运输部天津水运工程科学研究院风浪流试验水槽中进行，水槽尺寸为68 m×1.0 m×1.0 m(长×宽×高)。水槽一端安装有电机伺服驱动推板吸收式造波机，可产生规则波与不规则波。水槽两端均设有消波装置，同时水槽底部设有连通管，以使试验过程中模型两侧的水位保持不变。采用SG2008型高精度动态波高测量系统对试验波高进行采集和分析。

1.3 模型布置

模型几何比尺为1:40。模型断面为斜坡式结构，距离造波机32 m，为便于起波，将模型摆放在一个高0.20 m、坡度1:50的平台上。斜坡护面为TB-CUBE块体，块体质量为152 g。下设厚度为25 mm、质量为护面块体1/10～1/20的块石垫层。堤顶高程为0.65 m，预留一定高度以保证所有试验工况下不会发生越浪。试验中在堤前沿水槽中线共布置3个间隔0.50 m的波高传感器，序号沿波浪传播方向依次排列。模型布置见图2。

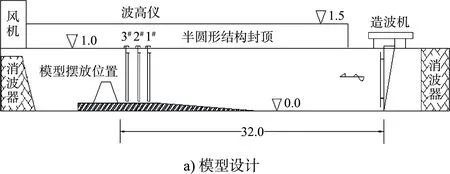
图2 模型布置(单位：m)

1.4 试验工况

从试验水深d、试验坡度m、波高H和周期T等4个角度进行研究分析。具体工况为：试验水深0.3、0.4 m，试验坡度(m=cotα，α为斜坡坡角)1.5、2.0、2.5，波高T0.06、0.08、0.10、0.12 m，周期1.2、1.5、1.8、2.2、2.5 s。

1.5 试验方法

1)波浪率定。依据《水运工程模拟试验技术规范》[23]，需在斜坡堤模型摆放前对每一组波浪进行率定。

2)数据采集与分析。进行试验时，忽略前4～5个不稳定波浪后进行采集，对于规则波连续采集的波浪个数至少20个，每组试验重复3次。数据处理时进行数据可信度的检查，去除异常数据，取3组平均值作为代表值。本次试验中，对于消波结构前的1#、2#波高传感器的数据，应用Goda两点法原理分离出消波结构前的入射波高和反射波高，计算消波结构的反射系数[24-25]。对于波浪爬高值采用电容式爬高仪测量，最大量程150 cm，仪器的灵敏度及稳定性均满足试验要求。

2 不同因素对波浪在新型人工块体上爬高的影响

2.1 斜坡坡度对爬高的影响

根据目前国内外研究资料，相对爬高(波浪爬高R与波高H之比，R/H)与坡度m之间的关系一般用裴什金公式或马克西姆楚克公式表达：

R/H=f(1/m)

(1)

R/H=f[1/(1+m2)0.5]

(2)

R/H-m曲线可以反映出不同波浪形态下波浪在斜坡堤上的爬高规律，见图3。根据试验结果可知：R/H-m曲线基本上呈现单峰，且波浪在块体上爬高随着斜坡堤坡度先增大后减小。

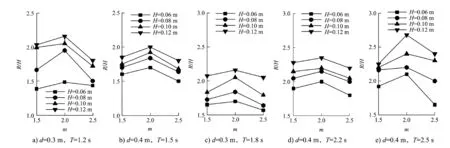
图3 不同波周期下相对爬高随坡度变化规律

当坡度m<2时，不同周期情况下R/H-m的变化规律基本一致，相对爬高随坡度的增大变化比较明显，以d=0.3 m、T=1.2 s、H=0.08 m为例，随着坡度从1.5增加到2.0，R/H从1.66增加到1.95；当坡度m>2时，相对爬高随着坡度的增加而逐渐减小，以d=0.3 m、T=1.2 s、H=0.08 m为例，随着坡度从2.0增至2.5，R/H从1.95减小到1.50。此外，在相同坡度情况下，波浪爬高随着波高的增加而增加，以d=0.3 m、T=1.2 s、m=2为例，H=0.06、0.08、0.10、0.12 m时，R/H分别为1.48、1.95、2.05和2.16。

2.2 水深对爬高的影响

当m=2时，不同波高情况下水深对波浪爬高的影响见图4。可以看出，波浪爬高随水深的变化规律为：随着相对水深(水深d与波长L之比，d/L)的增加，波浪爬高呈现先减小后增加的趋势。以H=0.06 m为例，当d/L<0.12时，随着相对水深从0.08增加到0.12，R/H从1.68减小到1.53；水体通过新型块体的孔洞进入块体内部的水流越来越多，块体内部水体的紊乱程度越来越大，块体对于水体的消浪效果越来越强。当d/L=0.12的时候，波浪在护面块体上的爬高值最小，说明此时块体对于波浪的消浪效果达到了最佳状态。当d/L>0.12时，随着相对水深从0.12增加到0.22，R/H从1.53增至1.90；随着水深的继续增加，爬坡水体层厚度也在逐渐增加，此时已经逐渐达到块体的极大消浪能力，块体对于水体层厚度消浪逐渐减弱，波浪在块体上的爬高又逐渐增加。同时，随着堤前波高逐渐增加，波浪在新型块体上的爬高也是逐渐增加的：以d=0.4 m、m=2、d/L=0.154为例，H=0.06、0.08、0.10、0.12 m时，R/H分别为1.75、1.94、1.99、2.22。

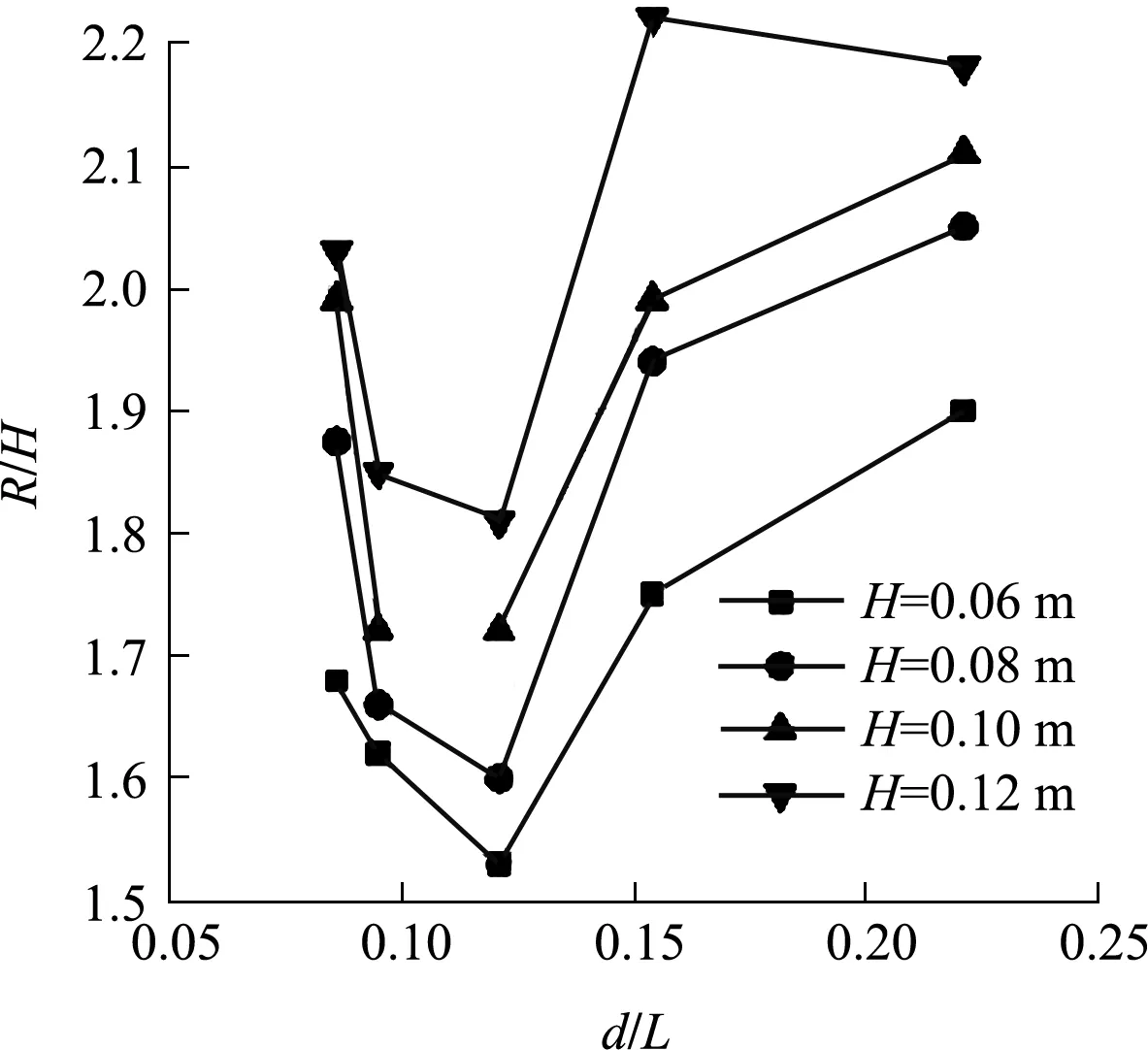
图4 m=2时波浪相对爬高随相对水深变化规律

3 不同因素对新型人工块体反射系数的影响

3.1 坡度对反射系数的影响

波浪的反射系数定义为：Kr=Hr/Hi，式中Hr、Hi分别为反射及入射波高。当d=0.3 m时，不同波高情况下斜坡坡度对反射系数的影响见图5。由图可知：在相同的入射波浪条件下，反射系数随着坡度的基本变化规律为：随着坡度的逐渐变大，堤前波浪的反射系数逐渐减小；以d=0.3 m、T=1.2 s、H=0.06 m为例，随着斜坡坡度从1.5增加至2.5，反射系数从0.31减小到0.18。说明随着坡度逐渐变缓，波浪在爬坡过程中沿程摩阻损耗以及块体内部的紊动耗能增大，使回流水体的能量减小，反射波的能量降低，最终表现为堤前反射系数减小。同时，在坡度相同的条件下，随着波高的增大，进入块体内部孔隙的波浪增多，新型人工块体的高孔隙率特征对进入孔隙的波浪有着良好的耗散效果，降低了堤前的反射现象，这说明该新型块体在面对较大波浪时可能更具优势。

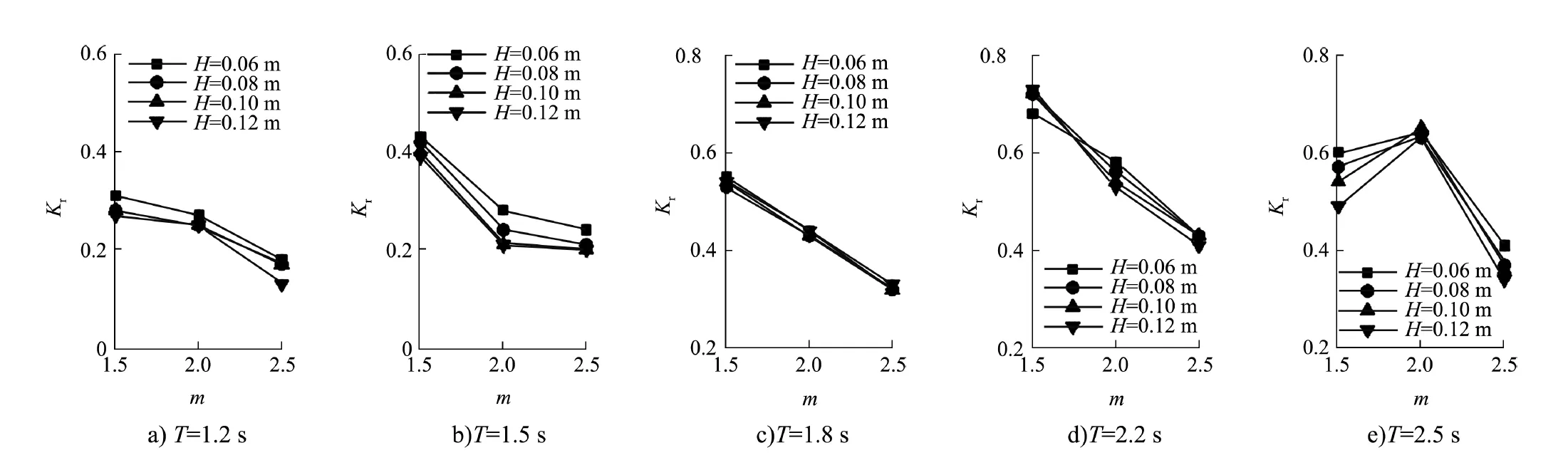
图5 不同周期下反射系数随坡度变化规律

值得注意的是，当T=2.5 s时，随着坡度的增加，反射系数呈现先增加后急剧减小的趋势，这说明波浪的反射率随坡度增大并非呈现单一减小的趋势。结合试验现象分析原因可能为：当周期和坡度达到某一关系值时，爬坡水体层会在块体表层形成一层薄水膜，使得进入块体内部孔隙波浪减少，块体内部耗散相对较小，回流水体仍具有较大能量，使得反射系数增加；当坡度继续增大时，水体在爬坡时形成的水膜现象消失，波浪在块体内部得以正常耗散，反射系数又急剧减小。

3.2 水深对反射系数的影响

图6为不同波高情况下堤前反射系数随相对水深的变化规律。从图中可以看出，水深对反射系数的基本影响规律为：随着水深的逐渐增加，堤前的波浪反射率逐渐减小；以H=0.06 m为例，随着相对水深从0.08增加到0.21，反射系数从0.63减小到0.28。

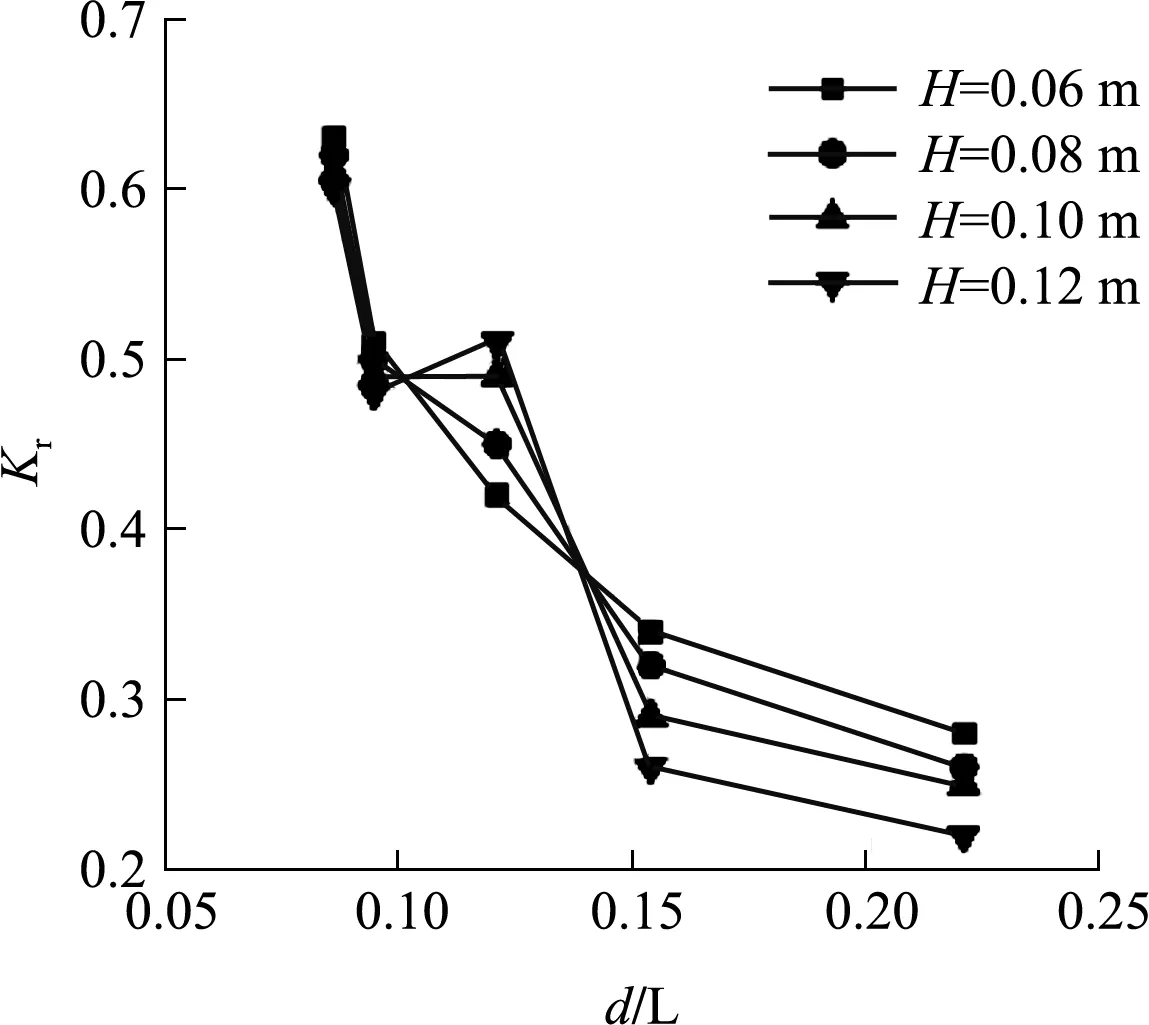
图6 堤前反射系数随相对水深变化规律

4 TB-CUBE块体波浪爬高经验公式拟合

本文前述主要分析了堤前水深、坡度等对新型人工块体波浪爬高的影响。在相同情况下，波浪在护面块体上的爬高主要受波高的影响。以d=0.3 m、m=1.5为例，不同周期条件下波高与爬高之间的关系见图7。可以看出，在其他条件相同时，波高与爬高基本成线性关系。

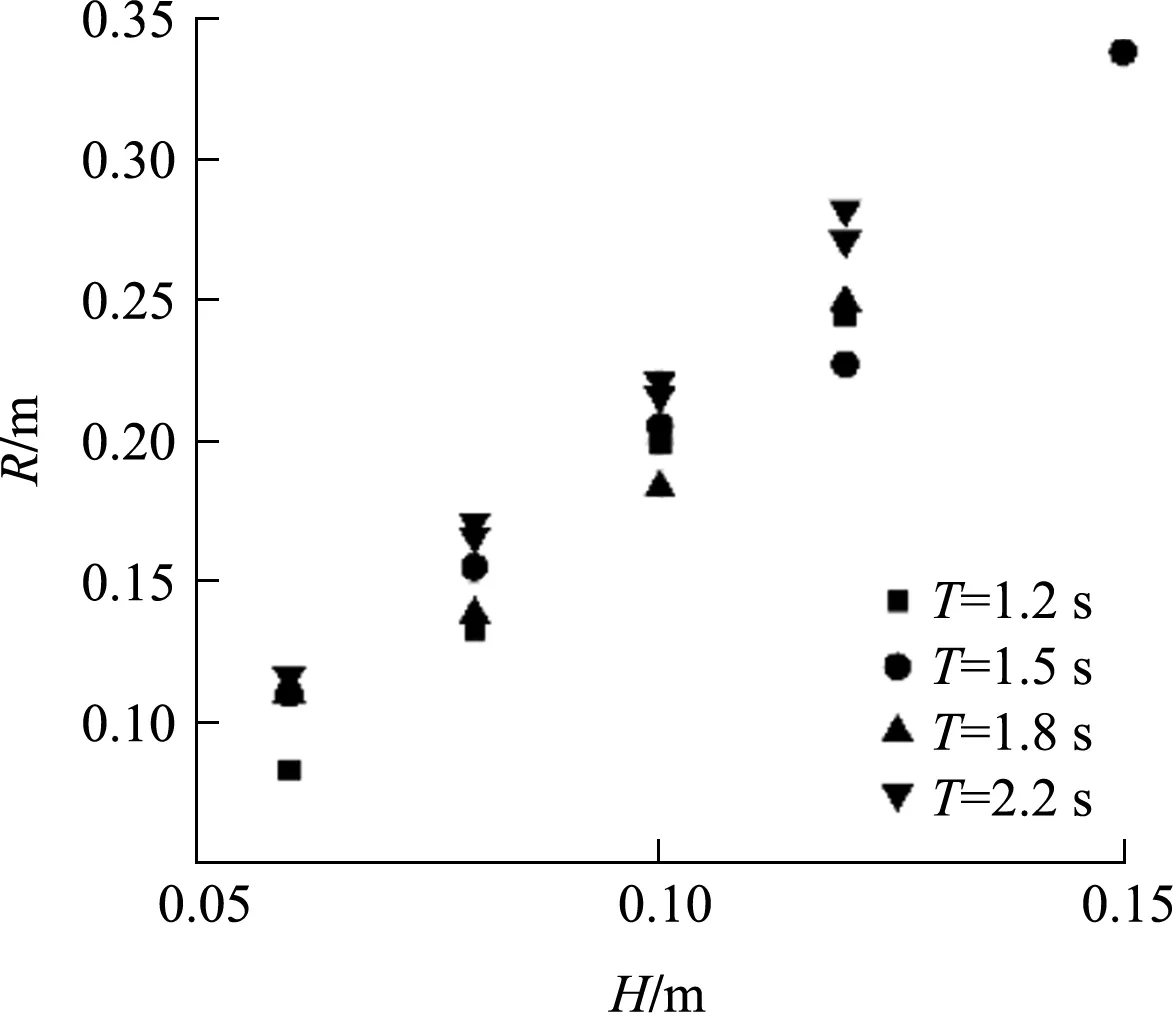
图7 不同周期下爬高随波高变化规律

经过数据分析，以相对爬高R/H和波坦L/d(波长L与水深d之比，即相对水深倒数)为参数，对不同坡度下的R/H与L/d之间的关系进行非线性拟合，以此来确值定斜坡堤不同坡度下对应的参数，拟合曲线见图8，其中函数A(m)、B(m)、C(m)的系数取值见表1。

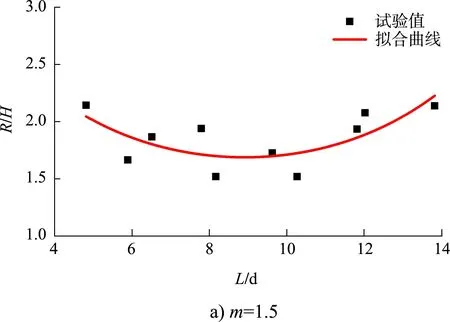
图8 不同坡度下拟合曲线

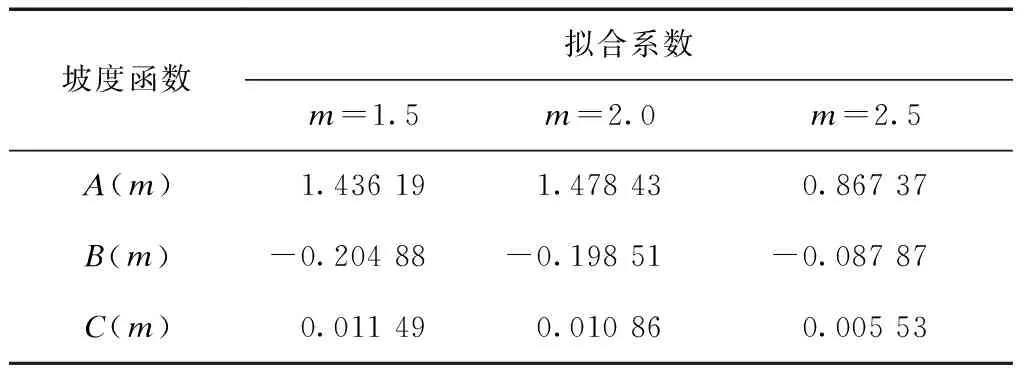
表1 拟合公式系数

把表1中不同坡度下的系数A(m)、B(m)、C(m)与坡度m值进行拟合，分析得到坡度函数与坡度之间的关系式。通过将各个公式进行拟合后，最终得到波浪在新型人工块体TB-CUBE上的爬高经验公式：

(3)

(4)

(5)

(6)

式中：R为波浪爬高值，从静水面计算，沿斜坡向上为正方向；L为斜坡堤堤前的波长；d为斜坡堤堤前水深；H为斜坡堤堤前平均波高；m为斜坡堤坡度。

为了分析拟合公式的精确度，分别采用该公式和JTS 145—2015《港口与航道水文规范》中正向规则波在斜坡式建筑物上的波浪爬高计算式与试验实测值进行对比分析。以m=2、d=0.3 m为例，拟合公式和规范计算式与实测值对比见图9。

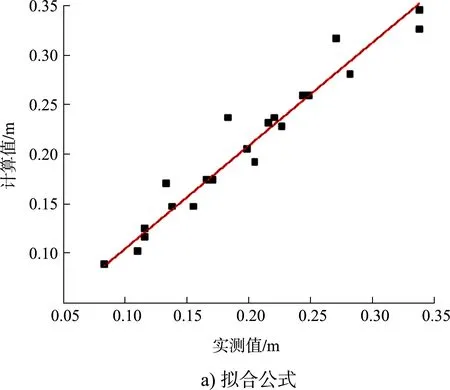
图9 拟合公式和规范公式与实测值对比

采用最小二乘法进行回归分析，得到拟合公式和规范公式相关系数值分别为0.994和0.948，即置信度分别为99.4%和94.8%；残差平方和分别为0.006 49和0.018 02。拟合公式值大于规范公式计算值且接近于1，残差平方和小于规范公式计算值。因此，在本次试验规则波作用下(相当于原型波高H变化范围为2.4～7.2 m，周期T变化范围为7.5～15.5 s)，该拟合公式的精确度高于规范公式，更适用于新型人工块体TB-CUBE上的爬高计算。

5 结论

1)斜坡坡度m由1.5增加至2.5时，新型人工块体TB-CUBE的波浪爬高随坡度增加呈现先增加后减小的趋势，R/H-m曲线基本上呈现单峰状态；

2)随着相对水深的增加，TB-CUBE块体的波浪爬高随坡度先减小后增加，当d/L=0.12时，R/H-m达到最小值；

3)随着斜坡坡度和水深的增加，TB-CUBE块体的波浪爬高和堤前反射系数均逐渐减小；

4)当波高增大时，堤前反射减小，进入块体内部孔隙的波浪增多，TB-CUBE块体的高孔隙率特征对进入孔隙的波浪有着良好的耗散效果；

5)通过量纲分析及多变量相关的方法获得规则波作用下TB-CUBE块体的爬高经验公式，并与国内规范计算式进行对比，拟合公式对该块体的适用性更高，可供该块体在堤防工程中的实际推广应用作为参考。