Lamb波多特征参数的复合材料损伤程度评估方法*

邱 文 王 强 孙大彪 胡伟伟 鲍 峤

(1 南京邮电大学自动化学院 南京 210023)

(2 南京邮电大学人工智能学院 南京 210023)

0 引言

复合材料由于具有高强度、重量轻、比模量大、低蠕动及强耐腐蚀性等优点，正逐步取代合金材料，广泛应用于航空航天、机械及土木工程等领域[1]。在复合材料的制造过程中，受制造工艺的影响，可能会引入原始缺陷，此外在服役过程中，受外部冲击、交变载荷等作用，结构内部会逐渐形成损伤。不同发展阶段下的复合材料结构损伤引起的结构材料参数变化不尽相同，对结构的力学性能会产生不同程度的作用和影响，因此针对复合材料结构的损伤监测与程度评估已成为当前结构健康监测研究的热点之一。

复合材料结构形式往往较为复杂，损伤也呈现出多样化特征。现有结构健康监测研究中，基于结构模态参数的损伤评估方法，如固有频率法、频响函数法等，应用于早期的损伤监测时，由于损伤对结构的整体参数影响较小，不易产生明显的变化，从而使得此类方法对早期微损伤的发现，以及损伤演化的规律难以掌握[2-4]。基于机电阻抗技术的损伤识别是近年来的另一项研究热点，该方法对局部损伤敏感，且不受结构复杂集合形状的限制，但依赖模型，同时压电传感器也受温度影响较大[5-6]。基于Lamb波的结构损伤监测技术利用结构损伤对Lamb 波信号传播的作用机理，结合先进的信号处理方法进行损伤的判断，由于其对微小损伤敏感、传播距离远，被认为是最具应用前景的一种监测方法。在典型结构损伤定位、基于压电阵列的损伤评估方面，形成了许多有实用价值的研究成果。然而，复合材料结构损伤的形成与发展过程较为复杂，影响因素众多，结构中的Lamb波传播也存在多模、频散、各向异性等复杂性，造成损伤的评估与跟踪监测研究难度大。现有的基于时域波形变化等特征的Lamb 波损伤监测方法，由于可用信息较局限，因此很难反映复合材料结构状态和损伤的变化过程。

针对这一难点问题，通过对复合材料结构中传播的Lamb波响应信号多尺度分析，分析、发现和提取反映结构损伤发生、发展变化的多特征参数，并借助于神经网络的非线性映射能力，研究复合材料结构损伤的跟踪监测[7-9]，借此探索解决复合材料结构的典型损伤评估问题，为保障结构安全提供可行的思路。

1 基础分析

1.1 Lamb波的基本原理

Lamb 波是一种在具有两个平行表面结构中的横波与纵波相互耦合而形成的弹性波。由于Lamb波传播过程十分复杂，因此易受到频率、板厚等参数的影响[10-11]。依据经典弹性力学，可以获得板结构中传播的Lamb波频散方程，为简化描述，各向同性材料板结构的频散方程可表述为

其中：D是板的厚度；α2=(ω2/c21)- k2；β2=(ω2/c22)-k2；ω是角频率；上标正号对应于对称模式S；上标负号对应于反对称模式A；c1为横波波速；c2为纵波波速；波数k=ω/c3，c3是Lamb 波的相速度。

求解上述频散方程，根据板表面的质点相位关系，可以将Lamb波分对称波与反对称波，而每种波又具有多种模式。典型的各项同性板结构中传播的Lamb波频散曲线如图1 所示。由图中可知，在低频厚积的情况下，Lamb 波传播主要以A0、S0 两种模式为主，随着频厚积的增加，会产生更多的模式，并且对信号的解释与研究将趋于复杂化。通常，S0 和A0 两种模式都可以用于损伤的识别。由于传播过程中的速度不同、板结构上下点位移动的运动方向不同，两种模式会对损伤有不同的响应。一般来说，在相对低的频厚积范围内，S0 模式会有更快的传播速度，而A0 模式则相反[12]。复合材料是典型的各向异性材料，其各向异性特性受铺层、纤维材料属性、树脂材料参数等影响，因此建模方法、频散曲线求取等相比于各向同性材料更为复杂[13-15]。

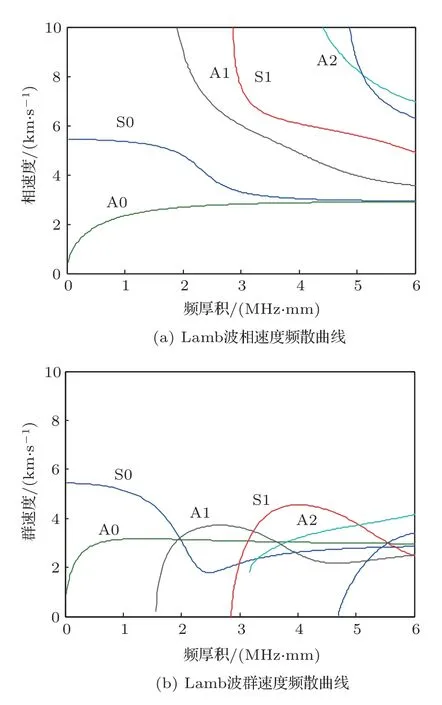
图1 Lamb 波传播的频散曲线Fig.1 Dispersion curve of Lamb wave propagation

1.2 小波多尺度分析理论

小波分析是利用一小波基函数通过伸缩和平移去表示、逼近某一信号或函数，而小波包可以克服小波在高频信号上的分解能力不足。小波包的分解过程实质上是信号进行带通滤波的过程，由式(2)～(3)小波包快速分解的算法可知，信号的分解过程实际上是通过小波包系数p与带通滤波器H、G进行卷积后再隔点进行采样分析的结果，每进行一层信号的分解，数据都将成倍减半，对信号的高低频部分进行分解，被分解的信号可以划分到任意的频段上。因此，采用小波包分析提取到的各个频段的信号特征信息，可以将其用于损伤程度评估上。

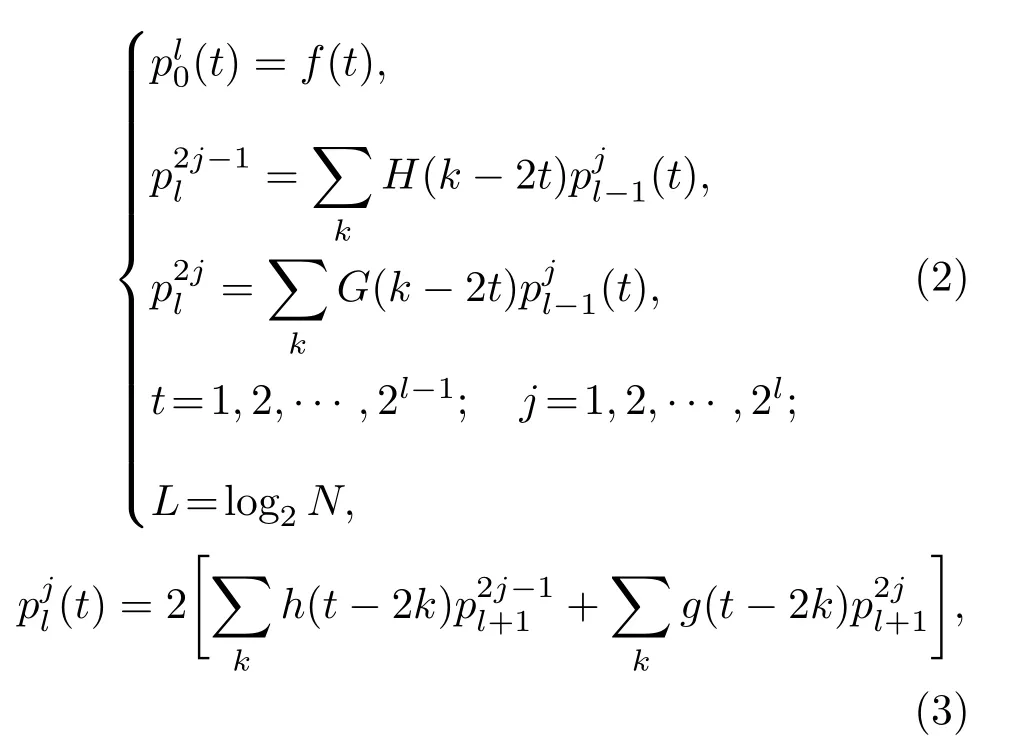
其中，pjl为第l层的第j个小波包系数，l为分解层数，N为信号长度；G、H为小波包分解滤波器；g、h为小波包重构滤波器。

Lamb 波是一种非平稳信号，而时频域分析法中小波包方法能够较好地逼近Lamb 波信号，克服时域到频域中转换的不足。同时该方法对发现由于损伤引起的Lamb 波模式变换、频率变化等信息比较有效，因此可以用来提高损伤评估的准确率。

2 损伤监测机理分析与特征提取

2.1 Lamb波响应信号的分析

复合材料的损伤形式多样，典型的损伤包括塑性断裂、分层、裂纹、通孔和孔隙等。不同的损伤，其损伤特征也有所不同。结构损伤的发生，对Lamb波响应信号的作用机理较为复杂，单纯地从时间域和频域进行分析，难度较大，且特征参数单一。通孔损伤是最为典型的一种外部作用下引起的复合材料结构损伤形式，为了方便研究，本文选择此类损伤作为典型损伤，开展机理分析和方法研究。在玻璃纤维环氧树脂复合材料板上，以一个压电片作为激励器，激发Lamb 信号，另一个作为传感器，接收到的结构损伤前后响应信号如图2所示。

传统损伤监测方法一般是依据时域信号中的变化来提取有关损伤的信息。从图2 可以较为清楚的看到，除了在时域波形上，存在一定的差异性之外，在频域中，损伤会引起频谱的改变，例如损伤发生引起的信号低频和中心频率削弱、高频部分的扩展等。因此，损伤引起的信号变化是体现在多个方面的，但同时也是十分复杂的，单纯地从时域进行信号特征分析和提取显然是不充分的，对于探究损伤引起的响应信号变化以及对损伤程度和发展过程的估计，支撑不足。因而，利用时频域进行综合的特征分析与提取，有利于进一步理清损伤对结构响应信号的作用情况，进而通过多个特征，表征损伤的发生和发展情况。

下面进一步对图2所示的损伤前后结构响应信号进行分析，其具体的无损情况下Lamb 波结构响应信号的时域与频域波形图如图3(a)和图3(b)所示。进行小波包变换后，得到了如图3(c)所示的时间频率图。小波包3 层分解之后，将信号频率分成了8 个区间，每个区间占62.5 kHz，在图3(c)中可以看到，其中最低的两段颜色最重，说明了信号频率主要集中在这两个频段之间，即0～62.5 kHz 和62.5～125 kHz 之间，其余频段基本没有频率分布。采用相同的思路，对其他不同程度损伤下结构响应信号的时间频率图进行分析，分析信号主要的频率分布，比较不同程度损伤的小波包分解的第3 层能量集中程度，可以得到如图4所示的能量分布图。

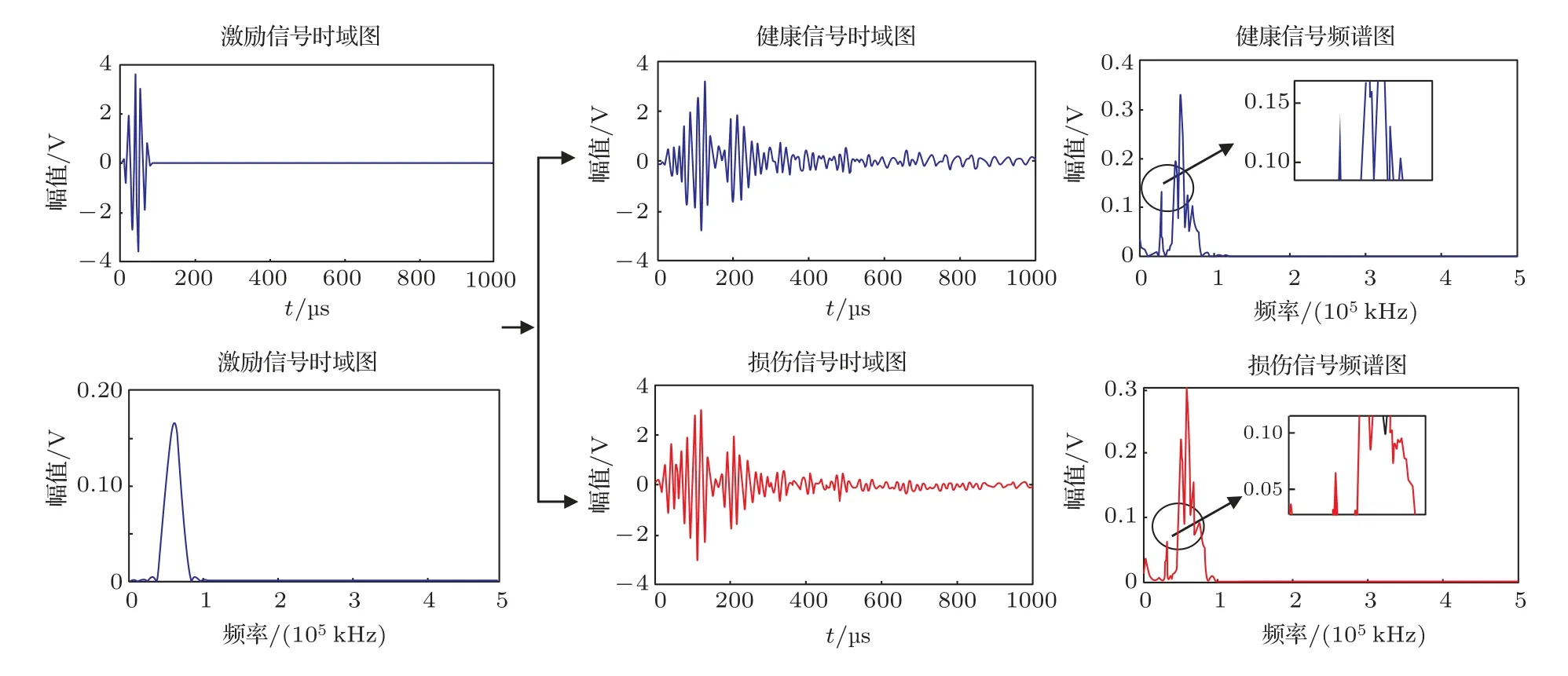
图2 Lamb 波结构响应信号时、频域分析Fig.2 Time domain and frequency domain analysis of Lamb wave structure response signal

从图3 中可以看出，能量主要集中在第3 层的第1、2两个节点。根据图3、图4所示的分析结果，将信号转化到时频域中，可以利用损伤引起的信号能量变化以及小波包系数变化，计算提取出时域上的波形特征、波峰特征和频域上的能量百分比、能量分布等多个特征参数，从多维度分析损伤的发生、发展情况等。

图3 无损状态下Lamb 波结构响应信号的时域、频域和时频域分析Fig.3 Time domain,frequency domain and time-frequency domain analysis of Lamb wave structure response signals in lossless state

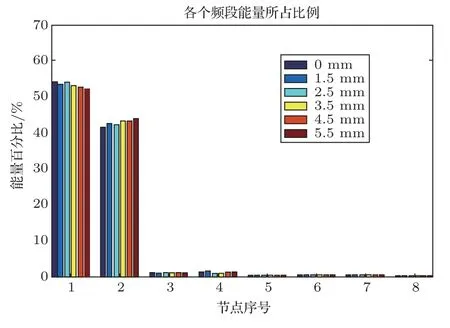
图4 不同损伤程度(通孔)能量分布对比图Fig.4 Comparison of energy distribution of different damage degree(through hole)

2.2 特征参数提取

针对不同程度损伤，进行小波变换多尺度分析时，需确定小波基函数，而小波基函数的确立主要从它的紧支性、正则性、消失距、对称性、支集长度这几个方面考虑。Lamb波的信号是一个非平稳信号，因此它具有瞬态性以及复杂多样的特征。为了更好地获得其局部特性，应尽量考虑其在时域的紧支特性，也需确保小波基在频域上拥有一定的能量分析能力，因此应选择具有频带快且速度衰减慢的小波基函数。正则性较好的小波基可以较好地描述信号的能量特征。拥有较好对称性的小波基，则可以减少信号存在的边缘失真，合适的消失距则对信号的高频噪声具有抑制作用。结合以上的分析，选取了DaubechiesN系列的db4小波基函数。

对采集到的信号进行3 层全分解，最后一层就是23= 8 个频率段。这8 个频段则包含了信号的高低频信息。结合数理统计分别定义了4 个特征参数：波形特征Wf、波峰特征Wp、能量分布Ed、能量百分比E，以第l层的第j个节点(即第j个频段)为例，Wf反映j节点重构信号的时域波形特征，Wp反映波形重构信号的峰值特征，Ed反映第j节点信号的频域能量分布情况，E反映j节点信号频域能量占一层信号总能量的百分比。各参数式定义如式(4)～(7)所示。

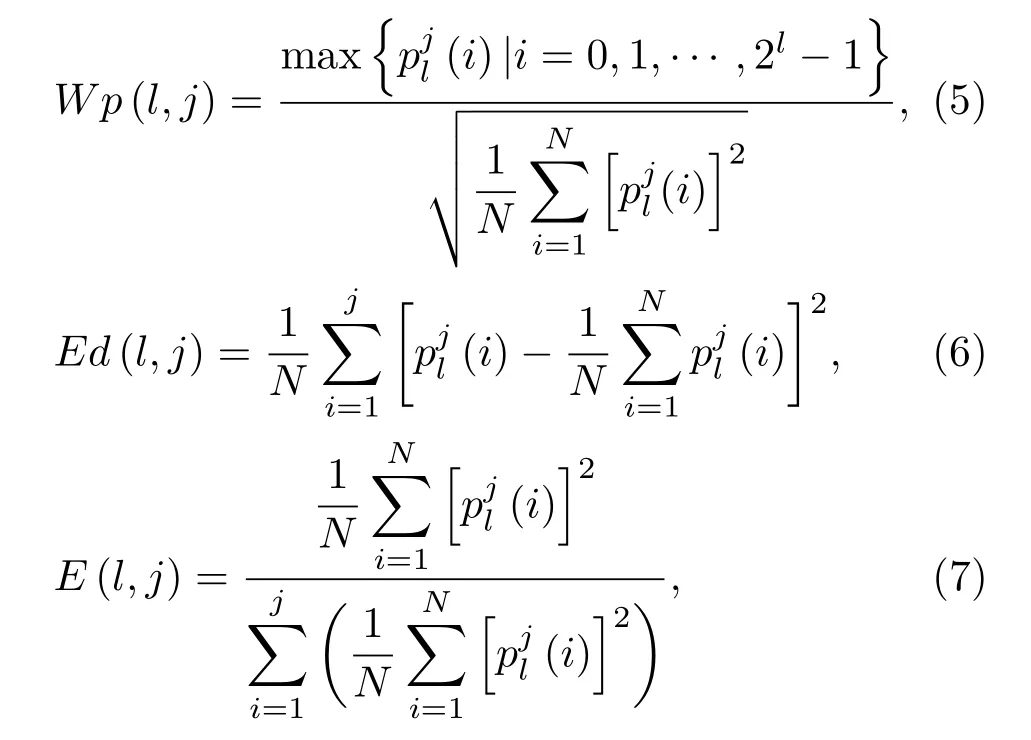
其中，pjl示分解后l层上第j个节点的小波包系数，该系数是离散的，N为系数的长度。

2.3 特征参数可分性比较

在损伤程度评估时，特征参数的选择通常能够提高程度评估的准确率。选取那些在区别度上较大的特征，而弃去那些对分类影响较小的特征，从而得到反映损伤分析本质的特征。本文选择常用的欧式距离(如式(8)所示)，作为特征的判断方法，欧式距离越小，表示特征之间就越相似，并在基础上定义损伤特征的类内距离(式(9))、类与类之间的类间距离(式(10))作为判断依据。

在同种程度损伤中组成的特征向量的集合{x}，类内距离可表示该集合中特征向量的分散程度，值越小，表示越相近；而类间距离表示不同程度损伤的特性向量之间的差异。当任一不同程度的损伤特征向量的类内距离大于类间距离，则可认为该种程度的特征向量具有较好的可分性。并在此基础上，提出损伤程度的可分性判据JX,Y(式(11))，JX,Y小，则表明X、Y两种程度的损伤可分性越好。

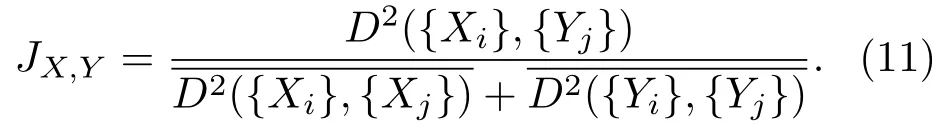
3 损伤程度评估

3.1 基本思路

复合材料损伤机理十分复杂，利用固有频率、频响函数等系统固有参数作为指标，很难找出明确的函数关系，而且对损伤的出现的时期、识别效果等也会在众多因素影响下产生较差的效果。神经网络可以通过对系统提取的损伤样本进行自动的学习，能够以较高的精度去逼近由于损伤造成的非线性映射，因此，在损伤程度评估中利用这一特性，构建损伤评估模型。BP 网络是一类多层的前馈神经网络，由于它具有结构简单、可用于设置的参数多、训练算法较好及可操作性简便等特点，获得了非常广泛的应用。单隐含层神经网络模型在神经网络中广泛的应用，它包括了输入层、隐含层以及输出层。本文将神经网络与智能算法相结合，对复合材料的不同程度损伤进行评估。

遗传算法(Genetic algorithm,GA)是一种借鉴生物进化过程和自然选择机制而发展起来的高度并行、自适应搜索的全局优化算法。使用遗传算法对BP 神经网络进行优化，可以实现网络参数最优。这一优化包括3 部分，分别为确定BP 神经网络结构、遗传算法优化网络的权值与阈值、BP 神经网络进行损伤程度预测。

3.2 损伤评估模型的建立

对采集到的信号进行小波多尺度分析后，分别提取多尺度特征参数：波形特征Wf、波峰特征Wp、能量分布Ed、能量百分比E，建立损伤信息标准库。在损伤识别中，采用神经网络进行评估。将损伤样本分为训练样本与测试样本，然后训练以及测试神经网络，最后利用未知损伤对系统进行验证。模型如图5所示。

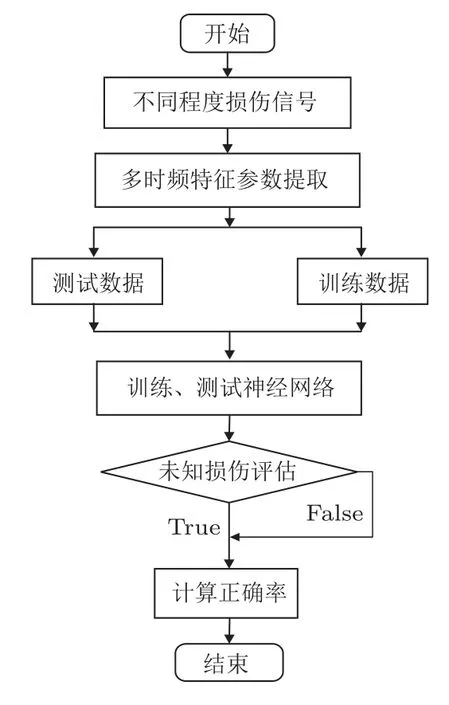
图5 损伤程度评估模型Fig.5 Damage assessment model

4 实验验证与结果分析

4.1 损伤评估系统设计

本文将损伤评估的系统分为3 个模块，分别为损伤信号监测、损伤信号分析与处理、损伤程度评估，如图6 所示。损伤信号监测模块主要由数据采集设备、功率放大器、电荷放大器、待测结构组成。该模块利用结构在线监测技术，针对待测结构的物理情况，设计传感阵列，通过上位机激发Lamb波信号。由于上位机激发信号的幅值有限，而Lamb波在结构中传播信号会衰减，因此需要利用功率放大器对激励信号进行放大。压电传感器接收的信号幅值大约在25 mV左右，通过电荷放大器将压电传感器接收到的信号进行放大、滤波。最后利用上位机将接收到的信号进行存储[16-17]。

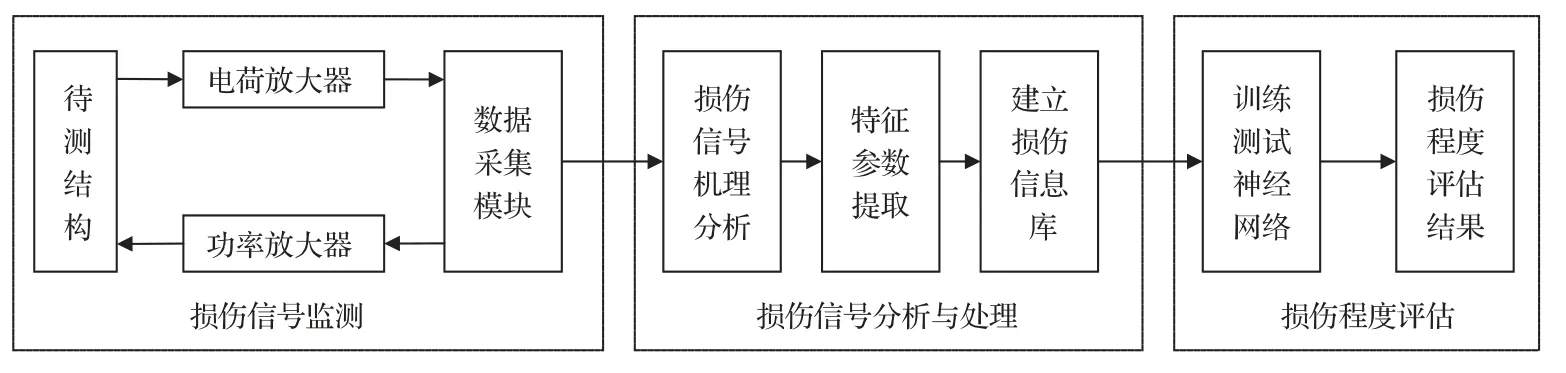
图6 损伤程度评估系统框架Fig.6 Framework of damage assessment system

在损伤信号分析与处理模块中，对采集的信号利用时频域分析方法进行损伤信号的机理分析。根据时频域上特征参数的变化，提取时域上的波形特征Wf、波峰特征Wp与频域上的能量分布Ed、能量百分比E作为损伤的特征向量，建立损伤信息标准库。

损伤程度评估模块是通过神经网络来实现，评估过程包括从损伤信息标准库中选取损伤样本集，将其分为训练集与测试集，然后训练与测试神经网络，最后用未知损伤去验证网络的评估正确率。

4.2 实验方案设计

实验采用的材料为玻璃纤维环氧树脂复合材料板，其大小为1000 mm×500 mm×3 mm，它的密度为1960 kg/m3，杨氏模量是20 GPa，泊松系数是0.17[18-19]。根据Lamb 波传播频散特性，为了获得模态简单易于识别而便于信号分析与特征提取的响应信号，兼顾时间分辨率和频率分辨率，选用窄带激励信号，中心频率限制在20～200 kHz 区间，激励出A0或者S0模态为主的激励信号(如图1所示)，经过分析和实验测试，选定中心频率为60 kHz。实验中采用的系统设备如图7所示。

图7 实验设备图Fig.7 Experimental equipment diagram

实验中，采集不同程度损伤的数据，由于不同损伤程度的样本较多、数据较大，所以采用了单一线性阵列作为实验传感阵列。为了尽可能多地获得和分析实验数据样本，传感阵列布置了4 行6 列共24个传感器。

如图8 所示，激励和接收相距12 cm，每一对激励接收传感器为一单一线性阵列。在复合材料板上模拟不同程度的损伤，通过模拟典型损伤通孔，分别在纵向路径上制造出大小为0 mm、1.5 mm、2.5 mm、3.5 mm、4.5 mm、5.5 mm。在横向路径上模拟3种不同程度的裂纹损伤，分别为无损、损伤程度20%和损伤程度50%。

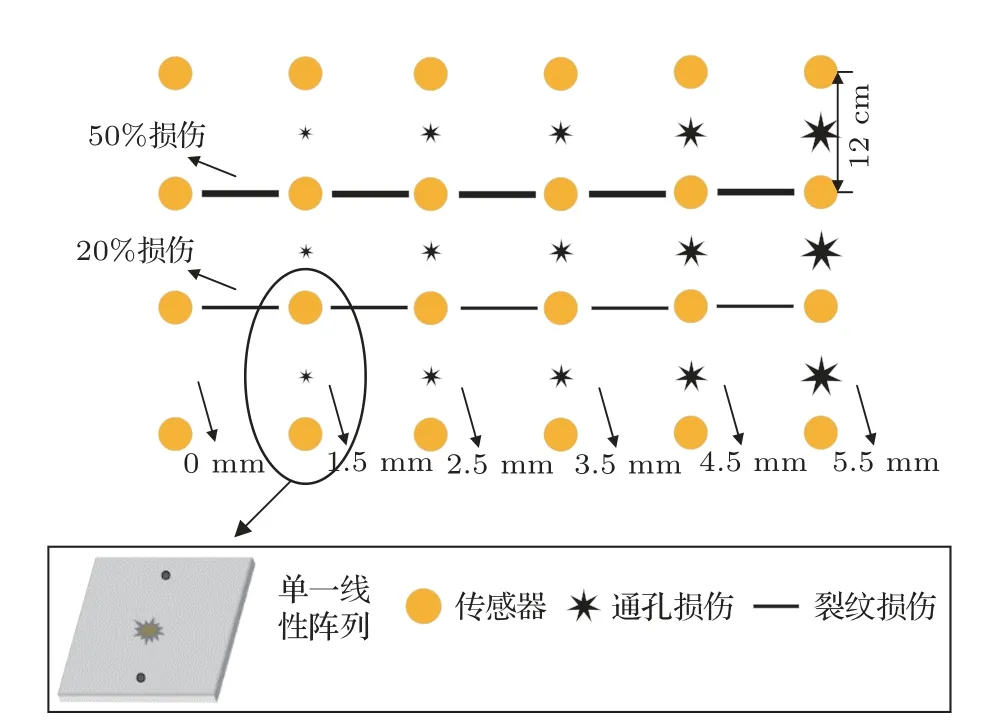
图8 多个线性阵列布置方案Fig.8 Multiple linear array layout

在纵向路径上，模拟通孔大小，分别采集6 种不同程度的损伤，得到了486 组信号。在横向路径上，则模拟裂纹损伤，分为3 种程度，共采集到252组信号。

4.3 实验结果分析

实验提取到的特征参数本身具有一定的物理意义，同时与其他的特征参数也存在不同的量纲，因此，需要对提取到的特征参数进行尺度上的归一化处理。归一化后的不同程度的损伤，对典型损伤通孔(0 mm，1.5 mm，2.5 mm，3.5 mm，4.5 mm，5.5 mm)的时域特征向量、频域特征向量、时频域特征向量3 种特征向量分别进行了可分性比较。根据上面计算的波形特征Wf、波峰特征Wp、能量分布Ed、能量百分比E，分别定义3种特征向量的如下：

(1)时域的特征向量：[Wf0,Wf1,··· ,Wf7,Wp0,Wp1,··· ,Wp7];

(2)频域的特征向量：[Ed0,Ed1,··· ,Ed7,E0,E1,··· ,E7];

(3)时频域的特征向量：[Wf0,Wf1,··· ,Wf7,Wp0,Wp1,··· ,Wp7,Ed0,Ed1,··· ,Ed7,E0,E1,··· ,E7]。

同种程度损伤特征向量归一化之后的类内距离的统计如图9 所示。可以看出，同种程度的损伤特征向量时频域中的差异性较大，计算它们的均值和均方差分别为时域(0.7466/0.0229)、频域(0.7579/0.0046)、时频域(0.7759/0.0462)，可以得到时频域的均值和均方差均要大于时域和频域的均值和均方差，说明时频域的可分性较好。图10 显示了不同种程度损伤特征向量归一化后的类间距离统计，图11 为不同程度损伤特征向量的可分性比较。从图9～图11可以看出时频域中的特征向量的类间距离均小于同种程度特征向量的类内距离，同时计算它们的均方差分别为(时域0.018、频域0.013、时频域0.004)，可以发现它们之间的均方差较小，说明提取的特征向量分布比较均匀，特征之间的差异性较大，不同种损伤的可分性较好。但对于两种不同程度的损伤特征向量进行比较，可以发现它们的可分性判据上下波动不一，而损伤信号的波形复杂多样，在时域上存在较多影响特征的因素，所以仅靠时域上的波形特征向量去评估损伤程度，会降低评估的可靠性与准确性；在频域向量上，可分性波动较大，不稳定，因此可分性较差。

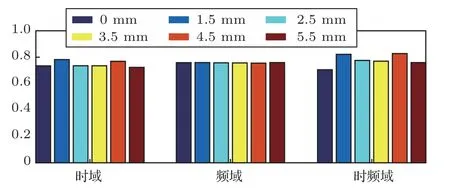
图9 同种程度损伤特征向量的类内距离比较Fig.9 Comparison of within class distance of feature vectors with the same degree of damage

图10 不同程度损伤特征向量的类间距离比较Fig.10 Comparison of distance between different damage feature vectors

图11 不同程度损伤特征向量的可分性比较Fig.11 Comparision of separability of different damage feature vectors

为了能够保证损伤程度的可靠性与准确性，选择时频域上的损伤特征向量作为损伤程度评估的特征参数。

从损伤样本信息库中选取6 种不同程度通孔损伤样本各80 组，然后采用遗传BP 神经网络进行训练，将样本分为测试样本各16 组，训练样本各64组。经过训练后，BP神经网络在隐含层神经元个数到达30 时，训练误差和测试误差都到达最小；对于GA-BP 神经网络，使用遗传算法后，无论在训练误差还是测试误差，都比BP神经网络要小很多。在隐含层神经元数目到达30时，其训练误差和测试误差都达到了最小。因此，在考虑训练误差和测试误差下，选择神经网络的结构为32-30-6。

在进行神经网络训练时，由于每次选取的测试样本和训练样本以及网络的初始权值都有一定的随机性，造成网络最后的结果具有差异性，这样就要求网络需要较强的泛化能力。因此，为了比较BP神经网络与GA-BP 神经网络的准确性与稳定性，按照前文所述的网络结构，分别进行10次的训练和测试，其公式如式(12)所示：

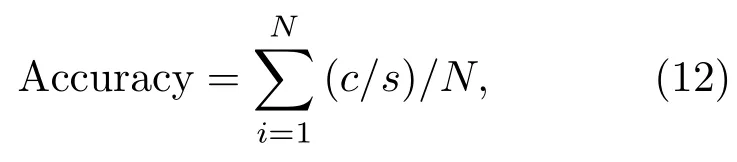
其中，c为正确数，s为样本数，N为测试次数。分别使用均值和均方差对网络的各个参数进行分析。在正确率上，均值可以很好地反映网络的各个不同程度损伤的识别能力；均方差则能够反映在多次训练中，网络的稳定性好坏，均方差越小则说明网络的泛化能力越强。

从表1以及图12中可以得出以下结论：

图12 BP 神经网络与GA-BP 神经网络的通孔损伤正确率比较Fig.12 Comparison of correct rate of through hole damage between BP neural network and GA-BP neural network

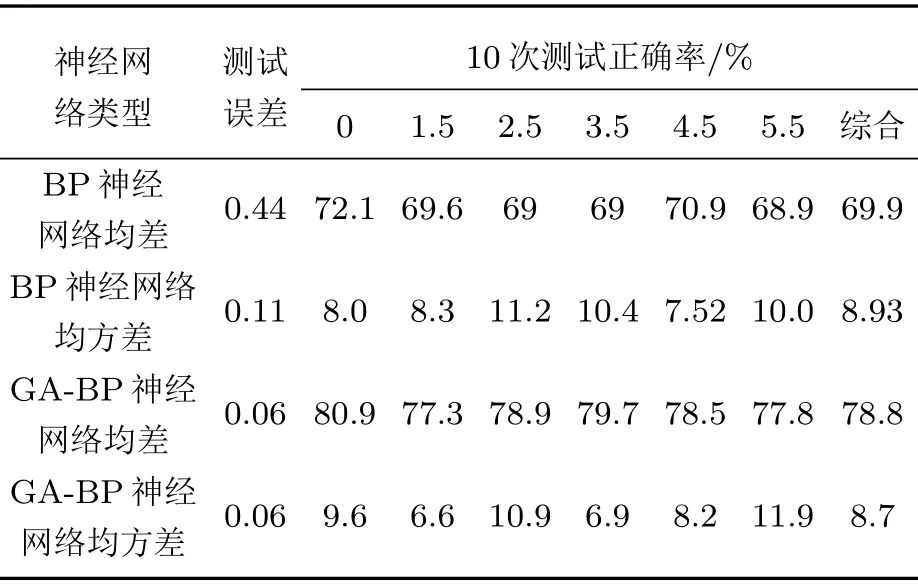
表1 不同神经网络测试正确率Table 1 Test accuracy of different neural networks

(1)从均值可以看出，GA-BP 神经网络的评估正确率要高于BP 神经网络。GA-BP 神经网络6中不同程度的损伤评估平均正确率分别为80.9%、77.3%、78.9%、78.9%、78.5%、77.8%，BP 神经网络6 中不同程度损伤的评估平均正确率分别为72.1%、69.6%、69%、69%、70.9%、68.9%，两种神经网络的综合均评估正确率分别为78.85%、68.9%。表明使用遗传算法优化后的网络权值和阈值，网络的评估正确率则明显高于单一BP 神经网络。从训练过程中可以发现，网络只需要经过较少的训练就可以达到很好的识别结果。

(2)尽管GA-BP 神经网络的测试误差要小于BP 神经网络，但是在均方差上而言，BP 神经网络网络泛化能力稍微高于GA-BP 神经网络。总体而言，使用GA-BP 神经网络去做损伤程度评估，将有效提高网络的评估正确率，从而减小工程应用中的误差。

为了测试系统的泛化能力，再选取裂纹损伤程度进行评估。从样本信息库中选取每种损伤程度样本集各80组，将其中的64组分为训练集，16组分为测试集。由于评估的裂纹损伤程度为3 种，因此，神经网络的输出节点设置为3。网络经过训练后得到隐含层神经元的个数为28，最后得到的整个网络的结构为32-28-3。

表2 为3种不同程度裂纹损伤评估正确率。BP神经网络的评估正确率分别为81.25%、75%、75%，GA-BP 神经网络的损伤程度评估正确率分别为87.5%、87.5%、93.5%。从每种程度的损伤评估正确率和整体正确率上看，GA-BP 神经网络均要高于BP 神经网络。裂纹损伤评估正确率整体均大于通孔损伤的正确率，主要原因是裂纹的损伤程度种类比通孔要少3种，这大大降低了网络的复杂性。

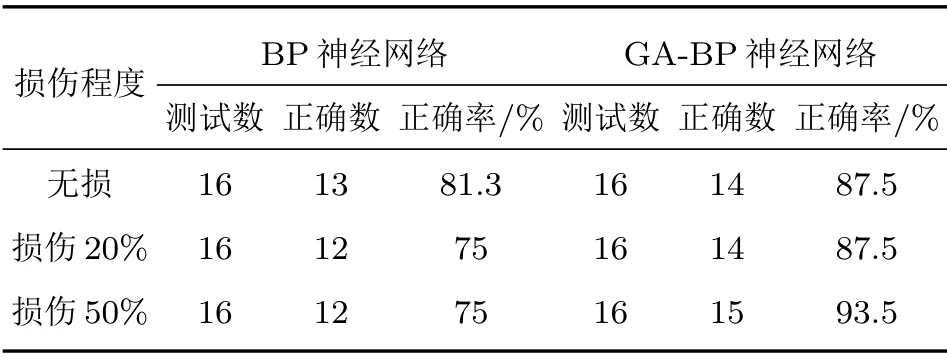
表2 不同程度裂纹损伤识正确率Table 2 Accuracy of crack damage identification indifferent degrees

5 结论

本文对复合材料的不同程度损伤进行评估，并设计了相应的配套系统。通过结构健康监测技术进行损伤的在线监测，利用信号分析方法中的小波包分析法对损伤信号进行时域与频域上的分析，提取了时域特征参数(波形特征Wf、波峰特征Wp)和频域特征参数(能量分布Ed、能量百分比E)，建立损伤特征向量，构建了损伤信息标准库，利用两种神经网络对不同程度的损伤进行评估。

针对系统的准确性与可靠性，设计实验进行了验证。分别采集了通孔、裂纹两种损伤进行验证。裂纹损伤分为3 种不同程度，从实验的结果可以得出：BP 神经网络评估正确率在75%以上，GA-BP神经网络的损伤程度评估正确率达到87.5%以上，具有较高的正确率。通孔损伤则分为6 种不同程度，GA-BP 神经网络与BP 神经网络的综合均评估正确率分别为78.85%、68.9%，表明在一定程度上也能够完成损伤程度的预测。两种损伤的准确率出现的差距主要是由损伤程度种类的不同而产生了较大的影响。从整体上看，该损伤程度评估系统能够对未知损伤进行预测，降低安全隐患，为维修提供指导意见。