基于双稳态非线性能量阱的轴承-轴悬臂系统振动抑制研究

温晓蕾，李妙玲，陈智勇,，徐颖强，姚永玉

(1.河南水利与环境职业学院 土木工程系，郑州 450008；2.洛阳理工学院 智能制造学院，河南 洛阳 471023；3.西北工业大学 机电学院，西安 710072)

随着科学技术的发展，对轴承的振动质量提出了更高要求。如何降低工作中轴承的振动，是轴承应用领域的重要技术难题。利用吸振技术对配套主机进行振动控制是有效的振动抑制手段，但目前传统吸振器吸振频带狭窄，对宽转速轴承减振效果不明显。

国内外学者针对基于能量阱的减振控制进行了大量的研究：20世纪中叶，文献[1]提出吸振器添加非线性刚度元件——非线性能量阱(Nonlinear Energy Sink，NES)进行振动控制，非线性能量阱可有效拓宽减振频带，且附加质量小，稳定性好；文献[2]对NES靶能量传递进行了深入研究，证明系统能量可单向传递至NES中，且其具备附加质量小，减振频带宽，可靠性高等优点；文献[3]证明能量阱可以快速吸收耗散梁的大部分振动能量，并基于能量耗散率优化了能量阱在梁上的安装位置；文献[4]将能量阱附加在机械臂上，利用数值法分析了能量阱的工作性能；文献[5]研究表明，能量阱可以有效抑制星载飞轮在瞬态激励和稳态激励下的振动；文献[6]利用振子内部旋转设计了一种能量阱，与纯立方刚度能量阱的对比表明该结构具备更好的减振性能及稳定性；文献[7]研究了冲击载荷下能量阱的减振性能，结果表明能量阱能使船舰快速减振，但能量阱对冲击强度较为敏感，只有达到触发阈值时才可高效减振；文献[8]将能量阱安装在夹层梁内，研究能量阱对梁的振动抑制，结果表明减小能量阱阻尼可提高其工作性能；文献[9]研究了受控系统在附加能量阱后产生高分支响应的条件，并通过串联能量阱在一定范围内消除高分支响应，提高了能量阱在不同激励强度下的减振稳定性；文献[10]基于分段线性构造了非光滑非线性恢复力，建立了轴承系统耦合NES的力学模型，利用遗传算法对NES的结构参数进行了优化，分析了多自由度系统参数的优化问题，试验结果表明，优化后的NES可在更宽的频带内对轴进行振动抑制；文献[11]以能量阱耗散为工作性能指标，分析了能量阱在冲击激励下的减振性能，并研究了能量阱结构参数对触发阈值的影响，结果表明提高非线性刚度可以降低能量阱触发阈值，但非线性刚度过大，会造成强激励下能量阱性能下降；文献[12]研究了在谐波激励下受控系统安装能量阱及压电俘能器时振动控制与能量收获的集成问题，并分析了共振附近的准周期运动对振幅、能量收集带宽的影响；文献[13]利用数值仿真分析了双稳态能量阱各个结构参数对其减振性能的影响，通过对能量阱结构参数的逐次优化，得到了质量比以及调谐频率比的最佳区间，同时兼顾了能量阱减振性能及能量俘获，且只有当外界激励强度达到一定程度时，能量阱才能高效工作。

综上分析，如何降低NES触发阈值，提高NES在低扰动工况下的工作性能具有重要研究意义。双稳态非线性能量阱(Bistable Nonlinear Energy Sink，BNES)的非线性刚度由立方刚度及负刚度构成，可降低能量阱的触发阈值，提高其在低扰动下的工作性能。本文利用线性刚度元件，通过非线性几何关系构建BNES，并耦合于悬臂梁系统进行减振分析；通过数值计算，利用势能函数分析NES触发阈值与非线性刚度比的关系，研究BNES的瞬态、稳态工作性能。

1 轴承系统耦合BNES模型构建

BNES由质量单元、阻尼单元、非线性刚度及负刚度组成。文中利用线性元件，通过几何非线性关系构造非线性恢复力以实现非线性刚度，如图1所示。

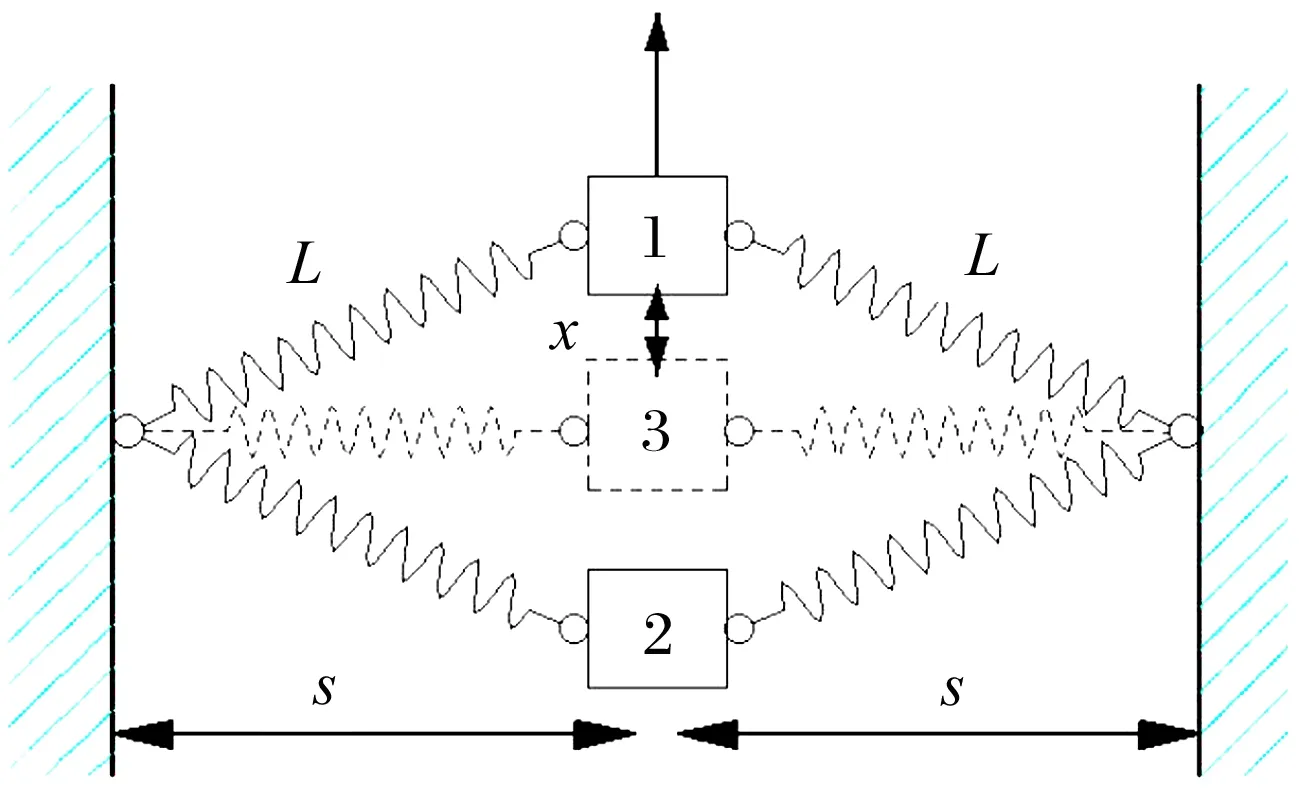
图1 非线性刚度实现

振子在位置3利用2个刚度系数相同的线性弹簧连接，此时为预紧状态；位置1，2为两弹簧自由状态。当振子离开位置3时，可得恢复力F与位移x的关系为

(1)

式中：F为位移x方向的恢复力；k为弹簧的刚度系数；x为偏离位置3的位移；L为弹簧原长；s为振子位于位置3时，弹簧处于压缩状态下的长度。利用麦克劳林公式把(1)式展开为

(2)

F≈-K1x+K3x3，

(3)

当振子的位移满足|x|≤0.4s时，(3)式的误差不高于5%[14]。

将上述BNES安装于轴承系统(即主系统)中，如图2a所示，并将系统简化为如图2b所示的二自由度模型。

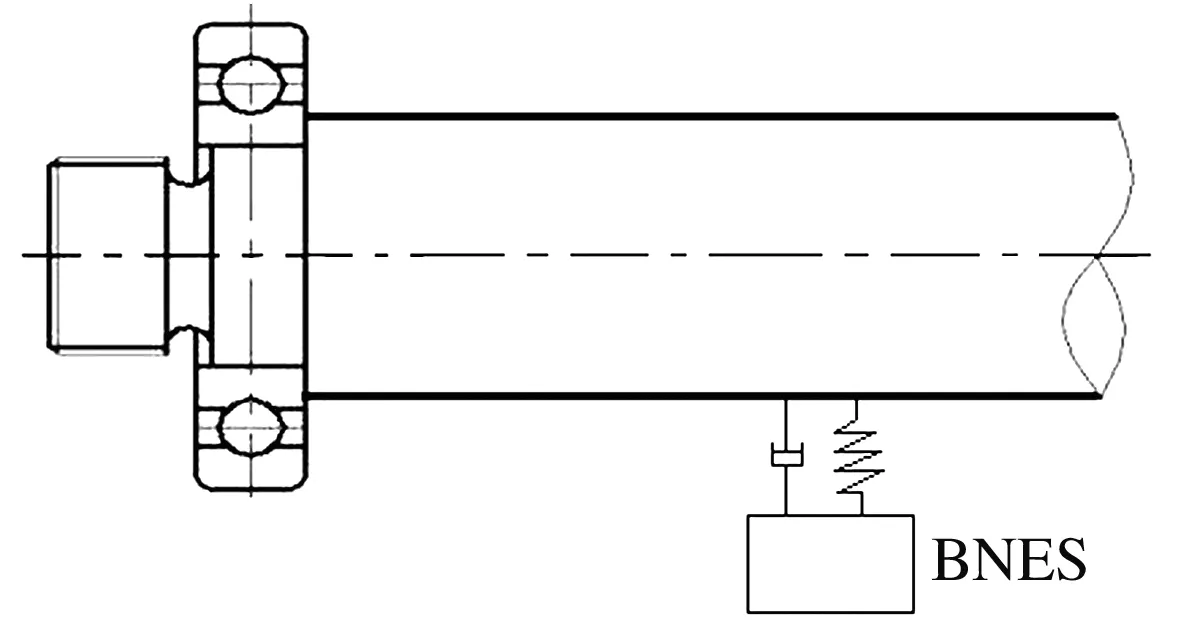
(a)轴承系统安装能量阱示意图

外界激励下系统的动力学方程为

，(4)

式中：mn，m分别为能量阱和轴的等效质量；Cn，C分别为能量阱和轴的等效阻尼；K1，K3分别为能量阱负刚度和立方刚度；K为轴的等效刚度；X，Y分别为能量阱和轴的位移；F(t)为激励。

谐波激励Fcos(ωt)下，对(4)式进行量纲一化得

，(5)

ζn=Cn/(2mnωn)，ζ=C/(2mωn)，

τ=ωnt，k1=K1/K，k3=L2K3/K，

x=X/L，y=Y/L，f=F/(KL)，μ=mn/m，

式中：ω，ωn分别为外界激励频率、主系统固有频率；t为时间。

2 平衡点稳定性分析

本节利用劳斯-赫尔维茨法则对系统的平衡点进行分析。

首先，取x1=x，x2=y，x3=x′，x4=y′，则(5)式的一阶微分形式表示为

(6)

由(5)式可知

(7)

令

(8)

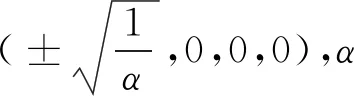
由(5)式可求得平衡点(0,0,0,0)对应的雅可比矩阵为

(9)

对应的特征方程为det(J1-λI)=0，则

a0λ4+a1λ3+a2λ2+a3λ+a4=0，

(10)

a0=1，a1=2ζ+4ζn，

根据劳斯-赫尔维茨可知，(8)式由上述特征系数组成的劳斯-赫尔维茨行列式为

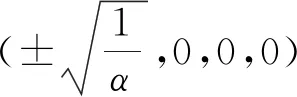
(11)

对应的特征方程为det(J2-λI)=0，则

b0λ4+b1λ3+b2λ2+b3λ+b4=0，

(12)

b0=1，b1=2ζ+4ζn，

Δ1=b1=2ζ+4ζn>0，

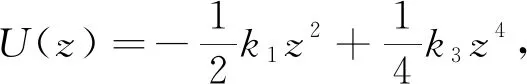
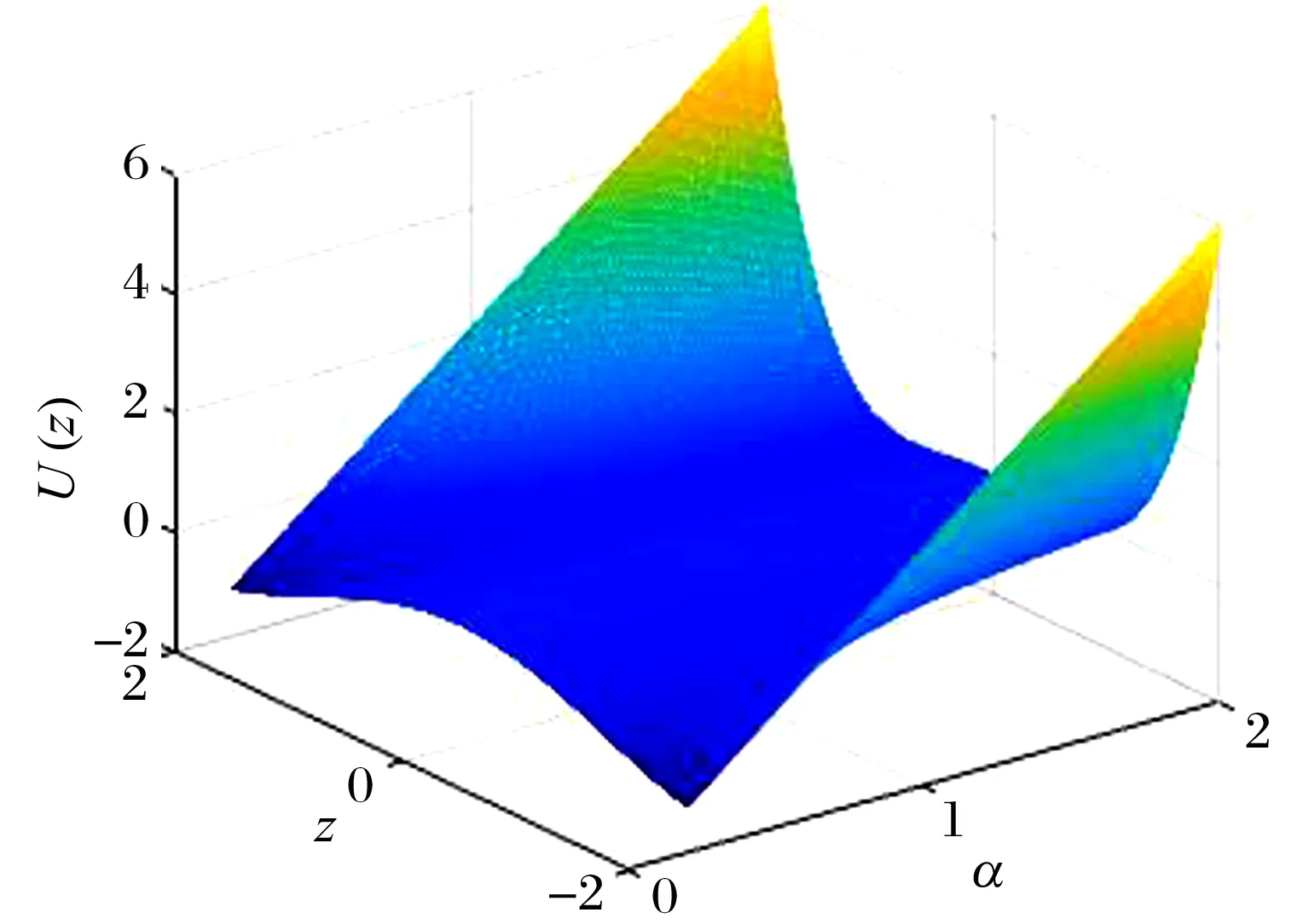
图3 非线性刚度比对势能函数的影响

由图3可知，势能函数存在1个势垒和2个势阱，在BNES跨过势垒做阱间大幅振荡时，BNES高效减振，且势阱深度随非线性刚度比α的变大而降低，故通过调节非线性刚度比可以控制势阱深度，进而改变BNES的触发阈值。

3 BNES减振性能分析

3.1 瞬态减振性能分析

利用集中参数模型，根据(5)式建立的二自由度动力学方程，分析BNES的减振性能。系统中参数设置为：μ=0.05，ζn=0.01，k1=0.1，k3=1，ζ=0.05，ωn=2rad/s，主系统初始条件为x(0)=y(0)=x′(0)=0，y′(0)=0.45，对所有物理量进行量纲一化处理，并利用四阶龙格库塔法进行数值分析。

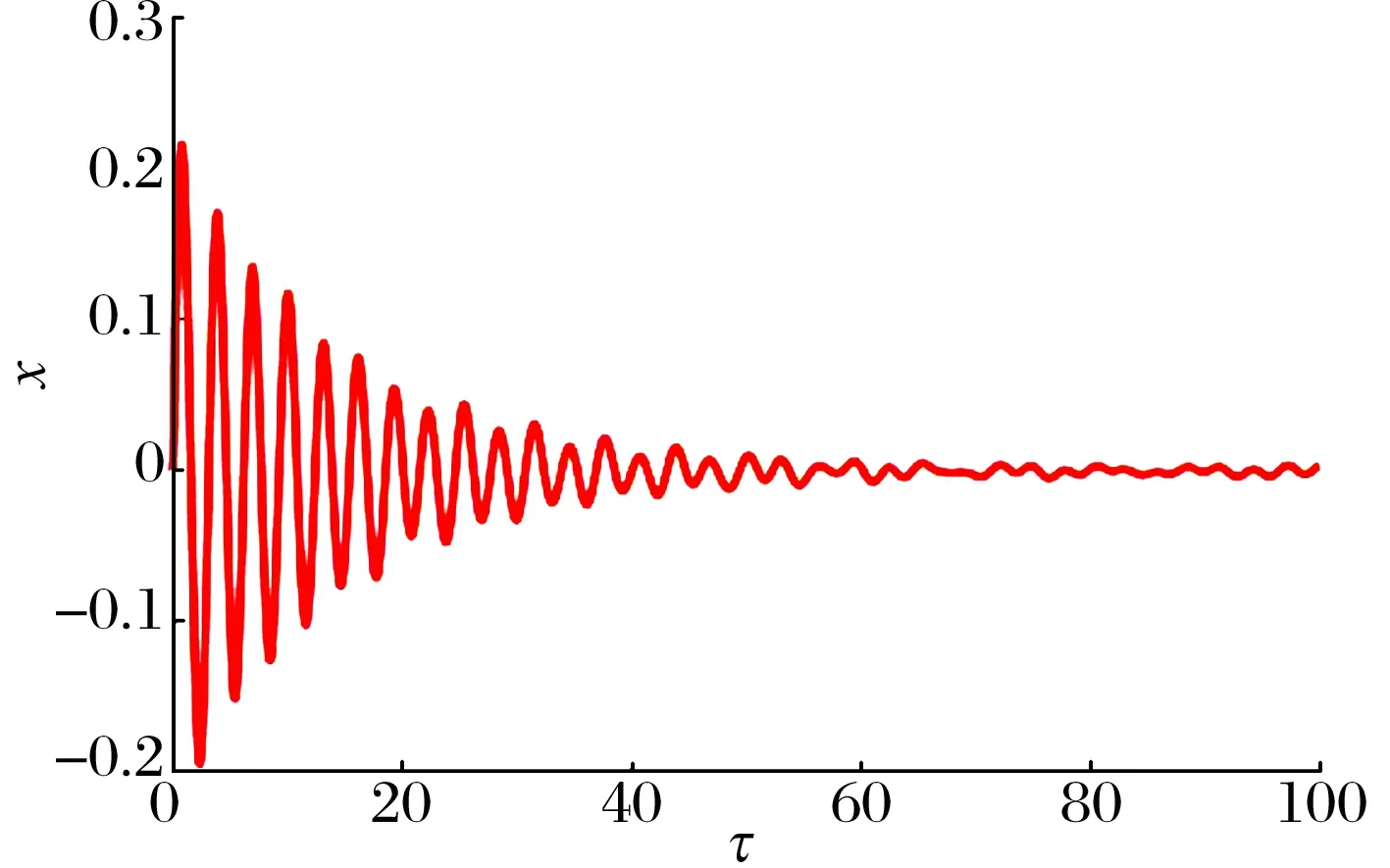
为表明BNES的减振性能，对比分析了有无安装能量阱时主系统的时域响应，结果如图4、图5所示。由图4可知，在初始条件下，主系统随时间做衰减振动，利用本身阻尼耗散初始能量，至τ=100时，主系统仍有较大振幅。由图5可知，在BNES作用下，主系统振动快速衰减，在约τ=50时，振幅趋于0。

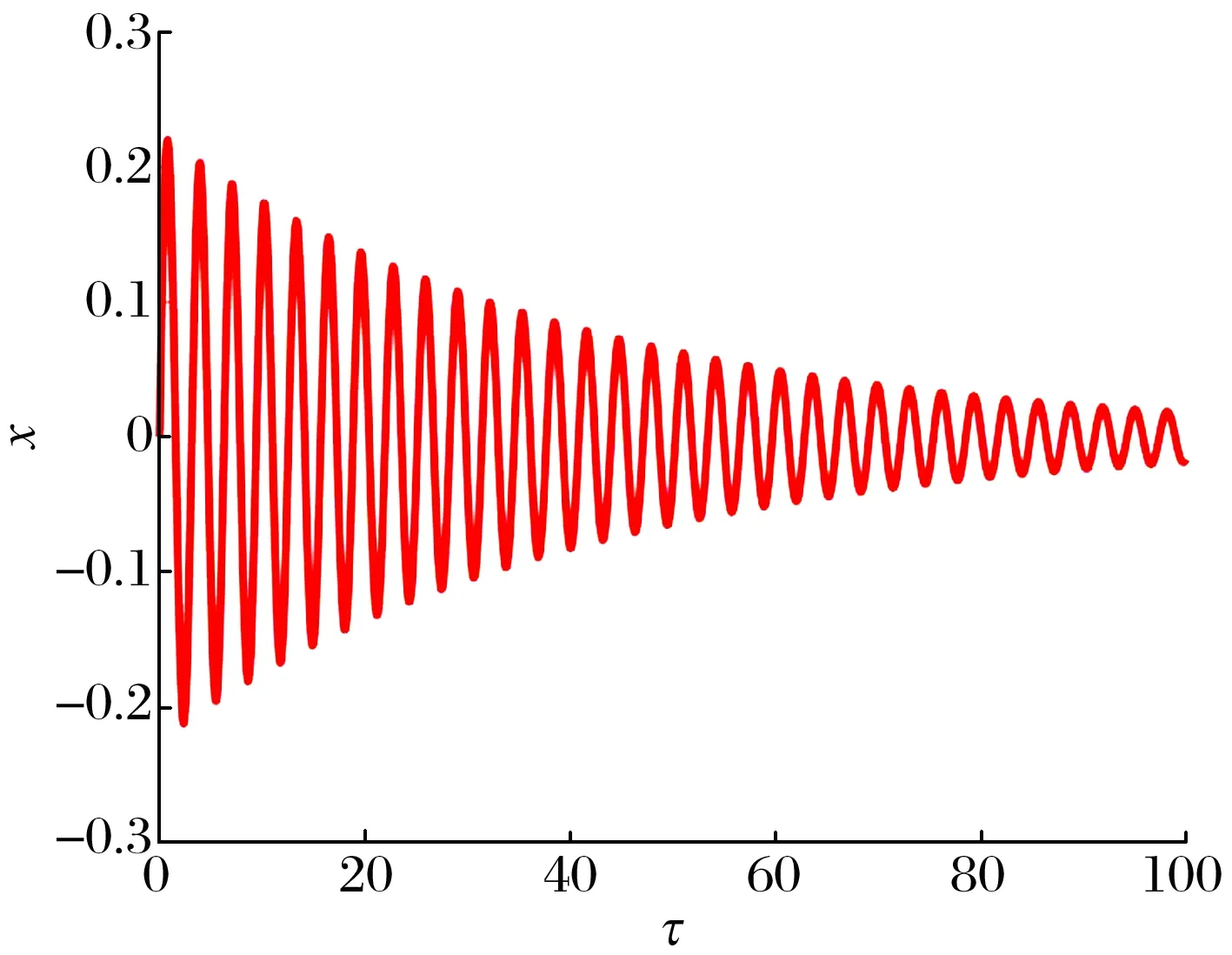
图4 无BNES时主系统的时域图

(a)主系统的时域图

主系统与BNES的小波图如图6所示，τ=0至τ=19间主系统和BNES发生1∶1共振及谐波共振，在τ=36时主系统振幅接近零。

(a)主系统小波图

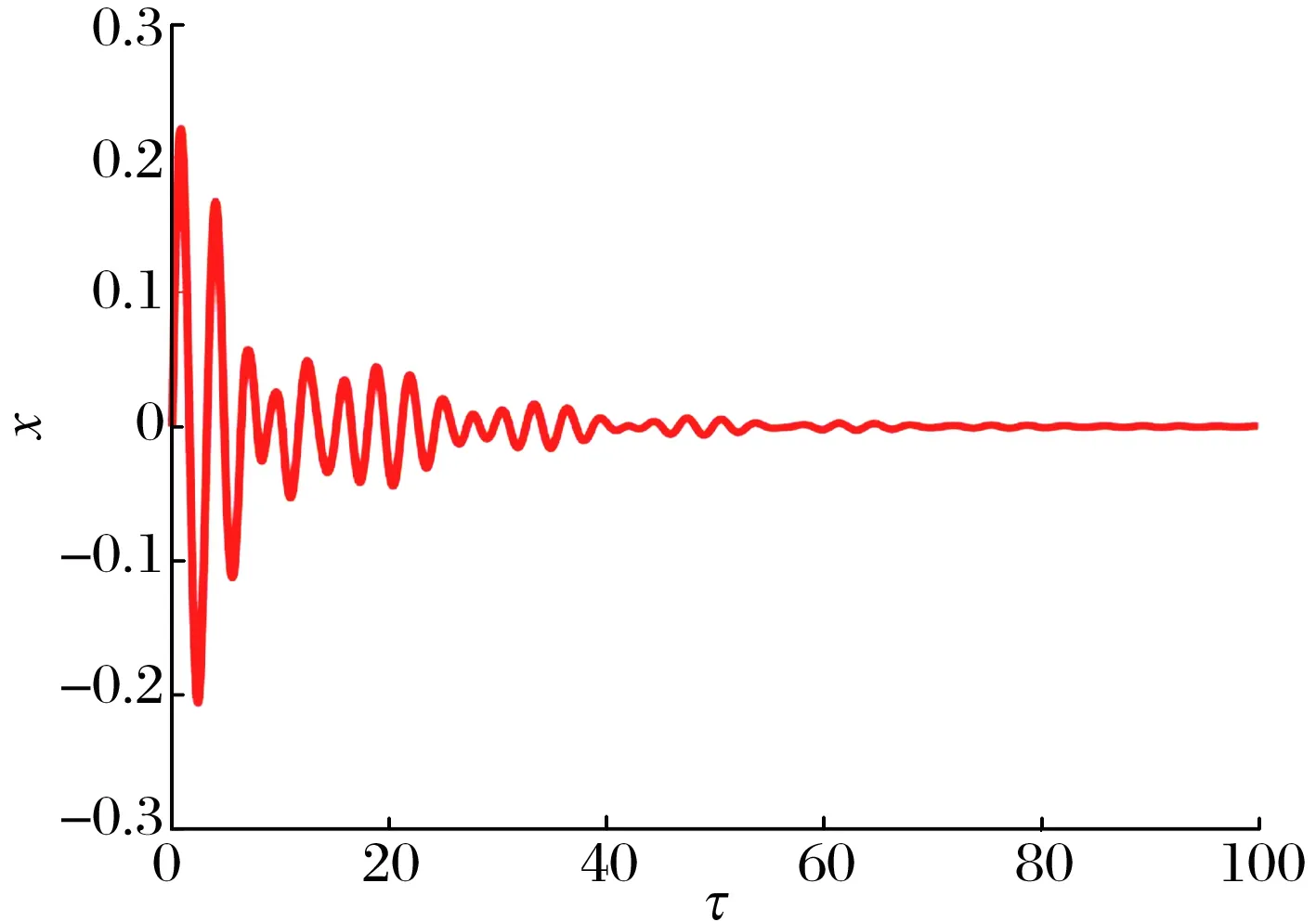
为对比分析BNES与NES在相同工况下的减振效果，取相同系统参数和初始条件，分析NES作用时主系统和NES的振动情况，结果如图7所示。由图可知，对同一系统，在相同激励条件下，NES对主系统有一定减振作用，系统部分振动能量在NES中消耗，但由小波图可知，主系统在τ=60附近仍有较大能量，因此BNES的减振效果更好。

(a)主系统的时域图

3.2 稳态减振性能分析

利用四阶龙格库塔法，在谐波激励下对BNES进行稳态性能分析。分析中系统参数与之前保持一致，激励为F(t)=0.1cos(1.5τ)，初始条件为x(0)=y(0)=x′(0)=y′(0)=0，仿真结果如图8所示。同时，为对比BNES和NES的减振效果，相同条件下分析NES作用时的运动情况，结果如图9所示。BNES及NES在相同系统参数及外界激励条件下与主系统的相对速度关系如图10所示。

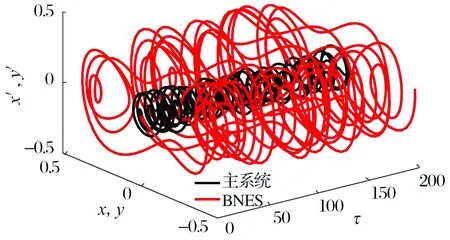
图8 BNES减振性能

图9 NES减振性能

图10 BNES及NES在相同系统参数及外界激励条件下与主系统的相对速度

对比图8和图9可知，在相同系统参数及外界激励条件下，BNES振动幅度远远大于NES；由图10可知，BNES与主系统相对速度极值约为NES与主系统相对速度极值的3.2倍。因为能量阱消耗能量P正比于能量阱与主系统的相对速度Δv的平方[13]，而BNES与主系统相对运动剧烈，可保证能量通过能量阱阻尼耗散。

4 BNES触发阈值分析

基于能量传递率分析BNES在谐波激励下的触发阈值，系统参数仍保持不变，激励为F(t)=fcos(2τ)，初始条件为x(0)=y(0)=x′(0)=y′(0)=0。定义能量传递率为[7]

T(τ)={μx′2(τ)+k1[x(τ)-y(τ)]2+

(13)

式中：T(τ)为BNES在不同时刻存储的总瞬态动能及势能与系统瞬态总能量的比值。

分析不同激励幅值f下BNES的能量传递率，结果如图11所示:在谐波激励幅值f=0.25时，系统能量传递至BNES的不足2%，绝大部分能量仍在主系统里被阻尼消耗；而在激励幅值为f=0.30时，主系统传至BNES的能量接近90%，大部分能量在BNES消耗。

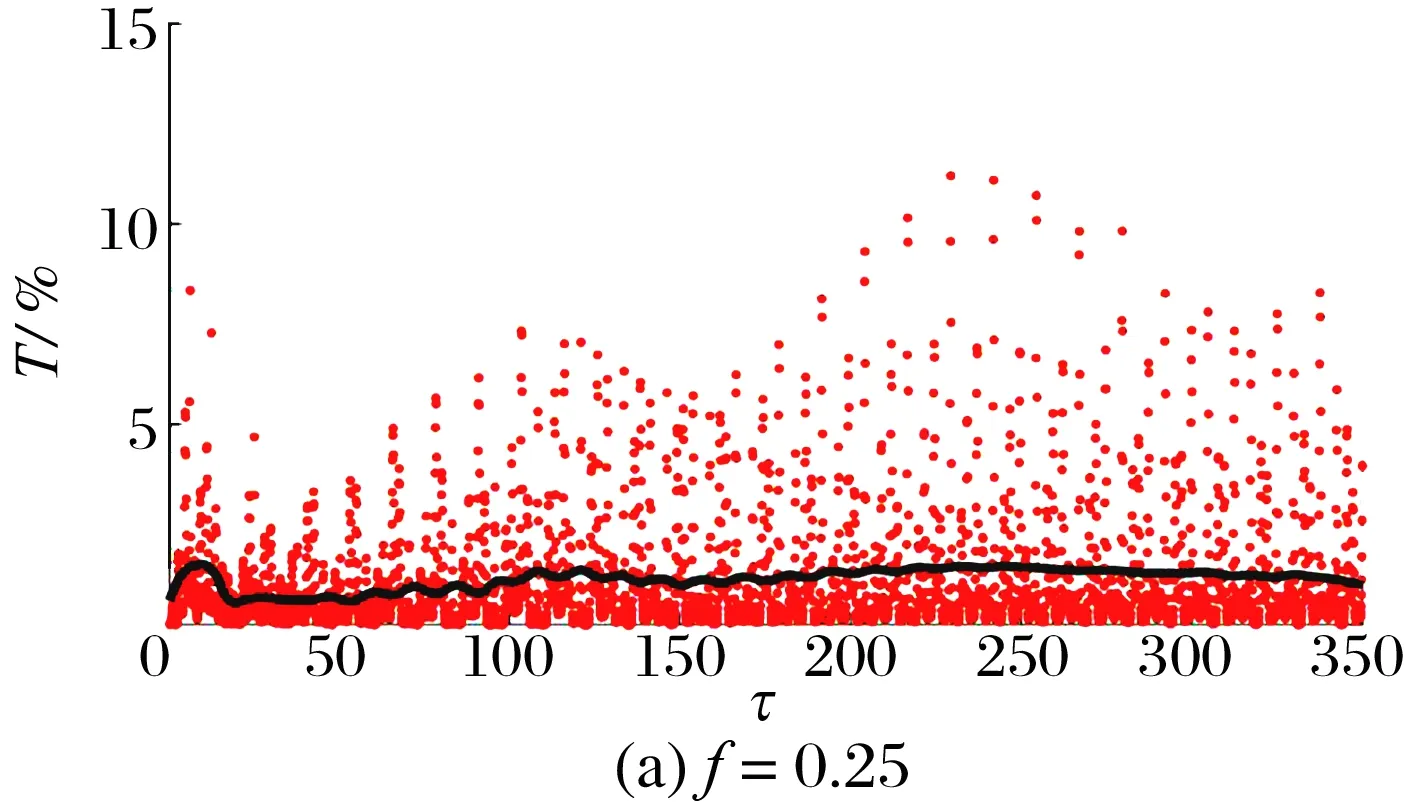
图 11 不同激励强度下BNES的能量传递率

不同激励强度下能量传递率的Colormap图如图12所示，非线性能量阱的触发阈值为0.29，当谐波激励幅值不小于0.29时，BNES发生共振俘获，实现高效减振。

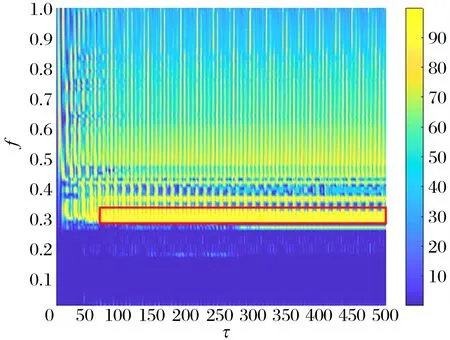
图12 BNES能量传递率Colormap图

此外，由图12可知在非线性刚度比一定时，当激励强度超过阈值后，随着激励的进一步增加，能量传递率相应降低。进一步做如下定义[7]

(14)

式中：En(τ)为各时刻能量阱的能量耗散率；En为稳定后能量阱的能量耗散占比；p为冲击作用下轴的初速度，冲击下系统总能量可表示为E=p2/2。

由(14)式可得不同非线性刚度比下BNES的能量耗散率，如图13所示；随着非线性刚度比的增加，触发阈值降低，但随着轴的初速度(激励强度)增加，能量耗散率降低；非线性刚度比较小时，触发阈值较大，但随轴的初速度(激励强度)增加，能量耗散率可保持在较高水平。

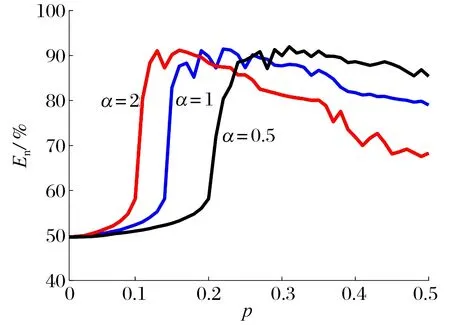
图13 非线性刚度比对触发阈值影响

5 结论

利用线性刚度元件，通过几何非线性构建了BNES，得到以下结论：

1)通过劳斯-赫尔维茨法则，对平衡点进行稳定性分析，发现BNES存在1个不稳定平衡点和2个稳定平衡点。

2)通过数值方法分析了BNES的工作性能，发现相比于普通NES，BNES在低扰动下减振性能更好，更适合高精仪器低扰动下的振动控制。

3)利用能量传递率及能量耗散率分析了BNES的触发阈值，发现触发阈值与非线性刚度比存在反比例关系，在触发阈值附近BNES能量传递率及能量耗散率最高，之后随着激励强度的增加，两者逐渐降低。