采用有效邻近点和适应密度的密度聚类算法
闫强强,张 敏,荀亚玲
(太原科技大学 计算机科学与技术学院,山西 太原 030024)
0 引 言
聚类分析是根据对象之间的相似性,将数据集划分为若干类簇,使类内对象具有高度相似性,而类间对象具有差异性的类簇[1-2],并已成功应用于故障检测、异常值检测、模式识别以及信息检索等领域[3-6]。聚类分析主要分为基于划分的聚类[7-8]、基于层次的聚类[9]、基于密度的聚类[10]和基于子空间的聚类[11]等方法。由于基于密度的聚类分析方法具有不需要提前预估簇类数量,可以发现任意形状的类簇和识别噪声点等优点,已成为聚类分析中的研究热点之一。
密度聚类是一类重要的聚类分析方法,利用数据集中数据对象的邻域密度信息,不需要预先估计类簇数目,就可以发现任意形状的类簇,但随着数据维度的增加,不同类簇之间密度的差异也随之增大,会使聚类效果变差[12];在大多数密度聚类分析中,近邻K值的选取对聚类效果影响极大。该文采用邻近点信息刻画数据对象邻近点的疏密程度,提出了一种基于有效邻近点和适应密度分布的密度聚类算法,并利用数据对象邻近点的相对距离来计算伸缩半径,判断数据对象的有效邻近点,有效减少了对数据对象密度影响较小邻近点的计算,改善了类簇密度分布不均匀、类簇间距离过大导致聚类效果差的问题。
其主要贡献如下:
(1)利用相对距离,定义了有效邻近点;
(2)提出了一种调整簇内有效距离的策略;
(3)提出了一种基于有效近邻点和适应密度分布的密度聚类分析算法。
1 相关工作
密度聚类是依据数据对象的密度进行划分,当一个区域内数据对象的密度大于某个阈值时,将数据对象添加到相近的聚类簇中的聚类。密度聚类分析主要分为两个研究方向:DBSCAN(density-based spatial clustering of application with noise)算法和DPC算法(clustering by fast search and find of density peaks)[13]。DBSCAN利用数据对象的密度信息,计算核心点和边界点实现聚类任务[14],因其具有聚类效率高,对不规则的数据集有良好的聚类效果等优点,已吸引了众多学者关注[15]。
DBSCAN作为一类有效的密度聚类分析方法,其典型研究成果有:周水庚等人提出了一种基于数据分区的聚类算法PDBSCAN[16],该算法依据数据集的分布特性,将整个数据集分为若干个区域,分别对不同区域进行聚类,但聚类效果仍受到邻域半径Eps的影响;Wu Y等人提出了一种基于LSH的线性DBSCAN算法[17],该算法构建LSH(局部敏感哈希)来优化最近邻域搜索过程,聚类效率得到改善,但数据集的聚类效果没有提升,并且在大型数据集上聚类效果不佳;武佳薇提出了一种邻域平衡密度聚类算法bDBSCAN[18],该算法利用核心对象的邻域平衡性,将平衡密度可达的对象划分到同一簇完成聚类,有效排除边界稀疏对象的噪声点,提高了聚类精度,但算法新引入两个参数,在聚类前需要对参数进行多次调整;Cassisi C等人提出了一种增强基于密度的聚类算法IS-DBSCAN[19],该算法利用数据对象的反向最近邻,执行密度聚类,从而有效识别不同密度的类簇;Kumar等人提出了一种通过Groups加速邻居搜索的快速DBSCAN聚类算法[20],该算法有效提高了对大型数据集的计算效率,但聚类效果受参数Eps和MinPts影响较大;于彦伟等人提出一种面对位置大数据的快速密度聚类算法CBSCAN[21],该算法通过确定核心点和密度相连关系,减少了高密度区域的距离计算,提高了聚类效果;Lv Y等人提出一种新的基于影响空间和边界点检测的密度聚类算法(ISB-DBSCAN)[22],该算法改进局部敏感哈希方法,实现了最近邻的快速查找,有效实现区分边界对象和噪声对象;Bryant等人提出一种基于密度的反向最近邻密度聚类算法(RNN-DBSCAN)[23],该算法仅使用参数K实现对不同密度类簇的区分,但是与IS-DBSCAN、ISB-DBSCNA算法相同,聚类效果受近邻值K影响较大;Gholizadeh等人提出一种改进的大数据密度聚类算法K-DBSCAN[24],该算法通过对数据集进行划分聚类,降低DBSCAN执行的计算负担,使算法可以有效地对大数据集进行聚类分析,但此算法的聚类精度没有发生改变。
但上述算法对存在密度有较大差异的数据集进行聚类分析时,参数邻域半径Eps和最小包含点MinPts无法自动适应数据对象密度变换,影响聚类分析效果;且在K近邻与密度聚类相结合的算法中,由于近邻数K影响数据对象的密度,导致聚类效果对K的抗干扰性较差。
针对上述不足,利用相对距离计算数据对象的有效邻近点,有效解决聚类效果受近邻K影响的情况,并通过调整簇内有效距离的策略来适应数据对象密度的变换。
2 密度聚类与核心点
密度聚类分析具有抗噪性强、效率高,以及可发现任意形状的类簇等优点,已得到广泛应用。参照文献[14],相关概念和公式描述如下:
对于给定任意数据集DB={x1,x2,…,xn},其中,n表示数据对象的数量。
以数据对象xi为中心,Eps为半径的区域内包含的数据对象,定义为Eps邻域Neps(xi),如公式(1)所示:
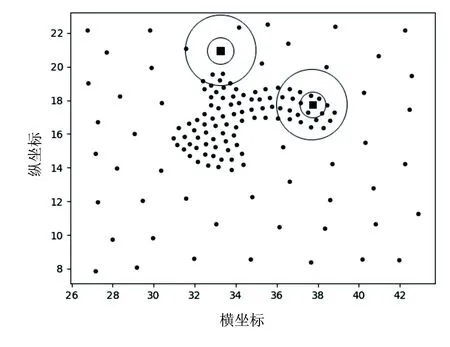
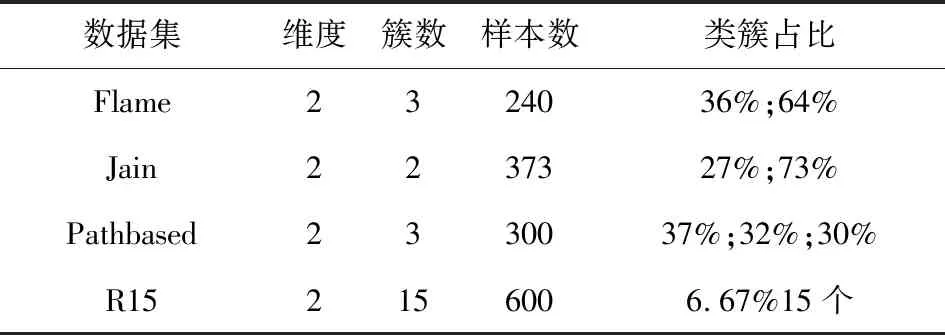
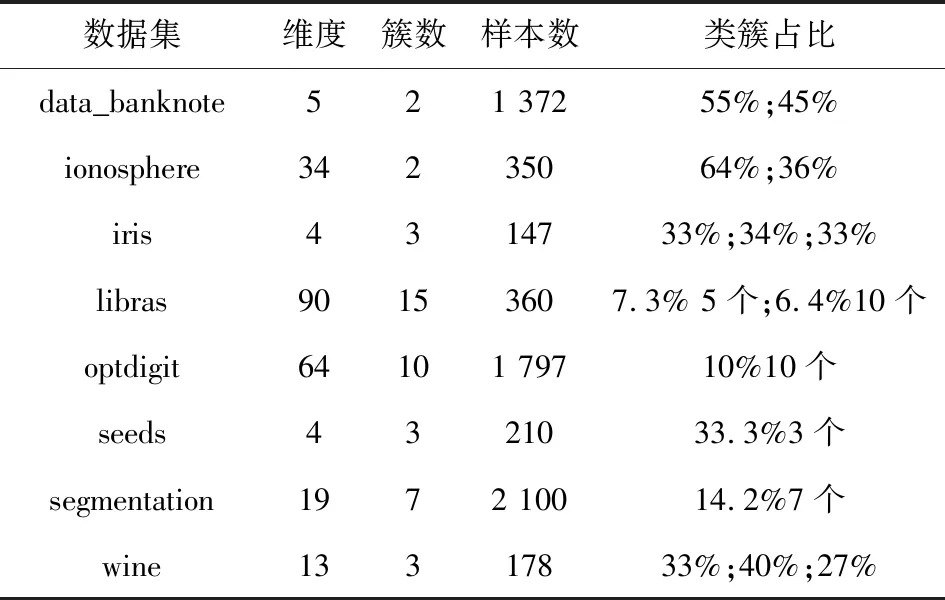
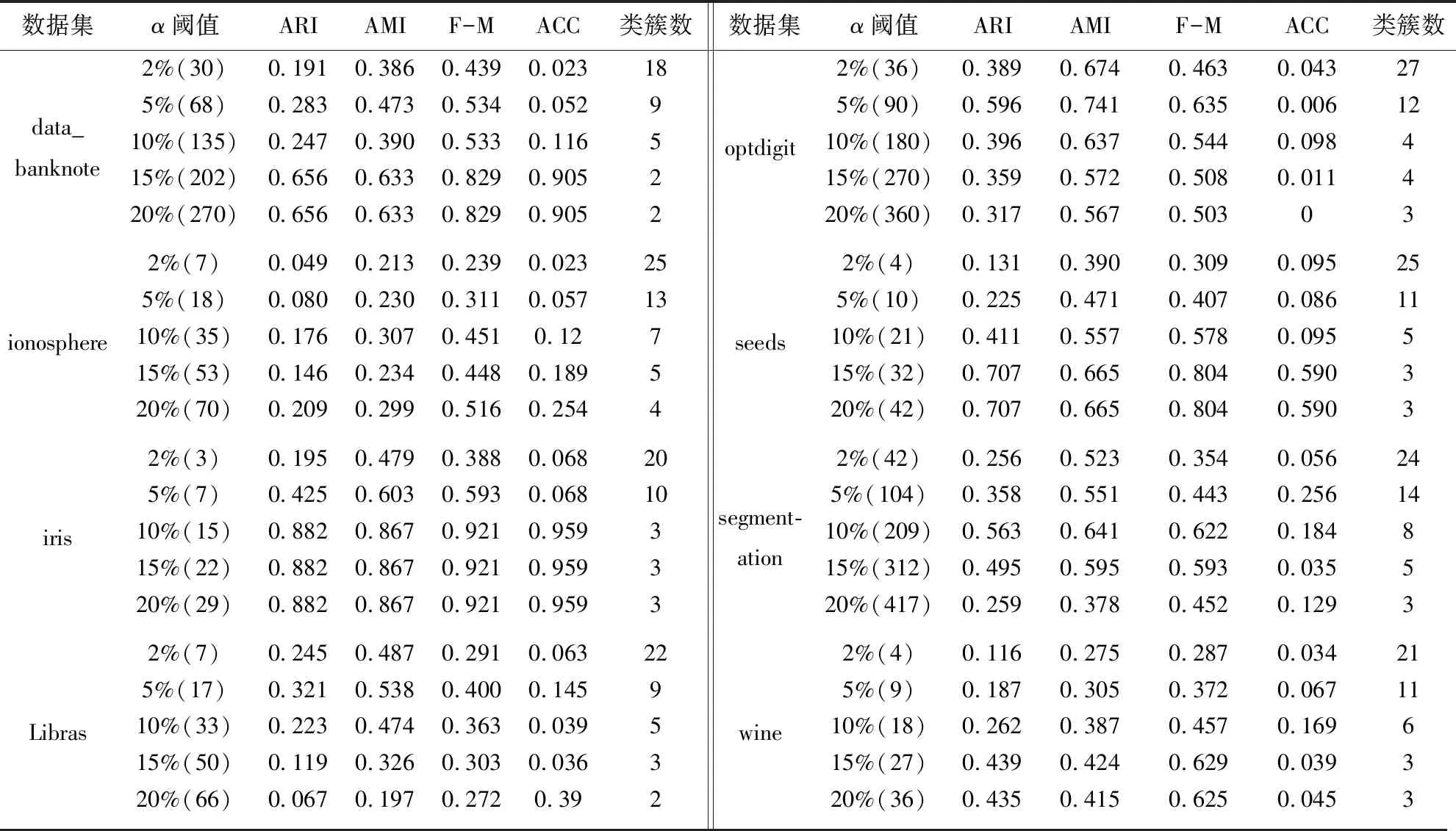
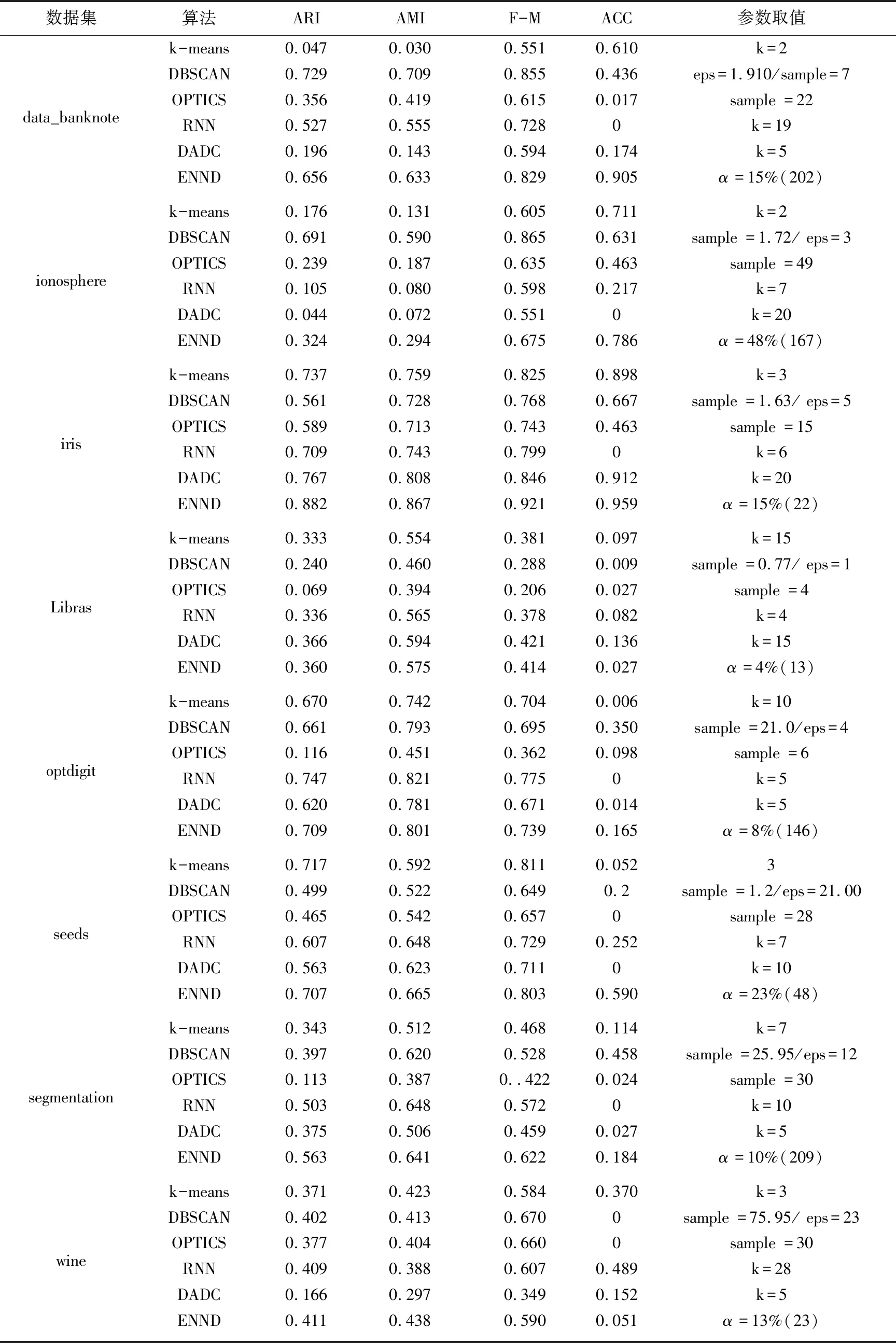
Neps(xi)={xj|dist(xi,xj) (1) 其中,dist(xi,xj)为数据对象xi和xj之间的欧氏距离,xj为数据集中的数据对象。 当数据对象xi在邻域半径Eps内的密度值Num满足公式(2)时,则称数据对象xi为核心点。其中Num为数据对象xi在Eps邻域内数据对象的个数: Num≥MinPts (2) 当数据对象xi的密度值Num不满足公式(2),但其邻域内至少有一核心点时,则称数据对象xi为边界点。 对于任意数据对象xi∈DB,xi的邻近点集N(xi)可定义如下: N(xi)={data1,data2,…} (3) 其中,data1,data2,…分别为数据对象xi的最邻近点,次邻近点,…,其欧氏距离分别表示为d1,d2,…,且按从小到大排序。 数据对象xi的邻近点与最邻近点相对距离σ21,可定义如下: σj1=d(xi,dataj)/d(xi,data1) (4) 其中,j=2,3,…,n;xi为数据对象,dataj为数据对象xi的第j个邻近点,data1为数据对象xi的最邻近点。 在密度聚类的过程中,通常选取邻域半径Eps或数据对象K个近邻点的方式计算数据对象的密度。在图1所示数据集中,类簇中数据对象的邻近点距离存在较大差异。Eps选取定长的方式计算数据对象密度,但Eps无法适应同时存在稀疏类簇和稠密类簇数据集中数据对象近邻点间距的变化,在图1中选取两个数据对象,无论Eps取何值,均无法同时计算数据对象的密度;近邻值K给定确定近邻点个数的方式计算数据对象密度,但并非所有近邻点都对数据对象密度有较大的影响,当选取5作为近邻值K对密度进行密度分析时,稀疏区域中的数据对象有3个近邻点在其他类簇中,且邻近点距数据对象越远,对密度的影响越小。利用Eps或近邻值K均无法准确对类簇中密度差异较大的数据对象进行计算。 因此,可采用伸缩半径适应在同一类簇和不同类簇中数据对象的密度,伸缩半径依据数据对象邻近点特性的计算,无需人为指定或通过数据集判断,具备伸缩性,可有效避免Eps或近邻值K无法同时适应密度差异较大数据集的情况。 为判断数据对象的伸缩半径,可利用相对距离判断数据对象邻近点的距离关系,相对距离是不同数据对象相较于参考点的绝对距离,不因数据对象邻近点距离差异而改变。在不同数据对象的邻近点中,对密度的影响随着距离的增大而降低,其中,最邻近点、次邻近点对数据对象密度影响最大。为判断对数据对象密度影响最大邻近点的相对距离,选取最邻近点作为参考点,计算数据对象次邻近点与最邻近点的相对距离σ21。图2展示了图1所示数据集中相对距离σ21的分布。由图2可知,尽管不同类簇中数据对象邻近点距离有较大差异,但其相对距离σ21存在较高的相似度,在邻近点距离分布较大数据对象中相对距离σ21多分布于1.0、1.1、1.2,不因数据对象邻近点距离而改变,可以较好表示对数据对象密度影响最大邻近点的相对距离。 图1 二维数据集 图2 相对距离分布 因最邻近点对数据对象密度影响最大,将最邻近点距离作为伸缩半径的基长,与相对距离σ21相结合即为数据对象的伸缩半径,数据对象邻近点的距离随着最邻近点距离而改变,使伸缩半径具有伸缩性,可以适应不同数据对象邻近点间距离的改变。利用伸缩半径,克服无法识别数据集中存在密度分布不均匀数据对象的情况。最邻近点为对密度影响最大的邻近点,以最邻近点的距离为基长,在伸缩半径范围内的邻近点与最邻近点对数据对象密度的影响相近,即伸缩半径范围内邻近点均对数据对象密度有较大影响,将伸缩半径范围内的邻近点定义为数据点对象xi有效邻近点ENN(xi)。 取σ21小数点后一位,以最邻近点的距离为基长,当σ21为1.0,对数据对象密度影响较大邻近点的距离仅为最邻近点距离,不能有效判断邻近点中对数据对象密度影响较大的邻近点,故不考虑σ21为1.0的相对距离。为统一判断数据集中数据对象的有效邻近点,选取多次重复出现σ21的中位数作为判断有效邻近点标准∂,选取∂可以有效体现数据集中对多数数据对象密度影响较大邻近点的相对距离,可以有效适应不同类簇中对数据对象密度影响较大邻近点距离的差异,有效邻近点ENN(xi)定义如下: ENN(xi)={dataj|dj<∂×d1} (5) 其中,d1为与xi最近的欧氏距离值,dj为xi第j个最近的欧氏距离值,dataj为xi的第j个邻近点。 位于类簇中心的数据对象,有效邻近点较多,位于类簇边缘的数据对象,有效邻近点较少,利用ENN(xi)的个数判断数据集中的核心点与边界点,当数据对象xi的有效邻近点满足公式(6)时,即可判定数据对象为核心点,核心点定义如下: |ENN(xi)|≥corethreshold (6) 其中,corethreshold为核心点阈值。 当数据对象xi的有效邻近点满足公式(7)时,即可判定数据对象为边界点,边界点定义如下: |ENN(xi)|≥borderthreshold (7) 其中,|ENN(xi)|为数据对象xi的有效邻近点个数,borderthreshold为边界点阈值,其计算方法由算法CalculateIndex给出。 数据对象xi的有效距离EDist(xi)为xi有效邻近点的平均距离,可定义如下: (8) 其中,|ENN(xi)|为数据对象xi有效邻近点的个数,dataj为xi的第j有效邻近点。 类簇中数据对象的密度仍存在差异,为适应类簇中数据对象密度变换,通过调整簇内有效距离的策略对有效距离进行调整。EDist(xi)为xi有效邻近点的平均距离,其中有效邻近点均为对xi密度影响较大的邻近点,若其邻近点在EDist(xi)条件下仍存在有效邻近点,则说明其有效邻近点与数据对象xi的有效邻近点相似。依次遍历xi邻近点中存在有效邻近点的数据对象,分别计算其有效邻近点,将其存放于集合C中,簇内有效距离C_Dist调整如式(9)所示: (9) 其中,|C|为存在有效邻近点数据对象的个数,其有效邻近点的判定为: ENN(xi)={dataj|dj<∂×EDist(xi)} 在对簇进行扩展时,类簇中数据对象xi的有效邻近点的判定如式(10)所示: CENN(xi)={dataj|dj<∂×C_Dist} (10) 其中,C_Dist为簇内有效距离,dataj为xi的第j个有效邻近点,dj为与xi第j个最近的欧氏距离值。 利用簇内有效距离判断数据对象的有效邻近点并对其扩展过程中会出现将单个类簇划分为多个小类簇的情况。对此,算法引入簇对象阈值α对类簇划分进行约束,当数据对象扩展完成后,若扩展的类簇在数据集中所占比例低于α,则不判定类簇的划分。α是根据类簇在数据集中数据对象所占比例决定。 综上所述,基于有效邻近点和适应密度分布的密度聚类分析基本思想为:构建KD树,利用公式(4),选取判断有效邻近点的标准∂,通过公式(5)判断数据对象的有效邻近点;利用公式(6)、(7)完成对数据集中核心点和边界点的判断;利用公式(9)调整簇内有效距离,适应类簇扩展过程中数据对象的密度变换。其伪代码描述如下: 算法:ENND(A density clustering algorithm based on effective nearest neighbor distribution) 输入:数据集DB,簇对象阈值α 输出:聚类结果clustering 1.利用KD树,计算数据对象xi最邻近的距离,从小到大对数据集重新排序 2.∀x∈D:x=Unassign//添加未聚类标签 3. CalculateIndex(D,∂,corethreshold,borderthreshold) 4.fori=1 to |D| { 5.ifxi=Unassign Then 6. ExpandCluster(∂,xi,corethreshold,borderthreshold,cluster) 7.if the number of cluster>α* |DB| Then { 8. cluster=assign}//保存类簇cluster 9. else{cluster = assigned}//标记未聚类数据对象 10. AssignData(assigned,cluster,clustering) 11.return clustering 12.end ENND CalculateIndex算法利用数据对象的相对距离计算数据集的∂、核心点阈值corethreshold以及边界点阈值borderthreshold。 算法1:CalculateIndex(D,∂,corethreshold,borderthreshold) 输入:数据集D 输出:∂,核心区阈值corethreshold,边界区阈值borderthreshold 1.fori=1 to |D|{ 2. calculateσforxi//(σ取小数点后一位) 3. calculate the number of{σ1= =σ21}(k=1,2,…)= core 4. calculate the number of{only bigger than borderσ21}(k=1,2,…)} 5.calculate the median of the two numbers thatσ21most frequently for ∂ 6.borderthreshold = the count max of border 7.corethreshold = count max of core and corethreshold≥borderthreshold 8.if corethreshold isn’t exist then corethreshold = borderthreshold 9.return ∂,borderthreshold,corethreshold ExpandCluster算法利用CalculateIndex算法中∂、corethreshold、borderthreshold,判断核心点和边界点,将未聚类的数据对象扩展为类簇。 算法2:ExpandCluster(xi,∂,corethreshold,borderthreshold,cluster) 输入:数据对象xi,∂,核心区阈值corethreshold,边界区阈值borderthreshold 输出:类簇cluster 1. calculate EDist(xi)//计算数据对象xi有效距离 2.initialize empty list for stack andC 3. putxiin stack 4. while stack is not empty{ 5.xj= stack.pop() 6. calculateENN(xi) ENN(xi)={dataj|dj<∂×EDist(xi)} 7. if {ENN(xj)exist ENN }Then{put ENN(xj) in stack and |C|} 8. calculate C_Dist in|C|//利用集合C中数据对象计算簇内有效距离 9. fork= 1 to |C| { 10. count=the number of CENN(xk) 11.if count ≥corethreshold Then {putxkinto corearea } 12.else {if count ≥ borderthreshold Then {putxkinto borderarea } } 13.clust=corearea+borderarea//将corearea和borderarea的数据对象聚和为类簇cluster 14.return cluster AssignData算法对未聚类成功的数据对象进行二次分配,依次判断数据对象邻近点的归属,将数据对象划分给邻近点归属的类簇。 算法3:AssignData(assigned,cluster,clustering) 输入:未聚类数据对象assigned ,类簇cluster 输出:类簇clustering 1.while True 2.forj=1 to |assigned|{ 3.fori=1 tok(k=1){ 4.if{ 5.assigned[j] the dataiis in cluster 6. assigned[j]=cluster(datai)//若数据对象assigned[j]的第i邻近点被分配,则xj划分到第i邻近点的类簇中 }} 7.if exist assigned{k=k+1 continue } 8.else break } 9.将所有簇类合并为聚类结果clustering 10.return clustering 算法复杂性分析:在ENND算法中,计算数据集的邻近点,其时间复杂度为O(nlogN),计算核心点和边界点阈值的时间复杂度为O(n);对数据集中所有数据对象进行扩展,其时间复杂度为O(n2);对未分配的数据对象进行二次分配,其时间复杂度为O(n)。因此,ENND算法的时间复杂度为O(knlogN+n+n2+n)≈O(n2)。由于在数据对象的扩展过程中,只针对数据对象的有效邻近点进行扩展,时间复杂度应远小于O(n2)。 实验环境:Windows OS10系统,Intel(R)Core(TM)i5CPU,16 GB动态随机存取存储器和1 TB主内存。实验数据来源于人工数据集(https://cs.joensuu.fi/sipu/datasets/)和UCI数据库(http://archive.ics.uci.edu/ml/index.php),其详细描述见表1和表2。聚类效果评价指标:调整兰德指数(ARI)、归一化信息(NMI)、Fowlkes-Mallows(F-M)、精度(ACC)[25]。采用K-means[26]、DBSCAN[12]、OPTICS[27]、RNNDBSCAN[23]、DADC[28]作为ENND的实验对比算法。类簇占比均采用四舍五入。 表1 人工数据集 表2 UCI数据集 设数据集DB含有n个数据对象,m个属性维度,对于任意数据对象x,y,采用欧氏距离来表示数据对象x和y之间的距离。在对数据集进行处理时,删除相同数据对象。 为验证簇对象阈值α对聚类效果的影响,分别选取2%,5%,10%,15%,20%作为UCI数据集的α,将调整兰德指数、归一化信息、Fowlkes-Mallows和精度作为评价指标,其实验结果如表3所示。 由表3可以看到,ENND聚类效果与类簇在数据集中占比及数据集的分布特征密切相关。当类簇占比分布均匀时(例如:iris、optdigit、seeds数据集),α值越大,聚类效果越好,其主要原因是当α值增加,ENND利用有效邻近点对簇内有效距离的调整,有效地适应于类簇中数据对象的密度变换,从而判断类簇中的核心点和边界点;当类簇占比分布不均匀时(例如:data_banknote、ionosphere、Libras、wine数据集),α值越小,聚类效果也随之变差,其主要原因是较小的簇内有效距离仅能识别类簇中部分核心点与边界点,α减少会导致核心点与边界点满足聚类条件(α),从而将单个类簇划分为多个小类簇,聚类效果变差;当α值大于最小类簇占比时(例如segmentation数据集),聚类效果变差,其主要原因是α大于最小类簇占比时,类簇中由核心区域内的数据对象扩展的类簇无法满足聚类条件,而对边界区域内的数据对象扩展时,得到较大的簇内有效距离,会将非本类簇中的数据对象错误识别,导致聚类效果变差。 表3 α对聚类效果的影响 综上所述,对于多数UCI数据集,当簇对象阈值α未大于最小类簇占比时,聚类效果随α的增大而增加,在接近最小簇占比及大于最小簇占比时,聚类效果变差。 为实验验证ENND对不同密度、不同形状类簇的聚类效果,采用了如表1所示的4个人工数据集。由4.1节可知,当簇对象阈值α小于最小类簇占比时,聚类效果较好,flame、jain、pathbased均为类簇占比不均匀数据集,选取α为20%;R15类簇占比分布均匀数据集,分别选取α为5%。为得到其他算法最好的聚类效果,依据文献[25]中调整参数方法对K-means、DBSCAN、OPTICS参数选取,针对RNN-DBSCAN、DADC,采用改变近邻K取值的方式选取参数。其实验结果见图3~图6。 在图3中,Flame数据集是由两个形状不规则的类簇构成,除K-means算法外,其他5种算法均可正确识别类簇。在图4中,Jain数据集是由两个密度差异较大双月形状的类簇构成,K-means算法错误地将类簇分为两类,其他聚类算法可以很好地识别密度分布不均匀的类簇。在图5中,Pathbased数据集中相邻的类簇间存在交叉数据对象,K-means算法无法识别非凸状的数据集,DADC算法由于聚类融合度(CFD),无法正确合并类簇,其他4种算法均可以实现对数据集正确的聚类分析。在图6中,R15数据集类簇具有凸状,6种算法均可正确识别类簇。 图3 6种算法在FLame数据集的聚类结果 图4 6种算法在Jain数据集的聚类结果 图5 6种算法在Pathbased数据集的聚类结果 图6 6种算法在R15数据集的聚类结果 综上所述,ENND的聚类结果优于K-means、DADC,与DBSCAN、OPTICS、RNN-DBSCAN的聚类结果基本相同,能够有效地实现对不同密度、不同形状类簇的聚类分析,其主要原因是ENND算法通过有效邻近点的判断,无需考虑数据对象邻近点间距离的差异。 为实验验证ENND聚类性能,采用调整兰德指数、归一化信息、Fowlkes-Mallows和精度指标,以及如表2所示的UCI数据集,依据表3中的聚类效果,选取ENND中的α阈值,依据4.2节中选取参数方式,设置对比算法的参数阈值,其实验结果如表4所示。 从表4中可以看出,ENND的聚类效果在多数情况下,优于5种对比算法。其主要原因是:在高维数据集中,数据对象密度差异较大,参数邻域半径无法适用于整体数据对象,因此DBSCNA、OPTICS的聚类效果较差;RNN-DBSCNA算法通过引入逆K近邻,消除了邻域半径对数据对象密度的影响,但忽视了数据对象近邻点间距离,因此高维数据集的聚类分析效果较差;DADC算法利用域自适应密度寻找密度峰值点,但在高维度数据中,类簇间存在较多交叉点,导致在类簇融合过程中,聚类融合度(CFD)会将部分类簇错误合并,使聚类结果比ENND较差;ENND算法在类簇扩展过程中,利用有效邻近点调整簇内有效距离,使得在高维数据聚类分析中,有效识别类簇中存在密度差异较大的类簇,因此,ENND相较于其他算法,对高维数据具有良好的聚类分析效果,但ENND对ionosphere进行聚类时,因类簇间交叉点较多及邻近点间距离相差较小,最小簇阈值48%聚类效果最好。 表4 6种算法在UCI数据集上的聚类结果 提出了一种基于有效邻近点和适应密度分布的密度聚类算法,通过相对距离计算伸缩半径,判断数据对象的有效邻近点,计算簇内有效距离来适应簇数据对象密度变化,有效解决了在高维数据集中,类簇密度差异较大导致聚类效果差以及聚类效果受近邻K影响较大的问题。但算法在对大数据聚类分析中,聚类效率较差。故为了适应大数据聚类分析任务,在Spark集群环境下,基于有效邻近点和适应密度分布的并行密度聚类分析是下一步研究工作。3 基于有效邻近点和适应密度分布的密度聚类
3.1 有效邻近点及相关定义


3.2 基于有效邻近点和适应密度分布的密度聚类算法
4 实验结果与分析
4.1 簇对象阈值对聚类效果的影响
4.2 聚类簇可视化




4.3 聚类性能分析
5 结束语

