基于密度加权原型网络的小样本学习算法
华 超,刘向阳
(河海大学 理学院,江苏 南京 211100)
0 引 言
随着计算机视觉的发展,深度学习的出现,各种深度网络在处理数据量大的数据集进行图像识别、目标检测、自然语言处理等任务时可以取得较好的结果,但是深度学习为此而付出的成本却比较大。在进行深度学习时,为了得到较好的网络模型参数,需要大量有标签的数据和时间来训练网络,而在现实生活中获取大量有标签的数据成本很大,因此需要研究其他的方法来解决这些问题。人类能够在少许的样本中学习并识别新的对象类别,为了让计算机也具备这种能力,提出了小样本学习。
Wang Yaqing等[1]将小样本学习方法概括为以下三类:第一类是通过先验知识增强数据集,该方法是通过先验知识将少量有标签或无标签的数据集,小样本训练集和相似的数据集转换成足够的训练数据集,例如E. D. Cubuk等提出的从数据中学习增强策略[2],J. Wei等提出的用于提高文本分类任务性能的简单数据增强技术[3]等;第二类是通过先验知识限制假设空间,该方法是通过先验知识将样本假设空间约束到较小的假设空间中来进行学习,从而更快地找到较好的结果,例如Oriol Vinyals等提出的匹配网络[4],Snell J等提出的原型网络[5]和F. Sung等提出的相关网络[6]等;第三类是通过先验知识在假设空间中改变搜索策略,该策略将从相关任务中学习的预训练模型进行较好的初始化,通过几次迭代适应数据集,例如C Finn等提出的与模型无关的快速适应深度网络元学习[7]和与模型无关的概率元学习[8]和L. Bottou等提出的大规模机器学习的优化方法[9]等。
Snell J等提出的原型网络属于第二类,是基于嵌入学习的小样本学习的方法。该方法首先通过卷积神经网络将样本映射到更低维的嵌入空间,然后分别将每个类别的样本均值作为各自的原型,当遇到新样本时,计算该样本到每个原型的距离,最后将该样本判给距离原型最小距离的类别。原型网络算法简单地将每个类别的样本均值作为各自的原型,会带来一些缺点。第一,将每个类的样本均值作为各自的原型,从而忽略样本本身的特性,从而使得原型不具有代表性,在判别新样本属于哪一类别时,很容易产生误差。第二,由于每个类的样本数较少,在计算原型时会有不确定性,当样本中存在离群点时,会使计算的原型偏离真实的原型。为了缓解以上的缺陷,该文对计算原型的方法提出了改进。
对于某一类的样本而言,原型网络算法利用均值计算原型,其本质是对每个样本赋予相同的权值,然后进行加权。而每个样本的代表性是不一样的,因此该文对每个样本赋予不同的权值。首先考虑每个样本在某固定范围内的样本个数是不同的,即样本在某固定范围内的样本个数越多,则该样本的密度越大,即该样本就越具有代表性;而样本在某固定范围内的样本个数越少,则该样本的密度越小,即该样本就越不具有代表性。该文给予代表性大的样本赋予更大的权值,给予代表性小的样本赋予更小的权值。基于上述的策略,提出了密度加权原型网络算法,为了将密度加权的思想更加生动地表示出来,绘制了二维的图像来表示。假设样本点的分布如图1所示,样本点中存在一个偏离总体的样本点,为了减小该样本点对计算原型的影响,首先计算出每个样本点在固定的范围内的样本数,样本点在固定范围内的样本数越多,在图中以样本点为中心的范围标识的颜色越深,则样本点的密集就越大,赋予它较大的权值;而对于离群点,在图中以该样本点为中心的范围标识的颜色越浅,则样本的密集就越小,赋予它较小的权值,利用密度加权计算得到原型更加接近真实的原型,相对于直接计算所有样本点的均值作为原型更优。详细的理论在后面进行说明。
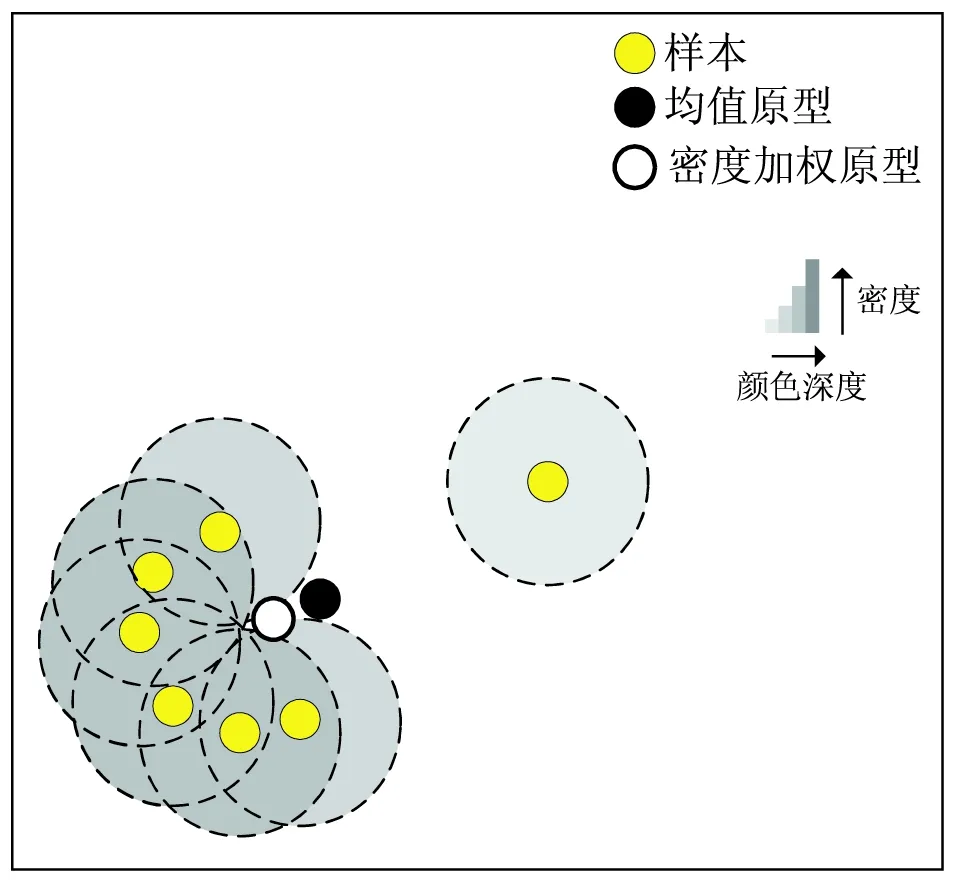
图1 密度加权结构
1 原型网络
1.1 数据集分割
在原型网络算法中定义了情节(episodes)的方式,首先将数据集划分为训练集、验证集和测试集,其中训练集、验证集和测试集的类别不相交,然后对它们进行进一步划分,从中选取N个类别K样本(N-wayK-shot)称为一个情节。从划分好的数据集中抽取N个类别,每个类别中选取m个样本作为支持集S={(x1,y1),…,(xm×N,ym×N)|xi∈RH×W×C,yi∈{1,…,N}},从N个类别中剩余的样本中选取n个样本作为查询集Q={(x1,y1)…(xn×N,yn×N)|xi∈RH×W×C,yi∈{1,…,N}}。
1.2 网络框架
原型网络算法采用的神经网络框架是Vinyals[2]等人构造的。网络框架由四个卷积块组成,每个卷积块包括含有64个3×3卷积核[10]的卷积层、批归一化层、ReLU非线性和2×2最大池化层,如图2所示。
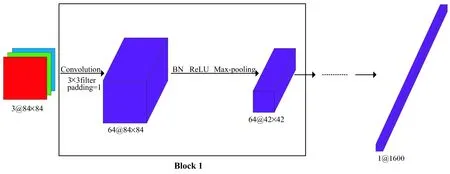
图2 网络框架
1.3 原型的计算
支持集经过网络框架[11]后变为f(S),其中f表示神经网络框架,且f:x→f(x),f(x)∈RD,然后将每个类的均值作为各自的原型。
表达形式如下:
(1)
其中,f(Sk)表示支持集中第k类样本经过网络框架的集合,ck表示第k类的原型。
1.4 损失函数的计算
查询集经过网络框架后变为f(Q),分别计算查询点f(xj)到每个原型的距离,利用softmax生成它到每个类别的概率,那么f(xj)属于第k类的概率可表示为:
(2)
为了最大化p(y=k|f(xj)),需要最小化损失函数J,损失函数表示如下:
J=-log(p(y=k|f(xj)))
(3)
2 密度加权算法
原型网络平等地看待每个类别中的样本,而不考虑样本本身的特性。然而,每个类别中不同的样本在代表性上有差别。为此,该文提出了一种基于密度加权的策略,每个类别中密度较大的样本,它们的代表性越大,赋予它们较大的权重;密度较小的样本它们的代表性越小,赋予它们较小的权重。然后根据每个样本赋予的权重,加权得到原型。该文将利用密度加权算法得到的原型网络称为密度加权原型网络。
在图1中以每个样本为中心在临界距离范围[12]内的样本数不同,如果以样本为中心在临界距离范围内的样本数越大,那么该样本的密度越大,该样本的代表性越强,对应图中的以样本为中心在固定距离范围颜色越深。如果以样本为中心在临界距离范围内的样本数越小,那么该样本的密度越小,该样本的代表性越弱,对应图中的以样本为中心在固定距离范围颜色越浅。每个类别利用密度加权算法计算原型的具体流程如下。
2.1 计算距离矩阵
为了度量每个类别的样本的密度[13],利用距离矩阵来度量各个样本到其他样本的距离,再对距离矩阵进一步处理得到各个样本距离它们相对较近的样本的个数,将得到的每个样本相对较近的样本个数进行归一化,从而得到要求得的权值。距离矩阵具体的数学表达形式如下:
(4)
Dk表示第k类样本的距离矩阵,其中dij=‖f(xi)-f(xj)‖2,易知距离矩阵是一个对角矩阵,且主对角线上的元素全为零。
2.2 计算临界距离

(5)
其中,quantile(dk)表示dk的分位数。
2.3 计算权重
(6)
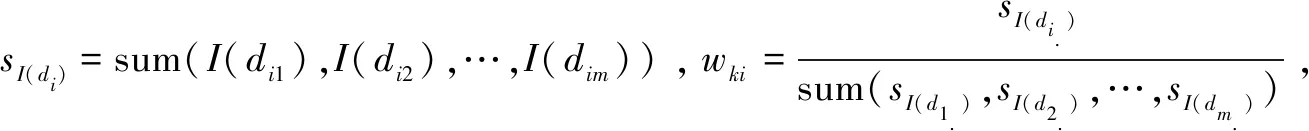
2.4 计算加权原型
利用式(6)第k类样本的权重wk=(wk1,…,wkm)'与第k类样本进行加权来重新计算原型,表达形式如下:
(7)
3 密度加权原型网络算法流程
利用密度加权算法来计算原型分为以下几个步骤,支持集经过网络框架后计算每个类别中各自样本到其他样本之间的距离得到距离矩阵,利用距离集合来构造临界距离,利用0-1函数作用在距离矩阵的每个元素当中,对处理后距离矩阵进行行求和,得到在每个样本在临界距离内的样本数,进行归一化得到相应的权值,利用权值与样本进行加权计算原型。利用计算好的原型和经过网络框架的查询集样本带入到公式(2)和(3)中得到损失函数。具体算法流程如下:
算法1:密度加权原型网络。
输入:训练集Dtrain={(x1,y1),…,(xM,yM)|xi∈RH×W×C,
yi∈{1,…,K}}
输出:训练损失
1.生成支持集S:从训练集中随机抽取N个不同的类别,再从每个类别中抽取m个不同的样本,且N≤K;
2.生成查询集Q:从训练集中随机抽取N个不同的类别,再从每个类别中抽取n个不同的样本,且S∩Q=∅;
3.支持集和查询集样本经过神经网络框架嵌入到特征空间分别表示为:f(S),f(Q);
4. forkin {1,…,N} do
5.第k个类别中样本距离矩阵Dk=(dij)m×m;
7.由公式(6)定义I(x),并通过计算公式(6)计算wk;
9. end for
10.J←0
11. forkin {1,…,N} do
12. for(f(xj),yj) inf(Qk) do
13.通过公式(2)计算p(y=k|f(xj));
14. 通过公式(3)计算J;
15. end for
16. end for
4 实验及结果分析
实验主要对训练和测试过程中得到的结果进行分析。在训练期间保存好每次训练的模型并在验证集上得到相应损失值和准确率,将它们可视化进行分析。在测试期间建立评估指标,分别为准确率的置信区间和平均准确率,准确率的置信区间表示对测试期间episodes得到的准确率的均值的区间估计,平均准确率表示计算前n次迭代的平均准确率。将测试集带入到训练期间得到的最大准确率的模型中,计算每次迭代得到的平均准确率和所有迭代得到的准确率的95%置信区间,对比模型之间的差异。
4.1 实验说明
miniImageNet是来自ImageNet的一个子集,由60 000张大小为84×84的RGB图像组成,分为100个类别,每个类别有600个样本。将整个数据集划分为训练集、验证集和测试集,采用Ravi和Larochelle[2]分割的方法,他们将100个类别进行划分,64个类别用于训练,16个类别用于验证,20个类别用于测试。将每张84×84的RGB图片带入原型网络框架[15]中会输出一张1×1 600的向量,如图2所示。训练网络框架利用随机梯度下降法通过Adam进行优化,将初始学习率设置为0.001,每2 000个episodes将学习率降低一半。并且仅使用批量归一化,没有使用正则化。在训练和验证期间设置了5-way 5-shot和20-way 5-shot,对于5-way 5-shot实验在kaggle网站内置的GPU环境,NVIDIA发布的PCI-E TeslaP100,网络框架在Pytorch1.6.0进行训练,对于20-way 5-shot实验,配置为RTX2080,网络框架在Pytorch1.6.0进行训练
4.2 训练过程结果分析
在训练和验证期间设置了5-way 5-shot和20-way 5-shot,每个类别的查询点的个数为支持点个数的3倍,总共600个episodes。测试期间的episodes和训练时期的一致。临界距离的不同会对加权原型的计算产生很大的影响,经过反复实验比较70%~95%分位数效果较好,该文选取了75%、90%分位数计算临界距离,得到密度加权原型网络[16],结果如图3和图4所示,图中PN,75_PN和90_PN分别表示原型网络算法,90%分位数和75%分位数计算得到的密度加权原型网络算法。可以看出利用90%分位数和75%分位数计算临界距离得到的密度加权网络的损失函数随着迭代次数的增加,总体位于原型网络的损失函数的下方;其准确率随着迭代次数的增加,总体位于原型网络的准确率的上方,所以密度加权原型网络相对于原型网络更优。

图3 5-way 5-shot分类损失曲线

图4 5-way 5-shot分类准确率曲线
4.3 测试过程结果分析
为了进一步与原型网络进行比较,对于5-way 5-shot分类,将测试集带入到训练好的模型进行测试。测试阶段采用的episodes和训练阶段的一样,进行150次迭代,当进行第n次迭代时,计算前n次迭代的平均准确率,结果如图5所示。可见利用90%分位数和75%分位数计算临界距离得到的密度加权原型网络测试的平均准确率比利用简单的均值来计算原型得到原型网络的平均准确率要高;随着迭代次数的增加,密度加权原型网络测试平均准确率明显优于原型网络,当迭代次数大于25时这种趋势比较明显。
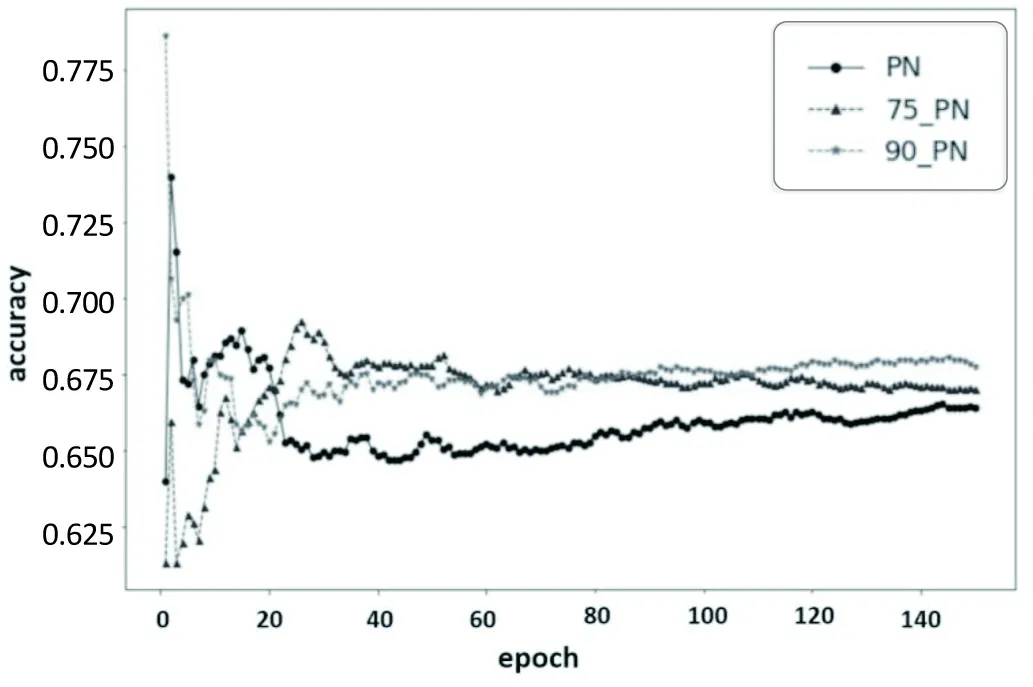
图5 5-way 5-shot分类平均准确率曲线
对于20-way 5-shot分类,随着样本量的提升,准确率也有很大幅度的提升。将测试集带入到训练好的模型进行测试。测试阶段采用的episodes和训练阶段的一样,进行200次迭代,当进行第n次迭代时,计算前n次迭代的平均准确率,结果如图6所示。可见利用90%分位数和75%分位数计算临界距离得到的密度加权原型网络的测试平均准确率比利用简单的均值来计算原型得到原型网络的平均准确率要高;随着迭代次数的增加,密度加权原型网络测试平均准确率明显优于原型网络,当迭代次数大于50时这种趋势比较明显。

图6 20-way 5-shot分类平均准确率曲线
将5-way 5-shot,20-way 5-shot分类实验设置其他的模型性能的评估指标,与原型网络算法进行对比,从测试集中随机生成的200个episodes进行测试,计算每次episode的准确率,并得到200个episodes准确率的95%置信区间,具体结果见表1。由于实验条件和其他因素不一样,该文原型网络的结果与原型网络作者得到的结果存在着一些差异。如表1所示,密度加权原型网络优于原型网络,且利用90%分位数得到的密度加权原型网络比原型网络大约提升1个百分点。

表1 miniImageNet上分类精度
5 结束语
为了减小离群点对原型计算的影响,并在计算原型的过程中充分利用每个样本的特性,提出了原型网络算法的改进方法,在计算原型的方法中采用密度加权算法来计算原型。密度加权算法的思想是对密度大的样本赋予较大的权值,对密度小的样本赋予较小的权值。而对于密度的衡量关键取决于对临界距离的选取。由于不同临界距离内的样本数是不同的,距离越大,每个样本所包含的样本数越多,那么对于一些偏离总体的样本对应的密度相对较小,从而偏离总体的样本对原型的计算影响较小;距离越小每个样本所包含的样本数较少,使得密度的区分相对不明显,原型的计算变化不明显当取分位数最大最小时每个样本的密度一样,从而与利用均值计算原型一致。原型网络算法的核心在于优化网络框架,使得样本经过网络框架后类内的差异更小,类间的差异更大,更容易分类,在今后的工作中为了进一步提升密度加权网络算法的精度,将对损失函数的进行改进来达到这个目的。

