磁液双悬浮轴承单自由度支承系统一阶参数灵敏度分析

李伟楠，杨永，王进，赵建华,2

(1.石家庄海山实业发展总公司,河北石家庄 050200;2.燕山大学，河北省重型机械流体动力传输与控制实验室,河北秦皇岛 066004)

0 前言

磁液双悬浮轴承是一种以电磁悬浮为主、液体静压支承为辅的新型悬浮轴承，包括电磁悬浮及液体静压两支承系统，集磁液两系统的优势于一身，大幅提高了承载能力及刚度，非常适合于中速重载、大承载能力、高运行稳定性的场合及工况。

磁液双悬浮轴承由机架、变速电机、联轴器、阶梯轴、径向轴承、轴向轴承、轴向加载马达和径向加载马达等部件组成，如图1所示。

图1 磁液双悬浮轴承系统

磁液双悬浮轴承的定子周向均布8个磁极，每个磁极均缠绕相同匝数的线圈，如图2—图3所示。由于线圈的缠绕方式，各磁极呈NSSNNSSN方式分布。相邻两磁极与导磁套之间形成磁回路，产生电磁吸引力。每个磁极内部加工有进液孔，磁极端面作为静压支承面，与转子导磁套间存在较小的间隙；当液体流经微小间隙时，形成较大液阻，在磁极端面上建立流体静压力，产生静压支承力。以磁液双悬浮轴承系统竖直方向上单自由度支承系统为例，其调节过程以及受力分别如图4、图5所示。

图2 径向磁液双悬浮轴承实物

图3 磁液双悬浮轴承径向轴承单元剖视图

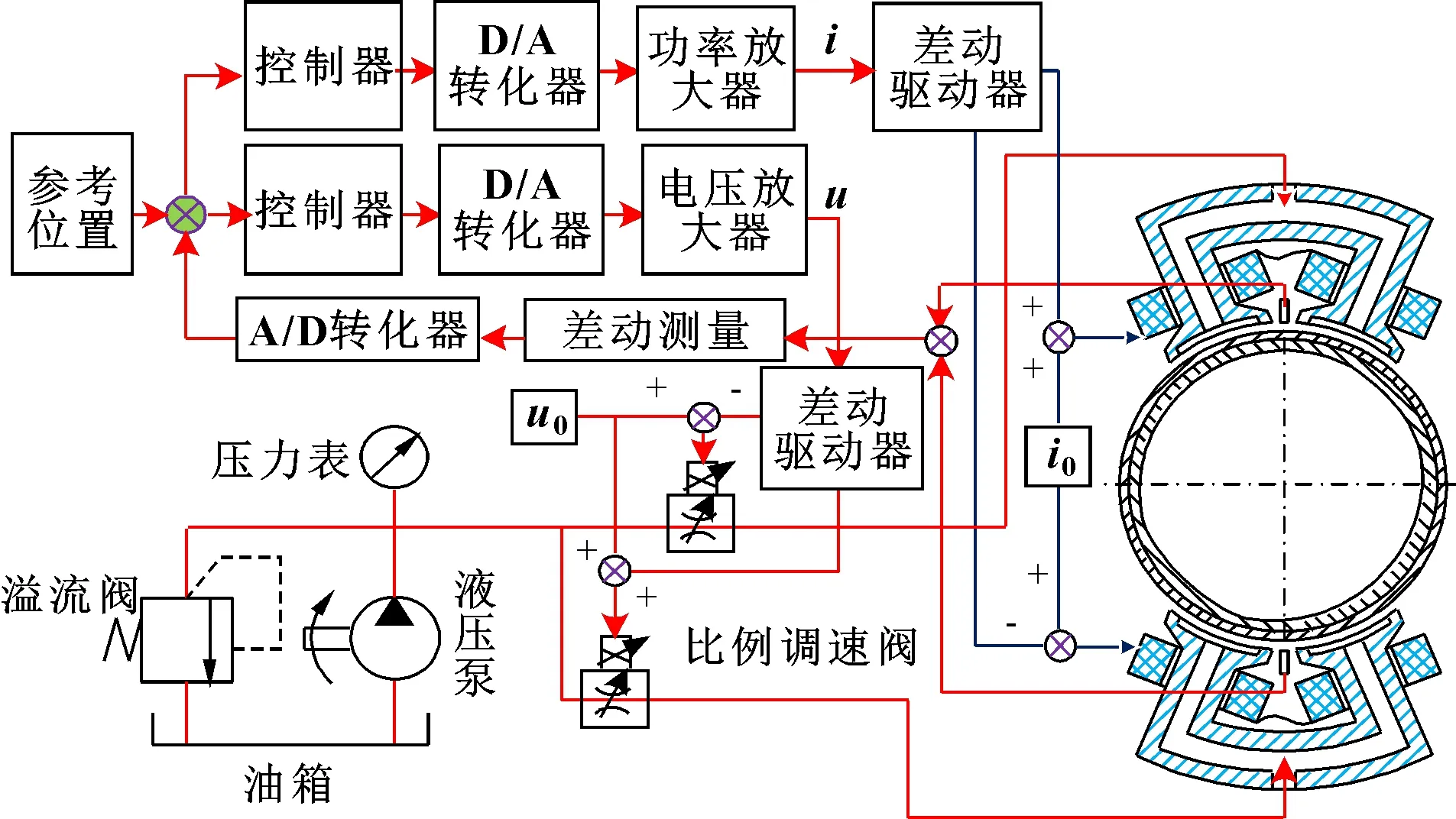
图4 磁液双悬浮轴承单自由度支承系统调节示意

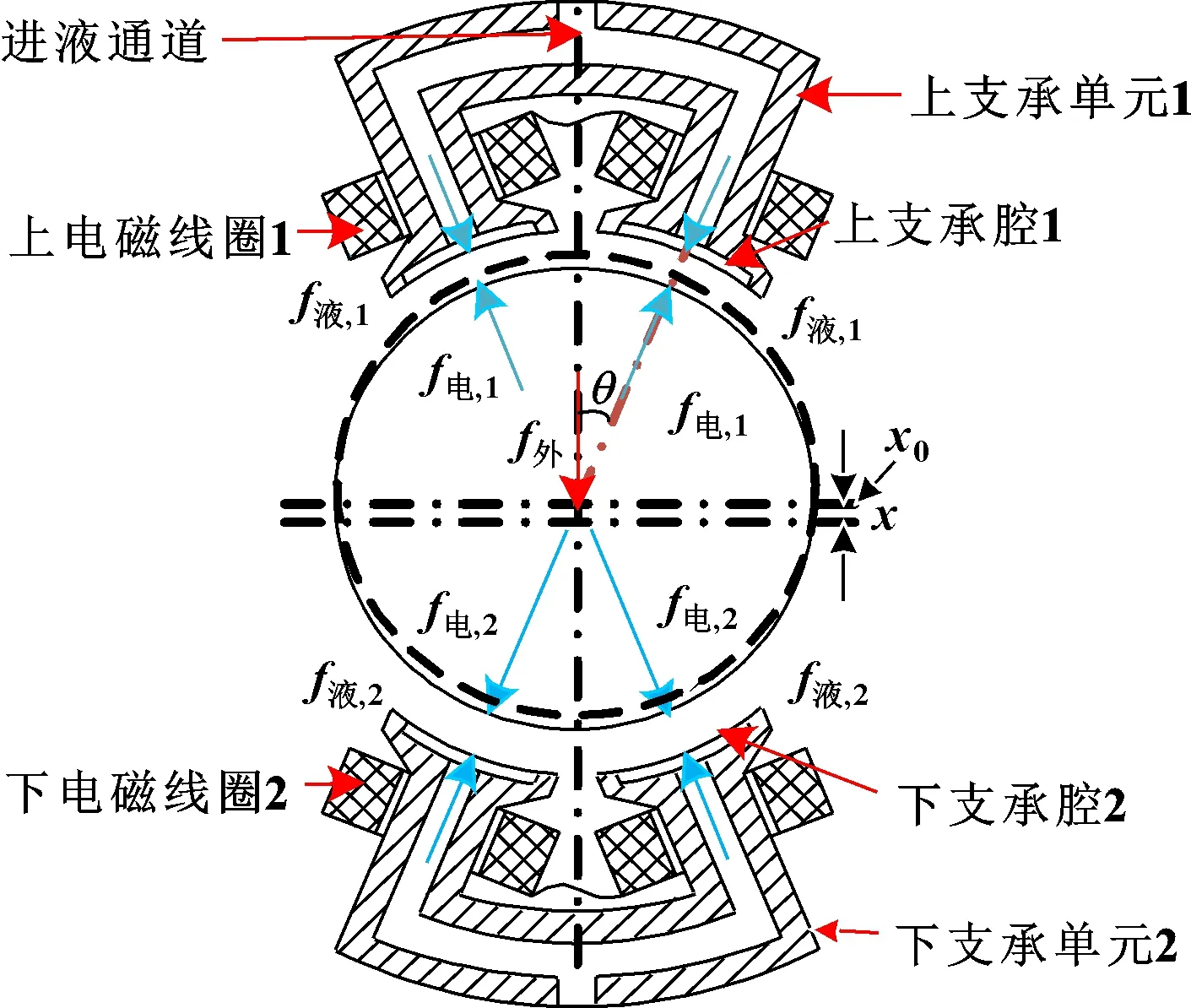
图5 磁液双悬浮轴承单自由度受力示意

轴承系统采用双闭环反馈调节，通过位移传感器实时检测轴承转子位移变化，并将位移偏差信号转化并传递给电压控制器和电流控制器，通过调节比例调速阀偏置电压和电磁线圈电流，进一步调节流量及电流，从而抑制转子悬浮间隙的变化，使磁液双悬浮轴承再次达到平衡状态。初始状态下，上、下电磁线圈偏置电流为且上、下静压支承液膜厚度一致，转子处于回转中心(上下悬浮间隙为30 μm)。当外扰动突然作用于转子，转子位移为，通过控制电流产生向上电磁合力，与此同时，由于转子发生偏移，导致上下支承腔液膜厚度变化，进而产生向上静压支承合力，通过电磁力与静压支承力共同调节，该轴承转子重新回到平衡位置。但由于耦合了电磁悬浮和液体静压系统，使得其运行情况十分复杂，难以对其进行准确控制，进而影响轴承系统运行的稳定性和可靠性。

近年来，许多学者对机械系统灵敏度分析相关问题进行了深入研究，取得了丰硕的成果。王杏丹等针对未制导系统参数存在摄动问题，基于伴随法推导出与系统动态方程相同规模的伴随方程，并通过一次伴随求解所有可调参数以及摄动参数的动态灵敏度，有效提高了计算效率。BA等针对仿生腿机器人关节上的液压驱动单元，提出了基于位置的阻抗控制方法；提出了1阶灵敏度矩阵法来分析4种工况下4个主要控制参数的动态灵敏度。结果表明：结合相应的优化策略，动态柔度合成理论和灵敏度分析结果可以补偿控制参数，优化不同工况下的控制性能。石晓辉等以手动变速器为研究对象，考虑输入轴转速、齿隙以及转动惯量等因素建立仿真模型，并从冲击能量的角度，采用向前差分法求得各个参数对变速箱齿轮敲击的参数灵敏度规律。KRAVOS等针对最小化参数过程中，最小化参数集难以建立燃料电池的数学模型，提出了一种基于电化学燃料电池模型、参数敏感性分析和D-最优设计方案应用的创新方法。结果表明：应用D-最优设计能增强校准参数信息，使较小数据集的相对标准误差降低一个数量级。此外，信息的增加和可识别性的提高，提高了燃料电池电化学模型的鲁棒性。KUMAR和DAS针对感应电机驱动器在包括低速与零速区域在内的宽速范围内难以控制的问题，提出了一种基于特征值灵敏度的广义分析方法，用于识别在无速度传感器的感应电机驱动系统中速度的主要影响参数。该方法不仅降低了驱动器的复杂性，还提高了整个系统的可靠性。通过仿真与实验的方式证明了该方案的正确性。

综上，目前学者对于参数灵敏度的研究在机械系统各方面均有涉及，但尚未查到有关于磁液双悬浮轴承系统参数灵敏度的研究。因此，本文作者建立磁液双悬浮轴承径向单自由度承载力数学模型，以分析磁液双悬浮轴承系统一阶灵敏度。采用一阶轨迹灵敏度方法和2种灵敏度评价指标，提取影响轴承系统的主要参数。

1 单自由度磁液双悬浮轴承系统非线性方程

根据文献[11-13]，在比例调速阀的调控电压=0、电磁线圈的调控电流=0的情况下，单自由度轴承支承系统的动力学方程为

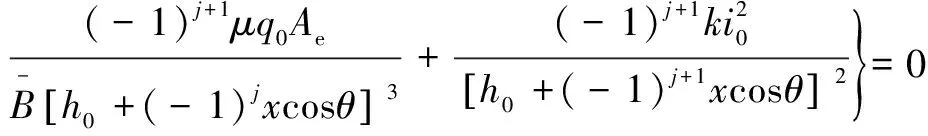
(1)

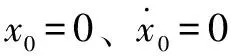
(2)

2 轴承系统一阶轨迹灵敏度分析

由于式(2)包含非线性因素，需要采用轨迹/矩阵灵敏度法进行分析。

2.1 轴承系统状态空间描述

轴承系统状态空间通用表达式为

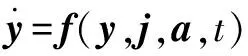
(3)

式中：为维状态变量；为维参数矢量；为与无关的维输入矢量；为时间。

将状态变量、输入矢量和轴承系统内参数作为研究对象，得到状态方程中各矢量表达式为

(4)

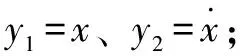
因此，式(3)可展开为

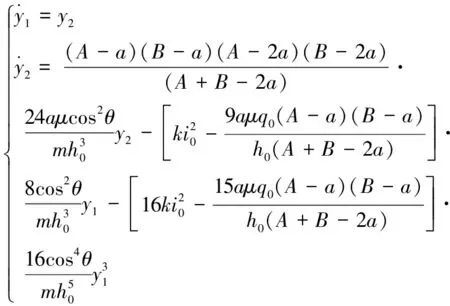
(5)

2.2 轴承系统一阶轨迹灵敏度方程

式(3)可表示为

()=(,)

(6)

式中:=1,2。

状态变量对参数一阶轨迹灵敏度的数学表达式为

(7)

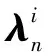
将式(3)对矢量分别求偏导，得到：

(8)

将式(8)展开并将式(7)代入可得：

(9)

2.3 系数项矩阵与自由项矩阵

函数(,,,)对变量进行求偏导，得到系数项矩阵：

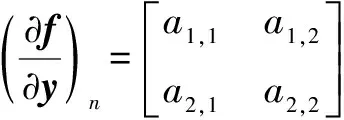
(10)

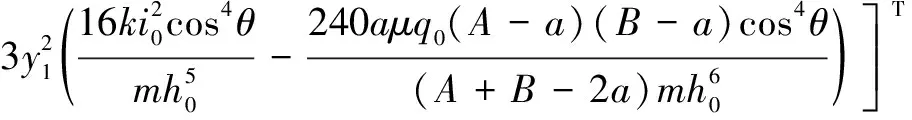
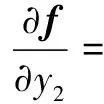
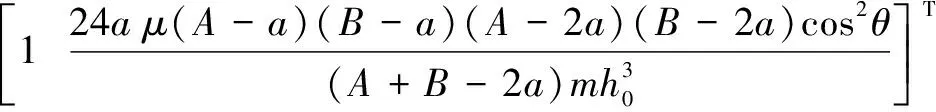
将函数(,,,)对参数矢量求偏导，得到自由项矩阵：

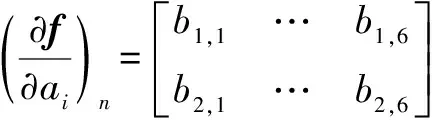
(11)

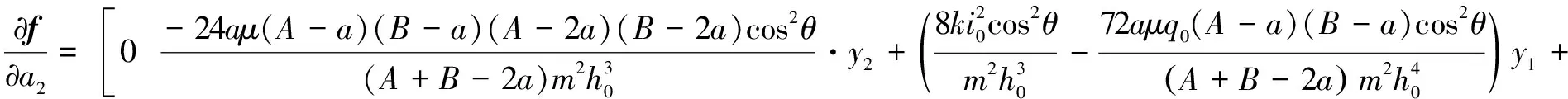
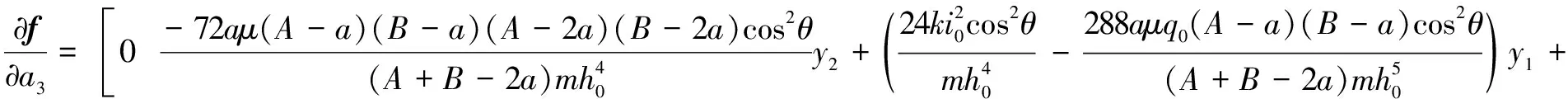
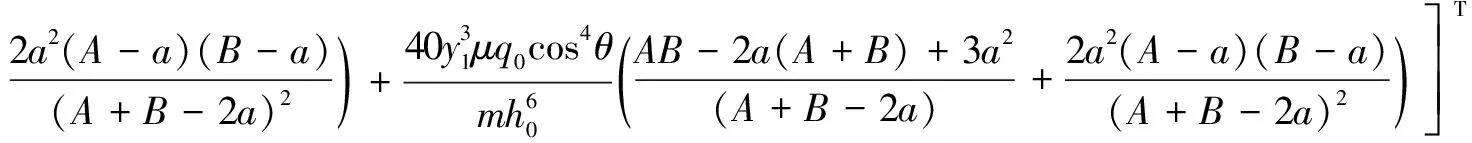
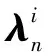
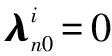
(12)

2.4 轴承系统一阶轨迹灵敏度仿真基础

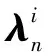
图6 转子位移一阶轨迹灵敏度函数曲线

2.5 轴承系统一阶轨迹灵敏度衡量指标

状态变量Δ同参数矢量Δ之间关系为

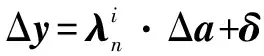
(13)

式(13)中：表示高阶项。根据式(13)可知，假设系统不考虑高阶项参数对当前状态变量变化量Δ的影响，可得出参数矢量变化量Δ同状态变量变化量Δ呈正比例函数关系。

灵敏度评价指标1：规定状态变量的变化量为Δ时，同状态变量的最大值比值乘以百分之百并取其最大值，其中该百分比的表达式如下：

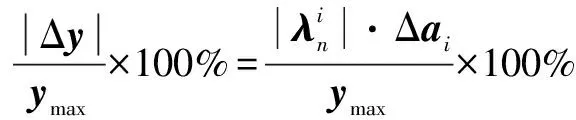
(14)

另外，该百分比大小随时间的改变而变化，得到最大值方程如下：

(15)

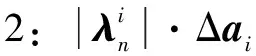
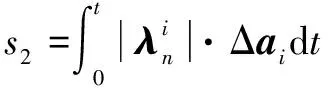
(16)

根据式(14)(15)，得到各不同参数变化1%、2%以及3%时2种灵敏度衡量指标的柱状图，如图7所示。

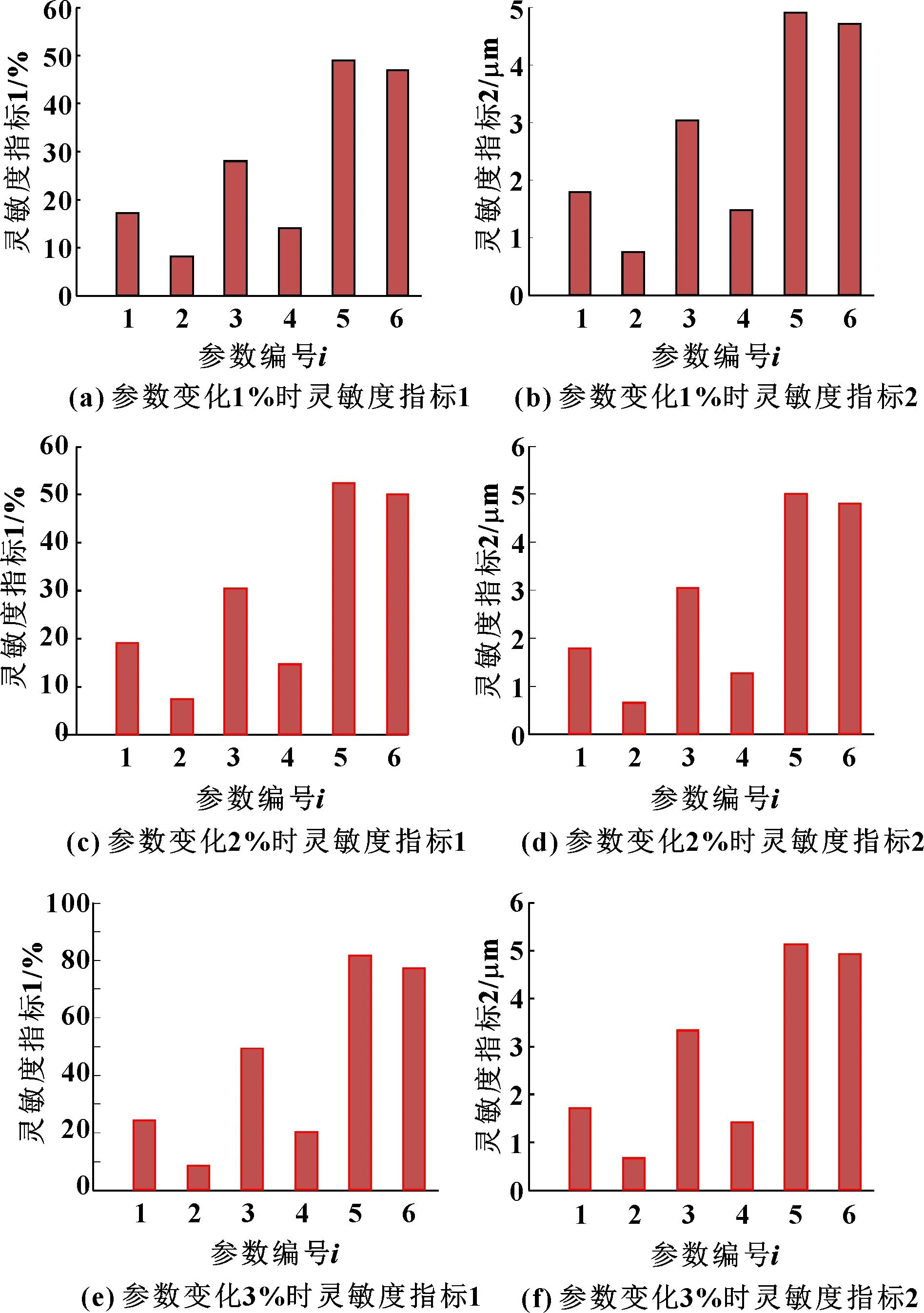
图7 不同Δa下的2种灵敏度衡量指标柱状图

由图7可以看出：随着各个参数发生不断变化，2种灵敏度指标也出现线性变化。其中，各参数变化对轴承转子位移的影响如下：

轴承质量、油液黏度系数、轴承定子封油边宽度的2种灵敏度指标相对于其他参数所占比例均较小，其中轴承质量对轴承转子位移的影响最小；静压力主要参数流量和液膜厚度参数、电磁力主要参数电流的2种灵敏度指标明显大于其他参数，其中流量和电流最大，这是由于它们本身直接影响整个系统力平衡方程，对整个轴承系统影响最大。因此，对整个磁液双悬浮轴承系统稳定性分析中，需重点考虑这些参数对系统特性的影响。

3 结论

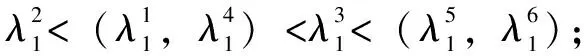
(2)流量、液膜厚度、电流的灵敏度指标明显大于其他参数，其中流量、电流分别为第一、第二影响参数。