滑动轴承半径间隙对转子系统振动特性影响研究

陈坤旭，王东强，董学武，姜海芹

(中原工学院机电学院，河南郑州 451191)

0 前言

随着旋转机械转速和可靠性要求的提高，滑动轴承凭借其承载能力强、工作稳定可靠、寿命长等优点得以广泛应用。轴承作为支承直接作用于转子系统，其动力特性关系到轴承-转子系统的临界转速、不平衡响应、稳定性等。半径间隙和外载荷分别为轴承重要的结构参数和工况参数，直接影响轴承的静动态特性。因此，研究半径间隙和外载荷对滑动轴承性能的影响，对于提高轴承-转子系统稳定性具有重要意义。

大量学者对滑动轴承油膜特性以及轴承-转子耦合系统动力学特性开展了广泛研究。滑动轴承油膜特性的研究大多建立在Reynolds方程的基础上，求解油膜压力分布，获得油膜静动特性系数。文献[4-5]基于有限差分法求解Reynolds方程，并进一步利用改进方法求解油膜压力分布，取得了较好的计算精度，得出有限宽滑动轴承的动特性系数随偏心率的增大而增大的结论，但是未考虑轴承半径间隙和载荷的变化对轴承油膜特性的影响。孙丹等人研究了轴颈涡动轨迹下的油膜力变化规律，通过分析不同涡动频率和轴颈偏心率下油膜力对轴颈做功情况，得出偏心率越大、越有利于转子的稳定。王欣彦等用有限体积法分析了轴承椭圆度、偏心率分别对转子稳定性、油膜压力的影响，但是在工程实际中轴颈的平衡位置、偏心率和偏位角是时变的，则在设计之初可以预先设计转子载荷。张艾萍等运用CFD计算N-S方程来研究滑动轴承的油膜特性，并得出轴承半径间隙对旋转机械转子稳定性起着非常重要的作用，但并未建立完整的轴承-转子系统动力学模型进行验证。魏维等人分析并对比了不同半径间隙和宽度下滑动轴承最小油膜厚度、支撑刚度和阻尼的变化趋势，得出增大轴承半径间隙会降低转子失稳转速，但并未进一步研究轴承间隙对转子系统不平衡响应的影响。甄天辉和唐委校分析了轴承各刚度和阻尼分量随结合面间隙变化的函数关系，得出通过调整间隙可以抑制汽轮机振动的结论。

针对半径间隙和载荷对油膜特性及转子支撑系统动力学特性相关影响研究不够全面的现状，本文作者从流体动力学基本方程出发，使用有限差分法和超松弛迭代法求解Reynolds方程，得到油膜压力分布、各静动特性系数、最大油膜压力和最小油膜厚度的变化曲线。在此基础上，建立考虑滑动轴承半径间隙的轴承-转子耦合系统动力学模型，通过轴心轨迹、时域响应和频域响应，分析半径间隙对由不平衡量引起的转子振动的抑制机制。

1 滑动轴承动力学模型及求解

1.1 滑动轴承动力学模型

建立圆轴承动力学模型如图1所示，有一个外部载荷作用于轴颈，使轴颈中心相对于轴承中心产生偏心距，以及相应的偏位角；滑动轴承半径间隙=-，为轴颈半径；为从竖直方向顺时针算起的角度。延长轴颈中心和轴承中心的连线与轴颈表面两点相交，交线处出现最大油膜厚度和最小油膜厚度。

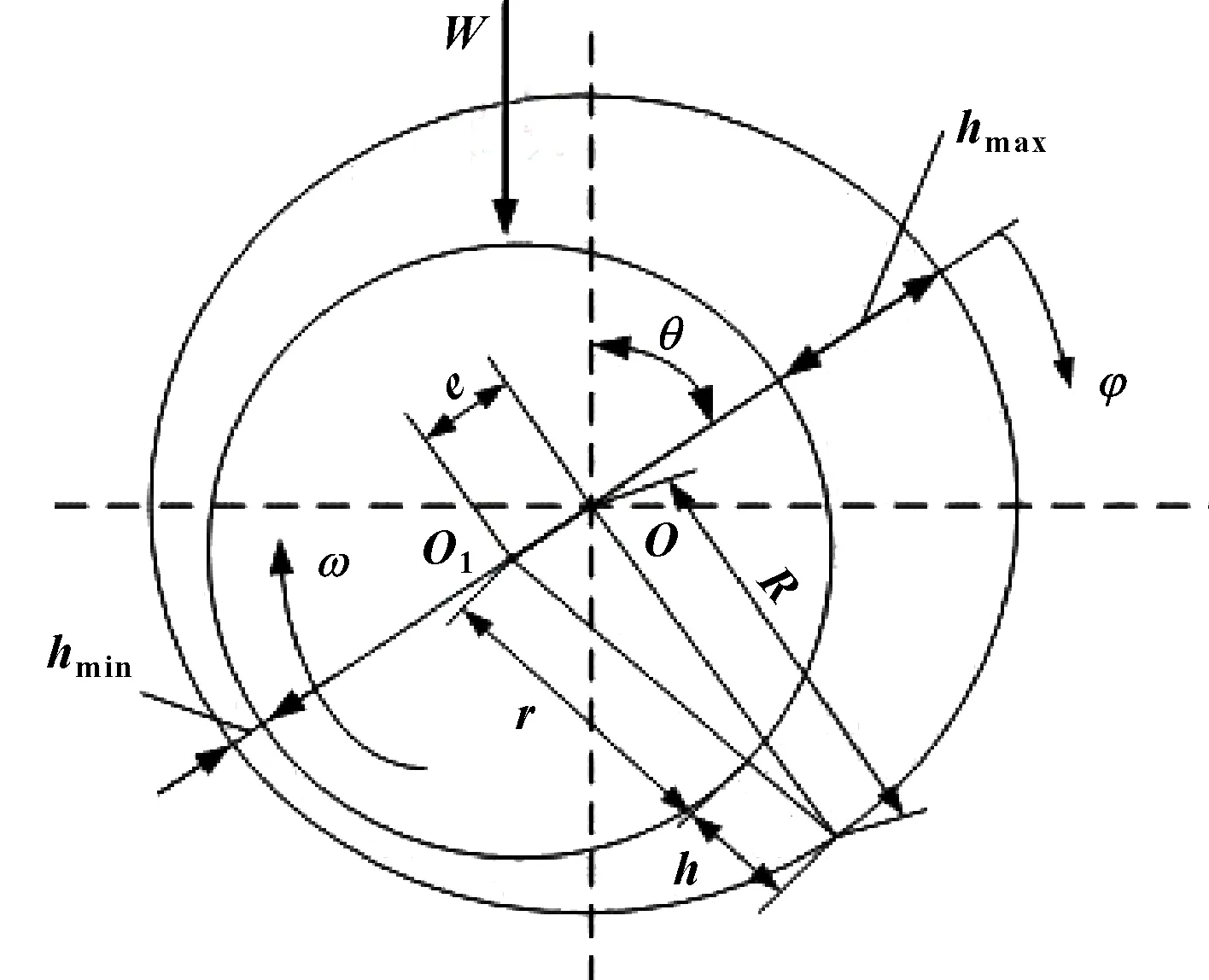
图1 滑动轴承动力学模型

根据图1中的几何关系，由余弦定理得：

=+(+)-2(+)cos

(1)

=-

(2)

两端各加cos，经整理得：

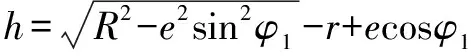
(3)

油膜厚度函数求导后，由于≫sin，油膜厚度函数简化为

=+cos

(4)

偏心率：

=

(5)

在一定假设条件下：润滑油符合牛顿黏性定律，各向同性，不可压缩且为层流流动；润滑油与轴颈、轴瓦表面之间无滑动；油膜厚度较其长度较小；不计润滑油惯性，对油膜中微元体进行受力分析的Reynolds基本方程为

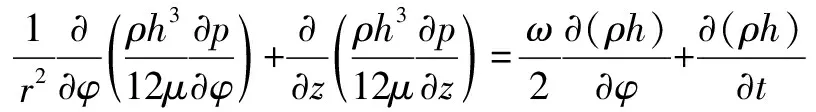
(6)

式中：为油膜压力(N/m)；为轴颈角速度(rad/s)；为润滑油密度(kg/m)；为润滑油黏度(N·s/m)；为轴向坐标(m)；为时间(s)。

为推导和计算方便，将Reynolds方程量纲一化，得到方程：

(7)

使用有限差分法(FDM)求解在每一个离散时间步长滑动轴承的流体压力分布。将滑动轴承的油膜在宽度方向和周向分布上划分和个网格，用周围节点上的压力构造差商，通过超松弛迭代得出离散的油膜压力。采用与滑动轴承油膜的实际工况比较接近的Reynolds边界条件，可以得到比较精确的结果。

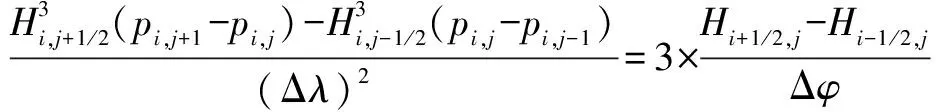
(8)

将式(8)整理成：

,+1,+,-1,+,,+1+,,-1-,,=,

(9)

应用超松弛迭代法求解式(9)，得到油膜力的表达式：

(10)

通过周围4个点上的压力计算(,)节点上的压力。

迭代过程根据相对收敛规则：

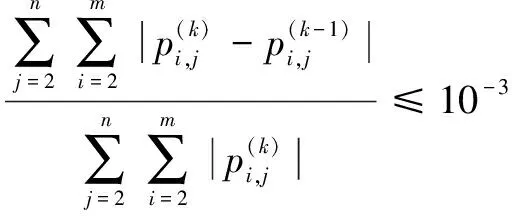
(11)

即允许相对误差取值10。

对滑动轴承的静动特性进行分析，获得轴承油膜压力分布是首要条件。根据压力扰动法，即当轴颈在静平衡位置上作微小振动时，油膜力可以近似表达为轴颈微小位移和速度的线性函数。设油膜力静态位置时、方向的力分量分别为0、0，在油膜区间进行积分，得到轴承水平方向和垂直方向的油膜力公式：

(12)

将油膜力分量对各方向扰动参数求导可得油膜刚度和阻尼：

(13)

偏位角为

=arctan(00)

(14)

联立式(1)—(14)并求解，可以得到滑动轴承静动特性系数。

1.2 运用超松弛迭代法求解流程

运用超松弛迭代法求解的流程如图2所示。

图2 计算流程

1.3 半径间隙和外载荷对滑动轴承静动态特性影响

轴颈在未受到外界干扰时，处于平衡状态，轴颈中心相对轴承中心有确定位置，或者以一定的偏心距恒速绕轴承中心做圆轨迹进动。当轴颈受到外界干扰时，轴颈中心相对于平衡状态产生初位移和初速度，严重时会引起油膜失稳甚至油膜振荡，导致机器部件损坏。轴承支撑刚度和阻尼反映了转子系统抵抗变载荷的能力以及系统的稳定性，因此对滑动轴承动力特性系数的求解是分析轴承-转子系统稳定性的基础。

轴承各静动态特性系数随着载荷、轴颈转速的变化而变化。对比半径间隙在0.6～1.2内对轴承的静动特性系数的影响，得出线性增加外载荷下轴承间隙和滑动轴承各静动特性系数的函数关系。滑动轴承参数如表1所示。

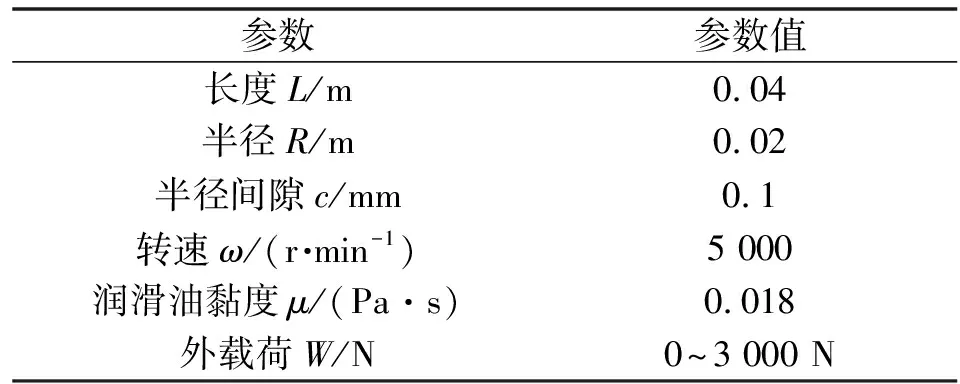
表1 滑动轴承参数

由图3(a)可知：随着外加载荷的增大，偏心率呈非线性增加，最后趋于平稳，随着轴承间隙的增加，偏心率增加速度增加；当轴承半径间隙从0.6增加到1.2时，偏心率曲线变化更加迅速。由图3(b)可知：随着外载荷的增加，偏位角呈非线性下降，最后趋于一个定值。

图3 静特性系数变化曲线

由图3(c)可知：通过调整半径间隙可以改变运行时最小油膜厚度；当载荷较小时，半径间隙大则油膜厚度大，最小油膜厚度随着载荷的增加而减小；小间隙对应的最小油膜厚度曲线下降速率小于大间隙对应的斜率；外载荷约到达100 N后，较小的半径间隙下有较大油膜厚度，最后下降趋势趋于平缓；最小油膜厚度稳定值从0.6～1.2减少53.3%。最小油膜厚度迅速减小,过小时会造成轴承的碰摩，加速轴承的磨损，因此应维持一定的最小油膜厚度，使转子系统不因碰摩而失去生存能力。从图3(d)可见，随着载荷的增加，最大油膜压力大体上呈线性增加，半径间隙较小时，最大油膜压力上升速率较慢。

不同径向间隙下，滑动轴承支撑刚度和阻尼随外载荷的变化曲线如图4所示。以刚度分量、和阻尼分量、为例进行分析。由图4可知：刚度分量整体呈下降趋势且非线性变化，最终随着外载荷的增加趋于一个稳定值，前期下降部分表现为大间隙下降速率更快；刚度分量随着外载荷的增加总体呈线性上升趋势，且表现为大间隙对应的斜率大。

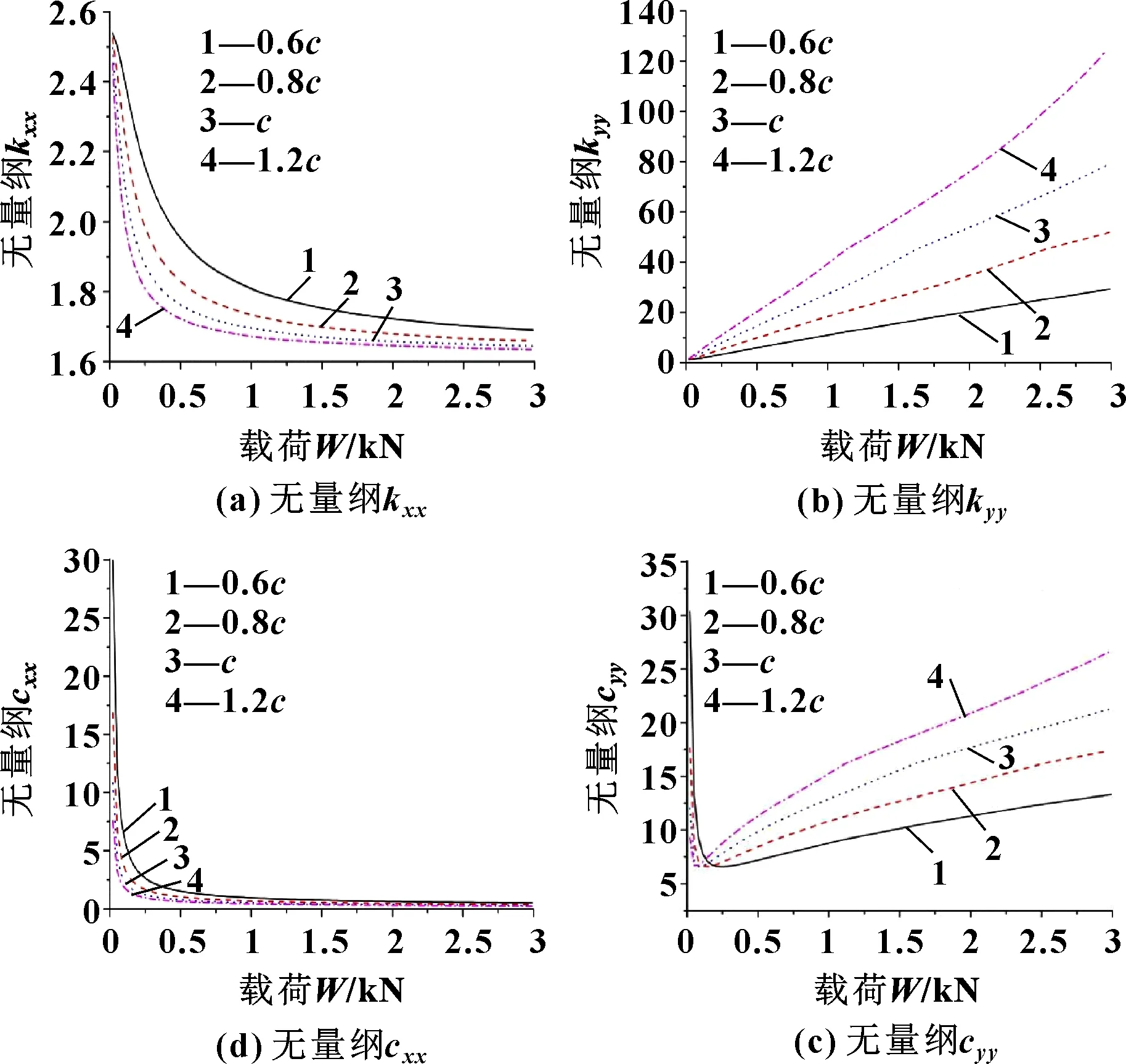
图4 动特性系数变化曲线

由图4还可知：阻尼分量、在不同的间隙下初始值相差都很大，后随载荷增加而下降，且阻尼分量在载荷为0～500 N时变化最迅速，在500 N后曲线下降速度突然降低；阻尼分量随载荷的增加迅速下降之后出现一个拐点，之后呈上升趋势，并随着半径间隙的增大上升曲线的斜率变大。以上对不同半径间隙轴承的动特性函数关系的求解，为轴承-转子耦合系统动力学的研究提供了参考。

2 滑动轴承-转子系统动力学模型及求解

2.1 轴承-转子系统动力学模型

引起转子振动的最常见与最主要的原因是转子不平衡，针对转子系统不平衡引起的振动问题，对不同半径间隙下的转子系统进行动力学分析。建立两端由滑动轴承支撑的单盘转子系统动力学模型，其中轴承载荷采用转子自重。如图5所示，圆盘位于转子中心位置且质心同转子轴线存在偏心距0.1 mm，轴承转子系统参数如表2所示。

图5 轴承-转子动力学模型

表2 轴承-转子系统参数

考虑陀螺力矩和不平衡力的轴承-转子系统振动微分方程式为

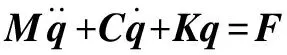
(15)

式中:为质量矩阵；为阻尼矩阵；为刚度矩阵；为位移向量；为系统激励。阻尼矩阵考虑转子陀螺效应。系统激励包括转子不平衡激振力、轴承非线性油膜力和重力外激励向量。

2.2 不同半径间隙下轴承-转子系统振动响应

根据图5建立滑动轴承转子耦合系统模型有限元模型，将计算得出的不同半径间隙轴承动力学特性参数代入动力学方程，利用四阶Runge-Kutta法对滑动轴承支撑的转子系统振动微分方程进行时间步进求解，得到轴承-转子系统在不同半径间隙下的动力学响应。

轴心轨迹可以反映轴承和转子系统的工作状态，是判定轴承-转子系统稳定性和轴承设计参数是否合理的一个重要参考依据。图6所示的转子系统轴心轨迹由于不平衡力矩和油膜涡动呈椭圆内八形，随半径间隙的增加油膜涡动现象越来越明显，转子振动响应增大，且椭圆平均直径越来越大，逼近轴承间隙圆直径，导致轴颈与轴承容易发生碰摩而使转子失去生存能力。

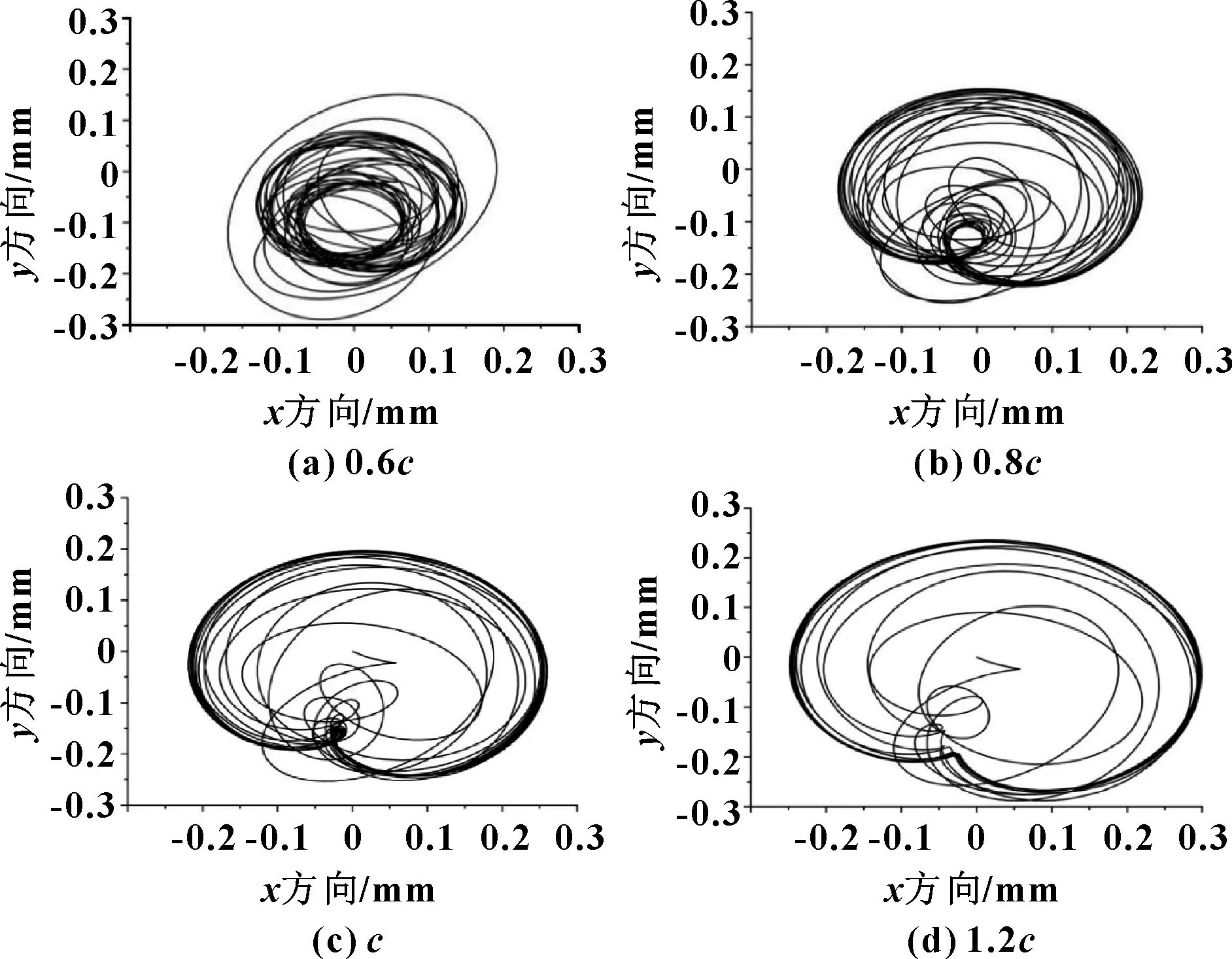
图6 轴心轨迹

图7所示为不同间隙下时域和频域响应，以不平衡质量节点处的振动幅值为衡量标准。由图7(a)(b)可知：半径间隙为1.2时，最大振幅在方向约为0.25 mm、方向约为0.27 mm；半径间隙为0.6时，最大振幅在方向约为0.115 mm、方向约为0.12 mm。转子振幅随着半径间隙的减小明显减小，可见通过调整轴承半径间隙可有效抑制转子振动，使轴承转子系统更安全地运行。

由图7(c)(d)可知：幅频特性曲线由多个频率成分组成，其中以1阶次谐波幅值最为突出，反映出转子不平衡是影响转子系统稳定性的主要因素，此外还存在由于油膜非线性引起的响应。文中主要分析半径间隙对1阶次谐波幅值的影响。由图7(c)(d)可见:和方向最大振动位移在转子系统第1阶固有频率42 Hz附近，随着半径间隙的减小，轴承动力特性发生改变，由于转子不平衡引起的最大振动响应幅值显著降低。

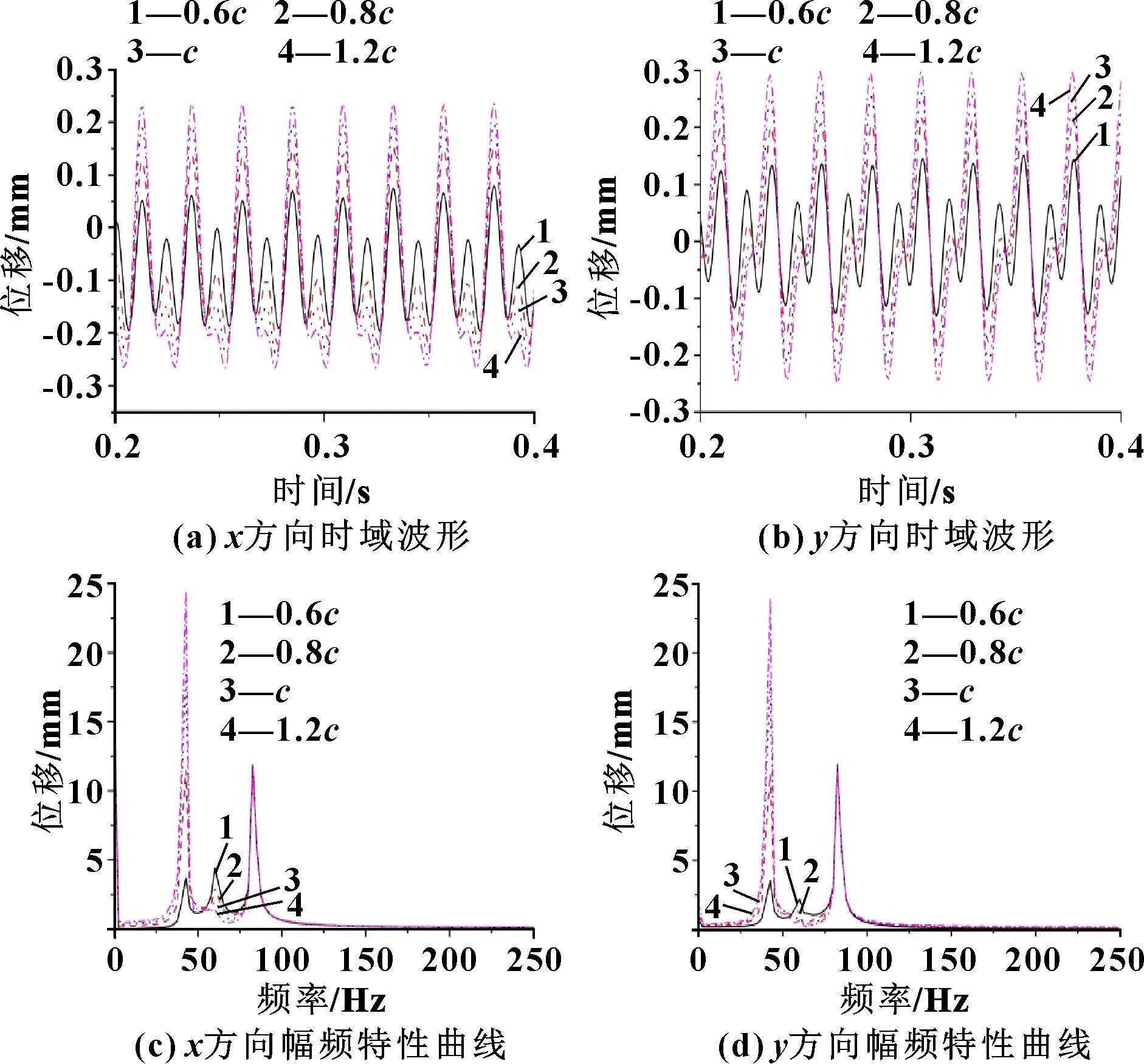
图7 轴承支撑转子的瞬态动力学响应

3 结论

(1)在一定转速下，载荷对滑动轴承动力学特性的影响不可忽视，随着载荷的增加，轴承阻尼和刚度剧烈变化。载荷过大时，最小油膜厚度随着载荷的增加而迅速减小，导致轴颈下降到轴瓦底部无法形成动压油膜。

(2)滑动轴承半径间隙大小同样对轴承的动力学系数有显著影响。在一定转速下，随着半径间隙在一定范围内减小，轴承承载能力变大，因此存在最佳半径间隙使得油膜在能够提供稳定的支撑和阻尼的同时，能保证转静子不发生碰摩现象。

(3)通过调整轴承半径间隙，可以有效减小因转子系统不平衡而产生的振动幅值，降低转子系统的不平衡敏感度，为工程中通过调节轴承半径间隙来抑制转子系统振动提供参考。