基于LFM的协同过滤算法研究及实现
李盼颖 韩雨轩 温秀梅,3,* 张书玮
(1.河北建筑工程学院,河北 张家口 075000;2.哈尔滨工业大学(深圳),中国 深圳 518055;3.张家口大数据技术创新中心,河北 张家口 075000)
1 引 言
协同过滤算法是指利用用户历史信息为用户建立模型进而做出推荐的一类算法.本文介绍的隐语义模型LFM(Latent Factor Model,LFM)的思想是训练一个模型,然后挖掘出物品存在的隐藏特征,这些特征能够解释用户给出这样分数的隐藏原因,以隐藏特征为纽带,进一步挖掘出矩阵中某些未评分物品与隐藏特征之间的关联,从而进行预测.
推荐系统非常依赖用户对物品产生的行为数据,但纵观整个推荐系统,用户不可能对每个物品都产生过行为,则获取到可用的行为数据往往非常稀疏,数据的稀疏性会影响最终的推荐准确度.因此,通过隐语义模型LFM进行建模,对历史数据进行矩阵分解,最后利用降维后分解矩阵进行一系列操作.
2 隐语义模型
2.1 LFM模型介绍

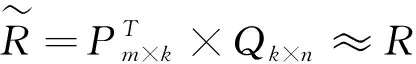
(1)
图1是LFM建模的过程,通过建模,可以得到降维矩阵P和Q.其中P和Q矩阵中引入了3个隐藏特征,这3个隐藏特征把用户特征矩阵和物品特征矩阵联系起来.
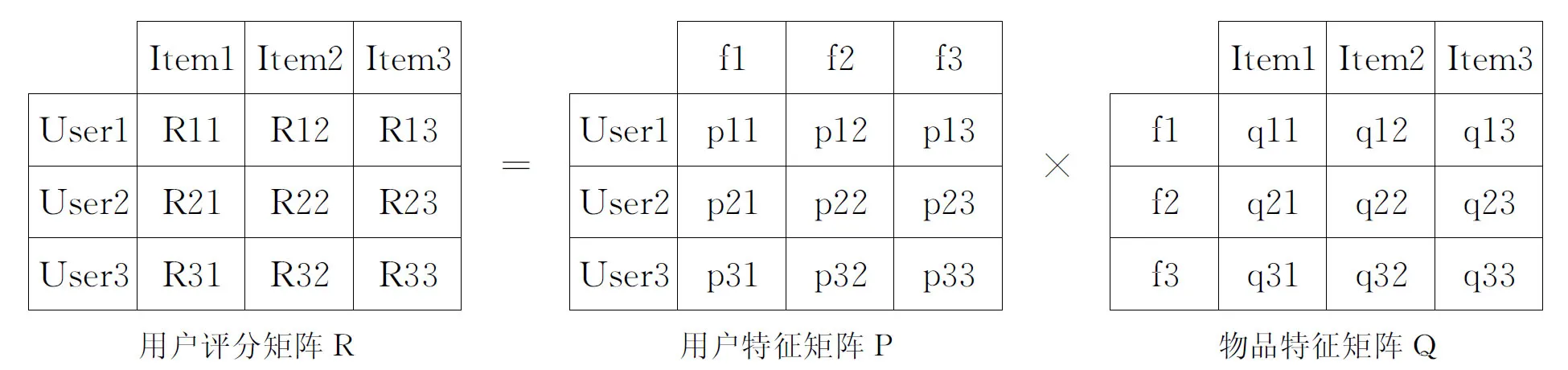
图1 LFM 建模过程
2.2 LFM模型的优点
从上图的LFM模型可以看出,该模型有以下几个优点:
(1)分类粒度可设置[1].在图1中,通过建模引入了f1,f2和f3三个维度,维度的数量是通过设置LFM模型的分类数来控制的分类粒度.
(2)无需手动设置类别[2].矩阵P和Q中的类别数量是可设置的.类中最具有代表性的项目item是基于用户行为数据集R自动聚类产生的,因此,不需要用户手动分类项目.
(3)可以得到每个用户User对所有类的兴趣度,即使该用户没有实际产生某类的行为数据,也可以通过模型计算出用户对该类的隐含兴趣度[3].
2.3 损失函数

C=∑(u,i)∈R0(Ru,i-R^u,i)2+Reg=∑(u,i)∈R0(Ru,i-PuT×Qi)2+λ∑u||Pu||2+λ∑i||Qi||2
(2)
式(2)中的λ∑u||Pu||2+λ∑i||Qi||2是为了防止过拟合,而加入正则化项,其中正则化项系数λ可以通过交叉验证获取最优值.对于最小化过程的求解,一般采用交替最小二乘法(Alternating Least Squares,ALS)或随机梯度下降算法来实现.
2.3.1 最小二乘法ALS
ALS算法的核心想法是:对于求解P和Q两个未知矩阵问题,和之前的对于含两个未知数X和Y求导问题比较类似.思路都是一样,固定其中一个值,把另外一个当成变量,通过损失函数最小化来进行求解,反之亦然.反复执行相同操作,直到满足一定的阈值条件,或者达到迭代上限.这就是一个经典的最小二乘问题.最小二乘法的具体过程如下:
a.固定当前Q0的值,求解P0
b.固定当前P0值,求解Q1
c.固定当前Q1,求解P1
d.重复上述操作,直到损失函数C收敛,迭代结束
根据上述算法过程,利用ALS算法来进行操作:
(1)以固定P,求解Q为例
(2)由于每一个用户U都是互相独立的,当固定P时,物品特征向量Qi取得的值与其他物品特征向量无关,所以每一个Qi都可以单独求解
(3)优化目标minP,QC可转化为公式(3):
minP[∑(u,i)(Ru,i-PuT×Qi)2+λ∑u||Pu||2]=∑uminP[∑i(Ru,i-PuT×Qi)2+λ∑u||Pu||2]
(3)
Lu(Pu)=∑i(Ru,i-PuT×Qi)2+λ||Pu||2
(4)
(4)最终目标变成了:求每一个物品特征向量Qi,使得公式(4)取得最小值
(5)公式求导后,Qi结果如下:
Qi=(PPT+λI)-1PRi
(5)
反之,求解Pu也是同样步骤:
Pu=(QQT+λI)-1QRU
(6)

2.3.2 随机梯度下降算法
对于损失函数Lu(Pu)求最小数,还可以采用随机梯度下降算法,进行迭代.损失函数L(P,Q):
L(P,Q)=∑(u,i)∈R0(Ru,i-PuT×Qi)2+λ∑u||Pu||2+λ∑i||Qi||2
(7)
对每一个Pu求偏导后,接着进行梯度下降迭代:

(8)
同理,有:
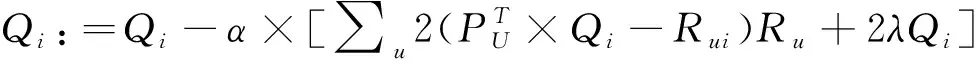
(9)
其中,α是学习速率,α越大,迭代下降的速度就会越快.
3 LFM模型实验
3.1 数据集分析
对于LFM模型的实验验证,本文采用Movie Lens数据集中的ratings来验证损失函数最优化算法,数据集中存储了10万多条用户对电影的评分数据,其中数据评分值为1到5,数据集情况如表1所示.

表1 数据集简介
3.2 实验结果与分析
该实验最终采用的是随机梯度下降算法来进行最优损失函数的计算.实验中需要用到迭代思想,迭代次数可随机选择,迭代是为了训练并输出用户特征矩阵P和物品特征矩阵Q,number_LatentFactors是隐藏特征数量,number_epochs是迭代次数,alpha为学习参数,lambda是正则化系数.注意每次迭代后,损失函数的变化趋势大不相同.算法核心代码如下:

对于训练数据集Movie Lens,本文选择的迭代次数number_epochs为100,alpha学习参数为0.02,lambda正则化系数为0.01.为了验证隐藏特征向量对模型训练的结果有怎样的影响,因此,在实验中分别选择隐藏特征特征向量为5和10来进行比较.LFM模型训练结果如图2图3所示:

图2 隐藏特征为10 图3 隐藏特征为5


表2 部分真实值与预测值对比
4 结束语
本文主要利用隐语义模型LFM来构建模型,采用随机梯度下降算法使损失函数取得最优值.而且根据该模型还可以预测出未评分项目的评分,对减少评分矩阵的稀疏性以及冷启动问题有一定的作用.在实验验证的时候,迭代次数number_epochs,alpha学习参数,lambda正则化系数的取值比较单一.为精确验证实验结果,在以后实验验证时可以丰富数据的多样化来提高推荐效率.
在实际情况中,有些用户的个人属性以及评分差异性等问题也会影响用户打分.因此,在接下来的研究中,在构建模型时考虑加入这些影响因素,使得推荐效果更加精确.

