半空间上的Bohr型不等式
2022-09-15 00:28:42陈铭新李程鹏王建飞
华侨大学学报(自然科学版) 2022年5期
陈铭新, 李程鹏, 王建飞
(华侨大学 数学科学学院, 福建 泉州 362021)
1914年,Bohr[1]在研究Dirichlet级数绝对收敛问题时得到定理A.
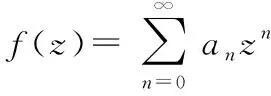
2010年,Fournier等[2]考虑一般单连通域Ω⊃D上的解析函数,并定义了函数族B(Ω)的Bohr半径,记为BΩ∈(0,1),即
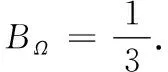
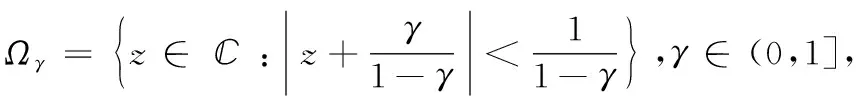
1 几个引理
设f和g是单连通域0∈Ω上的两个解析函数,若存在一个函数φ,其中,φ在Ω内解析,且φ(Ω)⊂Ω,φ(0)=0,则在Ω上,g=f∘φ,称g从属于f,记为gf.
特别地,当f单叶时,g从属于f,等价于g(D)⊂f(D),g(0)=f(0).当gf时,|g′(0)|≤|f′(0)|.
为了给出主要结果,需引入引理1~3.
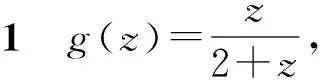
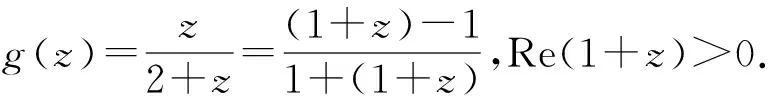
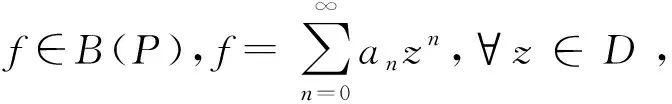
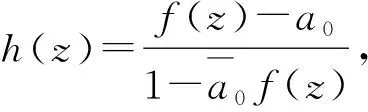
(1)
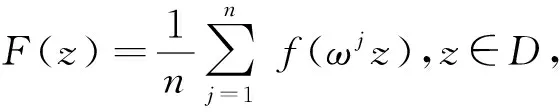
由f(z)的幂级数展开式和F(z)的定义,有
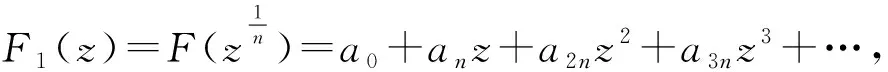
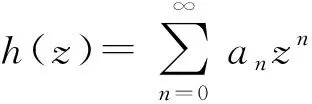
2 主要结果及其证明
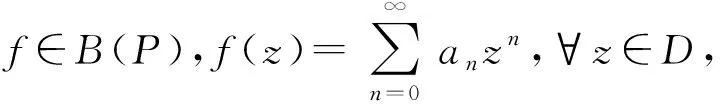
证明:由引理2,有
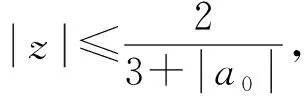
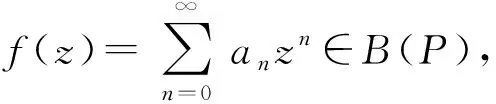
解得|a0|=1,即|f(0)|=1.由解析函数的最大模原理有f(z)=c,|c|=1,证明完毕.
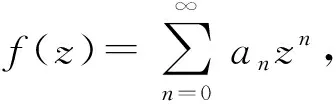
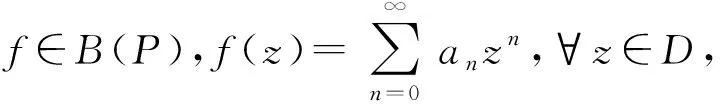
证明:令|a0|=a∈[0,1],由引理2,有

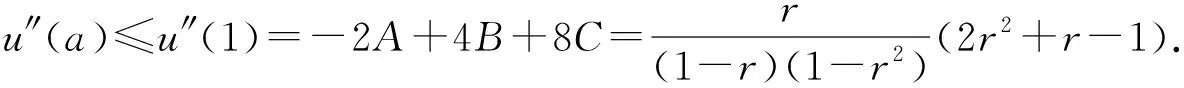
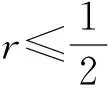
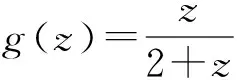
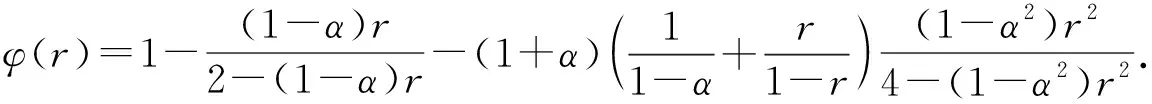
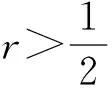
假设f=u+iv是复平面区域Ω⊂上的二次连续可微的复值函数,若f满足Laplace方程则称f为Ω上的调和映射.特别地,若Ω为单连通域,则f可表示为其中,函数h和g均是Ω上的解析函数,并分别称之为f的解析部分和共轭解析部分.此时,其Jacob行列式为Jf(z)=.Lewy[11]证明了调和映射f在Ω上是局部单叶保向的,当且仅当,Jf(z)>0,∀z∈Ω.若|h′|≠0,定义wf=g′/h′为f的第二伸缩商.显而易见,Jf(z)>0等价于|wf(z)|<1.有关多变量的Bohr半径可参考文献[12-15].
考虑P上的调和映射,并得到了一个限制在D上的Bohr型不等式,有定理3.
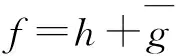
证明:函数h(z)在P内解析,|h(z)|≤1,z∈P.由引理2,可得
又由引理3,有
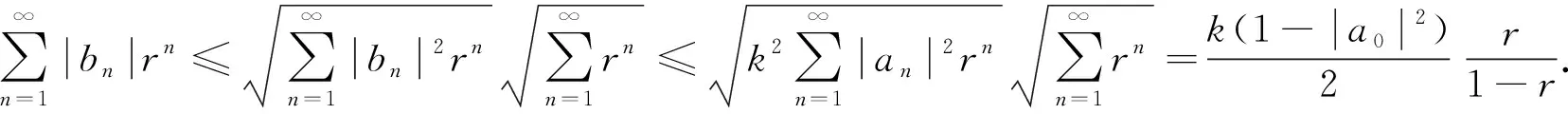
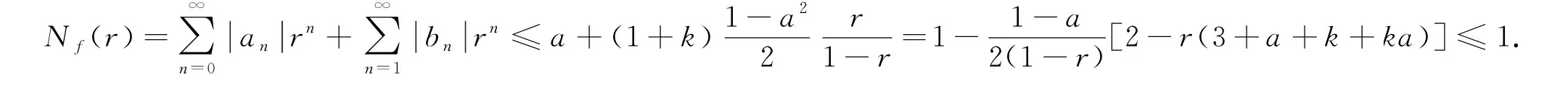
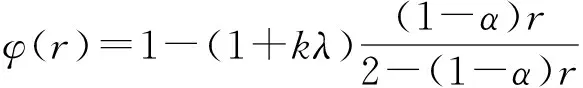
猜你喜欢
数学物理学报(2021年6期)2021-12-21 06:23:56
基层中医药(2021年3期)2021-11-22 08:08:00
福建教育学院学报(2021年1期)2021-03-06 09:22:24
林业科技(2020年3期)2021-01-21 08:28:40
人民调解(2019年2期)2019-03-15 09:30:42
数学年刊A辑(中文版)(2018年1期)2019-01-08 01:58:18
中文信息(2017年12期)2018-01-27 08:22:58
中央民族大学学报(自然科学版)(2015年2期)2015-06-09 08:45:18
郑州大学学报(理学版)(2014年2期)2014-03-01 04:20:50
河南科技(2014年11期)2014-02-27 14:10:11

