结合PCA的t-SNE算法的并行化实现方法

徐旸， 王佳斌， 彭凯

(华侨大学 工学院， 福建 泉州 362021)

大数据可视化是大数据研究领域的核心内容之一[1]，其中，高维数据可视化尤为关键，降维可视化方法[2]是高维数据可视化的一种重要技术，它将高维数据转换为二维或三维的低维数据，并可视化于散点图中[3].数据降维[4]的目标是在低维空间映射数据内部结构，并充分地保留原来高维数据的重要信息.梁京章等[5]提出核主成分分析(KPCA)法，通过核函数的作用，将数据映射至高于现存的维度中，再通过线性降维的手段进行处理. Roweis等[6]提出的局部线性嵌入(LLE)和Tenenbaum等[7]提出的等距离特征映射(ISOMAP)是流行学习中的代表算法，这两种算法在高维空间中观察数据的最潜层特征后，根据两个维度空间的映射关系，将数据的主要特征关系映射于低维空间.Maaten等[8]提出基于t分布的随机近邻嵌入(t-SNE)算法，通过高维空间和低维空间中的条件概率关系，采用长尾t分布实现降维效果.基于此，本文提出一种结合主成分分析(PCA)的t-SNE算法的并行化实现方法.

1 相关工作

1.1 主成分分析法

主成分分析法的目的是在尽可能减小原始信息损失的同时压缩、简化数据，去除冗余的噪声数据.主成分分析法提取数据的主要特征，将原有数据重构为新的相互无关的综合变量集，新变量集的数据量小于等于原数据量.主成分分析法能够有效地展示各变量的映射关系和内部结构.

主成分分析法主要有以下3个计算步骤.

1) 建立初始关系数据矩阵X，有

(1)

2) 标准化初始关系数据矩阵元素为

(2)

(3)

(4)

使用奇异值分解(SVD)法求解相关系数矩阵R的特征值(λ1，λ2，…，λm)和相应的特征向量αj，αj=(αj，1，αj，2，…，αj，m)，j=1，2，…，m.

3) 选择重要的主成分分量.方差贡献率cj为

(5)

式(5)中：λj为第j个主成分分量的特征值.

累积贡献率δj为

δj=c1+c2+…+cj.

(6)

主成分分量的筛选标准为δj≥85%，可得主成分分量为

(7)

式(7)中：x1，x2，…，xm为标准化后的矩阵向量元素.

1.2 t-SNE算法

t-SNE算法是对称随机近邻嵌入(SNE)算法的改进[9-10]，t-SNE算法利用条件概率分布替换传统的距离表示，映射数据点在高维和低维空间之间的距离相似关系，在更好地维持初始数据结构的前提下，展示其内部的聚类特点.t-SNE算法有以下5点计算思想.

1) 在高维空间中，高斯分布pv|u表示点xv，xu互为邻近点的概率.当xv与xu之间的距离越近，pv|u越大；当xv与xu之间的距离越远，pv|u越小.pv|u为

(8)

式(8)中：定义pu|u=0；σu为高斯分布的方差；xk为高维数据.

2) 在对称SNE中，高维空间中的离群点xu与其他数据点xv的距离都很远，则xu的联合概率分布pu，v均较小.pu，v为

(9)

式(9)中：s为数据点的总数.

3) 同理，在低维空间中，用t分布定义数据点之间的关系，则xu的低维表示形式yu的联合概率分布qu，v为

(10)

式(10)中：yv，yk，yl分别为数据点xv，xk，xl的低维表示形式；t分布的自由度设为1.

4) 利用相对熵(KL)距离可得代价函数C，有

(11)

式(11)中：P，Q分别为高维空间和低维空间中所有数据点的联合概率分布.

5) 使用梯度下降法进行优化，有

(12)

t-SNE算法的具体执行步骤如下.

输入：s个D维的向量χ={x1，x2，…，xs}映射到二维或三维空间，定值困惑度为Prep，迭代次数为T，学习率为η，momentum项系数为β(t)

输出：低维数据y={y1，y2…，ys}

步骤：

步骤1点xu的方差σu使用二分查找进行计算；

步骤2通过式(8)，(9)计算成对数据点的pv|u和pu，v；

步骤3初始化低维数据y1，y2，…，ys；

步骤4通过式(10)计算低维数据的qu，v；

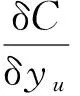
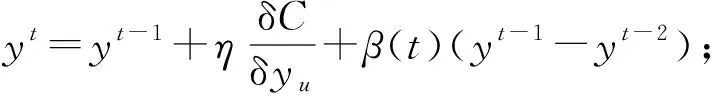
步骤7重复步骤4～6，完成初始设置的迭代次数T.

2 结合PCA的t-SNE算法及其并行化实现

随着数据体量和数据维数的增长，t-SNE算法使用梯度下降法进行反复迭代，计算低维空间中数据点的分布情况，此时，产生的中间结果快速增多，内存压力逐渐变大，当内存不足时，只能将结果存储在磁盘中，这将大幅降低算法的效率.

由于Spark平台[11-13]是开源的通用分布式内存计算框架，通过驱动主节点程序实现任务的分发、调度执行和聚合结果，可解决内存压力过大导致的算法效率低下问题.

2.1 结合PCA法的数据并行化预处理

由于原始数据的维度较高，数据特征值过多，计算数据点之间成对距离的时间复杂度很高，导致算法的整体运行时间增加.而主成分分析法由于轻量化，收敛速度快，能够快速地找到噪声点，在尽可能减少数据损失的情况下压缩和简化数据，节约内存，从而减少可视化结果受噪声点的干扰，去除冗余信息[14].因此，在数据预处理阶段使用Spark平台的Mllib机器学习库[15]中的分布式主成分分析法减少数据维度，既不会严重扭曲数据点之间的距离，又可以去除噪声数据.

首先，数据被分块存储于不同的分区上，对矩阵A(RowMatrix类型)的格拉姆矩阵进行求解，矩阵中行和列的提取由Map回调函数执行，再发送给各执行节点，其结果由Reduce回调函数获得；然后，使用SVD法求解协方差矩阵W[16]，再用特征值、特征向量生成主成分分量；最后，完成的数据再重新分发并保存到分布式文件系统中.

数据预处理流程图，如表1所示.

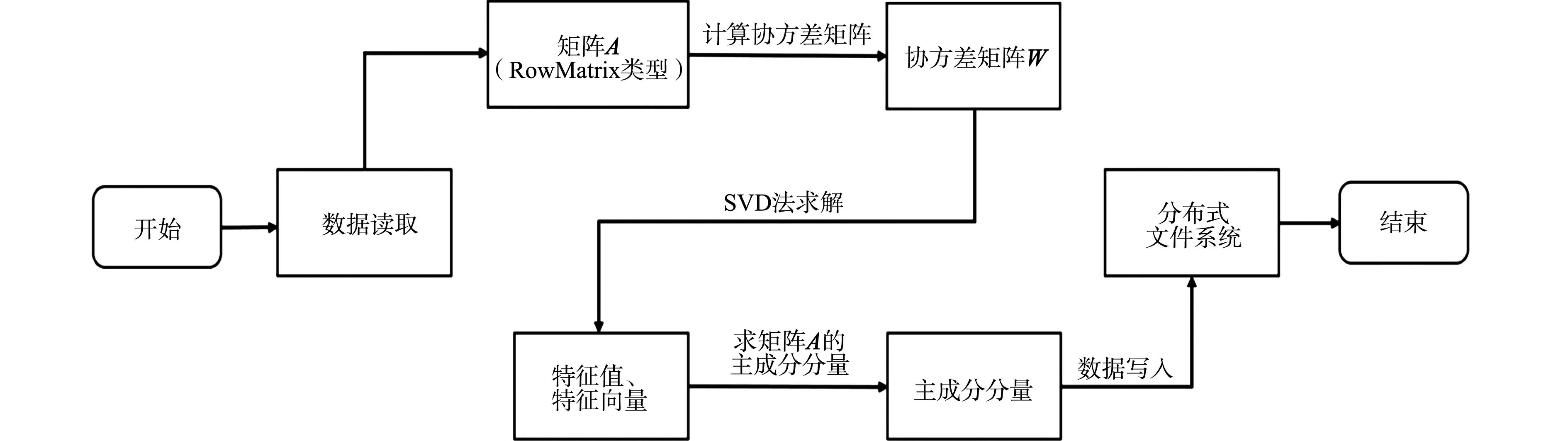
图1 数据预处理流程图Fig.1 Data preprocessing flow chart

2.2 高维空间中点的相似性的K-NN图表示

K最邻近(K-NN)图是基于K-NN算法构造的多节点关系图[17].对于空间中的s个节点，找出与任一节点xs距离最小的K个邻居x1，x2，…，xK，这里的距离度量方式可以自行设定，找到邻居节点后，将其与xs进行连接.空间中其他节点同理，由此可得K-NN图.

，

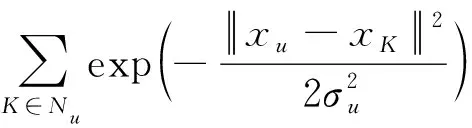
(13)

由此大幅降低了计算量.文中构建K-NN图的算法是制高点(VP)树方法，时间复杂度为O(UNlgN).

2.3 多节点并行执行t-SNE算法

实现Spark平台的连接和访问，任务控制节点Driver Program创建SparkConf和Spark Context对象，再对分布式文件系统(HDFS)上预处理完成的数据创建弹性分布式数据集(RDD)，并分发至每个工作节点，读取分区中的数据集，并有序选择数据点xu，xv作为起始点，生成RDD1，通过Map回调函数计算pu，v，生成RDD2，触发Cache缓存算子，通过Map回调函数计算低维分布qu，v，生成RDD3.进入Combline阶段，优化成本函数，更新qu，v，生成RDD4，判断是否继续迭代.达到预先设定的迭代次数后，RDD4启动ReduceByKey算子，将所有结果汇聚到同一分块，输出最终的低维空间中所有数据点的矩阵Z，完成降维目标.在这些执行步骤中，各工作节点的中间结果保存在内存中，完成后的数据集中到任务控制节点，触发SaveAsTextFile算子，并将最终结果写入HDFS.

并行执行算法流程图，如图2所示.

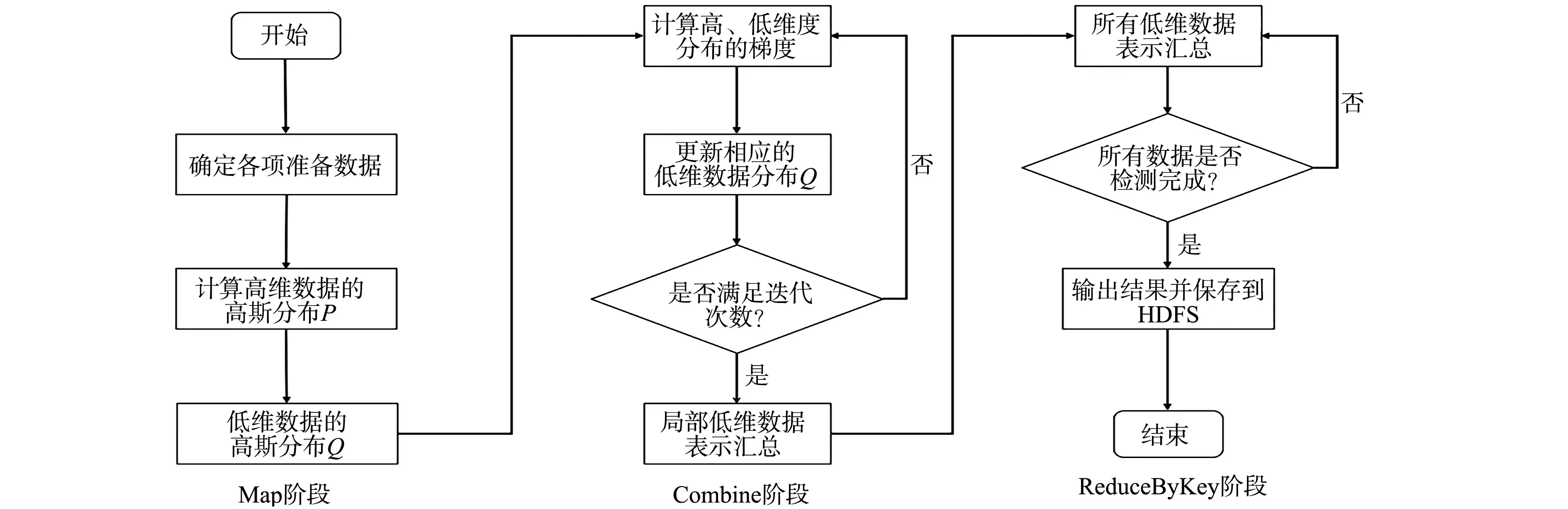
图2 并行执行算法流程图Fig.2 Parallel execution algorithm flow chart

在进行并行计算时[18]，Spark平台将RDD分发到不同的工作节点上，触发缓存机制可以在内存中实现RDD显式持久化，使中间数据重复使用，并将结果缓存到内存中；在计算低维空间中的数据分布时，存储在内存中的数据发挥作用，减少了读取时间，加快迭代过程.因此，对于需要反复迭代计算的算法，内存计算可有效地优化时间成本.在Spark平台中，各任务共同使用广播发送变量，变量在每个计算节点上运行和备份，减少了各数据在传输过程中的消耗，提升了算法的效率.

3 实验结果与分析

为测试文中算法的性能，从运行效率、加速比、扩展比、可视化效果和精确度5个方面进行分析.

3.1 实验环境

基于Vmware虚拟平台，搭建Spark平台集群环境.创建3台虚拟机，其中，1台虚拟机为主要节点，其他两台虚拟机为从节点.每个节点CPU信息为Intel○RCoreTMi7-9750，运行内存为2 GB，硬盘读写速度为1 TB·s-1，集群操作系统为Centos7，Hadoop软件版本为2.8.3，Spark平台的版本为2.3.0.t-SNE算法的单机实验环境如下：CPU信息为Intel○RCoreTMi7-9750，运行内存为16 GB，硬盘数据读写速度为1 TB·s-1.

实验采用的数据集为BREAST CANCER，MNIST和CIFAR-10[19-20].根据数量级，将MNIST数据集分为训练集和测试集，其中，测试样本10 000个，训练样本60 000个，每个样本均为1个784维度的高维数据.

3.2 运行效率

将MNIST数据集分别运行于单机环境和Spark平台，通过处理时间(tc)衡量文中算法的运行效率.不同数量级的数据集在单机环境和Spark平台的运行效率对比，如图3所示.图3中：w为节点数.

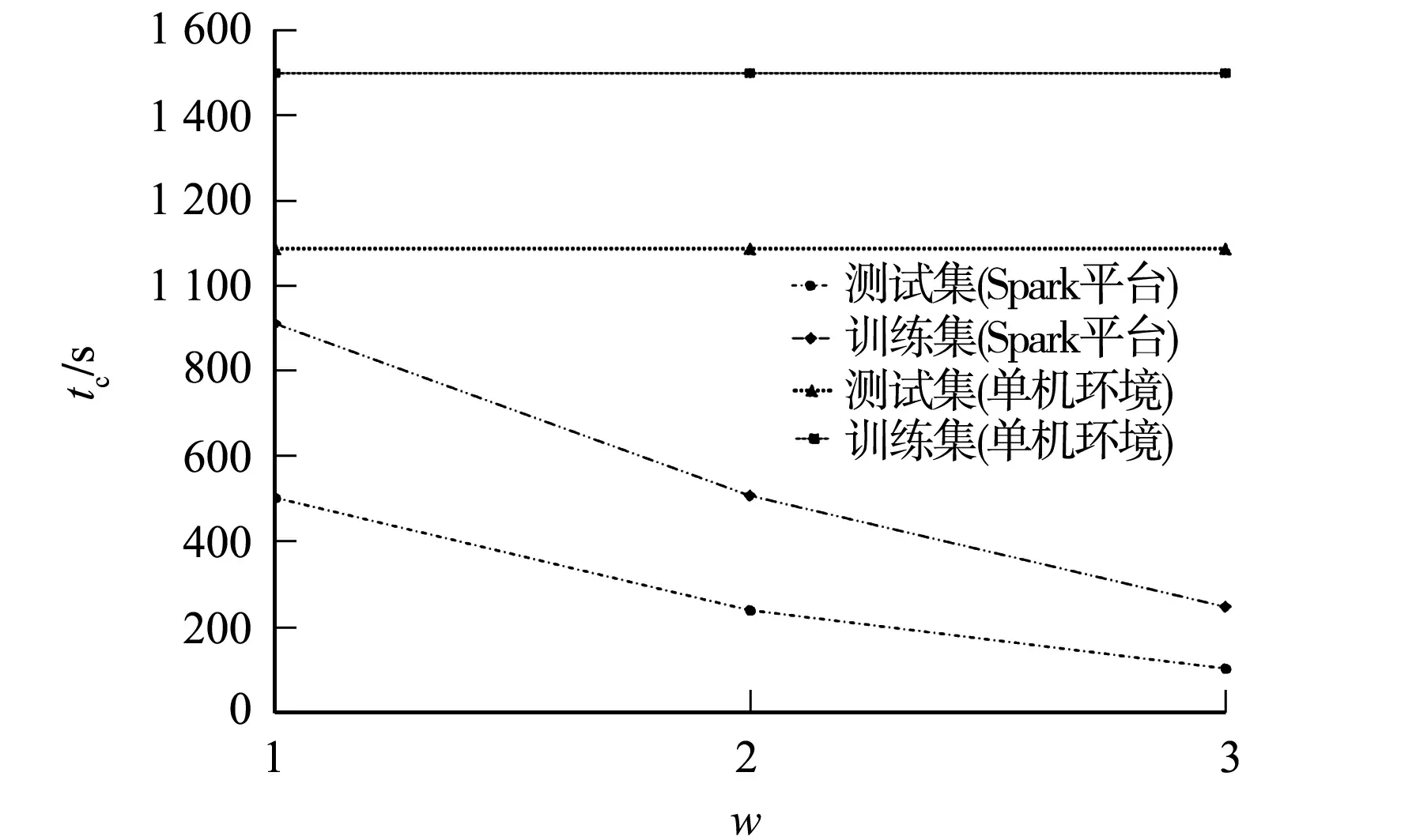
图3 单机环境和Spark平台的运行效率对比Fig.3 Comparison of operational efficiency between stand-alone environment and spark platform

由图3可知：当使用同一数据集在集群中进行实验时，在Spark平台中单个节点的运行效率远高于单机下的运行效率；数据的处理时间随着集群中的节点数的增加而减少，表明算法的执行速度随着节点数的增加而提高，同时，大规模数据集的处理速度随集群中节点数的增加而提高.

3.3 加速比和扩展比

加速比(S)和扩展比(E)是衡量算法并行化的指标.并行化性能的优劣由单个节点运行的时间与多个节点并行的时间的比值进行量化，并行化性能与加速比成正比.加速比的计算公式为

(14)

式(14)中：t1为算法单个节点运行的时间；tw为算法多个节点并行的时间.

扩展比是加速比和节点数的比值，其计算公式为

E=S/w.

(15)

文中算法在MNIST数据集的加速比和扩展比，如图4，5所示.由图4，5可知：在Spark平台中，随着参与计算节点的增多，加速比随之逐渐增大，扩展比随之逐渐减小；随着数据集的增大，加速比的增长随之变快，而扩展比随之趋于平稳，算法的并行化的优势也愈发明显.

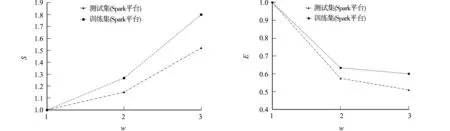
图4 文中算法在MNIST数据集的加速比 图5 文中算法在MNIST数据集的扩展比 Fig.4 Speedup ratio of proposed algorithm in MNIST data set Fig.5 Expansion ratio of proposed algorithm in MNIST data set

3.4 可视化效果和精确度

对高维数据集进行降维处理，最终将其可视化于二维空间，点的颜色对应不同的对象类别.通过准确率、召回率和相对准确率衡量算法的精确度.

准确率ξP和召回率ξR的计算公式分别为

(16)

(17)

式(16)，(17)中：Ng，h为属于g类，但被划归到h类中的数据数量；Ng为g类中的全部数据数量；Nh为h类中的全部数据数量.

由此可得精确度的评价指标相对准确率ξF为

(18)

为了验证文中算法的可视化效果和精确度，采用t-SNE算法(单机环境)，基于Spark平台的t-SNE算法(和文中算法环境相同)、文中算法在BREAST CANCER，MNIST和CIFAR-10数据集上进行实验，其可视化效果对比，如图6～8所示.图6～8中：Ex，Ey分别表示原始数据的两个特征值.

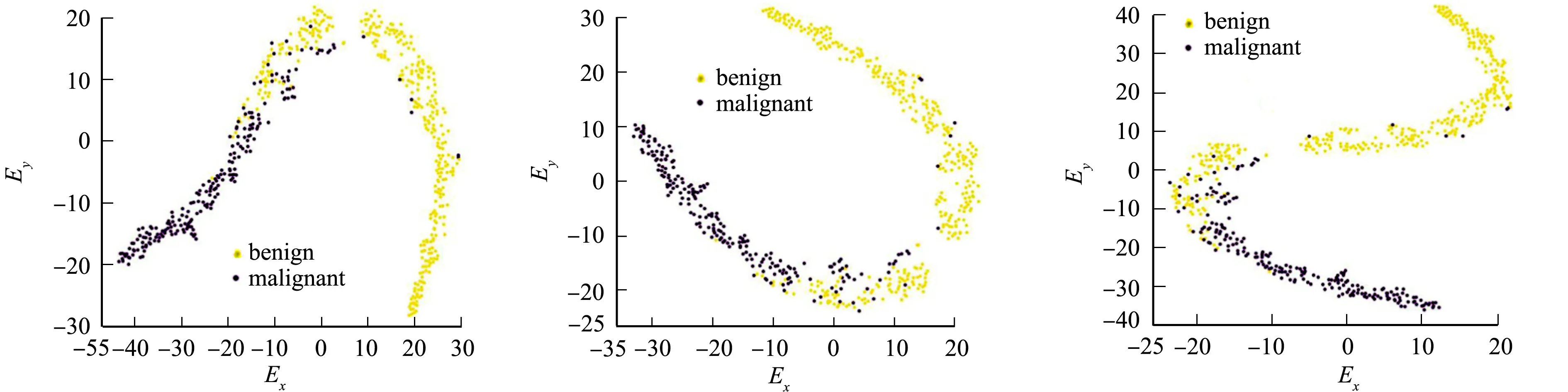
(a) t-SNE算法 (b) 基于Spark平台的t-SNE算法 (c) 文中算法图6 3种算法在BREAST CANCER数据集上的可视化效果对比Fig.6 Comparison of visualization effects of three algorithms in BREAST CANCER data set

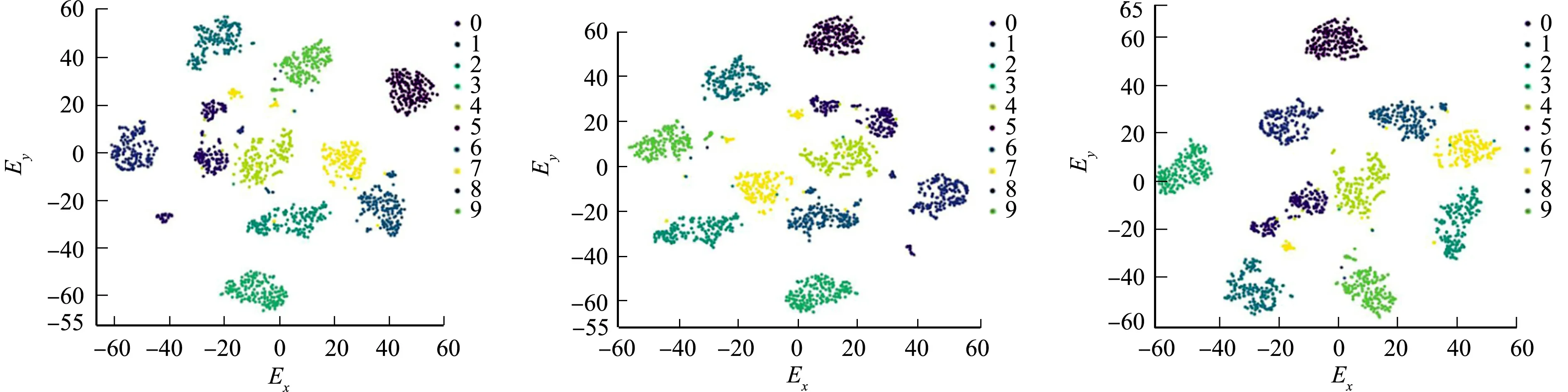
(a) t-SNE算法 (b) 基于Spark平台的t-SNE算法 (c) 文中算法图7 3种算法在MNIST数据集上的可视化效果对比Fig.7 Comparison of visualization effects of three algorithms in MNIST data set

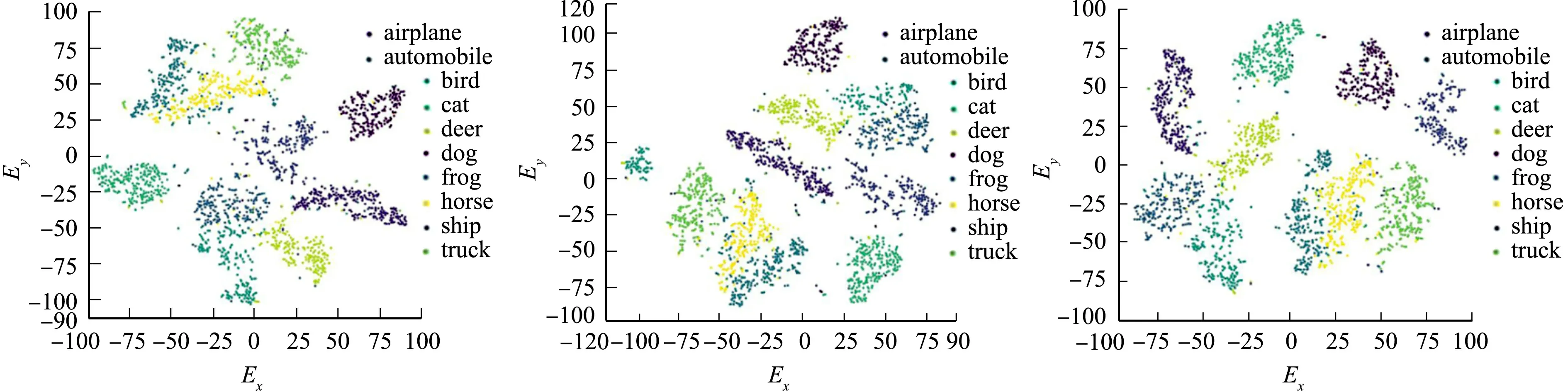
(a) t-SNE算法 (b) 基于Spark平台的t-SNE算法 (c) 文中算法 图8 3种算法在CIFAR-10数据集上的可视化效果对比Fig.8 Comparison of visualization effects of three algorithms in CIFAR-10 data set

由图6～8可知：原始BREAST CANCER数据集是30维的向量，有效映射到二维散点图被分为2类；原始MNIST数据集是784维的向量，有效映射到二维散点图被分为10类；原始CIFAR-10数据集是1 024维的向量，有效映射到二维散点图被分为10类.

不同数据集的精确度对比，如表1所示.

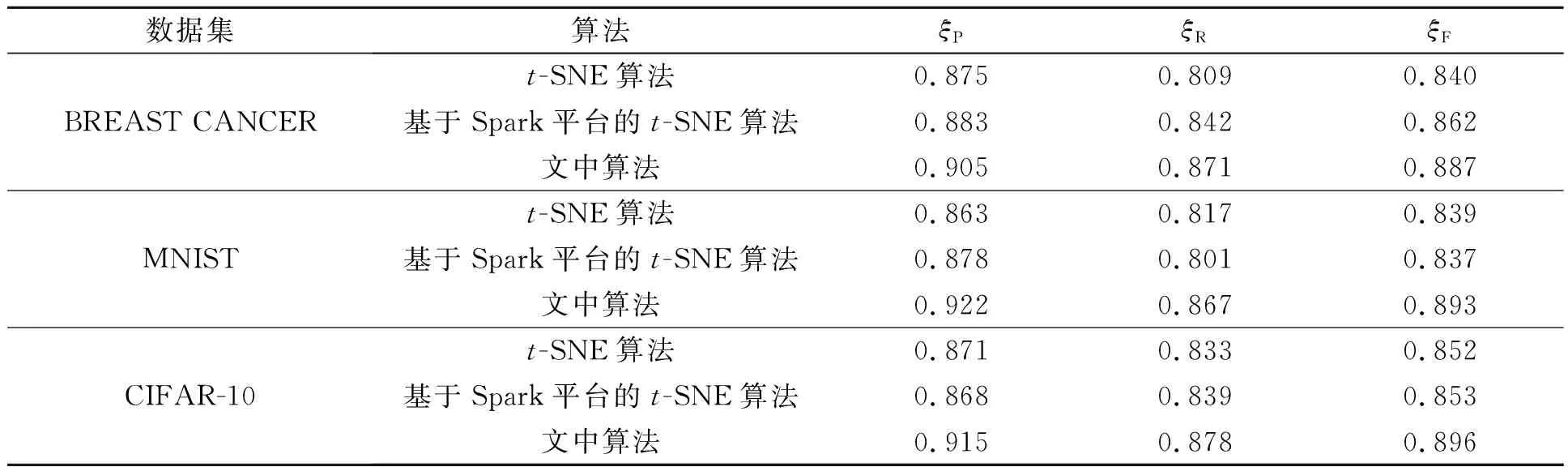
表1 不同数据集的精确度对比Tab.1 Accuracy comparison of different data sets

由以上分析可知：文中算法在降维后的可视化效果、准确率、召回率和相对准确率均明显优于其他两种算法.

4 结束语

提出一种结合PCA的t-SNE算法的并行化方法.在MNIST数据集中，对文中算法进行实验，验证了文中算法在大规模数据集中可以在提高运行效率和精确度的前提下，高效地完成降维可视化.然而，降维会使数据被映射到低维空间时产生错误位置，导致其附近信息的丢失，原始高维空间中一些特征未能得到较好的保留.此外，通过保留数据的周围信息，将数据从高维空间映射至低维空间，并未考虑全局数据之间的关系.虽然文中算法能够在Spark平台下对大规模数据集进行处理，但由于文中算法是将低维数据作为变量进行迭代，一旦更新数据，需要重新启动算法，因此，在灵活性和开销方面仍有不足，今后将针对该问题开展相关研究.