考虑时空距离的低值可回收物收运路线优化

□ 张 慧

(上海理工大学 管理学院,上海 200093)

1 引言

2021年5月6日，国家发展改革委、住房城乡建设部下发《“十四五”城镇生活垃圾分类和处理设施发展规划》强调，推动低值可回收物的回收和再生利用。随着消费水平不断提升，垃圾数量正以平均每年10%-15%的速度增长[1]，“垃圾围城”成为亟需解决的环境问题。产生该问题的主要原因是生活垃圾中掺杂大量低值可回收物。据中国环保在线统计，我国年产生活垃圾中有27%为可回收部分，剩下73%的垃圾中有40%是低值回收物[2]。由于收运成本过高，低值可回收物无人问津。较低回收率不仅会造成资源流失，还会污染环境。因此，有必要优化收运路线。

生活垃圾收运路线优化一直是国内外研究的热点，部分学者进行了相关的研究。João Teixeira等[3]运用启发式算法求解车辆服务的地理范围，每天的收集废物类型、收运路线。结果表明，安排收集计划可大幅度节约成本。Afroditi Anagnostopoulou等[4]优化收集服务的路线，节约总收运时间和能源消耗。张爽等[5]考虑垃圾量不确定因素，构建居民满意度的生活垃圾上门收运路线优化模型，采用人工鱼群算法求解出最短路径。王晨頔等[6]在调度模型中加入车辆中转站排队等待的时间，考虑工作量、清运时间两方面，建立以成本最低为目标的模型。符俊波等[7]为解决垃圾清运量变化引起的干扰问题，分析收运车辆的扰动辨识，建立调整后的方案与原方案误差最小的数学模型。目前，关于低值可回收物的研究聚焦于政府经济激励层面。杜欢政等[8]从收集、运输、分拣三个环节确定各品类低值废物的成本和收益后，核算不同利润率下政府的补贴金额。杜欢政等[9]采用政府节约综合选择法计算回收低值可回收物的政府补贴，与“一刀切”式相比，该方法能降低支出。蒋南青[10]对低值可回收物的源头收集，提出不同的奖励方式。

综上，生活垃圾收运路线优化的研究十分丰富，对低值可回收物的研究需要进一步探索。因此，本文以收运成本最低为目标，构建考虑时空距离的两级车辆路径优化模型。

2 问题描述与符号说明

2.1 问题描述

两级收运路径问题描述如下：二级收集车辆从中转站出发，通过既定的路线为居民服务，待完成全部收运任务后，返回中转站。在中转站，低值可回收物被转移到一级运输车辆，完成后返回集散中心。在收集过程中，因路况或服务时间窗更改等原因，居民可接受车辆提前或延迟到达收集点。需解决的问题是合理规划路线，最大程度降低成本。

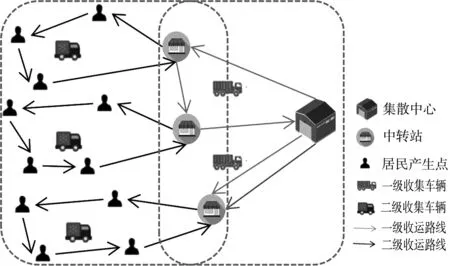
图1 两级收运路线结构图

2.2 模型假设

①收集、运输车辆的单位运输成本已知；

②中转站和居民的数量、地理位置已知；

③收集车辆、运输车辆的装载容量已知。

2.3 符号说明

集合：

D：集散中心，D ={0}

S：中转站集合，S ={1,2,…,s}

C：收集点集合，C ={1,2,…,n}

B：一级运输车辆集合，B ={1,2,…,b0}

K：二级收集车辆集合，K ={1,2,…,k0}

指标和参数：

i/j：居民点、中转站节点索引

QB：运输车辆的容量

QK：收集车辆的容量

FB：运输车辆固定成本

FK：收集车辆固定成本

a1：运输车辆单位运输费用

a2：收集车辆单位运输费用

dij：节点i，j间的距离

qi：收集点i的收集量

Lbij：车辆b在弧 (i,j) 之间装载量，b ∈ B

Lkij：车辆k在弧 (i,j) 之间运输量， k ∈ K

tki/tkj：车辆k到达i或j的时间，k ∈ K

tkij：车辆k从节点 i 驶向节点 j 的时间

tkdi：车辆k在居民点i的等待时间，k ∈ K，i ∈ C

tksi：车辆k在居民点i的服务时间，k ∈ K，i ∈ C

[ETi，LTi] ：收集点i ∈ C的期望时间窗

c：收集点单位时间窗偏离量费用

决策变量：

xijb：0-1 变量，若车辆b通过弧(i,j)，则为1，否则为0；

yijk：0-1 变量，若车辆k通过弧(i,j)，则为1，否则为0；

zik：0-1 变量，若i点由车辆 k 收集，则为1，否则为0。

3 模型构建

3.1 目标函数

目标函数包括车辆固定成本(Z1)、运输成本(Z2)、车辆未在期望时间窗内到达的惩罚成本(Z3)，三者之和成本最少。

Min=Z1+Z2+Z3

(1)

(2)

(3)

(4)

3.2 约束条件

(5)

一级运输车辆的容量约束；

(6)

确保每个中转站最多只能被服务一次；

(7)

保证一级收运网络中每个节点的进出车辆相同；

(8)

二级收集车辆的容量约束；

(9)

保证每个收集点被一辆收集车辆服务一次；

(10)

保证二每个节点进出车辆相同；

(11)

车辆载重量守恒约束；

(12)

确保所有车辆空车返回其原始集散中心或中转站；

(13)

计算收集车辆的等待时间；

tkdi=max[(ETi-tki)zik,0],∀i∈C,k∈K

(14)

计算车辆到达节点j∈C的时间

(15)

3.3 求解收运路线算法介绍

由于居民点较多，第二级收集路线采用考虑时空距离的改进模拟退火算法，第一级节点数量较少，采用精确方法。

①考虑时空距离的初始路径规划。

一般车辆路径问题用空间距离衡量远近[11]。实际中，服务时间窗接近，位置相隔较远，不适宜规划在同一路径上。因此，本文采用时空距离度量收集点间时间加空间的远近关系。

(16)

欧式距离描述i(xi,yi)和j(xj,yj)之间的空间距离。

(17)

假设[a,b]和[c,d]是居民点i,j预约的时间窗。不妨令a≤c，若收集车到达点i的时间为t∈ [a,b],si是服务时间，tij是指点i到点j花费的路由时间，则到达j的时间为t′∈ [a′,b′],其中：a′=ei+si+tij，b′=li+si+tij

提前或超过规定时间窗的，增加相应惩罚系数。根据提前、准时、延后到达居民点三种情况，i点与j点之间时间距离为：

(18)

②初始解优化。

改进模拟退火算法是在传统基础上，加入变邻域搜索算法、交换算子，两种变换：变换1 某条路线中的一个收集任务插入到另一条路线中；变换2 某两条路线中两个居民点的收集任务互换。

4 算例研究

4.1 算例数据

拟选取80个低值可回收物产生点，表1中xi为收集点横坐标，yi为收集点纵坐标，Qi为收集量(单位：t)，[ETi，LTi] 收集点i的期望时间窗。专家筛出中转站1、2、4和集散中心2、3，。单位运输成本(元/t.km)分别为2.5,4.3,6.3；车容量(t)QB为4000、QK为300；车辆固定成本(元)FB为500、FK为100；单位运输费用(元)a1为18.5、a2为2.5；收集点单位时间窗偏离量费用(元)c为0.1；

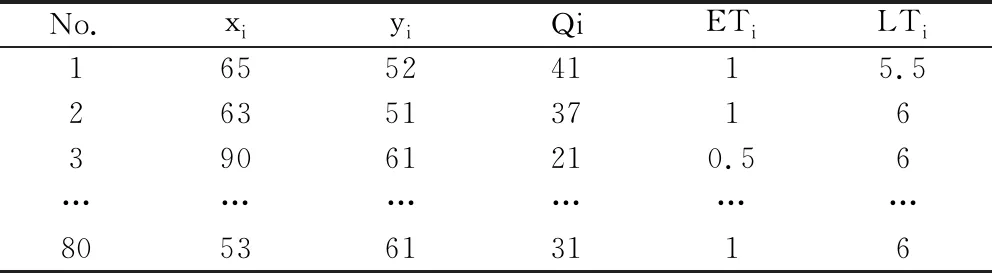
表1 收集点、中转站、集散场位置

4.2 算例结果

共有80个收集点，3个中转站。运用改进模拟退火算法-时空距离、模拟退火算法、变邻域搜索算法、改进模拟退火算法求解收运路线，最优值结果如表2。

表2 四种算法求解结果对比表

由表2可看出，考虑时空距离的改进模拟退火算法计算目标函数值最低，成本降低了225.06。收敛过程如图2所示。

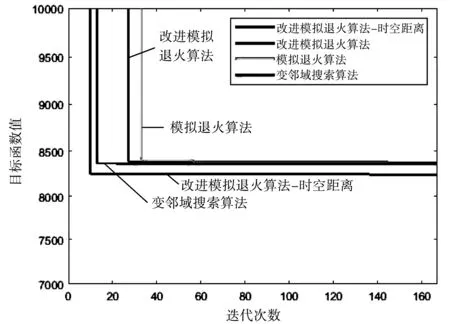
图2 四种算法收敛过程对比

由图2可知，初始阶段，改进模拟退火—时空距离算法由于接受较差解的概率较大，第12次迭代时开始迅速下降，速度超过其他三个算法，最终收敛得到的总收运成本最好。四个算法中收敛速度最慢的是模拟退火算法，最终结果最差。

4.3 两级收运路线优化结果

考虑时空距离的改进模拟退火算法求解两级收运路径的收运成本和惩罚成本，结果如表3。

表3 两级车辆路径相关成本

由表3计算可得，第一级收运路线成本为3066.05元，第二级收运成本为8733.53元，所需一级车辆数2辆，二级车辆数12辆。两级收运路线如下：

第二级收集路线：

1：中转站4→29→2→73→65→9→13→4→63→68→中转站4

2：中转站4→45→50→6→42→17→14→23→27→71→中转站4

3：中转站4→78→25→75→20→10→57→3→中转站4

4：中转站4→15→8→21→56→22→34→28→54→中转站4

5：中转站2→36→77→48→中转站2

6：中转站2→67→60→19→69→76→39→38→中转站2

7：中转站2→66→41→30→72→16→47→5→62→中转站2

8：中转站4→35→53→31→80→18→24→55→中转站4

9：中转站1→26→79→11→33→59→46→51→中转站1

10：中转站2→7→61→32→74→43→中转站2

11：中转站1→44→64→52→1→37→49→40→中转站1

12：中转站4→12→70→58→中转站4

第一级运输路线：

1：集散中心2→中转站2→集散中心2

2：集散中心3→中转站1→中转站4→集散中心3

5 结语

本文对低值可回收物回收路径优化问题展开了研究，建立了多中心、软时间窗模型，在此基础上设计了一种考虑时空距离的改进模拟退火算法。算例结果表明：①考虑时空距离的改进模拟退火算法能够大幅度提高求解质量及速度,②两级收运成本为13865.63元，降低了225.06元。

当前研究还存在一些有待改进的地方,例如:未考虑低值可回收物收运过程中出现的服务时间窗变动、回收量变化、新增订单等干扰事件，后续可针对该方面展开一定的研究。