基于统计过程控制的建筑沉降监测分析方法
王熠琛, 张明聚, 李立云, 卢鑫月
(北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124)
城市地下工程的开挖会扰动周围岩土体,导致邻近建筑产生沉降变形[1]. 为保证建筑的安全可靠,施工中必须对沉降进行监测分析,从而采取工程措施降低沉降产生的不利影响[2-3].
现阶段的沉降监测分析以总体沉降与差异沉降为核心,每项监测量以变化量与变化速率为控制指标,即双控指标[3-4]. 已有研究重点关注双控指标的阈值,基于工程经验标准[5-7],结合数值模拟[3,4,8-10]与模型实验[5,11]确定阈值大小;并基于最大监测量与阈值之比明确工程措施. 这种分析方法具有科学合理性且易操作,但也存在不足. 首先,该方法主要关注沉降演化过程的最大监测量,对整体性考虑不充分;其次,该方法采取确定性分析思路,对动态数据的随机性考虑不足. 因此,为使工程决策更科学,需要优化分析方法.
统计过程控制(statistical process control,SPC),基于统计推断理论分析过程反馈的信息,采取控制措施,确保过程处于稳定的受控状态. 该技术可以分析过程的整体信息,并能考虑信息数据的动态随机性,使分析过程更科学. 实践表明,二战后日本在民用工业中广泛使用SPC技术,使得生产效率快速提升,促使战后经济快速恢复[12]. 在土木工程领域,SPC技术主要用于桥梁等大型结构的健康监测[13-15],以及工程建设材料与施工质量的监控[16-18]. 然而在地铁等岩土工程的监测分析中,SPC技术的应用实例还比较少.
为了优化现阶段的沉降分析方法,本文引入SPC技术提出一种新的分析方法,并选择北京地铁8号线某典型的隧道区间进行实例分析,初步验证引入SPC技术的合理性与优势.
1 SPC的原理与思路
SPC以过程反馈的动态信息数据为分析对象. 它认为数据的动态变化分为两部分,一部分是随机因素引起的正常波动,另一部分是系统因素引起的趋势性变化. 若一个过程仅受随机因素影响,则认为该过程处于稳定受控状态. 若一个过程受到系统因素影响,则认为该过程处于不稳定与不受控状态. SPC首先利用统计推断理论分析数据的变化特征,从而识别过程是否处于稳定受控状态;再根据数据的统计特性判断过程维持的性能状态,从而决策出过程需要采取的控制措施.
1.1 统计控制图
统计控制图(statistical control chart,SCC)作为SPC的核心工具,用于分析识别过程的稳定受控性. 它由二维坐标系与3条水平线组成,其中横坐标代表过程的时间点,纵坐标代表与过程信息数据相关的统计量;3条水平线分别为上控制线、中心线与下控制线.
SCC认为如果过程处于稳定受控状态,那么与该过程相关的动态监测量应服从正态分布,即正态性假定.数据若服从正态分布N(μ,σ2),那么其落入区间(μ-3σ,μ+3σ)的概率为99.73%,落入区间(μ- 3σ,μ+3σ)外的概率仅为0.27%.由于小概率事件被认为通常不发生,因此若动态监测量落在区间(μ-3σ,μ+3σ)之外,则认为过程处于不稳定与不受控状态.此观念即为3σ质量控制准则,其核心思想是如果某一过程处于稳定受控状态,那么相关的动态监测量应维持在(μ-3σ,μ+3σ)区间内.
SCC是根据正态性假定与3σ质量控制准则所构造.它首先计算出监测量在各时间点上的统计量,并将其绘制在二维坐标中.然后计算出所有统计量的均值μ与方差σ,进而确定下控制线、中心线、上控制线,它们的纵坐标点分别对应于μ-3σ、μ、μ+3σ.通过对比每个时间点上的统计量与控制线的关系,即可识别出过程的稳定受控性.
1.2 过程能力指数
过程能力指数(process capacity index,PCI)用于计算一个过程所具备的能力大小,进而判断一个过程所维持的性能状态.它的基本形式为
(1)
式中:B代表实际监测量统计分布范围,由实际监测数据的分布特征确定;D代表实际监测量相对某一性能状态的阈值能够允许的分布范围,由阈值形式与数值计算确定;D与B的具体计算步骤详见后续第3节.CP即为PCI,其越大意味着监测量的允许分布范围越大于其实际分布范围,说明过程维持状态的能力越强.
由于PCI的计算基于监测量的统计分布范围,根据正态性假定,基于PCI的大小还可以计算出过程维持某一状态的失效概率.
SPC可以综合监测数据的SCC特征与PCI的数值,对过程进行动态分析与控制.不仅要求过程具备维持某一性能状态的能力,而且要求过程维持在仅受随机因素影响的受控状态下.
2 基于SPC的监测分析流程
基于现阶段沉降监测分析方法的原则,引入SPC技术建立新的监测分析方法,并提出新方法的具体流程与步骤.
2.1 分析方法的基本思路
基于现阶段分析方法的原则,以建筑总体沉降与差异沉降2项监测量为核心,认为监测量数值过大或出现不稳定变化时,需采取控制措施.引入SPC技术,则利用统计推断理论,按照如下2个方面分析识别监测量的大小与变化特征.
1) 沉降监测量变化特征的识别
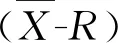
2) 沉降控制能力的分析
根据实际工程确定总体沉降与差异沉降的控制阈值,计算沉降监测量的PCI.PCI定量表征相对于阈值建筑沉降变形的控制能力,PCI的值越大则控制能力越强.
综合上述2个方面的分析,按照表1的准则确定相应沉降控制措施,并合理更新后续时段的监测数据,动态分析整个沉降演化过程.
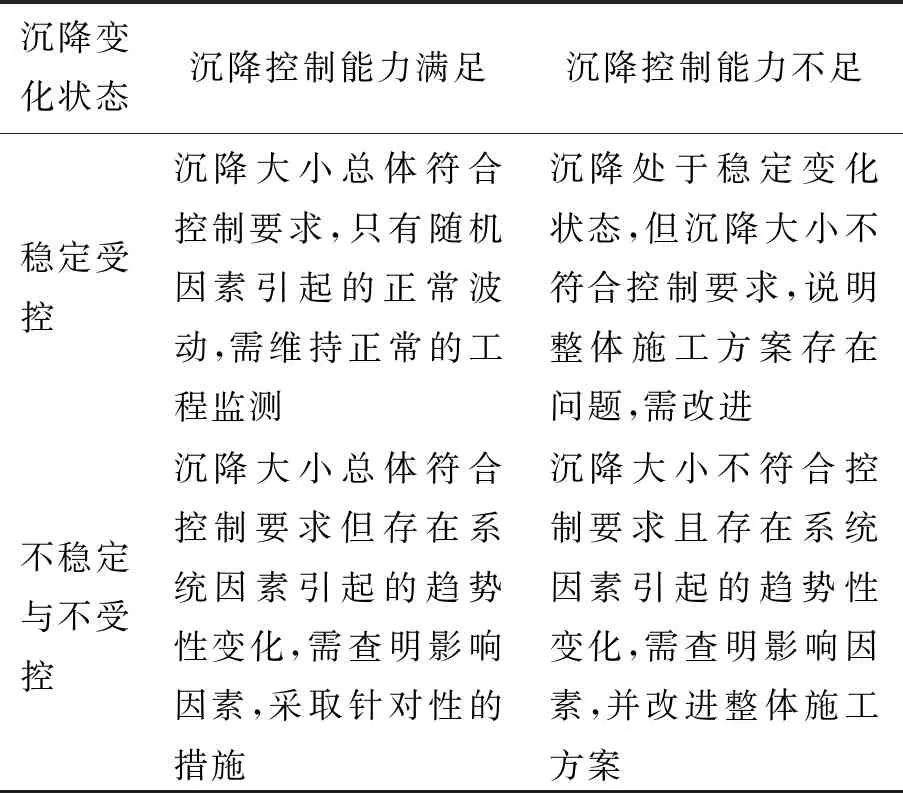
表1 基于SPC的建筑沉降控制准则
2.2 分析方法的具体流程
1) 沉降监测数据的采集
根据邻近建筑物的种类、规模以及构造等特征,参考相关的工程经验与监测规范,选择合理位置布置沉降监测点.按照具体要求与监测频率进行监测,确保所采集监测数据的准确与可靠,数据量与精度需满足实际工程的要求.
2) 建立监测数据的SCC
3) 计算监测数据的PCI
根据建筑的特征参考相关工程规范,确定建筑的沉降控制阈值.计算沉降监测数据相对于阈值的PCI,确定沉降变形的控制能力是否充足.
4) 明确沉降控制的工程措施
综合SCC与PCI计算结果,按照表1的准则进行工程技术的管理与决策.整个施工过程的沉降监测分析流程如图1所示.

图1 建筑沉降监测分析流程
3 建筑沉降监测的分析模型
为便于新方法在实际应用中的计算机编程,所建模型以矩阵形式呈现.模型由如下几个重要部分组成.
3.1 变化特征识别模型
1) 选择初始时段的监测数据,以矩阵MS(t0) 的形式呈现,即

(2)
式中:t0代表第0时段即初始时段;mij(t0)代表该时段内第i个监测点在第j个时间点上的沉降监测量.
2) 计算每个时间点上监测量的极差与均值,有
(3)
式中:rj(t0)与aj(t0)分别代表该时段内第j个时间点上沉降监测量的极差与均值.


(4)

4) 根据各时间点上监测量的统计量以及各个控制线的坐标值,即可建立监测量的SCC.通过对比SCC中各时间点上统计量与控制线的关系,即可识别出建筑物的总体沉降与差异沉降是否处于稳定受控状态.基于SCC分析的基本原理,得到沉降变化特征识别模型

(5)
式中VC(t0)与VZ(t0)分别表示该时段内差异沉降与总体沉降变化特征的识别结果.
3.2 控制能力分析模型
1) 计算差异沉降量相对于控制阈值的PCI,计算公式为
(6)
式中:rd(t0)与ra(t0)分别表示该时段内各时间点沉降量极差的标准差与算数平均值;CYC表示差异沉降的控制阈值,由规范与经验确定;由于阈值只存在上界,因此DC(t0)表示在考虑沉降控制上限的前提下差异沉降的允许分布范围,而BC(t0)表示实际差异沉降的统计分布范围,CPC(t0)则表示该时段内差异沉降控制的PCI.
2) 计算总体沉降量相对于控制阈值的PCI,计算公式为
(7)
式中:ad(t0)与aa(t0)分别表示该时段内各时间点沉降量均值的标准差与算数平均值;CYZ表示总体沉降的控制阈值,由规范与经验确定;同理,由于阈值只存在上界,因此DZ(t0)表示在考虑沉降控制上限的前提下总体沉降的允许分布范围,BZ(t0)表示实际总体沉降的统计分布范围,CPZ(t0)则表示该时段内总体沉降控制的PCI.
3) 根据PCI,建立沉降控制能力的分析模型
(8)
式中沉降控制能力大小的判断依据是由PCI转换来的失效概率.CPZ<1时失效概率大于0.27%,认为控制能力不足;当CPZ为1~4时,失效概率小于0.27%,认为控制能力满足要求;CPZ>4时失效概率为0,认为控制能力充足.
3.3 动态监测分析模型
根据分析结果采取合理的沉降控制措施,并更新数据,对后续时段的沉降监测数据进行持续的动态分析,分析模型为
(9)
式中:VC(tk)与VZ(tk)分别表示第k时段内差异沉降与总体沉降的稳定受控性;CPC(tk)与CPZ(tk)分别表示第k时段内差异沉降与总体沉降的受控能力.
4 工程实例分析
本节选择北京地铁8号线三期项目中一隧道区间段,利用所提出方法进行工程实例分析.该区间段邻近一古建筑,重要性等级较高,具有一定的代表性.该工程案例为已建设完成的项目,分析沉降监测数据的目的并不是要指导施工,而是基于对沉降演化的模拟分析验证新方法.
4.1 工程概况
所选工程案例来源于北京地铁8号线天桥—永定门外隧道区间,该隧道区间采用左右双线盾构施工方式,隧道自天桥站开始向南开挖掘进,先后要穿越或邻近多个重要工程设施.在右线隧道里程段K34+ 793.7~K34+ 818.6处,隧道邻近古建筑燕墩.燕墩为始建于元朝的烽火台,坐落于老北京城南北中轴线的南侧,属于北京市级文物保护建筑,具有历史文化价值.燕墩为砖石材料构造的正方形墩台,其边长约为15 m,位于右线隧道的西侧,距离右线隧道的最近水平距离为7.9 m,见图2.

图2 工程项目的平面图(单位:m)
此里程段内,左右两线隧道间距为 16.63~17.08 m.隧道上方道路地表到隧道拱顶的覆盖层厚度约为22 m,燕墩四周地平面到隧道拱顶的垂直距离约为28 m,见图3.盾构施工过程中,管片的宽度为1.2 m.其中里程段K34+793.7~K34+818.6对应管片为第797~818环.工程进度显示,在右线盾构掘进至第738环时,为保证燕墩的安全可靠开始进行沉降监测;监测开始第16天,盾构掘进至第797环,开始进入K34+793.7~K34+818.6里程段;第26天,盾构掘进至第817环,即将穿越里程段K34+793.7~ K34+818.6;第26天后,盾构掘进穿越里程段K34+793.7~ K34+818.6.

图3 工程项目的立面图(单位:m)
盾构掘进穿越里程段K34+793.7~K34+818.6的过程中,对燕墩采取沉降控制与保护措施.包括加大注浆量、管片加强、严格盾构机选型与刀盘配置、合理选定盾构机参数等.
4.2 沉降监测初步分析
1) 测点布设
为了有效对燕墩进行沉降控制,施工过程中在燕墩四周布置了相应的沉降监测点.本文选取的沉降监测数据来源于4个关键测点,测点分别位于燕墩平面的4个角点上,见图4.

图4 沉降测点位置分布(单位:m)
测点的监测频率为1次/d,测量精度为0.3 mm,所采用测量仪器的分辨率为0.01 mm.所采集监测数据表示各个测点每天沉降监测量的大小,即以天为单位,共有37天.
2) 采集监测数据
采集到4个测点的沉降监测数据以及建筑的差异沉降量,以时程图表示见图5.

图5 沉降监测值时程图
3) 沉降监测的传统分析法
传统方法以双控指标为核心,即控制沉降大小与沉降变形速率.该项目实际建设过程中沉降控制指标主要包括:建筑各测点的沉降量、建筑差异沉降量、沉降变形速率.根据各指标的控制阈值与最大监测量大小,其分析结果见表2.

表2 沉降监测分析
分析结果表明,地铁施工过程中所有的沉降控制指标都没有超过阈值,开挖引起燕墩的沉降变形总体处于安全状态.时程图中第10~25天时间点内对应盾构施工接近并逐渐穿越里程段K34+793.7~K34+818.6的过程,该时段内各测点沉降与差异沉降监测量都出现了明显的增长趋势.
接下来将采用新方法进行数据分析.
4.3 初始阶段的监测分析
1) 选择初始阶段的沉降监测数据,按照式(2)~(4)的方式计算SCC的坐标值.
(10)
根据计算的坐标绘制SCC,见图6.

图6 初始阶段的SCC
根据SCC和式(5)即可得到沉降变化特征的识别结果
(11)
2) 按照式(6)(7)计算差异沉降与总体沉降的PCI,有
(12)
根据式(11)(12)的计算结果得到初始时段的沉降监测分析结果
(13)
3) 根据式(13)的结果可以明确,初始阶段内建筑的差异沉降与总体沉降都处于稳定受控状态,且沉降控制能力充足,需维持正常监测.
实际工程中,此时段内盾构开挖距里程段K34+793.7~K34+818.6的距离约为35 m,开挖对燕墩的影响较轻微,表明SPC可分析出合理结果.
4.4 后续阶段的动态监测分析
实际地铁施工中如果按流程分析数据,随着数据更新上述的分析过程需要被重复执行.由于篇幅限制,本文只呈现几个代表性的时段.
1) 第5次数据更新时段
重复上述步骤绘制SCC,见图7.

图7 第5次更新时段的SCC
按式(6)(7)计算差异沉降与总体沉降的PCI,从而得到该时段内的沉降监测分析结果
(14)
式(14)的分析结果表明,第5次数据更新时段内建筑差异沉降处于稳定受控状态,总体沉降处于不稳定与不受控状态,其控制能力完全充足.虽然沉降控制符合要求,但沉降受系统因素的影响发生了趋势性变化,需采取针对性的工程措施.
实际工程中,在此时段内盾构开挖即将进入里程段K34+793.7~K34+818.6,开挖对燕墩造成明显的影响.虽然沉降变形量不大,但SPC可准确识别出沉降发生的趋势性变化,并根据分析结果对拟执行的工程措施作出合理决策.
2) 第16次数据更新时段
重复上述步骤绘制SCC,见图8.
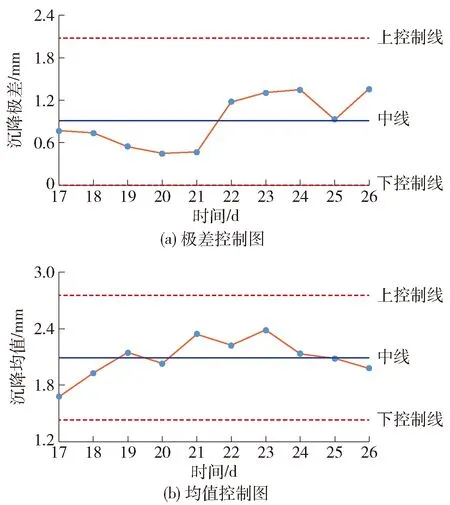
图8 第16次更新时段的SCC
按式(6)(7)计算差异沉降与总体沉降的PCI,得到该时段内的沉降监测分析结果
(15)
式(15)的分析结果表明,第16次数据更新时段内建筑差异沉降与总体沉降都处于稳定受控状态,差异沉降控制能力满足要求,而总体沉降控制能力充足,需维持正常监测.
实际工程中,在此时段内盾构开挖即将穿越里程段K34+793.7~K34+818.6,由于穿越过程中采取了沉降控制与防护措施,因此燕墩的沉降变形逐渐趋于稳定.SPC可准确识别出沉降的变化是否趋于稳定,从而明确所采取工程措施的有效性.
3) 后续数据更新时段
重复上述步骤绘制SCC,见图9.由于上一时段内沉降变化已经处于稳定与受控状态,因此只需延长SCC中的上控制线、中心线与下控制线,对后续阶段的沉降监测数据进行持续分析.

图9 后续时段的SCC
SCC分析结果表明,后续时段内建筑差异沉降与总体沉降都处于稳定受控状态,建筑的沉降变形已趋于稳定,沉降控制达到要求.
实际工程中,在此时段内盾构开挖已完全穿越里程段K34+793.7~K34+818.6,穿越过程采取的沉降控制与防护措施保证了沉降变形的稳定性.分析结果再次说明,SPC可通过对沉降变化特征的识别判断所采取工程措施的有效性.
4.5 工程实例分析总结
工程实例分析验证了本文所提出分析方法的合理性与优势,表现为如下几方面.
1) 对沉降演化的分析符合地铁施工诱发沉降变形的基本规律.在初始时段,盾构施工与建筑物距离较远,所提出分析方法能识别出沉降处于稳定受控状态且控制能力充足.而在第5次更新时段,盾构施工已临近建筑物,所提出分析方法能识别出沉降处于不稳定与不受控的状态.
2) 可以合理决策出拟执行的沉降控制措施.在第5次更新时段,沉降整体变形还较小,但SPC可明确识别沉降变形已处于不稳定与不受控状态,从而进行相应的管理与决策.
3) 可对所执行措施的有效性进行科学验证.在第16次更新时段与后续时段,盾构施工已穿越建筑临近区域,穿越过程采取了沉降控制与防护措施.SPC可明确识别沉降变形处于稳定受控状态,从而判别出所采取工程措施的有效性.
5 总结与展望
针对地铁施工中邻近建筑物沉降监测分析方法的不足,引入SPC技术对其优化,从而提出新的分析方法并建立相应的计算模型.利用工程实例进行检验,验证了引入SPC技术的合理性与优势.
5.1 引入SPC技术的优势
1) 以沉降演化过程的整体数据为分析对象,基于统计推断理论可以合理分析过程演化的动态随机性,以弥补传统分析方法的不足.
2) 采用SCC与PCI识别与分析沉降变化特征与沉降控制能力,不仅可以合理决策出沉降控制措施,而且可以对现有执行措施的有效性进行科学验证,这点是SPC的明显优势.
3) SPC紧密结合概率统计理论,可对监测数据进行科学的不确定性分析,符合城市地下工程建设风险管理理念的要求.
5.2 SPC技术推广应用的展望
1) SPC的主要理论依据为正态性假定,然而在土木工程领域有时候工程参数与指标并不满足正态性假定需求.如何利用统计检验法优化SPC的分析过程,是后续研究的主要方向.
2) SPC以统计推断理论为基础,对数据量有一定要求,测点数量过少或监测频率过低都会导致不利影响.所以SPC的推广应用必须依赖现代化的信息技术,确保数据的数量与时效要求.
3) SPC的分析过程随着数据的更新需进行大量重复计算,所以SPC的推广应用必须借助计算机编程,需开发软件进行快速的计算与分析.

