基于声弹性效应的螺栓轴向应力检测方法

吕 炎， 谢龙扬， 宋国荣， 何存富， 程 俊， 毛延翩， 姬升阳

(1.北京工业大学材料与制造学部， 北京 100124； 2.溪洛渡水力发电厂， 云南 昭通 657300)

螺栓是一种常用的联接件，它被广泛地应用在机械设备、航天、工程建筑、交通工具、仪器仪表等领域[1]. 螺栓轴向应力大小，将直接关系到整个设备或结构的安全性和可靠性，同时对螺栓自身的性能和寿命也有较大的影响. 设备或结构在服役过程中，会受到温度变化、载荷大小变化、振动等各种外部因素的影响，导致螺栓轴向应力发生变化，最终可能对设备和结构造成巨大破坏. 螺栓在拧紧过程中，若预紧力过大可能会导致疲劳破坏，发生断裂现象，甚至导致设备故障或结构失稳；若预紧力过小可能导致结构联接不可靠，易发生振动松弛、滑移等状况，影响工作的正常进行[2]. 因此，精确测量螺栓轴向应力已成为各工程领域亟待解决的重要科学问题之一，对保障国民生产安全具有重大的意义[3].

目前常用的螺栓轴向应力检测方法有扭力扳手法、电阻应变片法、连续波法和超声脉冲回波法等. 其中，扭力扳手法是一种最普遍的测量和控制螺栓轴向应力的方法，该方法操作简单，但是测量误差较大，难以满足高精度检测需求的工程[4]. 电阻应变片法通过测量受力后螺栓表面的应变，来检测螺栓轴向应力的大小. 但该方法必须将应变片贴在螺栓受力段的侧面，且只能检测螺栓表面的应力，在实际应用中的局限性较大[5]. 连续波法是将螺栓看作一个谐振体，施加在螺栓上的应力与其机械谐振频率呈线性关系，通过测量频率来得到螺栓轴向应力大小. 这种方法的缺点在于螺栓的两端都需要设置探头，在实际工程中的可行性不高[6].

超声波检测作为一种无损检测与评价的常用方法，具有节能环保、高度集成化、精度高、便携化、快速高效等优点，应用前景十分广阔. 超声波检测应力是一种间接的测量方法，通过测量超声波渡越时间(time-of-flight, TOF)来间接获取螺栓的轴向应力. 渡越时间即为超声波在螺栓轴向方向上传播的往返时间. 超声检测法的理论基础是弹性固体存在声弹性效应，即超声波传播速度随应力状态变化而改变的现象[7].

目前，采用超声法对螺栓轴向应力进行检测的方法主要为纵波法和纵横波结合法. 纵波法的优势在于操作简单且测量精度高，但该方法需要对螺栓无应力状态下的渡越时间进行检测，而在实际工程中螺栓一般都已经投入使用，处于紧固状态，所以很难获得无应力状态下螺栓的渡越时间. 纵横波结合法是为了克服纵波法的缺点而提出的，其原理为分别测量螺栓在受应力状态下横波和纵波的渡越时间，通过比值运算来求得螺栓轴向应力. 纵横波结合法的优点在于不需要对已经安装的螺栓进行拆卸测量，在实际工程中有更好的可操作性，同时也适用于进行长期监测[8].

为了更好地解决实际工程中的螺栓轴向应力检测问题，本文采用纵横波结合法展开理论推导和实验研究. 纵横波结合法测量螺栓轴向应力的发展已有很长的历史. 1988年，吴克成等[9]利用基于声弹性效应的纵横波相结合技术，并建立新的材料常数M，这样就无须知道无应力状态时超声波在螺栓内的渡越时间，为将该技术应用于实际工程奠定了基础. 1990年何存富[7]从理论和实验两方面研究了温度对超声螺栓应力检测的影响，测定了纵横波传播时间与温度的修正曲线，并对九江大桥高强螺栓进行了群栓实测实验，取得了良好的效果. 随着技术的发展，Hirao等[10]提出了非接触式测量，并研制出了一套能够同时发射纵波和横波的设备，提高了超声螺栓应力检测的实用性. 2014年，徐春广等[11]依据声弹性理论，采用纵横波相结合法，对栓体长度未知的紧固螺栓轴向应力进行测量，测量误差小于2.936 7%，大幅提高了纵横波相结合法的精度. 2018年，西南交通大学的贾雪等[12]通过对8.8级碳钢和12.9级合金钢2种不同材质螺栓的实际测试和数据处理,实现基于声弹性效应的螺栓轴向应力的标定测试,得到反映螺栓轴向应力和超声波声时差的线性函数关系,其重复准确度达2%～5%，线性关系高度显著. 2019年，赵春华等[13]提出了一种在线检测风电机组螺栓轴向应力的方法，完成了应力检测到实时预警的过程. 2020年，西南交通大学的刘家斌等[14]研制了一套自动标定螺栓轴向应力和渡越时间关系的测量系统，重复精度可以到达±2%.

本文基于声弹性效应原理，采用纵横波结合法，设计了螺栓拉伸标定实验，并建立了新的螺栓轴向应力计算模型，以期得到更加准确的螺栓轴向应力与超声波渡越时间的对应关系.

1 检测原理

根据声弹性效应，对于均匀弹性固体材料，若其为各向异性，并且纵横波传播方向与应力方向一致时，声速与应力的关系[15]为

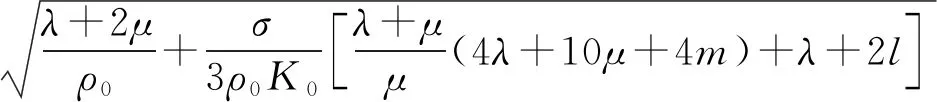
(1)

(2)

(3)

式(1)和(2)分别为在应力作用下，纵波、横波在螺栓内传播速度的变化规律.式中：VL和VT分别为螺栓在受应力状态下纵波、横波波速；λ、μ为拉梅常数；l、m、n为三阶弹性常数；K0是与材料拉梅常数有关的常数；ρ0为材料密度；σ为螺栓受到的应力.

材料的拉梅常数和三阶弹性常数与材料本身有关，故定义新的螺栓应力弹性系数

(4)

(5)

由于本文进行的实验研究都在室温下进行，故忽略温度对检测效果的影响.根据胡克定律，有

L0=L1+L2

(6)

(7)

(8)

(9)

式中：L0为螺栓未受力时的长度；L1和L2分别为螺栓受力区间和未受力区间的长度；Lσ为螺栓受力后，受力区间L1的长度变化；E为材料的杨氏模量；tL和tT分别为纵波、横波在螺栓内传播一个往返的时间.由式(4)～(7)求得

(10)

(11)

式中VL0和VT0分别为螺栓在无应力状态下纵波、横波波速.将式(10)(11)代入式(1)(2)，两式相除，可得

(12)

令

(13)

变换可得

(14)

X是仅与纵横波传播时间相关的函数，而新定义的螺栓应力弹性系数NL、NT与螺栓材料有关，需要通过实验测量.式(13)变换可得

(15)

令

(16)

可得Y-X的函数关系为

Y=-NTX+NL

(17)

2 螺栓轴向应力测量模型建立

2.1 实验设置

首先需要测量前文中定义的螺栓应力弹性系数NL、NT.为了向螺栓施加准确的轴向应力，设计了螺栓拉伸实验.实验选用螺栓型号为M30×150的8.8级碳钢.螺栓的模型尺寸如图1所示.

图1 螺栓模型示意图

实验使用脉冲激励接收仪实现纵横波的激励接收，传感器选用中心频率为5 MHz的压电传感器，用耦合剂紧密连接.拉伸机向螺栓施加指定大小的轴向拉应力，利用示波器显示并存储相应的超声波信号波形.螺栓拉伸实验示意图如图2所示.

图2 拉伸机拉伸螺栓示意图

2.2 渡越时间获取

由于本文主要针对在役螺栓的应力检测问题，故本次实验设定的应力施加范围为70～235 MPa，应力步进值为6 MPa，获取不同轴向应力作用下螺栓的声波波形.图3为螺栓受到70 MPa轴向应力作用下，激励横波压电传感器所采集到的声波回波信号.

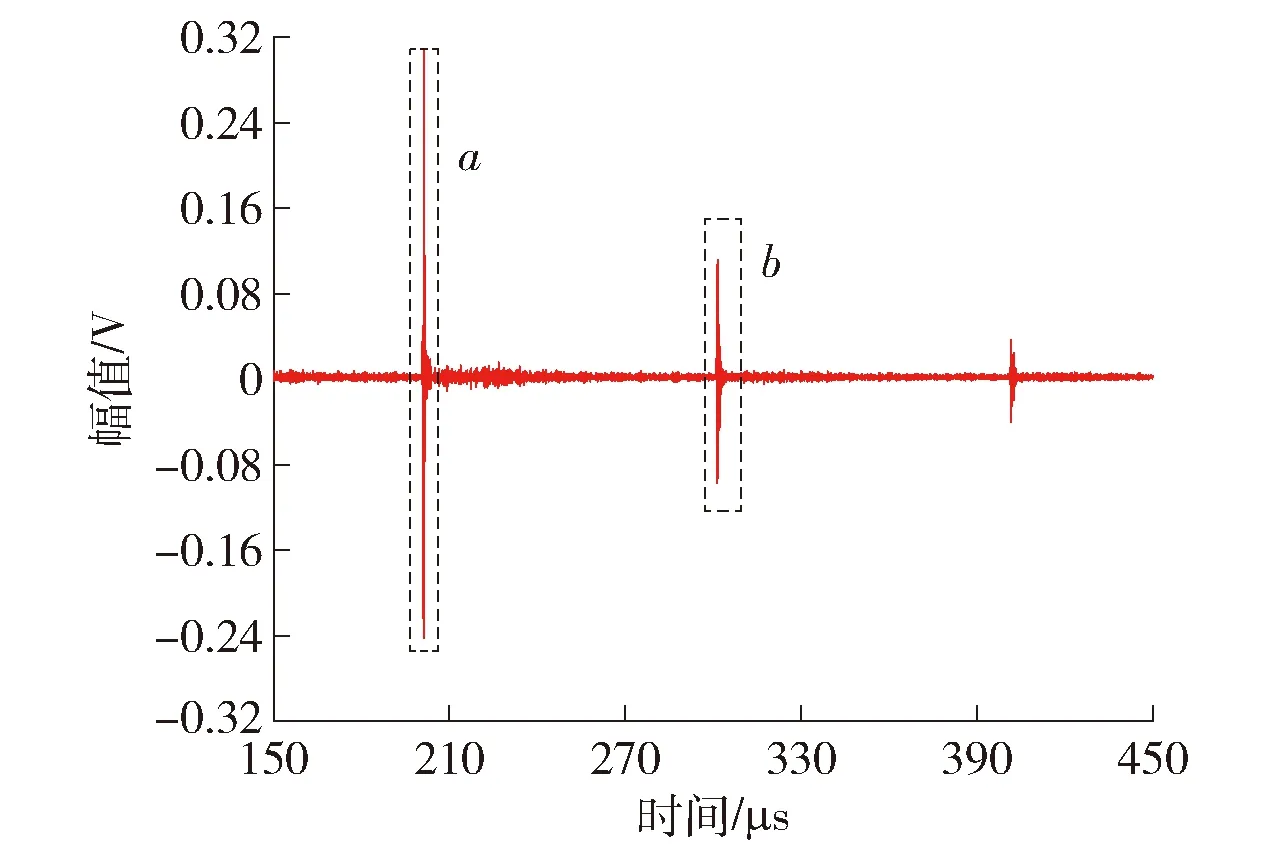
图3 横波回波信号

通过时间互相关法从回波信号中获取超声波的渡越时间.该方法能有效地利用回波信号的整体信息，降低突发噪声、白噪声和相位反转对获取结果的影响[17].

由图3可见，超声脉冲激励可产生多次回波信号，且每个回波信号频率和周期相同.设信号周期为T，信号之间的延时为τ，则2个回波信号的x(t)和y(t)的互相关函数Rxy(τ)可表示为

(18)

将各次回波信号进行互相关运算，得到互相关系数曲线，相关系数最大的位置所对应的时间就是两回波信号之间的延时τ，即为对应的超声波渡越时间.

以螺栓受到70 MPa轴向应力作用下，激励横波传感器所采集到的声波回波信号为例，对信号回波a和回波b做互相关运算，结果如图4所示.

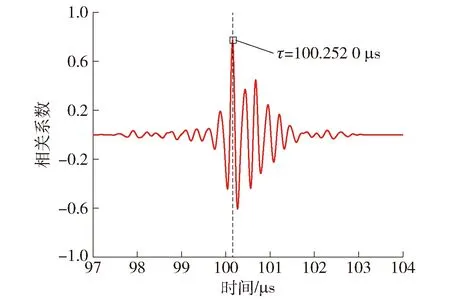
图4 横波相关系数曲线

根据图4互相关运算结果易知相关系数最大的位置为100.252 0 μs，也就是螺栓在该应力作用下的横波渡越时间.同理可求得不同应力作用下螺栓的横波渡越时间.

同样螺栓受到70 MPa轴向应力作用下，激励纵波压电传感器所采集到的超声波回波信号如图5所示.

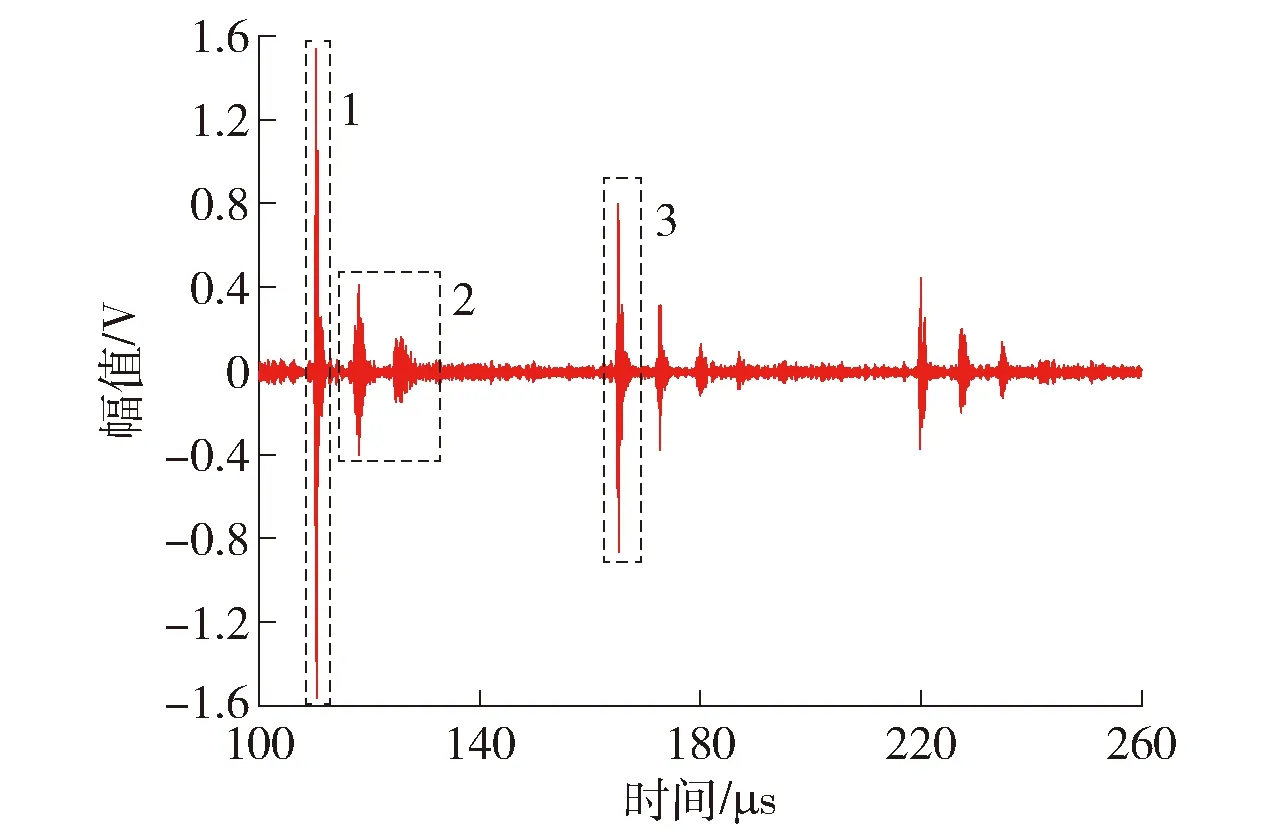
图5 纵波回波信号

图5中波形1和波形3为纵波在螺栓内传播，经螺栓底部反射回螺栓头部所采集到的回波信号.而纵波声源放置于端面检测细长工件时，扩散的纵波在被测工件的侧壁会发生波形转换，形成横波.该横波在被测工件的另一侧壁又会转换为纵波.由于横波的声速小于纵波，传播时间比直接从底面反射的纵波时间长，此类回波称之为迟到波[19]，如图5中的回波2所示.

对图5中的波形1和波形3做互相关运算，运算结果如图6所示.

图6 纵波相关系数曲线

根据图6互相关运算结果易知相关系数最大的位置为54.701 2 μs，此为螺栓在70 MPa应力作用下的纵波渡越时间.

通过批量互相关运算，求得不同轴向应力作用下纵横波的渡越时间如图7所示.利用互相关处理不仅提高了渡越时间的提取精度，还实现了回波信号的批量计算，提升了检测效率.

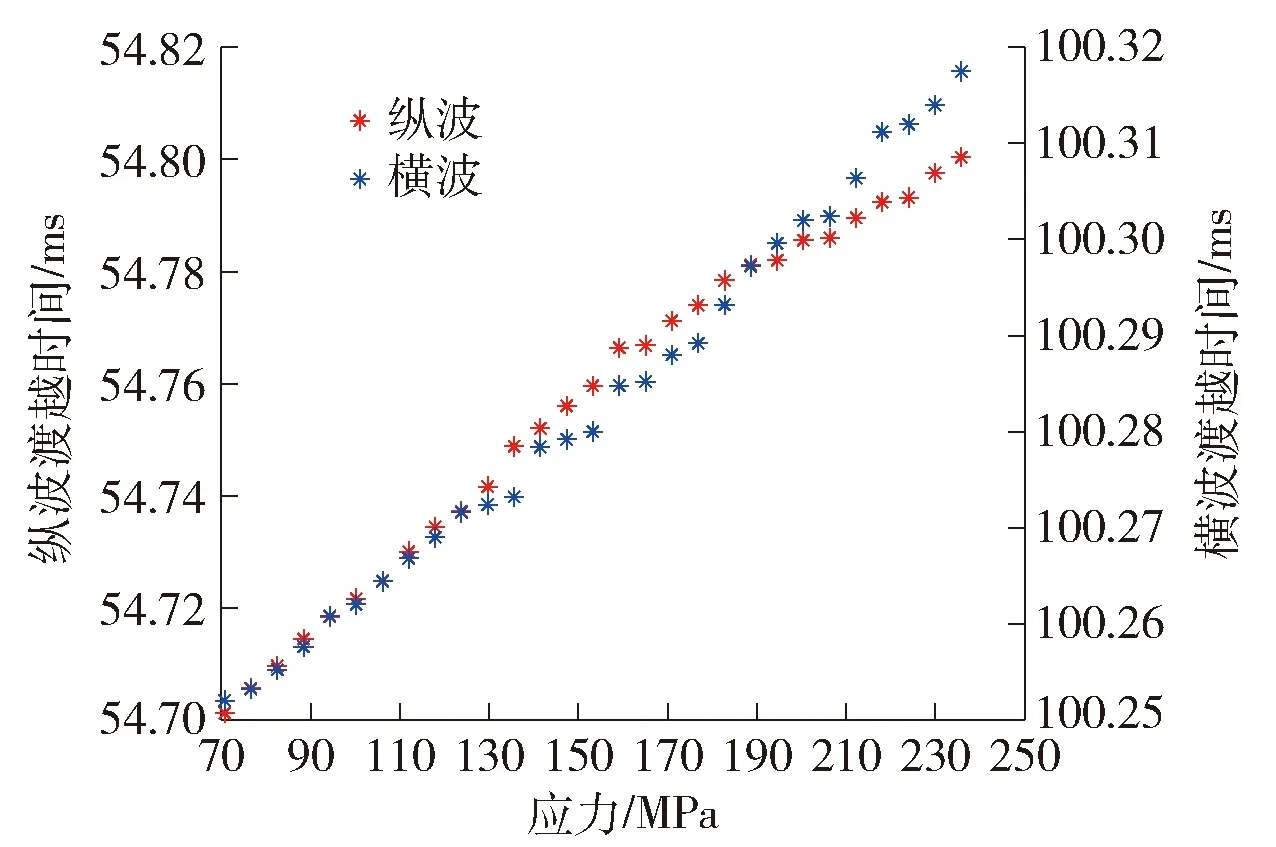
图7 纵横波渡越时间

2.3 模型拟合

将螺栓拉伸实验中获取的不同应力状态下的超声波渡越时间带入式(16)可得Y、X的关系曲线如图8所示.

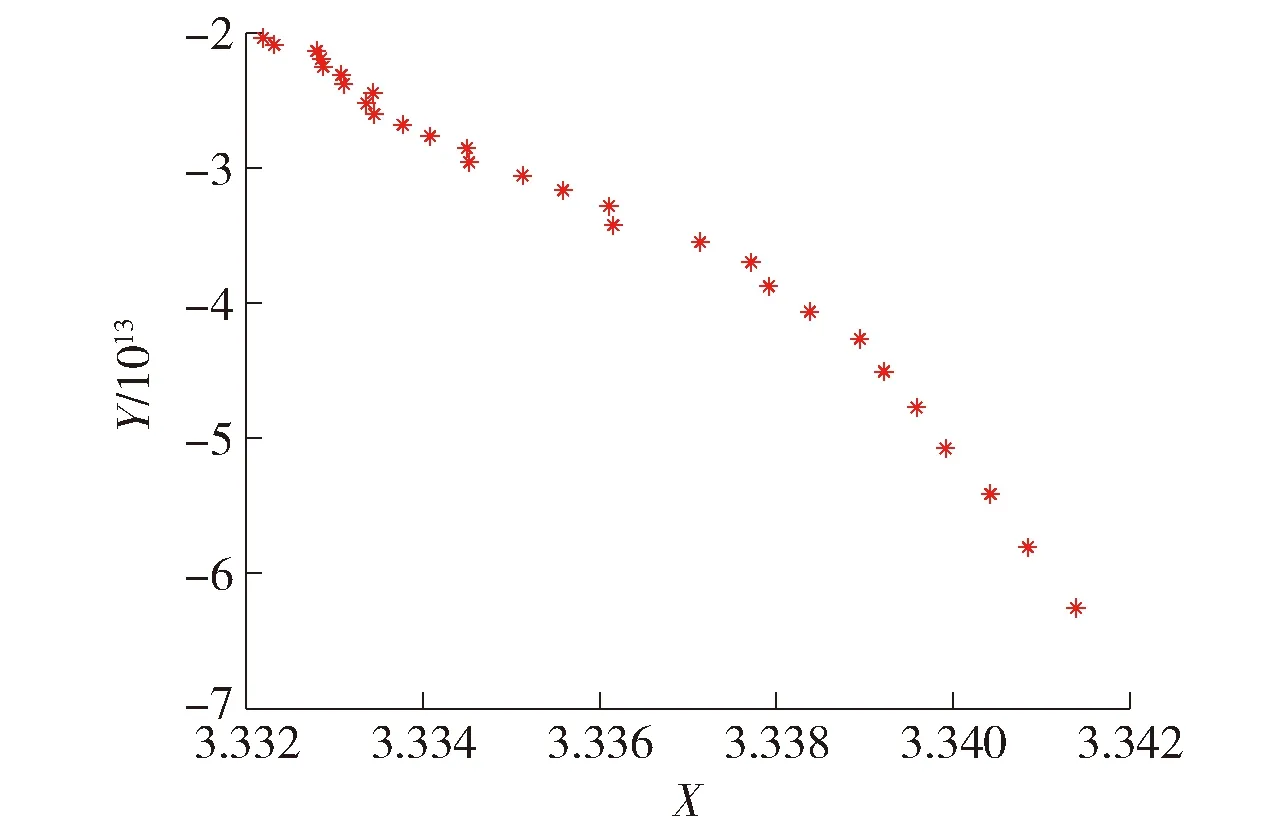
图8 Y-X关系曲线

若对Y-X曲线直接进行线性拟合，得表达式

Y=-3.966 9×1015X+1.319 9×1016

(19)

则根据表达式可得螺栓应力弹性系数NL=13.199 0×1015Pa，NT=3.966 9×1015Pa.结合式(14)并代入相应的渡越时间，可以初步获得螺栓轴向应力的计算值.

但观察图8曲线可见，Y和X并不是单纯的线性关系.这是由于螺栓在旋紧过程中，低应力条件下螺栓与螺母首先发生螺纹副的摩擦，随着夹紧力的不断增大，螺栓进入螺纹副的夹紧阶段.当螺栓受到的夹紧力达到临界值点后，才会完全进入弹性变形阶段[20].所以，螺栓的拉伸理论上会存在3个阶段.为探究实验所选螺栓进入各应力阶段的临界值点，对Y-X关系曲线进行高阶函数拟合，并求出该拟合函数的二阶导函数.二阶导函数取极值点处，即该点的斜率变化率最大，这也表示可在该点进行分段轴向应力计算.

首先，为了更加准确地拟合Y-X关系曲线，对原数据进行归一化处理.计算X的均值mu=3.335 9，标准差为sigma=0.002 937 8，定义新的变量

(20)

拟合出Y-Z的八次函数方程为

Y=-9.620 6×1011Z8+2.753 4×1012Z7+1.127 7×1012Z6-6.681 4×1012Z5+2.032 6×1011Z4+1.748 4×1012Z3-3.219 0×1011Z2-7.725 0×1012Z-3.259 3×1013

(21)

求拟合出的Y-Z八次函数方程的二阶导函数，并绘制图像如图9所示.

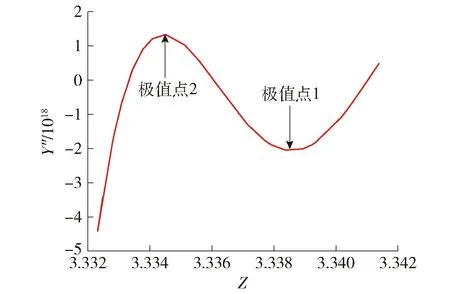
图9 Y-Z曲线二阶导函数

根据图9计算可得极值点1为110 MPa，极值点2为165 MPa.故应分别在110、165 MPa进行应力分段计算.各分段区间Y-X曲线如图10所示.

图10 分段模型曲线

分别拟合出70～110 、110～165和165～235 MPa三个阶段的螺栓应力弹性系数NL、NT.各分段区间的螺栓应力弹性系数NL、NT如表1所示.

表1 各分段区间螺栓应力弹性系数

2.4 检测结果对比分析

将求得的螺栓应力弹性系数代入到式(14)中，可得到该模型计算得到的相应应力值.通过不分段计算模型和分段计算模型分别求得的螺栓轴向应力值结果如表2所示.其中，理论应力值为拉伸机向螺栓施加的应力大小.

表2 螺栓轴向应力计算值结果

最后对计算模型的误差进行评估.若对Y-X曲线直接进行线性拟合，得到的计算应力值与理论应力值的平均误差为4.445%.而通过分段计算模型得到的计算应力值与理论应力值的平均误差可达2.026%，此方法极大地提高了螺栓轴向应力的测量精度.

根据表2的应力计算结果，绘制应力大小分布图如图11所示.

图11 计算应力值与理论应力值对比

3 结论

1) 基于声弹性效应原理，从理论上研究了不同应力状态下，纵横波渡越时间的变化规律；并通过定义新的螺栓应力弹性系数，初步建立了新的螺栓应力测量模型.

2) 设计了螺栓拉伸实验，获取螺栓在不同应力状态下，纵横波的回波信号；通过互相关算法批量计算螺栓的纵横波渡越时间，保证了渡越时间获取精度.实验结果分析表明：螺栓轴向应力与纵横波渡越时间呈线性关系.

3) 将实验获取的纵横波渡越时间代入到前文初步建立的螺栓应力测量模型.通过拟合高阶函数并求其二阶导函数，找到曲线的极值点进行分段计算.计算结果分析表明：应在110、165 MPa分段拟合螺栓应力弹性系数NL、NT；与理论应力值进行对比，误差率仅为2.026%.