半对称2SPU-2RPC并联机器人机构设计与运动学分析

卢月红，徐彩莲

(1.厦门华厦学院信息与智能机电学院，福建厦门 363100；2.厦门工学院机械与制造工程学院， 福建厦门 363100)

0 前言

三维平动和一维转动(3T1R)并联机构在水平方向上具有较好的顺应性，在竖直方向具有良好的刚性，广泛应用于分拣、包装、搬运以及装配等工业领域。3T1R按照动平台转动轴线可分为3种：3T1Rx、3T1Ry、3T1Rz。由平行四边形支链构成的3T1R并联机构(H4、I4、Par4和Heli4等)具有运动灵活、刚度大、加速度大的操作性能，即可实现三维移动和绕轴转动。近年来，越来越多的学者在3T1R机器人方面进行了很多创新性工作。文献[5]提出一种3T1R的四自由度并联机构，根据拓扑结构设计原理分析自由度特性，同时建立运动学方程，推导得到正逆解；利用数值法分析工作空间形状和大小，基于雅克比矩阵分析奇异位形以规避内部正解奇异。文献[6]设计了一种结构简单、构型对称、工作空间大的3T1R 并联机器人机构，根据螺旋理论验证其运动特性；建立运动学正逆解数学模型，分别分析机构的奇异性和操作空间等特性，给出了几种典型的奇异构型；最后，研究了可达工作空间的形状和几何约束条件之间的关系。文献[7]利用螺旋理论和约束螺旋综合法对3T1R完全解耦并联机构进行构型综合，根据螺旋理论构造所期望的正逆雅克比矩阵，通过支链驱动副布置得到支链的所有可能构型；综合得到一类由支链上独立输入驱动的完全解耦并联机构。文献[8]根据并联机构拓扑结构设计理论设计一种单自由度输入的新型三平移一转动输出(3T1R)的并联机构，通过方位特征集分析机构的运动特性，建立运动学方程模型，同时通过数值解进行互验；利用仿真软件得到输出速度及加速度变化规律曲线；通过ADAMS软件进行运动仿真，得出位置点的运动轨迹。文献[9]设计一种完全对称的4RPUR并联机构，根据螺旋理论推导出机构的自由度和运动性质；通过杆长约束条件建立数学模型，分析运动学正逆解；采用差分进化算法解决无约束优化问题(位置正解计算问题)，并提出一种新型的矢量变异策略简化算法以提高优化效率；最后，通过与其他算法对比，证明其高效性。

受文献[10]启发，提出一种可实现三维移动和绕轴转动的3T1Ry并联机器人机构。通过方位特征集计算机构的拓扑结构特性，验证机构具有三平移一转动的运行性能。根据几何约束条件建立运动学数学方程模型，同时选择一组数值验证正逆解有效性。基于此，分析操作空间和奇异性等运动特性，给出正解和逆解奇异的存在条件。另外，分析参数对工作空间体积的影响，建立数学优化模型，完成机构结构尺寸参数的最优化设计。

1 并联机构设计

1.1 机构模型描述

2SPU-2RPC并联机构结构简图如图1 所示。机构为半对称机构，其中支链可描述为

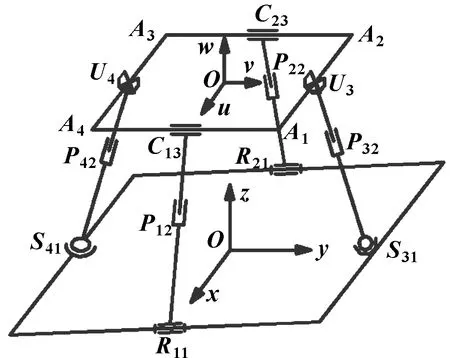
图1 机构的结构简图

1⊥2⊥3(1∥3)=1,2

1⊥2⊥()=3,4

该机构的支链1、2相同且对称分布，支链3、4相同且对称分布。动、静平台外切圆半径为、。根据并联机构分布特点，移动副作为驱动副，移动副的位移定义为(=1,2,3,4)，定义移动副的驱动范围为[,]。

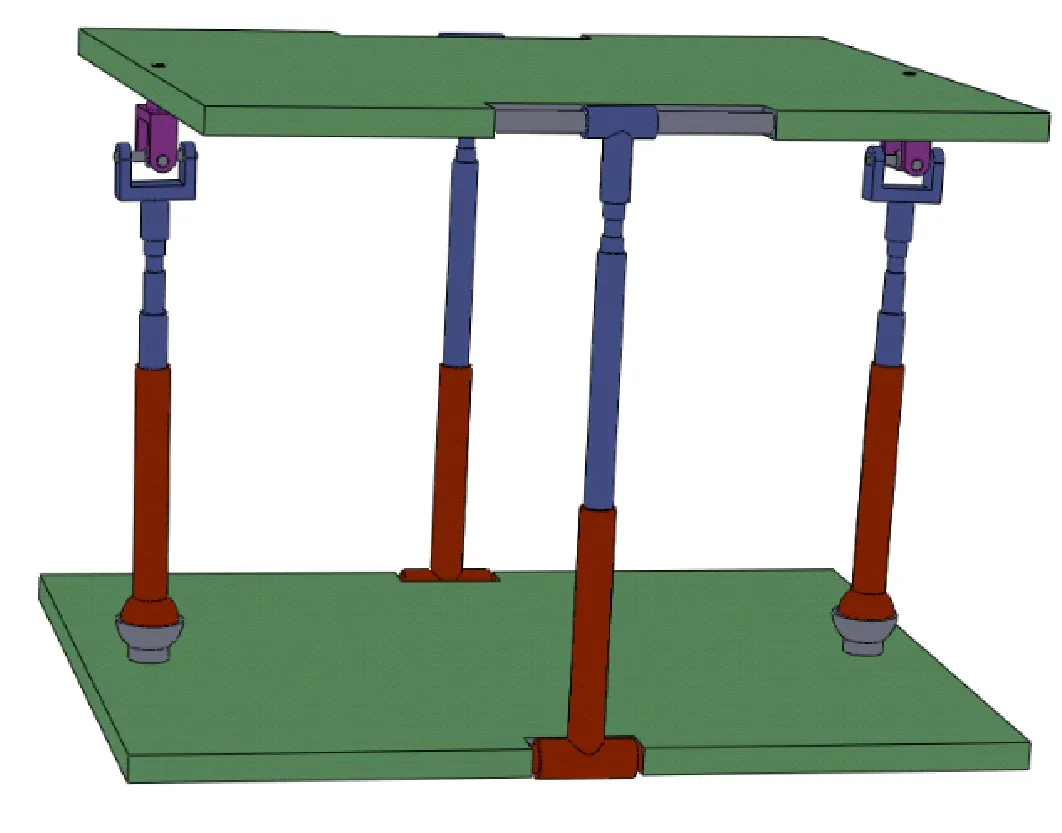
图2 2SPU-2RPC并联机构三维模型

1.2 机构的方位特征集分析

根据并联机构的拓扑结构计算支链末端构件的方位特征集，经计算4条支路构件的方位特征集为

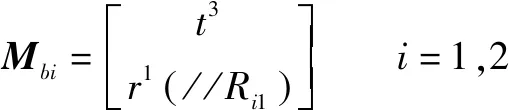
(1)

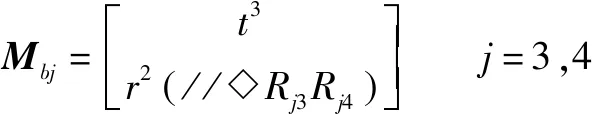
(2)

(1-2-3-4)=1∩2∩3∩4=

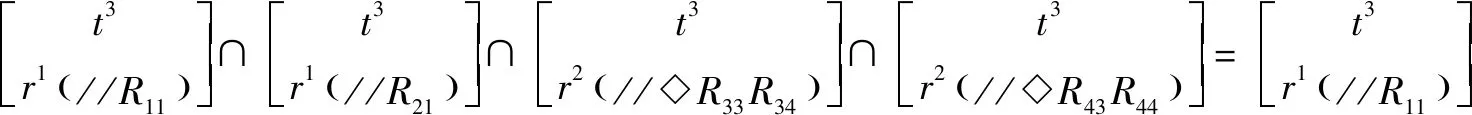
(3)

1.3 机构的自由度计算

自由度的计算公式有很多种，根据方位特征集的方法计算自由度，如公式所述:

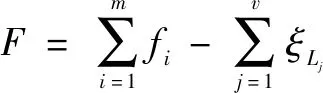
(4)

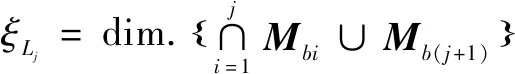
(5)

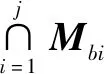
根据公式(4)、(5)计算得到自由度：

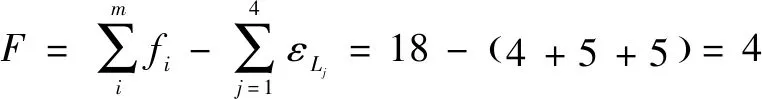
(6)

综上分析,机构的自由度为4，该机构可实现三维移动且绕轴转动的运动。

2 位置分析

2.1 位置逆解分析

机构的主动副是和静平台相连的移动副，动平台执行末端的位姿(,,,)，位置逆解可描述为根据位姿推导得到移动副的位移方程。在静、动平台的中心建立静坐标系{-}、动坐标系{-}， 具体分析过程如下：

根据参数定义得到静平台上转动副1坐标分别为(,0,0)、(-,0,0)、(0,-,0)、(0,,0)，机构动平台上的点与点在动坐标系{-}中表示为

(7)

为动平台绕定坐标系轴旋转角度，则旋转矩阵：

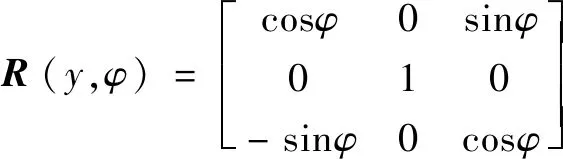
(8)

因此，根据坐标变换原理，可得点、在静坐标系下的坐标为

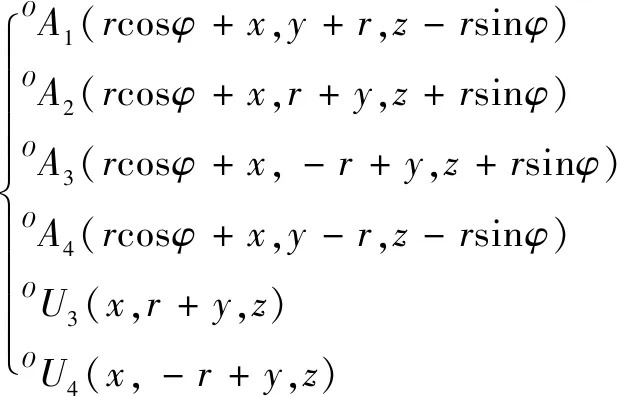
(9)

根据杆长约束条件可得如下等式：

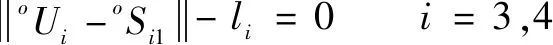
(10)

另外，在△和△中，运用向量之间的外积，可得到如下等式：

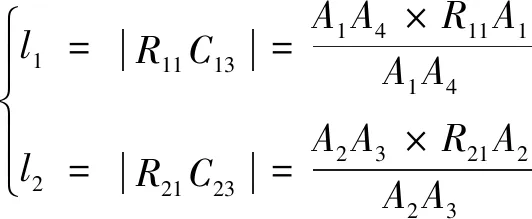
(11)

通过等式(10)(11)，将变量(=1,2,3,4)进行分离，推导可得运动学逆解(=1,2,3,4)表达式:

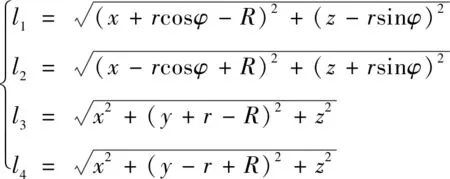
(12)

根据上述动平台的位置姿态，可由公式(12)得到位置逆解。

2.2 位置正解分析

位置正解是指根据输入求输出，即通过(=1,2,3,4)得到动平台末端的位姿(,,,)。根据等式(12)，分离变量得到有关于(,,,)的方程组:

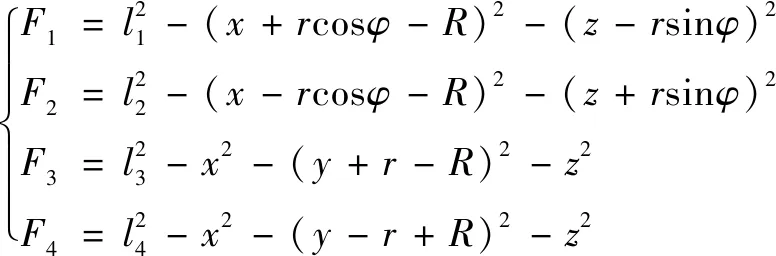
(13)

针对高次非线性方程组，可用Newton-Raphson方法进行计算。

2.3 位置正解逆解算例

根据公式(13)，解高次非线性方程组，可得4组正解数值解，如表1所示。其中,=1 m、=0.8 m。

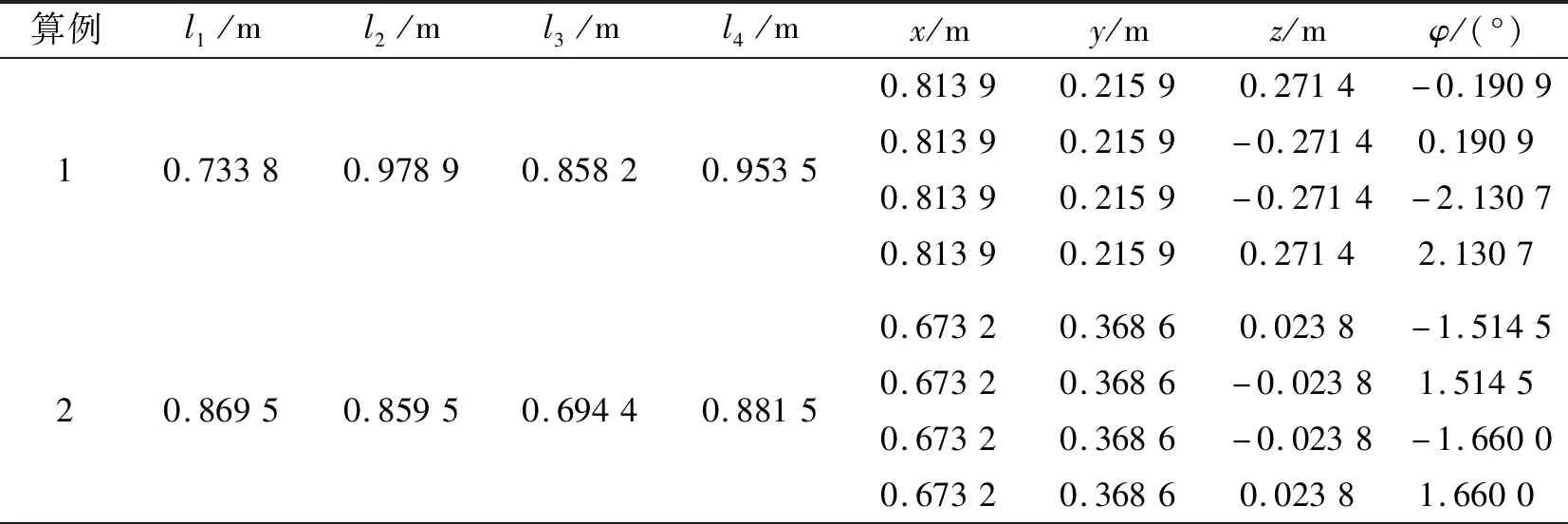
表1 部分正解算例

根据公式(12)，得到部分逆解算例，如表2所示。

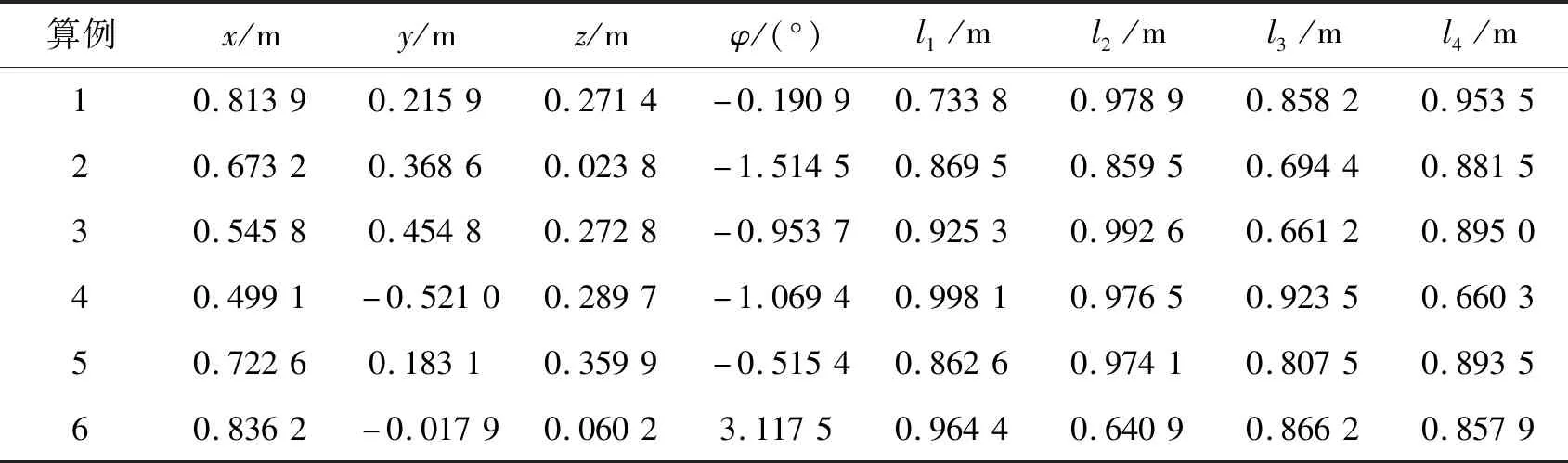
表2 部分逆解算例

由表1、表2可知：逆解的值能够完全匹配正解的值，验证了运动学正逆解计算的正确性。

3 奇异性分析

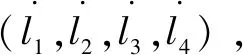
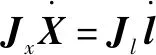
(14)

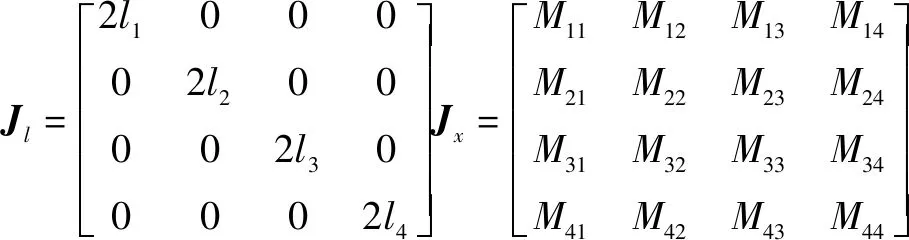
其中：为逆雅克比矩阵；为正雅克比矩阵。

若非奇异，则:

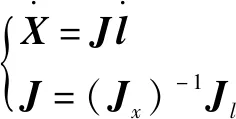
(15)

若非奇异，则:

(16)

其中:

=2(+cos-)

=2(-cos+)

===

=2(-sin)

=2(+sin)

=-2(sin-sin+cos)

=2(sin+sin+cos)

==2

=2(+-)，=2(-+)

==2

3.1 逆解奇异性分析

机构逆解奇异条件为det()=0且det()≠0，计算整理可得：det()=，则要求det()=0。

因此，存在以下情况，当任意支链的移动副驱动副位移为0，则存在逆解奇异。工程实际应用过程中可通过设置移动副的移动位移范围不包括极限位置，规避运动过程中存在逆解奇异的可能。

3.2 正解奇异性分析

机构正解奇异条件为det()=0且det()≠0，整理计算可得det()的表达式:

det()=16sin(-)(4cos-4-4sin)

令det()=0，因此，存在以下3种情况：

情况一：=0，即动平台的转角为0，调整位置姿态转动范围，可使得转动过程中避免这类情况出现；

情况二：=π/2且=()，控制参数的设置可以规避这类奇异出现;

情况三：=，机构选择过程中应使得动平台和静平台半径不同。

4 机构的工作空间分析

4.1 定姿态工作空间

表3所示为机构的一组尺寸参数，现在根据此参数进行定姿态工作空间的研究。

表3 机构的尺寸参数

图3所示为在表3参数下的定姿态的工作空间。可知:0°姿态角的工作空间最大，总体呈现圆柱包形状，底部是 “M”形掏空状态；30°姿态角下工作空间呈现“马桶”状，且工作空间体积逐渐减小；60°下工作空间更小，为不规则图形。90°～180°以上不存在工作空间，考虑对称性，360°与0°一致，不再赘述。

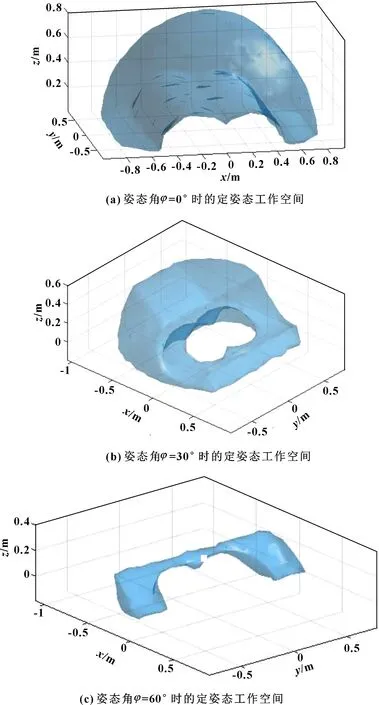
图3 不同姿态角下工作空间形状

为进一步研究姿态角对工作空间的影响，在不同姿态角下，对500个不同参数下工作空间体积的分布进行计算，结果如图4所示。

由图4可知：定姿态角工作空间体积大致按照180°呈对称分布，从0°到100°，工作空间体积分布越来越窄，最大值越来越小；在100°～250°姿态角内，工作空间体积都为0，即机构在较高的姿态角度内工作空间不存在。因此，此并联机构的应用设计应尽量选择低姿态角。

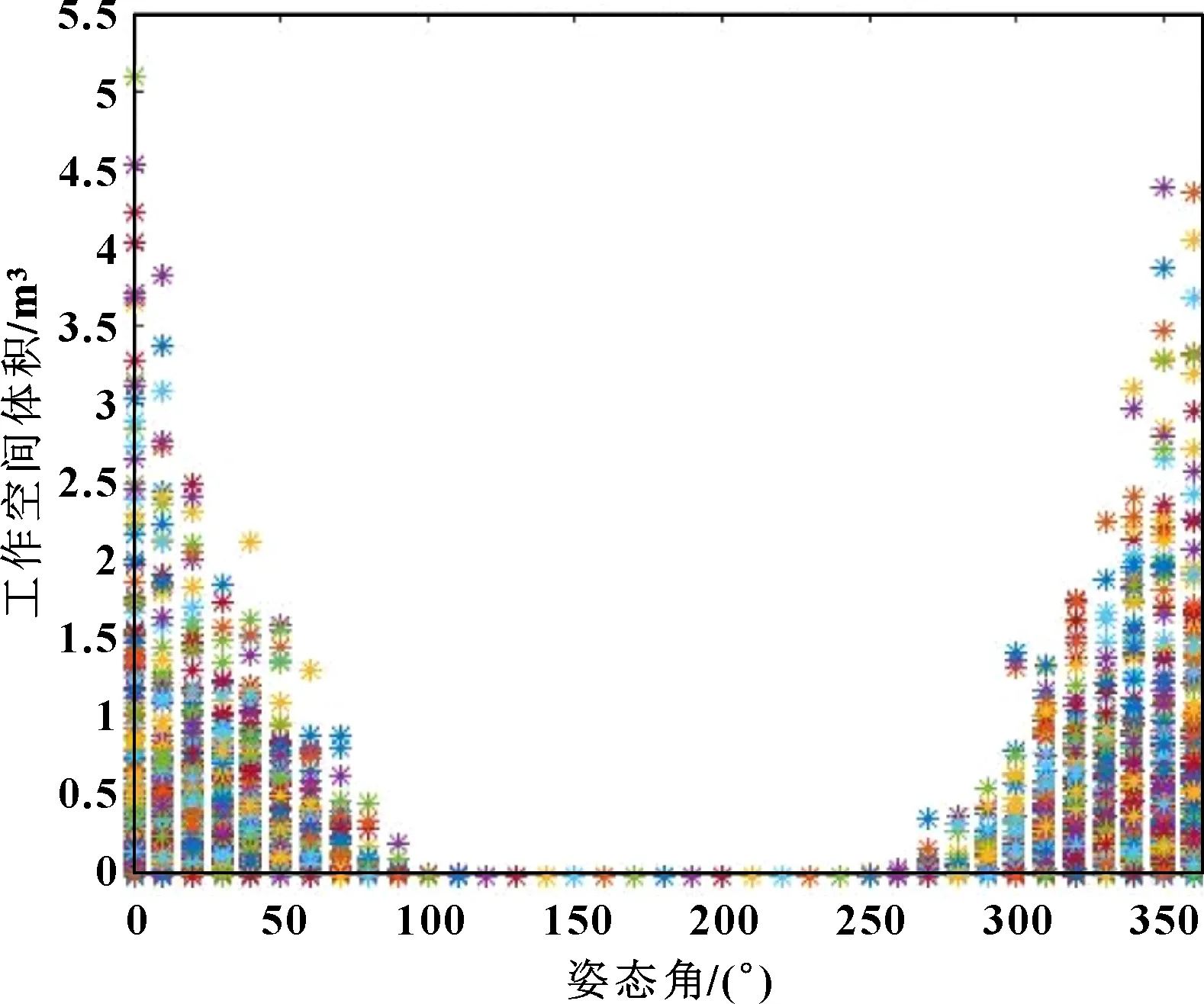
图4 姿态角对工作空间体积的影响

4.2 可达工作空间

根据表3的机构参数，计算得到该参数下的工作空间三维形状，如图5所示。该参数下，可达工作空间呈现“窝窝头”形状，内部有“M”形拱门空洞，工作空间连续光滑，体积较大，约为0.97 m。

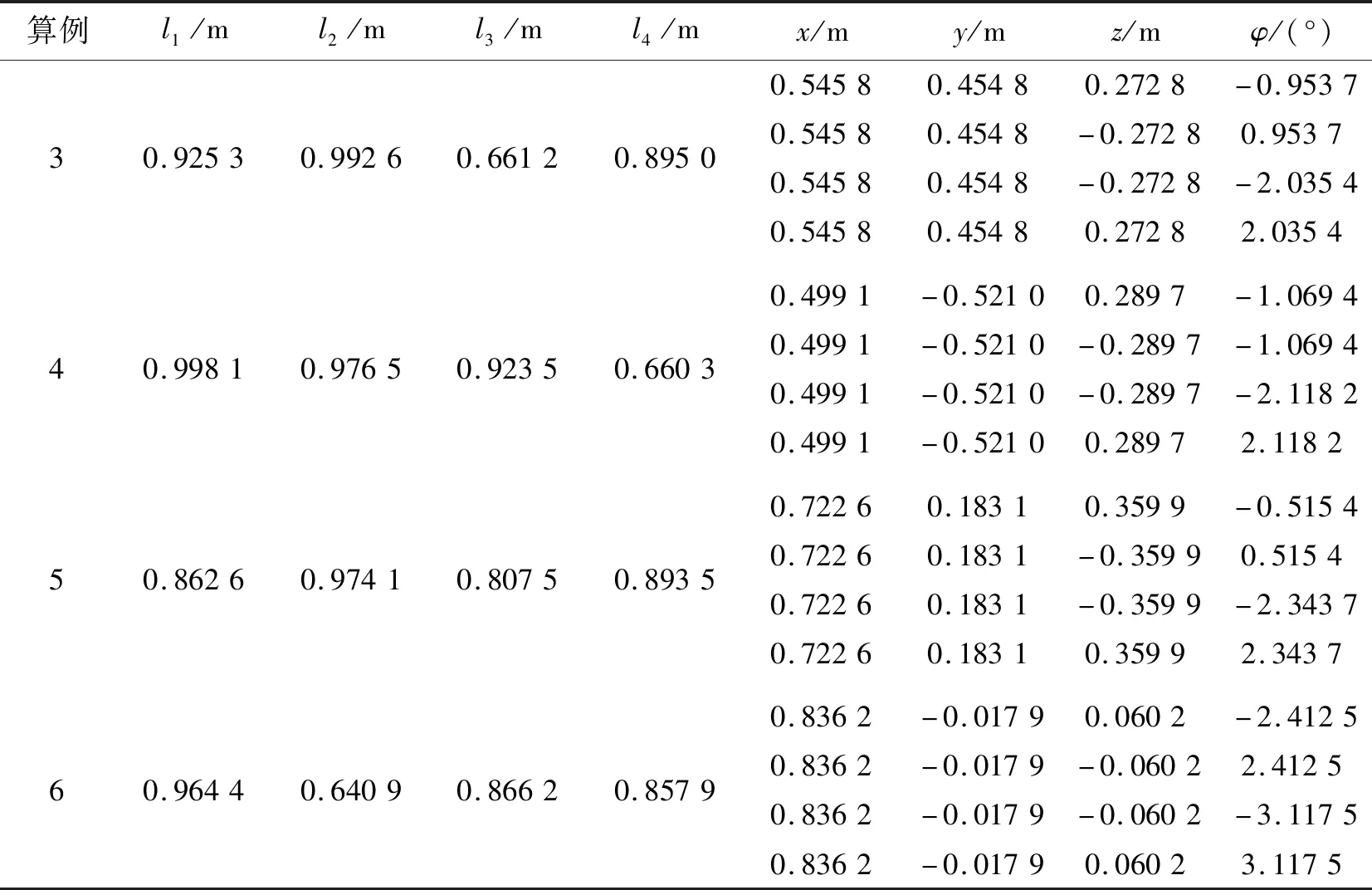
续 表1

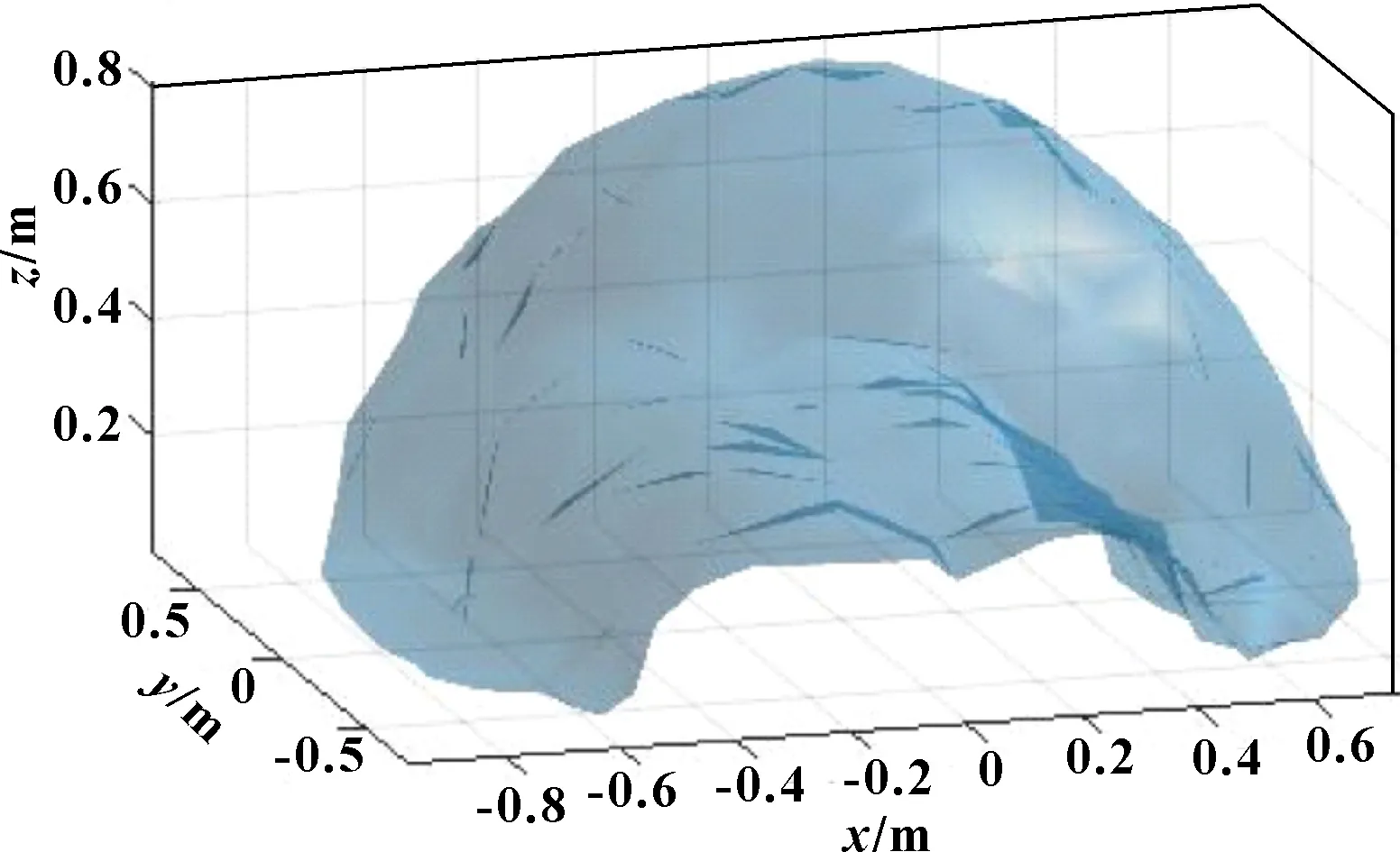
图5 机构可达工作空间(按表3参数)

5 参数对工作空间的影响

研究机构参数对可达工作空间体积的影响对并联机构的应用设计具有重要意义。为便于分析，选择单一变量法研究参数对可达工作空间的影响，即固定某一参数，其余参数变化，得到最大的可达工作空间体积，结果如图6所示。

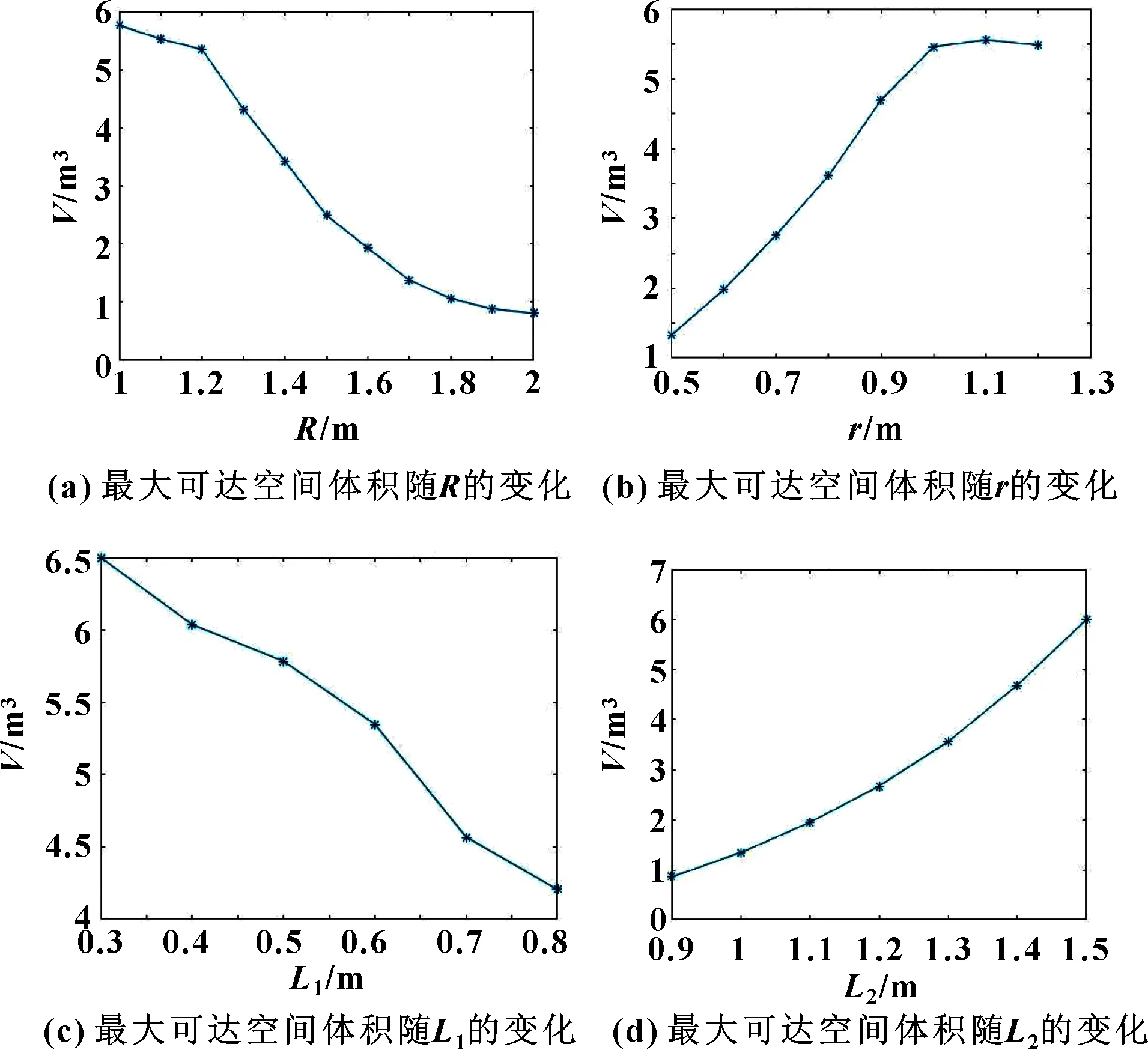
图6 结构参数对工作空间体积的影响

由图6可知：随的增大，可达工作空间逐渐减小，在=1 m时取得最大值；随的增大，可达工作空间逐步增大，在=1 m后，趋于稳定；随的增大,最大可达工作空间反而减小，但降幅较小，约2 m;随的增大，最大可达工作空间相应增加。从体积变化幅度看，的影响较小，其余参数影响较大，并且分析可得，最大可达工作空间的参数很可能在=1 m、=03 m、=15 m、≥09 m处产生。

6 工作空间的优化

6.1 优化模型的建立

在并联机构的设计过程中，期望机构的操作空间尽可能大。但考虑到并不是结构尺寸越大越好，建立并联机构工作空间最大化的数学优化模型，以得到一组最优参数解。

目标函数为：Max{(,,,)}

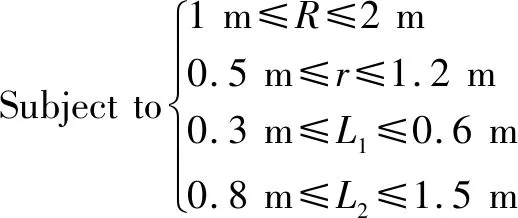
6.2 优化算法的选择

鲸鱼优化算法(Whale Optimization Algorithm，WOA)是一种元启发式优化算法，用随机个体或最优个体模拟座头鲸的捕猎行为，并用螺旋线模拟座头鲸的泡泡网攻击机制。

6.3 优化设计算例

选择如表4所示的鲸鱼优化参数，进行最大可达工作空间体积的优化，得到图7所示的优化过程。

表4 鲸鱼优化算法参数

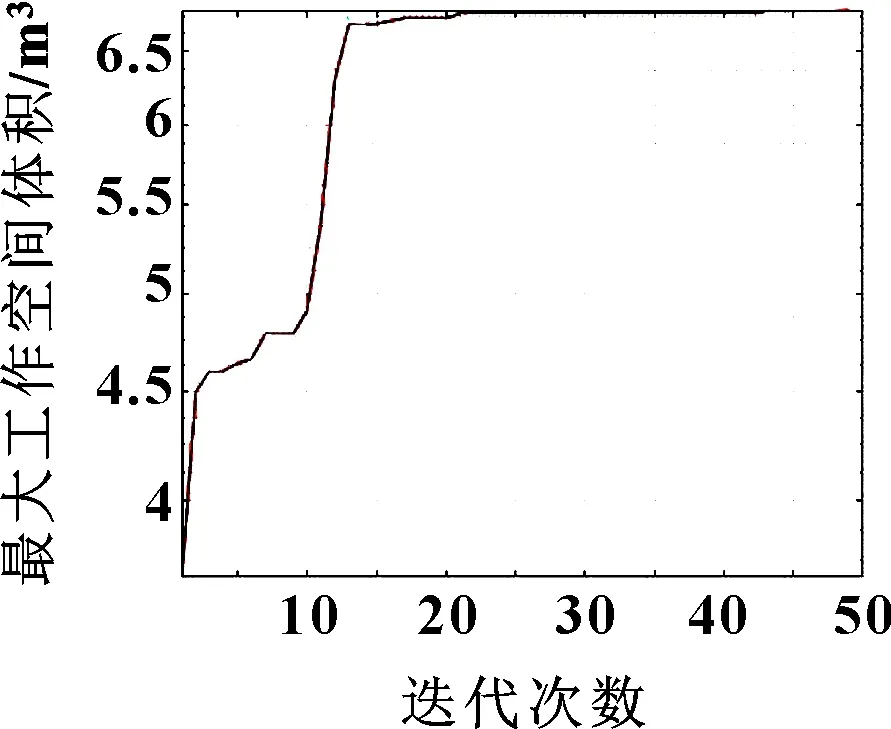
图7 鲸鱼算法最优化过程

由图7可知：迭代约23次时基本已收敛找到最大值。最大可达工作空间下的参数如表5所示。该参数基本和第5节的分析一致，≈1 m。图8所示为该参数下的可达工作空间的三维图，该可达工作空间体积较大，底部有一个半圆柱形小孔，体积约为6.67 m。

表5 WOA优化的机构参数

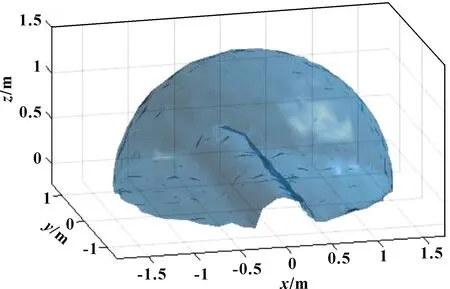
图8 最大可达工作空间的三维图

7 结论

(1)提出一种可实现三平移一转动的并联机构，利用方位特征集理论验证机构的运动性质。

(2)根据向量的外积和矢量法推导得到机构的运行学逆解方程，并根据Newton-Raphson方法计算机构的运动学正解方程的数值解。分别分析机构的奇异性和工作空间的运动学特性。运动过程中应避免运动到极限位置，以避免逆解奇异，同时应尽量避免姿态角等于0或=π2或=的情况出现，导致运动学正解奇异。

(3)分析了姿态角对工作空间体积的影响，结果表明：姿态角越大，工作空间的运动范围越小。因此，应尽量选择低姿态角下工作。

(4)分析了参数对工作空间的影响，结果表明：、越大，机构的操作空间越大；、参数值越大，机构的操作空间范围越小。