直升机救助模拟器支撑横梁随机振动响应分析
王盛业,王海涛,熊伟,关广丰
(大连海事大学船舶与海洋工程学院,辽宁大连 116026)
0 前言
直升机悬停救助模拟器用于在陆上实验室中模拟训练救生人员在恶劣海况条件下运用特殊救助装备(专用绞车、救援套、高绳等)进行直升机悬停救助。桥式起重机横梁作为直升机模拟器的重要承载结构件,六自由度运动平台和模拟机舱的支撑力全部来自起重机横梁。横梁跨度大,六自由度运动平台的模拟运动使横梁受到无规律的激振力,引起横梁振动,直接影响训练时机组人员的体感;同时,振幅过大会产生安全隐患。因此,需要对横梁进行振动响应分析,获取其振动特性,为今后解决柔性基座对运动平台的干扰问题提供研究基础。
目前起重机载重系统有两种建模方法:分布质量法和集中质量法。分布质量法多用于轻负载起吊过程的动力学分析。大负载起重机建模普遍采用集中质量法,该方法将负载视为一个质点,考虑负载摆动和起重机基础运动的耦合作用。CHIN等建立了起重机吊重系统的非线性模型,通过仿真获得了横梁最大响应的边界条件; MASOUD等建立吊重的空间摆球模型,分析了横梁基础运动和吊重运动的耦合作用;JU等将吊重简化为单摆系统,分析了固有频率对横梁动力学响应的影响。这些研究都以桥式起重机的起吊作业为应用背景,区别于一般起吊过程,直升机救助模拟器除了吊运救生人员,自身也通过六自由度平台进行模拟运动,对起重机横梁产生激励。六自由度平台作为主要激励源,动力学模型复杂,有必要将其用集中质量法进行简化。
随着CAE 软件的不断发展,采用先进计算机及配套软件对机械部件乃至整个机器人系统进行仿真计算已经日渐成熟。ANSYS可提供静力学分析、模态分析、瞬态分析、响应谱分析以及随机振动分析等多种分析模块,使用该软件对桥式起重机天车横梁进行分析的文献屡见不鲜,研究内容从早期利用ANSYS模态分析模块对横梁的结构进行强度分析和模态分析,到近些年利用ANSYS各个模块通用性强的特点,在模态分析基础上对横梁进行参数优化或结构的轻量化设计。刘文静等用瞬态动力学模块分析了不同加载时间对横梁结构的冲击影响以及不同工位时横梁的动态响应特性;肖正明等对以钢丝绳拉力为载荷的桥式起重机进行瞬时动力学分析,建立了起吊过程的冲击疲劳损伤演化模型,估算了桥架疲劳裂纹形成寿命;冯立霞等基于桥式起重机的模态分析结果对其桥架进行谐响应分析,获得了不同频率简谐载荷作用下桥架的频谱特性;刘德昆等对水电站大型桥式起重机桥架进行谐响应分析,获得了桥架结构发生共振的频率、共振幅值及主振方向。文献中利用ANSYS对桥式起重机天车横梁的动力学分析大多涉及瞬态分析和谐响应分析,而对天车横梁在受到连续无规律载荷状态下的随机振动响应分析涉及较少。
为此,针对安装有直升机模拟器的桥式起重机横梁这种受连续激振的特殊应用场合,本文作者利用ANSYS模态分析模块以及随机振动响应模块建立了考虑直升机救助模拟器激振力的天车横梁的动力学模型,分析横梁的振动特性,并通过试验验证有限元仿真的可靠性。
1 柔性基座横梁振动特性分析
1.1 柔性基座的固有频率
直升机悬停救助模拟器的六自由度并联平台倒挂安装在桥式起重机上,平台底座与桥式起重机天车的小车联接,可随起重机的天车大范围移动;并联平台的动平台与直升机模拟机舱相连,如图1所示。

图1 直升机悬停救助模拟器组成
直升机悬停救助模拟器可简化为上方带有集中质量的简支梁,如图2所示。起重机横梁截面均匀,将简支梁视为均质等截面,考虑集中质量在横梁中点位置挠度最大,将集中质量块放置于简支梁中点,梁长度为,单位长度质量为,抗弯刚度为。

图2 起重机横梁简化为简支梁示意
简支梁在集中质量的作用下的静挠度曲线方程为
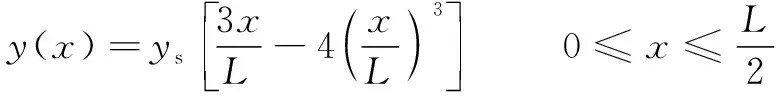
(1)
其中:为梁中点位置的静挠度,其值为
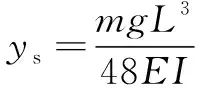
(2)
设梁中点的动挠度为,其运动规律遵循幅值为的简谐运动
=sin(+)
(3)
则梁各处的动挠度曲线可表示为
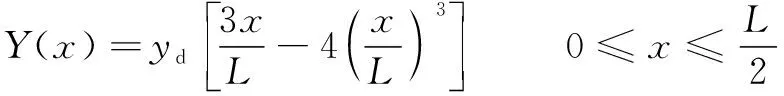
(4)
将梁划分为微段d,梁的总动能可表示为各微段动能之和,即
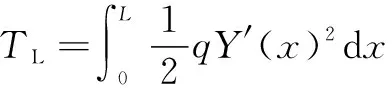
(5)
系统总动能为

(6)
系统总动能最大值为

(7)
系统的势能最大值为

(8)
其中:为梁的等效刚度系数,等效刚度系数值为
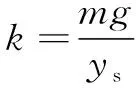
(9)
令系统的最大动能和最大势能相等=,可得固有频率为
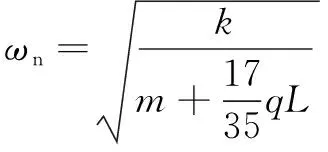
(10)
1.2 柔性基座模态分析
ANSYS模态分析是随机受迫振动响应分析的前置步骤,通过模态分析,可以了解结构的固有属性,得到结构的振动特性。
起重机横梁都由钢板焊接而成,由上盖板、下盖板和腹板围成箱体,钢板的厚度为30 mm,箱体内部支撑由加强筋、隔板、侧筋构成,如图3所示。

图3 起重机横梁箱体结构
横梁两侧腹板分别全程焊接两条厚度为10 mm的加强筋,隔板间隔1 500 mm,均匀安放在箱体内部。在上盖板和方钢轨道一侧腹板之间焊接侧筋板,板厚5 mm,间隔350 mm。在SolidWorks中建立横梁几何模型,将模型导入到ANSYS Workbench中。桥式起重机横梁箱体内部支撑情况如图 4所示。

图4 起重机主梁内部支撑结构透视图
横梁材料选取Q235B,其性能参数为密度为7.85×10kg/m,屈服强度为235 MPa,抗拉强度为400 MPa,弹性模量为206 GPa,泊松比为0.3。将横梁简化为上方带有集中质量的简支梁,考虑横梁极限挠度,将集中质量置于横梁中点处。在天车小车轮毂与横梁接触处设置细长加载面E、F,在E、F处分别添加集中质量,大小为3 000 kg,集中质量由小车、六自由度平台、模拟机舱以及配电设备等的质量构成,如图5所示。在主梁两端设置接触面A、B、C、D,接触面由螺栓连接将起重机主梁固定在端梁上,将接触面设置为固定约束。

图5 起重机主梁模型边界条件设置
对横梁进行模态分析,前6阶模态分析结果如表1所示。横梁1阶固有频率ANSYS求解结果为3.82 Hz,将横梁参数值代入公式(10)得到一阶固有频率为3.85 Hz,两者误差在0.1%以内,说明模态分析结果是可信的。一阶模态振动位移表现为前后摆动,是模拟器进行前后运动以及天车大车横梁运动时容易引起的振动形态;横梁二阶模态表现为上下摆动,是模拟器进行上下运动时容易引起的振动形态。横梁一阶和二阶模态相对最大变形产生在横梁的中点位置。
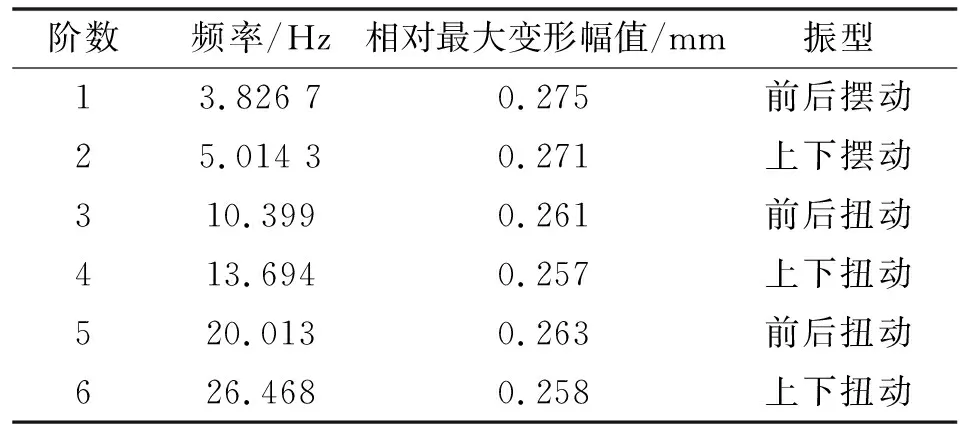
表1 横梁模态分析结果
实验室前期在交通运输部北海第一救助飞行队的直升机(型号为美国西科斯基公司S-76C)上采集了悬停飞行时的运动参数,记为模拟器运动数据1。通过分析发现,直升机动感模拟器运动时激振能量集中于4 Hz以下,主激振力方向为竖直向下。图6为直升机模拟器输入运动信号的功率谱,以1 W为基准功率,从功率谱可以看出信号能量在大于4 Hz以后呈指数递减,对横梁影响微小。

图6 模拟器输入信号能量谱
横梁的振动响应表现为各阶模态响应的叠加,由于一阶模态振动响应的振型为前后摆动,与主激振力方向不同,所以此研究中横梁主振型表现为二阶模态的上下摆动,频率为5.014 3 Hz,如图7所示。
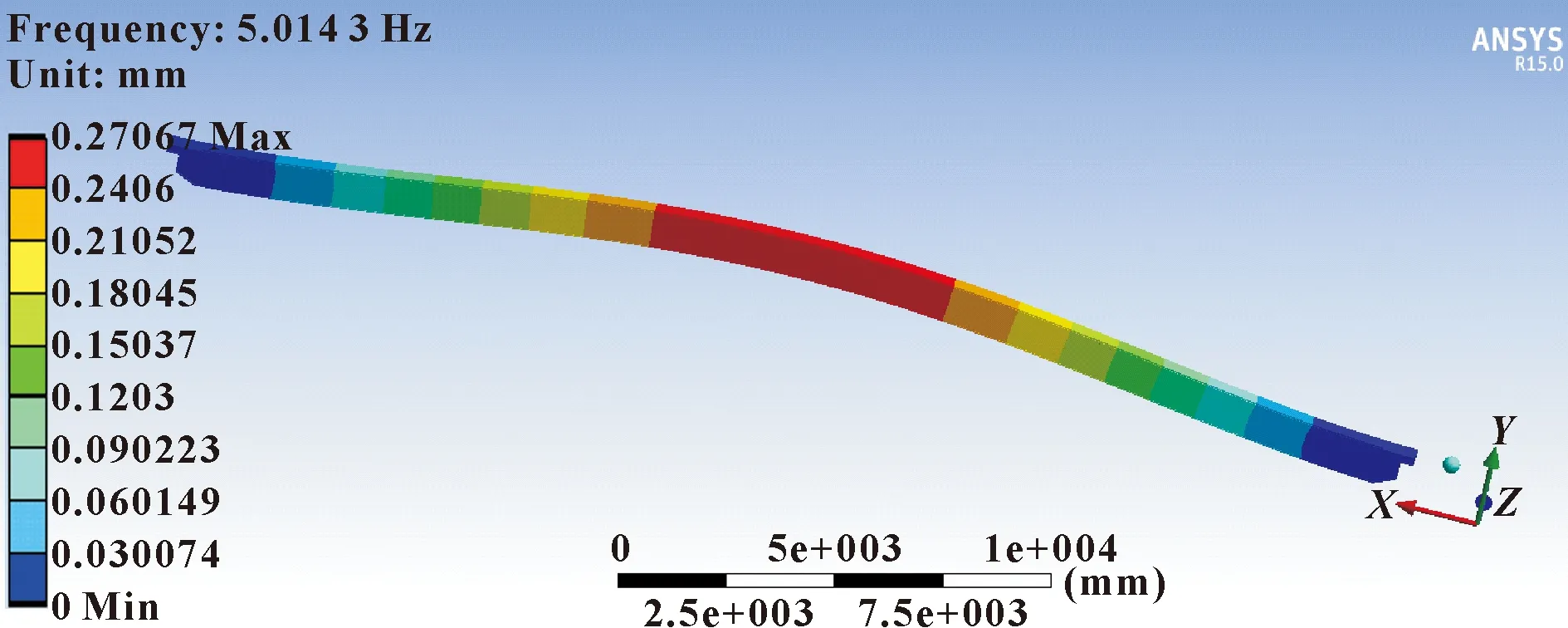
图7 起重机主梁二阶模态
2 随机受迫振动响应分析
2.1 激振力计算
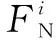

(=,,)
(11)
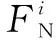
将公式(11)中支撑力模型转化为第1.1小节中放置集中质量为的横梁模型,简化后可得横梁的主激振力为式(12),方向竖直向下。

(12)
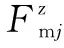
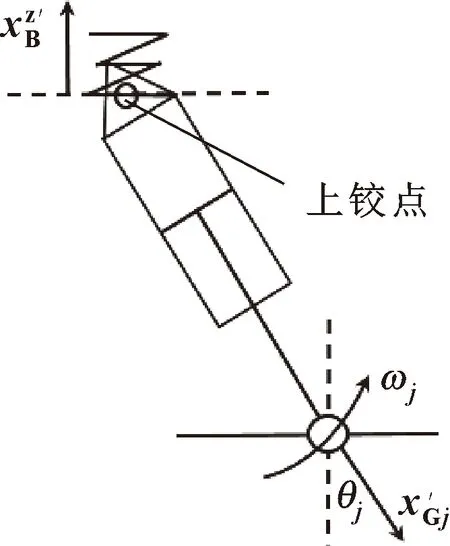
图8 支腿速度矢量图
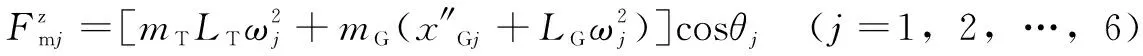
(13)
其中:为支腿缸筒的质量;为支腿缸杆的质量;为缸筒质心到上铰点距离;为缸杆质心到上铰点的距离;为支腿角速度;G为支腿缸杆伸出长度;为支腿轴线反向与垂向夹角。
六自由度并联平台结构参数如图9所示,分别包括静平台铰圆半径、动平台铰圆半径、静平台短边铰间距、动平台短边铰间距、中位缸长、电动缸行程等6个参数。由于六自由度平台的机构特点,根据以上6个参数就可以确定平台的基本结构。、分别为动、静平台的短边夹角。选取固定不动的静平台铰圆圆心为静坐标系的坐标原点,选取动铰圆圆心为动坐标系的坐标原点,定义平台中位为动平台初始位置。

图9 六自由度并联平台结构参数
将动平台6个铰点在坐标系中坐标用矩阵表示,铰支点在静坐标系中的坐标可用矩阵表示为
=·
(14)
转换矩阵可表示为下式
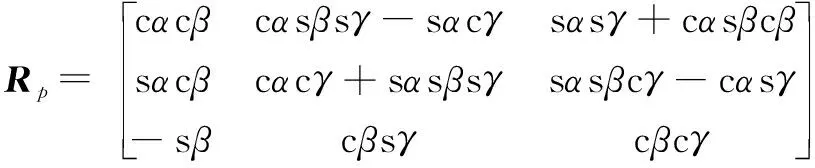
(15)
式中:c表示余弦符号cos; s表示正弦符号sin。
各支腿轴线方向的单位矢量可表示为
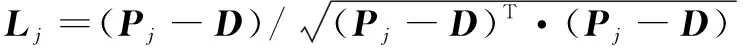
(=1,2,…,6)
(16)
其中:为静平台铰支点在静坐标系坐标。
各支腿沿轴线方向与竖直方向的夹角矩阵可表示为
=arccos(,)
(17)
各支腿伸长量矩阵表示为
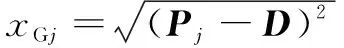
(18)
将公式(13) (17) (18)代入公式(12)计算,输入直升机悬停救助模拟器工作时六自由度并联平台的运动信号(模拟器运动数据1),信号包括并联平台平动和转动的运动参数,可以得到施加在天车横梁上的激振力曲线,如图10所示。

图10 施加在横梁的激振力
2.2 柔性基座动态响应
直升机悬停救助模拟系统工作时,六自由度并联平台带动模拟机舱运动,同时施加给起重机横梁随时间无规律变化的激振力。在这种非周期激振下,系统通常没有稳态,只有瞬态振动。无规律激励作用下系统响应的分析方法是把非周期激振力分解为一系列的脉冲载荷,系统响应则应由不同时刻脉冲载荷作用下的所有脉冲响应叠加而成。


(19)
其中:为物体的固有频率;为衰减振动频率;为阻尼系数。
当物体受到随时间变化的随机激振力时,激振力()可以看成一系列脉冲的叠加,对于线性系统,则可以用卷积形式来表示

(20)
将第1.2小节中主梁模态分析模块作为计算基础导入ANSYS随机振动响应模块,计算横梁受随机激振力时的位移响应。将天车小车与主梁接触面A、B作为加载面,输入用公式(12)求得的激振力曲线,设置界面如图11(a)所示。设置主梁阻尼为0.004,阻尼数值由时域衰减法测量获得,进行迭代计算。最终获得在此激振力下横梁的位移响应曲线,如图11(c)所示。可以看出:天车主梁振动曲线近似为周期为0.17 s、振幅为5 mm的简谐振动。由横梁振动特性分析可知:天车主梁将会按照以频率为5 Hz的二阶模态为主、其他模态为辅的复合形态进行振动,主梁的位移响应将是所有模态位移响应的叠加。由于集中质量的等效预应力(58 800 N)大于激振力(0~20 000 N),横梁的振动响应曲线幅值对激振力幅值变化表现出良好的跟随性,但变化并不剧烈,在无规律激振力的作用下,横梁竖直方向的振幅在2~7 mm之间变化。
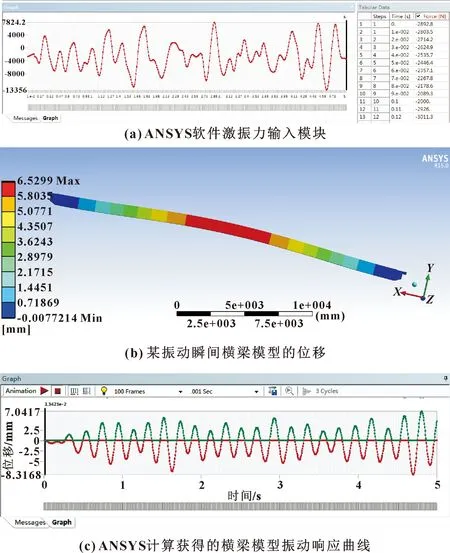
图11 ANSYS的柔性基座振动响应求解
2.3 振动响应试验验证与对比分析
对横梁振动响应进行测量,将型号为FT50220F(FT Technologies,精度0.2%MBE,分辨率小于0.1%MBE)的位移传感器安置于横梁/2处,向直升机模拟器输入运动信号(模拟器运动数据1),采集横梁在模拟器输入对应信号时产生运动引起横梁的振动响应曲线,对试验数据进行去噪处理后,与ANSYS计算曲线进行对比,如图12所示。可以看出:仿真曲线与试验曲线周期一致,误差在0.5%以内,仿真曲线幅值相比试验曲线幅值约有5%的偏差,有0.2 rad的相位偏差,误差受到滤波技术以及动力学建模精确程度的影响。整体上,仿真结果与试验曲线吻合良好,验证了该方法的可行性。

图12 横梁振动响应实验曲线与仿真曲线对比
3 结论
针对安装有无规律运动负载(六自由度平台)的桥式起重机天车横梁的受迫振动问题,应用ANSYS Workbench建立了天车横梁的有限元模型,通过模态分析以及随机振动响应分析,获取了天车横梁的随机振动特性。
(1)以直升机救助模拟器为对象建立细致的仿真模型难度较大,将系统简化为带有集中质量的简支梁,在ANSYS预应力模块对横梁进行模态分析,结果表明在六自由度并联平台的激励下,天车横梁会以固有频率为5.014 3 Hz二阶模态为主振型进行上下摆动。将横梁固有频率与数学建模的计算值进行比较,两者误差在1%以内。
(2)利用ANSYS随机响应模块进一步建立了考虑直升机救助模拟器动力学的天车横梁的ANSYS仿真模型,得到了在直升机模拟器运动激励下天车横梁的振动响应曲线,并与试验结果对比分析。结果显示:应用 ANSYS求解得到的振动响应曲线与试验测得的曲线吻合良好,通过试验对比验证了仿真结果的可靠性,为规避结构疲劳、共振等不良影响提供依据,为以后建立类似救助模拟器提供了参考。

