基于自适应滑模控制的刀盘伸缩系统研究

张杭军，方锦辉，杨宇柱，胡惠兵

(浙江大学流体动力与机电系统国家重点实验室，浙江杭州 310027)

0 前言

近年来，隧道掘进机广泛应用于隧道施工中，成为地下空间开发的利器。泥水平衡盾构能满足复杂地层、高水压、长距离工程建设需求，是目前穿江越河隧道工程的首选机型。同时，泥水盾构也面临着更多的挑战：刀具磨损更换问题，复杂地层盾构受困等。为了解决这些问题，中铁装备、铁建重工、浙江大学等单位研究设计了如图1所示的新型刀盘伸缩机构。刀盘固定在驱动箱上，并由驱动箱内多个电动或者液压马达驱动。驱动箱通过轴承连接到盾构主架。在驱动箱的背板上安装了多个呈圆形分布的伸缩缸，伸缩缸的另一侧连接支撑座。如果这些液压缸同步伸缩，则驱动箱将在轴承内环带动刀盘向前或向后移动，实现刀盘超挖，辅助换刀或者盾构脱困。另外，在驱动箱的两侧对称装有导向块，刀盘和驱动箱的反扭矩通过导向块传递到盾构主架，以提供反向支撑、伸缩导向并防止驱动箱在掘进过程中旋转。

图1 刀盘伸缩机构示意

盾构超挖的质量由刀盘实际运动轨迹和设计轨迹的偏差决定，而刀盘运动轨迹由伸缩缸实时控制。因此，精确控制伸缩缸是减少超挖误差和提高隧道施工安全性的重要技术。但电液系统存在很强的非线性，如阀口-非线性关系、随温度压力变化的油液特性等。电液系统也存在参数不确定性，如阻尼系数、时变负载等。这些特征增加了电液系统控制的难度。为了获得更好的动态特性，越来越多的研究人员研究非线性控制算法来补偿系统中的非线性和不确定性。在工作点附近使用极点配置将非线性系统局部线性化，但在全局范围内不能得到满意的控制效果。滑模控制被广泛应用于电液控制系统中，滑模面的动态行为不受参数不确定和外界干扰影响，但其控制输入的固有振颤会引发系统高频抖动。自适应控制的提出与应用有效地解决了模型不确定的影响，但其抗干扰能力较弱。 YAO和TOMIZUKA设计了一种自适应鲁棒控制，有效地集成了自适应控制和确定性鲁棒控制。YAO、LYU等将自适应鲁棒控制器应用于具有非线性和模型不确定性的液压执行器的轨迹跟踪，并取得了满意的结果。结合刀盘伸缩控制的难点，为提高刀盘伸缩机构在复杂地层中的精度和稳定性，提出一种将滑模控制和自适应鲁棒控制相结合的非线性控制，包括具有特殊自适应律的位置跟踪闭环，能补偿不确定的负载。通过李雅普诺夫函数验证闭环系统的稳定性，并通过AMESim和Simulink联合仿真进行模拟试验，验证该策略的有效性。

1 伸缩缸建模

刀盘伸缩系统并非实时工作，当需要更换刀具或者刀盘受困时适时启动，通过伸缩油缸带动刀盘前后运动实现超挖。单区伸缩缸的控制回路如图2所示，减压阀调定比例伺服阀的入口压力，比例伺服阀精确控制进出伸缩缸的流量和压力，平衡阀防止伸缩缸失速。伸缩缸的力平衡方程为

图2 伸缩缸液压示意

(1)

式中：和分别为伸缩缸无杆腔、有杆腔的压力；和分别为伸缩缸无杆腔、有杆腔的作用面积；为负载集中参数，包括刀盘负载、阻尼力、摩擦力等；为不确定的负载质量；为伸缩缸的位移。

伸缩缸的流量连续性方程为

(2)

式中：和分别为伸缩缸无杆腔、有杆腔初始体积；为工作油液有效弹性模量；为伸缩缸内泄漏系数，若采用零泄漏缸，可以忽略内泄漏；为从伺服比例阀流向伸缩缸无杆腔的流量；为从比例伺服阀流向伸缩缸有杆腔的流量。

比例伺服阀口的流量可以写成：

(3)

其中：

(4)

式中：1和2分别为比例伺服阀A、B口流量增益；为比例伺服阀的阀芯位移；为减压阀设定压力，即比例伺服阀P口压力；为比例伺服阀回油压力；为流量系数；和分别为比例伺服阀A、B口面积梯度；为工作油液密度。

由于伸缩缸系统的响应频率远远小于比例伺服阀的响应频率，可以忽略比例伺服阀的动态响应环节，将它视为比例过程：

=

(5)

式中：为电压位移增益；为控制输入电压。

将式(5)代入式(3)，得到新的阀口流量公式：

(6)

2 非线性控制器设计

定义系统状态变量为

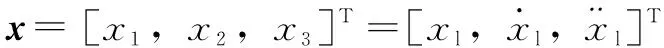
(7)

整合式(1)、(6)和(7)可以得到系统状态方程：

(8)

其中：

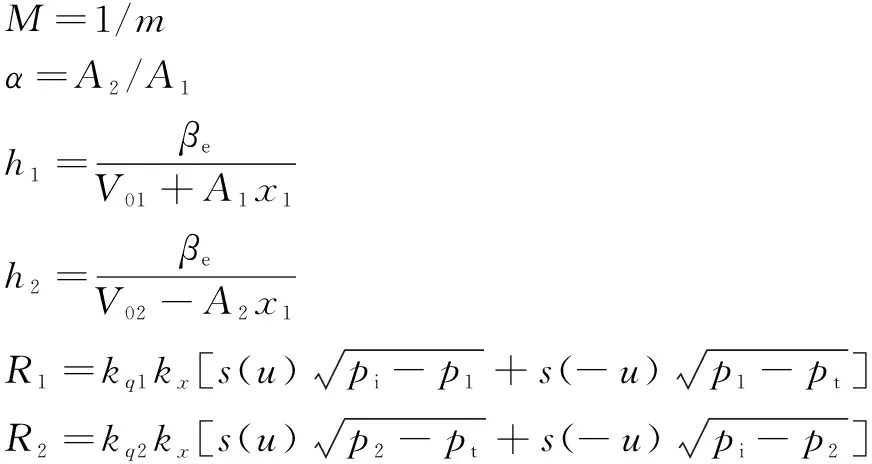
>>>0,>>>0

(9)

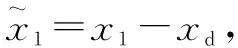
(10)

式中：为调节系数，为正常数。如果滑模面很小或者趋近于0，那么跟踪误差也会很小或者趋近于0。

对式(10)进行微分，得到其导数为

(11)

设计控制输入结构为

=+

(12)

式中：是为了满足轨迹跟踪而设计的可调节参数适应项；是鲁棒控制项。可以设为

(13)

将式(13)代入式(11)中，可以得到：

(14)

假设名义质量是有界的，且负载集中参数对应的加速度微分项也是有界的，则：

(15)

设计鲁棒控制项的结构为

=+

(16)

式中：为线性反馈项，用于系统稳定调节；为非线性鲁棒反馈项。可以设为

(17)

式中：为线性反馈系数，为正常数。

把式(17)代入式(14)中，可以将其化简为

(18)

设一个约束函数(,)：

(19)

可以设为

(20)

其中：

(21)

式中：为一个可以任意小的参数。

定义李雅普诺夫函数为

=12

(22)

对式(22)进行求导，并将式(18)代入，得：

(23)

名义质量的自适应率可以设为

(24)

其中：

(25)

式中：是一个正常数。

定义李雅普诺夫函数为

(26)

对式(26)进行微分，并将式(23)代入，得到：

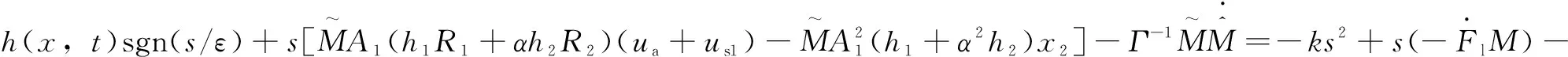
(27)

假设名义质量是一个未知的常数或者其变化率较低，那么的导数可以认为是0。

若滑模面满足||≥，则：

(28)

若滑模面满足||<, 则：

(29)

比例伺服阀的控制输入为

(30)

通过李雅普诺夫函数证实了包括非线性控制器和电液系统在内的整个闭环回路的稳定性。在有限的时间内，伸缩缸的跟踪误差趋近0。

3 仿真结果

为验证上述算法的有效性，进行AMESim和Simulink的联合仿真。图3为模拟试验台示意图，主要包括3支伸缩缸、3支负载缸和配套系统。每1支伸缩缸都由自身比例伺服控制回路控制；负载缸施加负载，模拟真实土层阻力。

图3 刀盘伸缩系统模拟试验台示意

图4 刀盘负载力

、、为伸缩缸在支撑座侧坐标点，、为伸缩缸在驱动箱侧坐标点，、、为刀盘负载作用点坐标，具体如式(31)所示：

(31)

式中：为驱动箱、支撑座的半径；为刀盘的半径；为到的距离；为到的距离。

非线性控制器参数和模拟系统参数如表1所示。

表1 控制器参数和模拟系统参数

3支伸缩缸的目标位移为

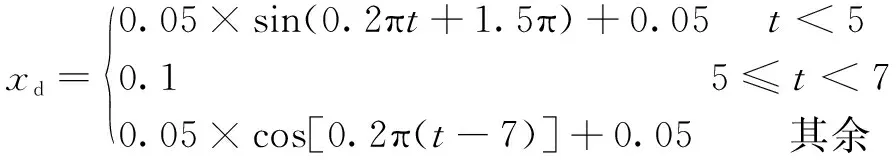
(32)

载质量的初始估计值为1 000 kg，作用在刀盘上的负载如图4所示。负载是不同频率的正弦力，作用在刀盘上致使刀盘抖动。设计伸缩缸同步伸出和缩回，目标轨迹如式(32)所示，非线性控制器合成比例伺服阀的输入电压，驱使伸缩缸跟随目标轨迹。图5所示为比例伺服阀的控制信号，输入电压是合理的，不存在高频振荡和长时间过饱和，这为后续伸缩缸平滑响应奠定了基础。图6所示为工作过程中伸缩缸两腔压力，压力符合假设约束在0～20 MPa。图7所示为滑模面参数。可知：值保持在±0.5内，位移、速度和加速度都能实现良好的跟随，且跟随误差较小。图8所示为质量估计的过程，在1 s内实现未知质量的近似估计。图9所示为3支伸缩缸的位移响应和跟踪误差。可知：在开始时，伸缩缸并没有实现跟随，主要由于控制系统的初始化参数和模拟系统参数存在较大差异，但在0.1 s内实现了调整，其后3支伸缩缸都得到了控制，实现了跟踪并保持误差在±0.1 mm内。运行过程中最大跟踪误差出现在缩回速度最大点；5～7 s内，伸缩油缸保持不动，稳态误差保持在±2 μm内。由此可知，全过程中每一支伸缩缸都得到了精确控制，刀盘按照设计实现扩挖。

图9 实际位移、目标位移与跟踪误差

AMESim和Simulink联合仿真证实了所提算法的有效性，它不单单能实现精确控制，完成跟随轨迹任务，也具有良好的自适应性。

4 结论

本文作者提出了基于自适应滑模控制的泥水盾构刀盘伸缩系统，滑模控制和自适应鲁棒控制相结合的非线性控制不仅可以补偿不确定的负载，而且具有很高的控制精度。通过李雅普诺夫理论验证了控制器的稳定性，并通过AMESim和Simulink联合仿真证明了其优异的性能。