极限挖掘载荷下挖掘机铲斗轻量化设计
孙浩然,任志贵,刘菊蓉,冯明豪,李佳豪
(陕西理工大学机械工程学院,陕西汉中 723000)
0 前言
挖掘机器人是传统挖掘机与互联网、自动化控制和人工智能等技术深度融合的产物,相比于传统挖掘机,挖掘机器人作业环境的适用范围更加广阔。在挖掘机器人轨迹规划中,常以能耗最优、时间最优、自主避障或轨迹光滑连续且振动冲击小为目标对挖掘轨迹进行优化,未考虑轨迹对机器人工作装置性能的影响。铲斗作为机器人任务执行终端与作业对象直接接触。复杂的作业对象产生了随机变化的挖掘阻力,对铲斗造成冲击与振动,使铲斗关键部位出现破损,学者们通常将由经验公式、不同工况得到的挖掘阻力、液压缸最大理论挖掘力或复合挖掘力作为载荷对铲斗进行强度分析。而铲斗结构优化中,许莉钧等以轻量化为目标,基于等强度理论对铲斗板厚进行了优化;殷淑芳、尹开勤以降低铲斗最大应力为目标,在极端工况下使用SolidWorks优化模块对铲斗进行了强度优化;沈振辉、杨拴强以铲斗最大应力不改变为约束条件,基于4种典型工况和Monte Carlo技术建立了挖掘机铲斗轻量化方法;邓子龙等以斗杆液压缸力臂最大为危险工况,以满足强度要求为前提对铲斗质量进行了优化;侯亚娟等以铲斗截面周长与面积的比值为目标函数建立了铲斗质量优化数学模型。以上研究仅在理想状态下,在某种工况下对铲斗的工作性能进行评价,未考虑挖掘轨迹对铲斗强度的影响及如何在保证强度的前提下对铲斗进行轻量化设计。
因此,本文作者提出一种基于极限挖掘力的铲斗轻量化设计方法。根据挖掘机器人实际挖掘过程选定了一条连续挖掘轨迹,对连续挖掘轨迹中液压缸的极限挖掘力进行计算,并将其作为外载荷对铲斗的结构强度进行分析,建立了铲斗结构优化模型,并使用枚举法对铲斗进行优化。
1 连续挖掘轨迹与极限挖掘力
实际挖掘过程中,与挖掘机器人工作性能发挥关联紧密的挖掘轨迹是由斗杆和铲斗的相对夹角共同决定,不同的夹角可使工作装置处于不同的位置,改变夹角便可得到不同的挖掘轨迹。地面以下是挖掘机器人的主要挖掘区域,在挖掘机器人设计之初便考虑主挖区对挖掘性能发挥的影响,因此,选择主挖区内的挖掘轨迹作为研究前提。基于连续挖掘轨迹理论,选择的连续挖掘轨迹如图1所示。
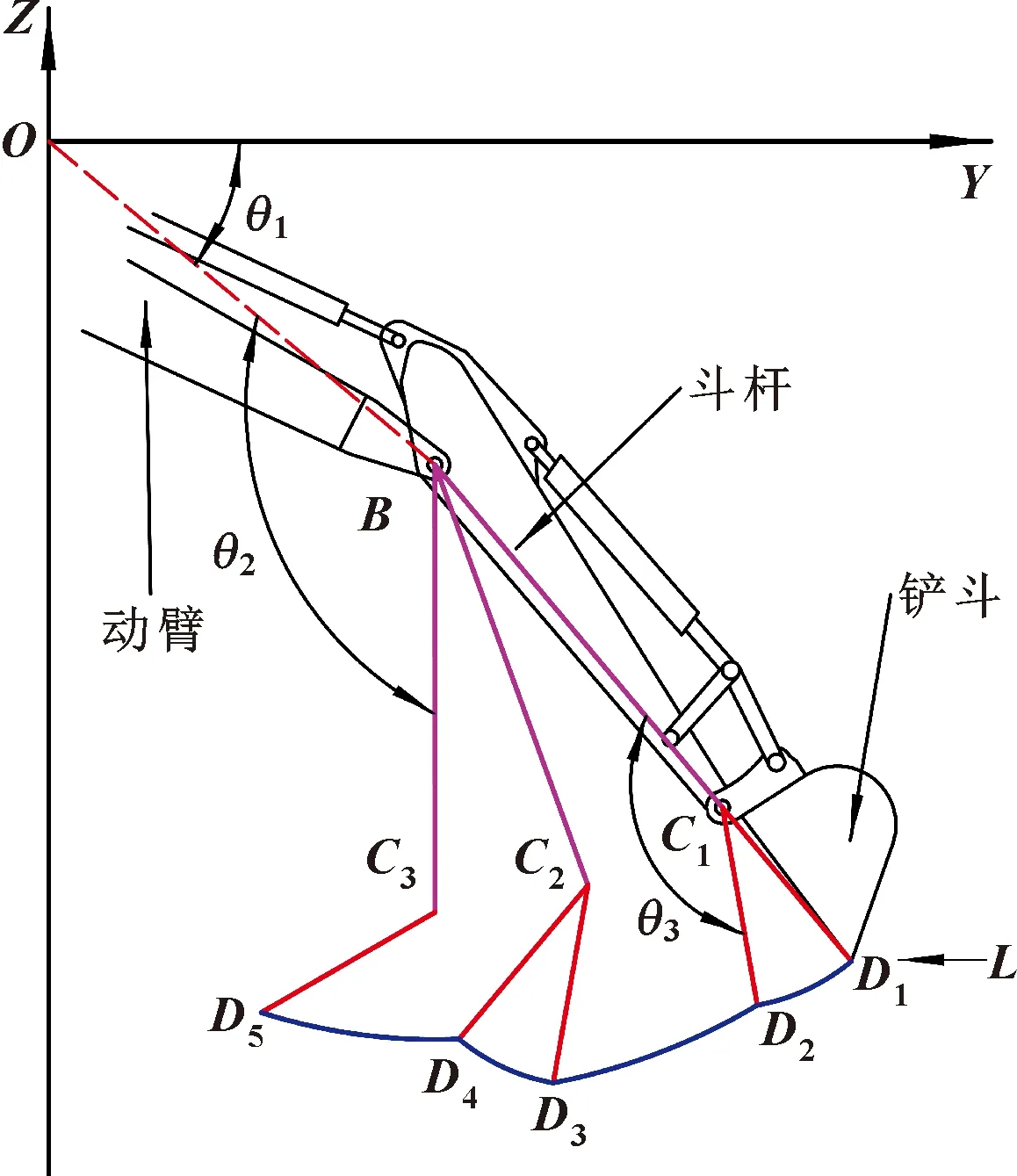
图1 连续挖掘轨迹
轨迹的起点为,终点为,动臂与轴夹角为-10°,此过程中交替使用铲斗液压缸、斗杆液压缸进行挖掘。轨迹由、、、等4段分轨迹组成。轨迹中机构夹角如表1所示,其中:角为动臂与水平面的相对夹角,角为斗杆与动臂的相对夹角,角为铲斗与斗杆的相对夹角。

表1 工作装置夹角 单位:(°)
学者们经常将理论挖掘力作为研究前提,但在测验中得到的挖掘力往往大于理论挖掘力模型的计算结果,理论挖掘力无法代表挖掘机器人所能发挥出的真实的挖掘力。由学者提出并已验证的极限挖掘力计算模型可知,实际挖掘过程中铲斗承受的是一个随时变化的复杂力系。
不考虑侧向力时,由于工作装置的对称性,该复杂力系可看作平面力系,将其合成为作用于铲斗切削刃中间位置点的切向力、法向力和阻力矩,合称为极限挖掘力,如图2所示,其中,阻力系数=/、阻力矩系数=/,其中:阻力系数取值范围为[-0.4,0.5],阻力矩系数取值范围为[-0.4,0.2]。
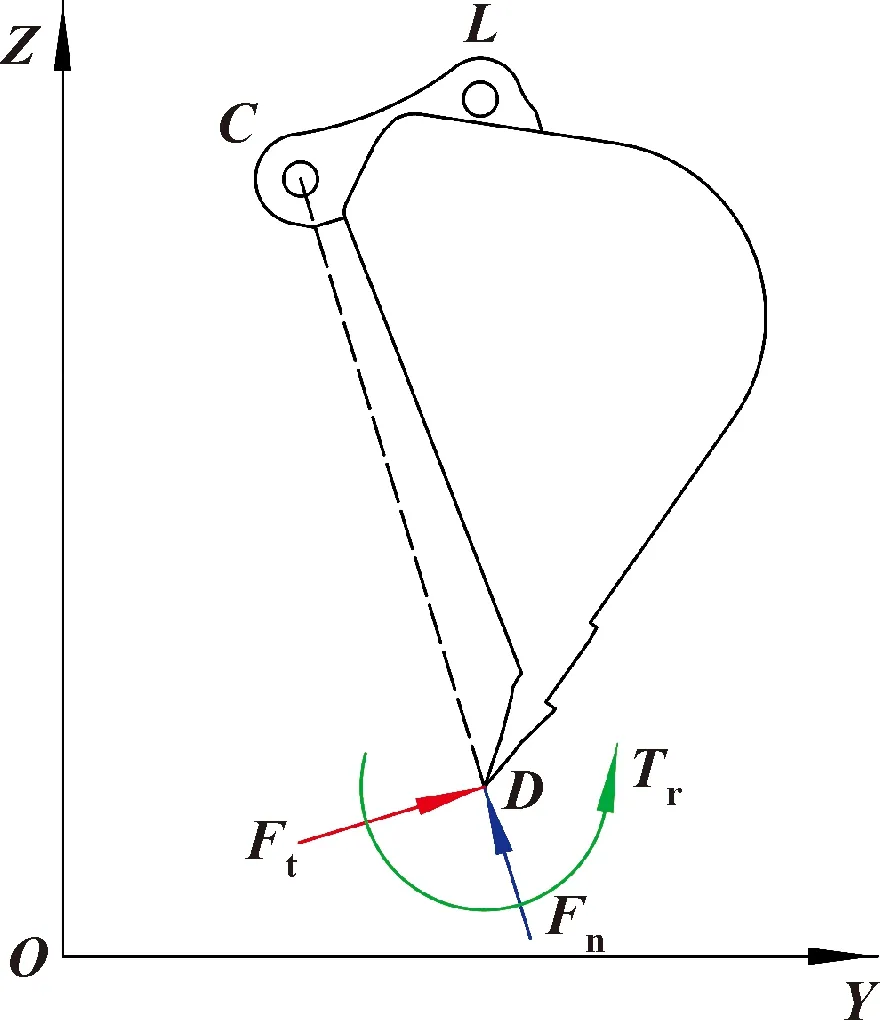
图2 极限挖掘力分布
不同的工装姿态对应不同的阻力系数和阻力矩系数,同时对应不同的切向力、法向力和阻力矩,并且极限挖掘力法向力和阻力矩是理论挖掘力模型所忽略的,因此,选择极限挖掘力作为铲斗外载荷较理论挖掘力更接近真实情况。铲斗、斗杆液压缸在4段轨迹中的极限挖掘力如图3所示。

图3 连续挖掘轨迹载荷
图3(a)中:随着减小,极限挖掘力的切向力、法向力和阻力矩曲线变化规律几乎完全一致,随着的减小而增大。图3(b)中:极限挖掘力的切向力、阻力矩曲线变化规律完全一致,随着的减小而增大;由于阻力系数的存在,极限挖掘力的法向力随着的变化出现上下波动状态。图3(c)中:轨迹中,极限挖掘力的法向力和阻力矩曲线变化规律完全一致,波峰波谷对应的数值一致,切向力变化规律与法向力、阻力矩相反。图3(d)中:轨迹中,极限挖掘力的切向力、法向力和阻力矩曲线变化规律几乎完全一致,随着的减小而减小,法向力偶尔出现波动。极限挖掘力最大切向力出现在挖掘点,此时,切向力=142.271 kN,法向力=-56.908 kN,阻力矩=-56.908 kN·m。
2 铲斗APDL建模与强度分析
由于反铲液压挖掘机铲斗的结构形状比较复杂,所以使用APDL语言对铲斗建模和有限元分析过程进行了参数化,并写入命令流文件。根据需求对命令流程序中的零件结构参数、材料参数、网格单元类型、载荷大小等参数进行赋值计算,将命令流文件保存,然后运行被赋值过的命令流文件。此过程实现了铲斗有限元分析计算的自动化。
在建立铲斗参数化模型过程中,在保留原铲斗主要结构、尺寸特征的前提下,为保证网格的顺利划分,建模之初就需忽略对有限元计算结果影响较小或者无影响的细节,如斗底加强板、耳板形状、斗齿的有无等。基于此原则做如下简化:(1)去除斗齿:将在铲斗斗前壁板上直接施加载荷;(2)简化耳板与背板:耳板、背板形状不规则,易增加建模时间;(3)删除侧切削刃:由于载荷直接作用于斗唇上,侧切削刃对铲斗结构强度影响较小,并且,此研究中的铲斗结构优化是铲斗基本形状的优化,不涉及侧切削刃,因此,在建模时将其忽略。将铲斗材料设置为Q345,建模完成后,可知铲斗质量为569.482 kg。使用命令流建立的铲斗模型如图4所示。

图4 铲斗三维模型
在铲斗与斗杆的铰点处施加全约束。对铲斗施加载荷时,分别将各段轨迹中的极限挖掘力的切向力、法向力、阻力矩作为外载荷。为防止出现由于应力集中而导致过大的计算误差,将所受的集中力转化为分布在多个节点的分力加载在斗齿的多个节点上。经仿真计算可以得到各段轨迹中铲斗应力、变形随铲斗夹角、斗杆夹角变化的情况,如图5所示。
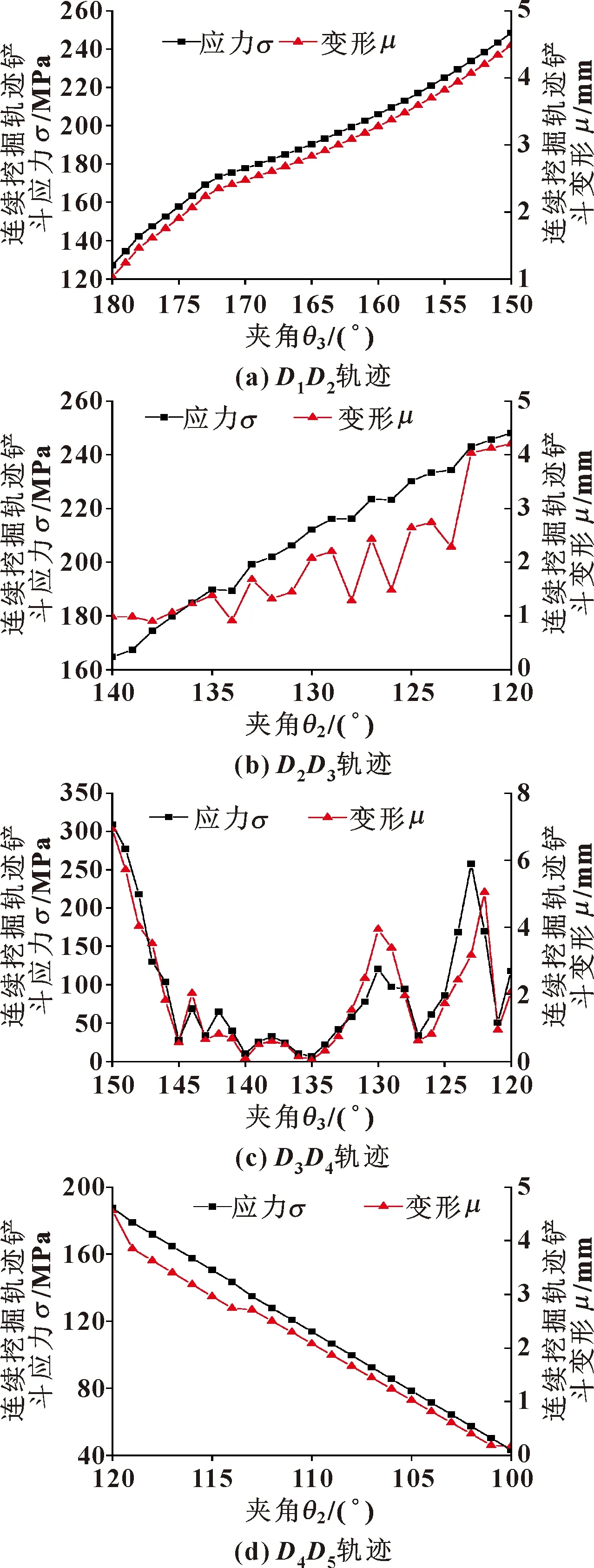
图5 铲斗结构强度
由图5可知:铲斗应力、变形随夹角的变化而变化。经与图3对比,铲斗应力与极限挖掘力切向力的变化趋势一致;图5中铲斗变形主要趋势与应力变化情况基本相同,由于受极限挖掘力的法向力和阻力矩的影响,铲斗变形随夹角的变化趋势偶尔出现波动,变形的波峰波谷出现位置与法向力拐点出现的位置相同。整条轨迹中,铲斗处于挖掘点时的应力、变形最大,此时,铲斗夹角为150°,应力、变形的具体情况如图6所示。

图6 挖掘点D3铲斗应力与变形
在连续挖掘轨迹中,铲斗应力、变形较大的位置相同。如图6所示:铲斗应力较大部位为背板、耳板与斗后壁板的焊接处,挖掘点铲斗的最大应力为302.283 MPa;铲斗变形较大的位置出现在切削刃板中间位置,轨迹中铲斗的最大变形为6.531 mm。
3 铲斗优化模型
3.1 优化目标
铲斗整体结构优化是三维层次的优化,涉及到了具体的挖掘工况,铲斗最大应力是否小于材料屈服强度对挖掘机工作效率有很大的影响。因此,将铲斗最大应力作为优化目标1。当挖掘机发挥的挖掘力不变、切削同样体积的物料时,铲斗与物料的总质量越小,越能节约生产成本,又由于铲斗所有材料都设为Q345,密度一致,所以将质量作为优化目标2。从而得到铲斗结构的多目标优化函数:
min()=+
(1)
其中,+=1,且、为正实数。在此,直接令==0.5。
3.2 设计变量
选取铲斗的切削角、斗底弧线半径、斗后角、切削半径等结构参数作为设计变量。即:
=[,,,]=[,,,]
(2)
3.3 约束条件
3.3.1 基础约束
选取原铲斗中切削角、切削半径、斗后角、斗底弧线半径数值加减10%作为优化区间,如表2所示。

表2 铲斗参数取值范围
3.3.2 性能约束1
将铲斗质量的变化量作为性能约束代入结构优化中,在优化后,铲斗质量的变化量应大于5%,约束表达如下式:

(3)
3.3.3 性能约束2
将铲斗最大应力作为性能约束2代入结构优化中,优化后的最大应力应小于优化前,约束表达如下式:
()=<[]=302.283 MPa
(4)
3.4 优化模型
综上,铲斗整体的多目标结构优化模型如下:

(5)
4 优化结果分析
此次优化使用的方法为遗传算法,铲斗结构优化具体内容为:(1)编写铲斗质量计算公式,并输入MATLAB遗传算法工具箱;(2)设置参数取值范围;(3)编写约束程序;(4)求解符合质量约束的结果;(5)调用APDL程序,对比此结果是否满足应力约束条件;(6)若满足,则优化完成;不满足,继续使用遗传算法求解,直至得到理想结果。优化后,铲斗结构参数、优化评价指标、最大应力的对比结果分别如表3、表4和图7所示。

图7 优化后铲斗应力

表3 优化后铲斗参数对比

表4 优化后铲斗评价指标对比
由表3可知:4个设计变量中切削角降低了85,斗后角增长了365,斗底弧线半径增长了8.33%,切削半径降低了4.35%。由表4可知:最大应力降低了6.23%,质量降低了5.27%,优化目标降低了6.25%。
由图7可知:优化前后铲斗应力集中区域的位置并未发生改变,最大应力由优化前的302.283 MPa降低为283.45 MPa,减少了6.23%。此次优化结果符合预期要求。
5 结论
基于连续轨迹理论选择了一条由4段分轨迹组成的连续挖掘轨迹,计算并分析了该轨迹上铲斗、斗杆液压缸极限挖掘力的数值变化规律,当斗齿尖处于挖掘点时,铲斗液压缸的极限挖掘力最大。
使用APDL语言建立了铲斗参数化模型,以极限挖掘力为外载荷对铲斗结构强度进行了计算,对比分析了铲斗应力、变形规律和分布情况,挖掘点的铲斗应力、变形最大,因此,在此工况下对铲斗进行优化。
以降低铲斗质量和最大应力为优化目标,选取多个铲斗结构参数作为设计变量,建立了铲斗轻量化优化模型,使用遗传算法进行优化,优化后铲斗质量和最大应力明显减小,验证了优化方法的可行性。

