轨道交通U形截面预应力混凝土连续梁的结构设计与分析

林 颖,张 阳,郑 辉

(1. 保利长大工程有限公司，广东 广州 510620；2.湖南大学，湖南 长沙 410205；3.湖南工业大学，湖南 株洲 412000)

1 概述

简支U梁结构[1]由于其能有效地降低建筑高度，同时具有外形简洁、降噪效果好、综合总价低等特点，在城市轨道交通高架结构中应用越来越广泛[2]。但简支U梁结构跨径较小，一般为30 m左右，在跨越道路、河流等障碍时，一般采用具有较大跨越能力的连续箱梁结构。连续箱梁与简支U梁在梁高上的巨大差别，致使结构过渡景观效果较差。为了解决连续箱梁与简支U梁的过渡问题，一种结合了连续箱梁与简支U梁为一体的连续U梁结构在工程实践中逐渐被采用[3]。

在实际工程项目中，通常采用简化方法对连续U梁进行分析和设计。在纵向分析中采用平面杆系模型进行分析和计算，确定结构的主要构造与纵向预应力布置形式，这种分析方法没有考虑纵向和横向弯曲之间的相互作用，以及在偏心荷载下的翘曲、变形和剪力滞效应[4]。本文以某地铁高架工程(30+45+30)m连续U梁为工程背景，通过建立三维有限元模型，将梁单元计算结果与三维有限元分析结果进行对比，评估采用简化分析方法的误差程度，为今后类型的连续U梁结构设计提供参考[5-6]。

2 工程概况

南京至句容城际轨道交通由南京东部的马群枢纽向东至句容的跨市域线路，是连接南京和句容市的都市圈线路。线路全长43.642 km，其中高架段长约26.866 km，高架区间标准结构为30 m简支U梁。本高架区间在跨越横向道路和河流时，设置了多座节点桥梁，主跨跨径为45～60 m。跨越宝华山路时，考虑与相邻简支U梁衔接的景观性要求，跨越宝华山路节点采用(30+45+30)m连续U梁结构。

图1 (30+45+30)m连续U梁结构Figure 1 (30+45+30) m continuous U beam structure

2.1 结构尺寸

(30+45+30)m连续U梁边跨与中跨跨中梁高均为1.84 m，边支点处梁高2.04 m，该处底板局部加厚0.2 m，中支点处梁高3.4 m，梁高变化段14 m，梁高为1.84～3.4 m，通过底板变厚实现(0.3～1.86 m)，底板变高段采用1.8次抛物线过渡。主梁上开口宽10.48 m，跨中底板厚0.3 m，边支点局部加厚至0.5 m。边腹板厚0.4 m，中腹板厚0.6 m；边腹板上翼缘宽度1.03 m，中腹板上翼缘宽度1.4 m。连续U梁横断面布置如图2所示。

2.2 预应力钢束布置

(30+45+30)m连续U梁采用全预应力结构进行设计，纵向预应力钢束采用抗拉强度标准值为1 860 MPa的高强低松弛钢绞线，公称直径15.2 mm。钢绞线的弹性模量：Ep=1.95×105 MPa，锚下张拉控制应力为1 302 MPa。连续U梁钢束横断面布置如图3所示。

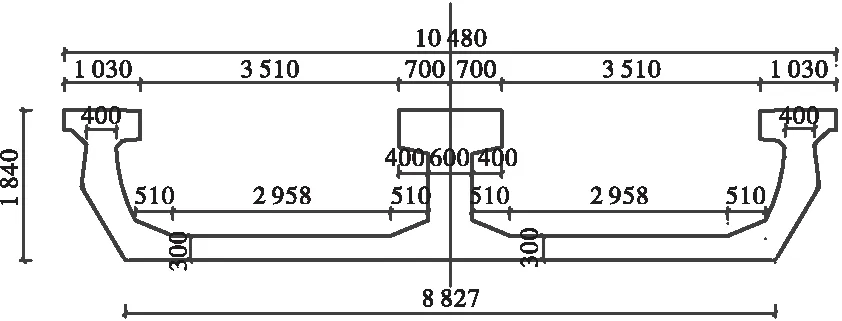
(a) 跨中截面

(b) 中支点截面

(a) 跨中截面

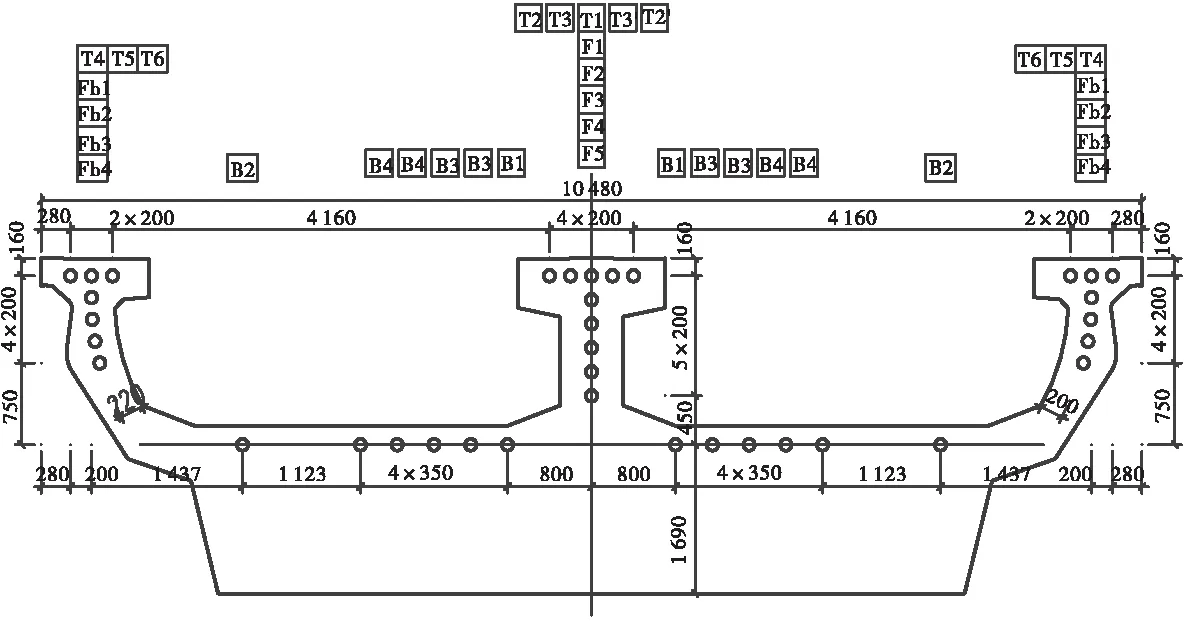
(b) 中支点截面

3 连续U梁计算模型

连续U梁在设计中通常采用平面杆系模型进行分析和设计，本文采用Midas civil软件，建立了(30+45+30)m连续U梁的平面杆系模型(见图4)，模型单元数58个，节点数59个。

图4 单梁计算模型Figure 4 Truss FEA model of continuous U beam

由于连续U梁为开口截面，截面抗扭刚度较小，使得桥梁空间效应明显，力学特性较为复杂，采用平面杆系模型难以准确分析结构实际受力情况。本文同时采用Midas FEA软件，建立了(30+45+30) m连续U梁的实体模型(见图5)，模型单元数90 569个，节点数66 627个。模型中采用实体单元模拟混凝土结构，混凝土弹性模量Ep=3.65×104 MPa，泊松比0.2，单位重量26.5 kN/m3。利用桁架单元模拟预应力钢束，在钢束梁端施加实际的有效预应力作为荷载。模型建立以分析结构的实际尺寸、材料类型、边界条件和荷载条件等为依据，尽可能准确地模拟结构实际情况[7]。

图5 U梁实体计算模型Figure 5 Three dimensional solid model of continuous U beam

4 连续U梁计算结果分析

4.1 正应力分布规律分析

对于连续U梁的平面杆系计算模型，在主力荷载作用下，梁单元截面上缘正应力如图6所示，下缘正应力如图7所示。从图中可以看出，主力荷载作用下，连续U梁全截面受压，截面最小压应力2.8 MPa。

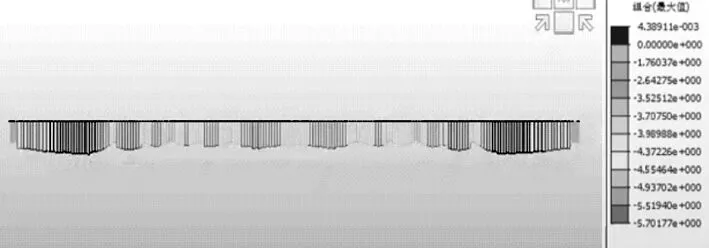
图6 连续U梁上缘正应力(单位：MPa)Figure 6 Normal stress on the upper edge of continuous U beam(Unit:MPa)

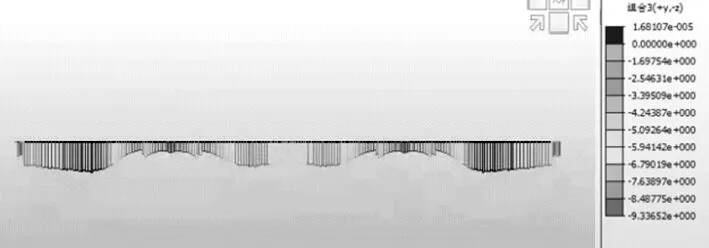
图7 连续U梁下缘正应力(单位：MPa)Figure 7 Normal stress on the lower edge of continuous U beam(Unit:MPa)

由于连续U梁为开口截面，截面抗扭刚度较小，空间效应明显，单纯依靠平面杆系模型，不能够准确地分析结构的受力状况。为了保证结构的受力安全，还需要对连续U梁结构进行三维实体模型分析，研究连续U梁的截面应力分布规律，并对平面杆系模型和三维实体模型主要截面计算结果进行对比，调整平面杆系模型的安全储备。

连续U梁的设计中，计算关键截面一般包括边墩支点截面、边跨跨中截面、中墩支点截面，及中跨跨中截面。主力作用下连续U梁的关键截面上的纵向正应力云图如图8所示。

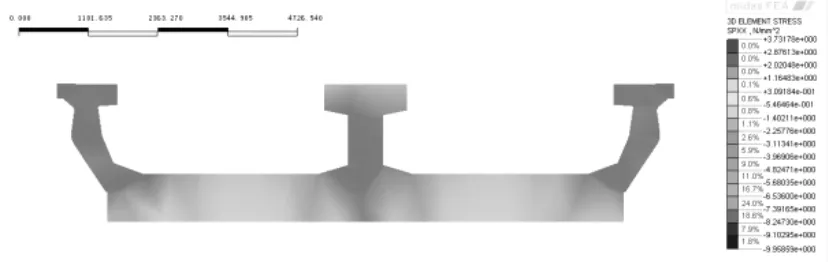
(a) 边墩支点截面纵向应力图

(b) 边跨跨中截面纵向应力图

(c) 中墩支点截面纵向应力图

(d) 中跨跨中截面纵向应力图

通过应力云图可以看出，除边墩支点和中墩支点支座位置由于边界条件的原因，局部应力失真，应力分布不均匀，其他位置应力分布较为均为。在主力荷载作用下，连续U梁全截面受压，压应力储备较大。并且，通过应力云图也可以看出，截面正应力在梁高度方向是呈线性分布的，截面满足平截面假定原则，可依据初等梁理论建立杆系模型进行计算。

本文在考虑相同荷载作用下，分别提取平面杆系模型和实体单元模型纵向应力结果进行对比，对比结果如表1所示。

表1 纵向正应力对比Table 1 Comparison of longitudinal normal stress

通过表1可以看出，平面杆系模型的纵向正应力计算结果与实体模型的纵向正应力计算结果的最大误差为27%，实体模型在顶、底板的最大、最小应力相对杆系模型更为不利，因此在设计时，对于平面杆系纵向正应力计算结果，建议考虑1.2～1.3的安全储备。

4.2 主应力分布规律分析

在恒载作用下，实体单元模型主应力云图如图9、图10所示。

图9 连续U梁主拉应力云图(单位：MPa)Figure 9 Cloud diagram of main tensile stress of continuous U beam (Unit:MPa)

图10 连续U梁主压应力云图(单位：MPa)Figure 10 Cloud diagram of main compressive stress of continuous U beam(Unit:MPa)

可以看出，除支点截面受支座影响外，其余截面主拉应力水平较低，最大主拉应力为-1.24 MPa。最大主压应力出现在中跨四分截面位置，最大主压应力为10.97 MPa。实体单元模型与平面杆系模型主应力计算结果对比如表2所示。

表2 主应力计算结果对比Table 2 Comparison of calculation results of principal stress

通过表2可以看出，实体单元模型与平面杆系模型的主应力计算结果基本吻合，设计时采用平面杆系模型的主应力计算结果是可行的。

4.3 局部受力特性分析

a.剪力滞效应分析。

由于预应力混凝土连续U梁为开口薄壁构件，截面抗扭刚度较小，在荷载作用下道床板容易出现剪力滞现象。故有必要对连续U梁各关键截面的道床板剪力滞效应进行分析。本文利用三维实体模型，对连续U梁各控制截面在恒载作用下道床板上缘的纵向正应力沿横向方向的分布进行研究，见图11，道床板横向位置起点为截面中心位置。

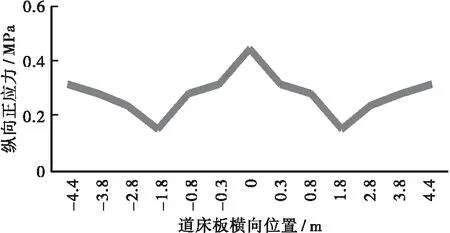
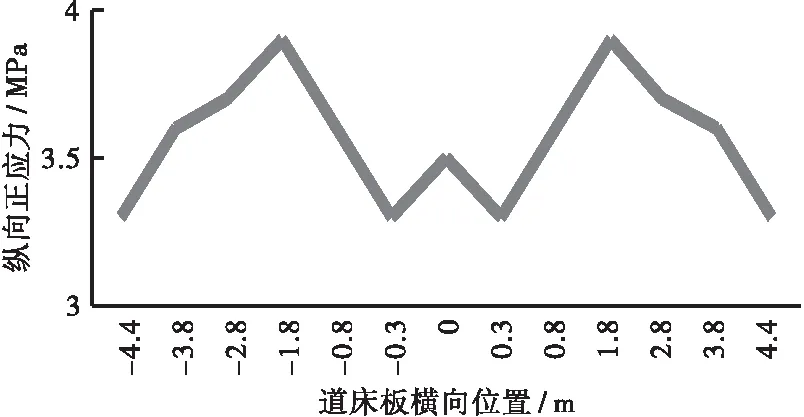
(a) 边支点截面(b) 中支点截面

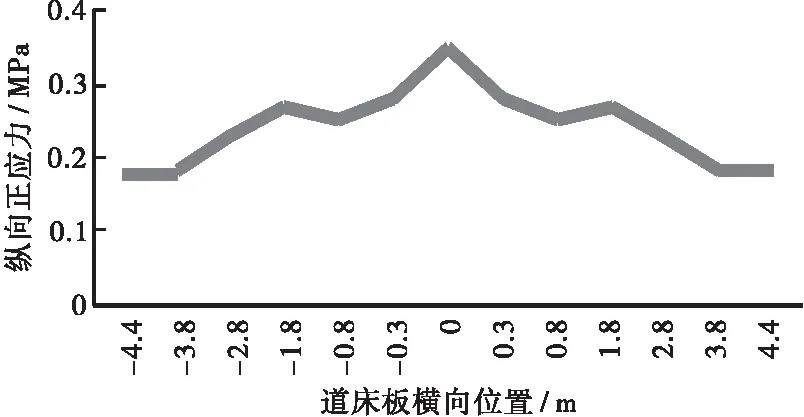
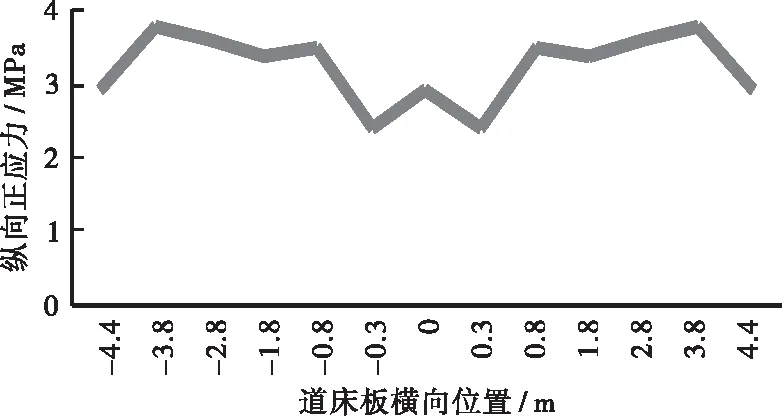
(c) 中跨1/4截面(d) 中跨跨中截面

从图11可以看出，由于剪力滞的影响，中跨跨中截面道床板纵向正应力的分布趋势为中腹板位置小、边腹板位置次之、轨道中心线位置较大，其主要原因是轨道中心线附近受两侧U梁腹板的约束作用较小，在正弯矩作用下发生了较大的局部变形。对于中跨1/4截面，由于其处于正负弯矩交界点附近，其正应力分布表现出中腹板位置偏大的现象。对与支点截面，道床板受到支座约束的影响，最大应力出现在支座位置附近。

b.腹板竖向剪力分析。

由于连续U梁为开口截面，主梁截面的不同腹板的横向受力均可能存在差异，整个截面腹板的剪力分配对主梁的横向设计有非常重要的指导意义。本文利用三维实体模型，对连续U梁截面的边腹板、中腹板、箱梁在恒载作用下承担的剪力值进行了量化分析。通过对截面各部位的剪应力进行积分，可得到各部位所承担的剪力大小。在恒载作用下，连续U梁各截面剪力计算结果如表3所示。

从表3可以看出，对于U形与箱形的组合截面，箱梁部分承担了大部分的剪力，在中支点附近，箱梁部分承担了约93%的剪力，截面设计时，应加强箱梁部分的横向抗剪设计。对于U型截面，中腹板承担的剪力值相对于边腹板，增大约5%。

4.4 结构刚度分析

在恒载作用下，实体单元模型的竖向挠度图如图12所示。从图可以看出，中跨跨中截面最大竖向挠度值为20.1 mm，边跨跨中最大竖向挠度值为8.3 mm。

本文在恒载工况下，分别提取平面杆系模型和实体单元模型竖向挠度结果进行对比，并同时对比了实际工程在全桥附属结构施工完成后的监测挠度，对比结果如表4所示。

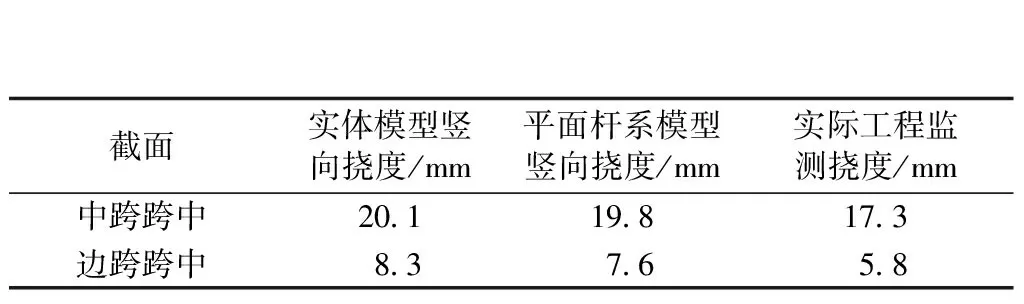
表4 恒载作用下竖向挠度对比Table 4 Vertical deflection comparison under dead load

通过表4可以看出，实体单元在恒载作用下的竖向挠度计算结果比平面杆系单元的竖向挠度计算结果稍大。实际工程由于未考虑徐变的影响，位移监测结果相对计算结果偏小。在实际项目设计中，可直接采用平面杆系模型的竖向挠度计算结果。

5 结论

以某工程实例(30+45+30)m连续U梁为背景，通过三维有限元模型分析了连续U梁纵向正应力和结构刚度，并与平面杆系单元计算结果进行了对比，得到结论如下：

a.连续U梁平面杆系模型的纵向正应力计算结果与实体模型的纵向正应力计算结果的最大误差为27%，实体模型在顶、底板的最大、最小应力相对杆系模型更为不利，因此在设计时，对于平面杆系纵向正应力计算结果，建议考虑采用1.2～1.3的安全系数。

b.连续U梁结构为开口薄壁构件，在竖向荷载作用下空间效应明显，应力分布不均匀，道床板中正应力表现出明显的剪力滞效应，在支点截面更为明显，设计时应加强该处的强度计算和钢筋配置，从而控制截面的局部应力。

c.实体单元模型与平面杆系模型的主应力计算结果基本吻合，设计时采用平面杆系模型的主应力计算结果是可行的。

d.实体单元在恒载作用下的竖向挠度计算结果比平面杆系单元的竖向挠度计算结果稍大。实际工程由于未考虑徐变的影响，位移监测结果相对计算结果偏小。在实际项目设计中，可直接采用平面杆系模型的竖向挠度计算结果。

e.连续U梁作为开口薄壁截面，受力情况较为复杂，计算时采用平面杆系模型进行整体受力分析后，建议采用三维有限元模型对连续U梁进行局部应力分析，对连续U梁应力集中部位进行适当的补强，防止连续U梁在运营过程中出现裂缝。