塌岸和库水位变动作用下路基边坡稳定性研究

胡盛华，毛 敏

（1.云南省交通运输厅工程质量监督局，云南 昆明 650214；2.山西省交通科技研发有限公司，山西 太原 030032）

0 引言

随着我国对水资源的利用不断增加，各地建立了许多大大小小的水库，许多地质问题也随之而来，水库塌岸便是其中之一。与此同时，公路工程建设逐渐由东部沿海地区向中西部地区转移，不可避免地穿越西南水文地质条件复杂的库区。为保证水库蓄水后高速公路运营的足够安全，在工程建设的整个过程中将塌岸的影响纳入考虑范畴具有重要意义。

目前主要基于半经验半理论的模式对水库塌岸预测方法进行探索。前苏联学者萨联斯基最早对水库塌岸的预测方法进行了研究。随后国外学者提出了卡丘金法[1]、佐洛塔寥夫法[2]等，国内有王跃敏提出的两段法[3]、许强提出的岸坡结构法[4]、彭仕雄提出的冲堆平衡法[5]等。实际操作中应结合具体工程地质条件对以上方法进行选用。塌岸的发生对库岸路基安全性产生的威胁一直受到相关研究者和工程技术人员的关注。边义成（2007）采用规范方法对讨赖河东水峡水电站库区右岸铁路路基塌岸宽度分别进行了短期和长期的预测[6]。张建明等（2013）利用图解法对山区冷清公路路基岸坡进行了预测，并提出了治理方案[7]。王峰（2014）基于S211线愚公山段路基岸坡再造防治方案，探索了新的针对性措施[8]。王忠武等（2020）采用多种塌岸预测方法对某沿江高速公路路基塌岸的范围进行了预测，并结合Geostudio软件对边坡稳定性进行了分析，给出了路基受影响的建议范围[9]。

综合以上可以看出，近年来关于威胁路基工程的塌岸研究大多关注于其预测方法和防治措施。本文以白鹤滩水库沿岸新建的高速公路为例，选取典型的塌岸路段，结合实际的工程地质条件，基于两段法对研究路段进行塌岸范围预测的结果，利用软件对不同工况下的高速公路路基边坡稳定性进行分析，研究塌岸联合库水位升降条件下的路基边坡的渗流稳定性及其对路基安全性可能造成的威胁。

1 工程地质条件

东川格勒至巧家葫芦口高速公路，路线起于云南省东川区格勒镇大田坝上游1.2 km附近，沿小江右岸至金沙江右岸展线。受区域内小江断裂带活动的影响，线路通过区的小江-金沙江河段河谷岸坡岩土体普遍较为破碎，再加上受到自然界诸多不利因素干扰，库岸边坡风化程度进一步加深，岩土体物理力学性质降低。

研究区段里程桩号位于格巧高速K3段，地质纵断面图如图1所示，根据调查资料，上覆地层以第四系残坡积（Q4el+dl）碎石土、冲洪积（Q4al+pl）、崩坡积（Q4col+dl）碎、块石土等为主。同时该段在金沙江白鹤滩水电站库区内，库区为年调节水库，最大蓄水位为825 m，防洪限制水位为785 m，死水位为765 m，年水位变幅达60 m。水库建成后，水库水位升降引起的动水压力的变化造成的边坡崩塌、滑移，可能会使边坡产生一定程度的塌岸，对高速公路运营安全造成影响。

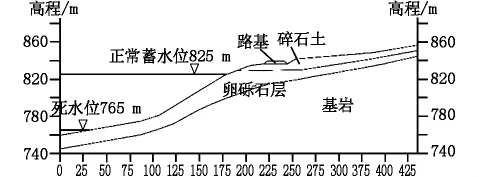
图1 边坡主剖面地质纵断面图

2 塌岸与库水位联合作用下的路基边坡渗流稳定性特征

2.1 塌岸预测

结合实际工程地质条件和参考资料，可知两段法（图2）更适合于具有库面较窄，风浪作用较小，岸坡地层为黏性土、砂性土、碎石类土、弃碴及岩石的全风化地层和有较完整水文气象资料等条件的我国南方山区峡谷型水库[10]。

图2 两段法示意图

根据现场实测资料，研究路段水下休止角为28°，水上休止角为37°，毛细水上升高度取1.5 m，由于设计低水位的原始坡脚小于水下休止角，所以将A点上移至原始坡脚大于水下休止角的位置。

依据两段法原理作图3，得到塌岸范围为22.28 m。塌岸前后剖面图用于渗流稳定性分析。

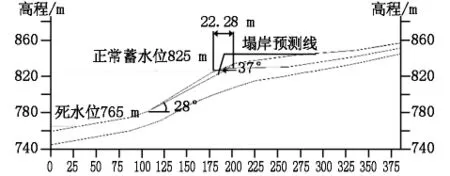
图3 两段法预测塌岸图解

2.2 塌岸前后路基边坡渗流特征

2.2.1 边坡渗流分析原理

由于受到库区水位运行作用的影响，路基边坡部分岩土体处于饱和-非饱和交替状态。本文研究为松散碎石土和卵砾石层构成，粒径大、孔隙多，因而边坡对库水作用十分敏感。与前人仅考虑塌岸范围或单考虑路基边坡稳定性所不同的是，本文分别对塌岸前后边坡的渗流进行分析、对比。松散坡积层滑塌后边坡结构，包括坡形、坡高、坡度等均会发生变化，原本被覆盖的下层岩面裸露，岩土体材料性质也可能改变，与此同时，渗流工况的改变会导致边坡稳定性的变化。因此对塌岸前后边坡的渗流过程进行分析是十分必要的。非饱和渗流的重要任务之一是非饱和渗流基本微分方程的求解，研究中涉及的是X、Z方向的二维渗流问题，控制方程如式（1）：

式中：h为总水头；t为渗流时间；θw为体积含水量；kx、ky、kz分别是 X、Y、Z 方向的渗透系数。

对于稳态渗流，单位时间内流入量等于流出量，因此稳态渗流控制方程如式（2）：

对于瞬态渗流，假定总应力不变、孔隙气压力ua不变，可得瞬态渗流微分方程：

式中：γw为水的比重；mw为储水曲线的斜率，可由土水特征曲线获取。

求解稳态渗流微分方程，只需添加初始边界条件。对于瞬态渗流微分方程的求解，则需要基于稳态分析的结果另行添加随时间变化的边界条件。

2.2.2 计算模型

在软件中分别导入塌岸前和塌岸后的边坡区域，并进行网格划分（图4、图5）。其中基岩作为不滑动层，在渗流稳定性分析中不予考虑。

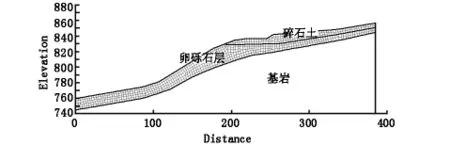
图4 塌岸前边坡网格划分模型

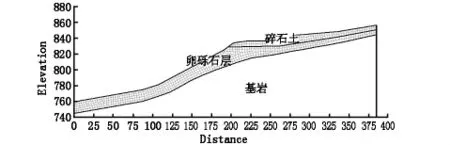
图5 塌岸后边坡网格划分模型

2.2.3 计算参数和边界条件

边坡岩土体的物理力学参数通过现场勘察和工程类比法确定，如表1所示。

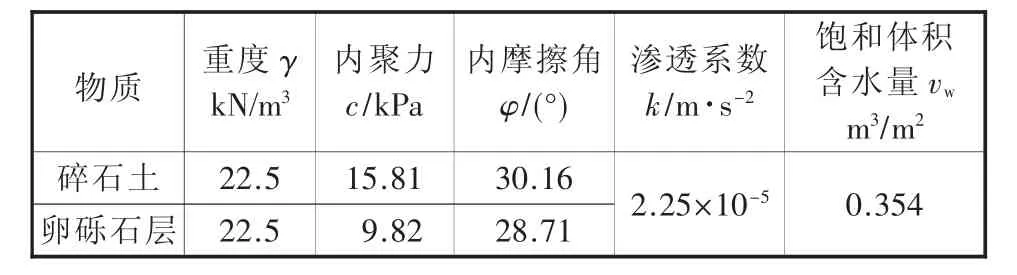
表1 土层土体的物理力学性质

已知饱和土水含量，非饱和土的土-水特征曲线采用软件自带的样本函数估计的方法获得。非饱和土的渗透系数曲线根据Fredlund和Xing经验公式确定。

该研究以白鹤滩库水一年的库水位升降为计算工况，边坡表面765 m至825 m高程根据库水位调度图（图6），设定随时间变化的总水头边界。

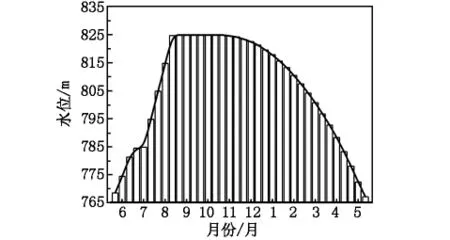
图6 水库水位调度模式

2.2.4 塌岸前后渗流特征

库水位到达最高蓄水位825 m后保持稳定，直至第81 d开始降水，第275 d水位降到最低后，水库水位开始上升。对于蓄水阶段，选取第275 d开始每5 d的零水压力线进行展示（图7、图8）；对于降水阶段，选取从第80 d开始每10 d以及第275 d的零水压力线（即边坡内部地下水位线）进行展示（图9、图10）。

图7 塌岸前库水位上升阶段地下水位线

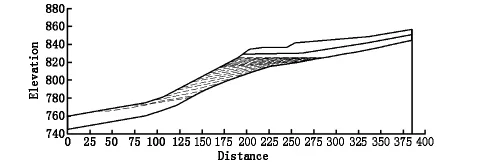
图8 塌岸后库水位上升阶段地下水位线

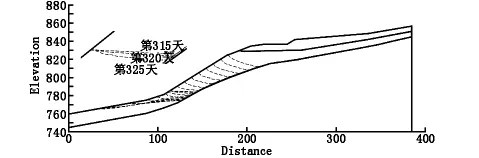
图9 塌岸前库水位下降阶段地下水位线

图10 塌岸后库水位下降阶段地下水位变化

分析结果发现，塌岸发生前和发生后的库水位涨落阶段，边坡内部地下水位线变化相较于库水位涨落总存在滞后现象，且库水位涨落速度越快，地下水位变化滞后现象越明显。具体表现为库水位变化阶段不同，同一水位高度地下水位线不同。在第80 d到275 d的库水位下降阶段，地下水位线后缘总是高于坡面的库水位高度，且距离坡面越远越明显，此时地下水向外排泄；第275 d后库水位开始上涨，而水位上涨初期第275 d到300 d，地下水位线后缘高于水位高度，边坡内地下水仍然向外排出。同时，库水位下降阶段交替到库水位上升阶段时边坡地下水位变化滞后，第275 d到第300 d地下水位线出现了相互“交叉”，而后随着水位升高，地下水位线后缘逐渐低于水位高度，此时地下水由向外排泄转为向边坡内渗流。第315 d到325 d库水位维持在785 m未发生改变，地下水位线后缘逐渐抬升与库水位平齐，这是因为库水向边坡内渗透补充了地下水位。

对比塌岸前后各时间步长的地下水位线，发现塌岸的发生对渗流特征的影响不大。

2.3 塌岸前后路基边坡稳定性特征

2.3.1 塌岸前后稳定性系数变化分析

对塌岸前天然条件（未蓄水）下和825 m正常蓄水条件下的边坡进行稳定性分析（图11、图12）。

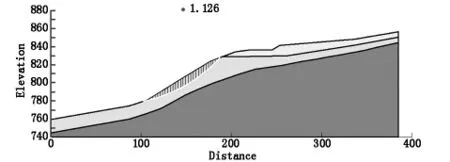
图11 塌岸前未蓄水工况下静态边坡稳定性分析结果

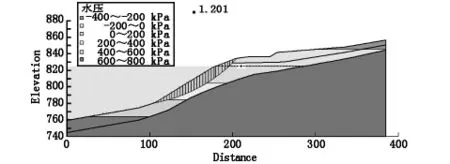
图12 塌岸前825 m正常蓄水工况下静态边坡稳定性分析结果

水库在天然状态下，由于土体干燥，没有库水的影响，边坡的最危险滑移面范围较小；在水库蓄水后，受到库水影响，最危险滑移面范围扩大，同时稳定性系数从1.126增加到了1.201，这说明水库开始正常运营后，边坡稳定性会有所提升，这是由于库水作用下静水压力增加，起到了一定的压脚作用。

库区边坡因为地下水与岩土体之间发生的复杂的物理化学作用，而与其他非库区边坡不同[11]。库水位随时间的变化引起库水在边坡内部发生渗流运动，从而导致边坡内部地下水位、孔隙水压力分布和基质吸力等发生变化，最终使得边坡的稳定性系数发生变化（图13）。需要说明的是，研究中以塌岸前后825 m正常蓄水条件下的最危险滑移面作为指定滑移面进行计算。

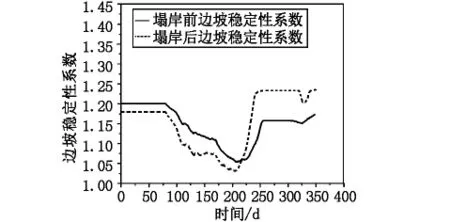
图13 塌岸前后边坡稳定性系数随时间变化曲线

对比塌岸前后边坡稳定性系数变化规律，发现塌岸的发生与否对边坡稳定性系数随时间变化的趋势影响不大。以塌岸前为例，在第80 d到210 d，库水位下降时用于反压坡脚的库水消失，边坡内地下水向坡外渗透，产生了指向坡外的渗透力，滑体的滑动力增大，抗滑力减小；同时，地下水位线下降滑体导致非饱和区的扩大，基质吸力增加，滑体的抗滑力增大，高水位期前者占主要作用，因此稳定性系数整体呈下降趋势。第210 d后，库水位仍处于下降期，而边坡稳定性系数逐渐增大，这是因为低水位期地下水位线逐渐趋于持平，渗透力减小，直至256 d库水位的变化尽管仍然会引起地下水位线的变化，但是此时地下水位线已经远离滑体范围，边坡稳定性系数便不再受其影响，即保持不变。

第275 d时库水位降低到最低蓄水位765 m后开始抬升，水位上升初期，因为地下水位线仍然位于滑体范围外，因此边坡稳定性系数依然保持不变。第305 d以后水库水位继续上升至超过滑体前缘高度，受水浮力的影响边坡稳定性系数降低。随时间推移，水库水位持续抬升，边坡受到的指向坡内的渗透力增大，静水压力也增大，因此稳定性系数随水位抬升而增大。

虽然塌岸前后边坡稳定性系数随时间变化趋势几乎一致，但是塌岸发生后边坡稳定性对库水位涨落工况更加敏感，即受同样的库水位涨落影响塌岸发生后稳定性系数变化幅度更大，这是因为塌岸发生后危险滑移面范围扩大，导致滑体受水位线和水压力变化影响范围扩大。

值得注意的是，岸前最低稳定性系数1.05大于塌岸发生后的1.03，塌岸的发生使得边坡最低稳定性系数有所降低。

2.3.2 塌岸前后边坡潜在滑移面范围分析

塌岸发生后边坡原有的力学平衡状态发生改变，为了评价塌岸发生后不稳定边坡对路基产生的影响，需要进一步考虑塌岸发生后的潜在滑移面与路基限界的相对位置关系。一般认为边坡稳定性系数小于1.25容易出现滑动，因此基于库水位涨落工况下渗流分析的结果，通过试算滑移面，分别计算了塌岸发生前后稳定性系数在0到1.25之间的潜在滑移面范围（图14，黑色部分）。

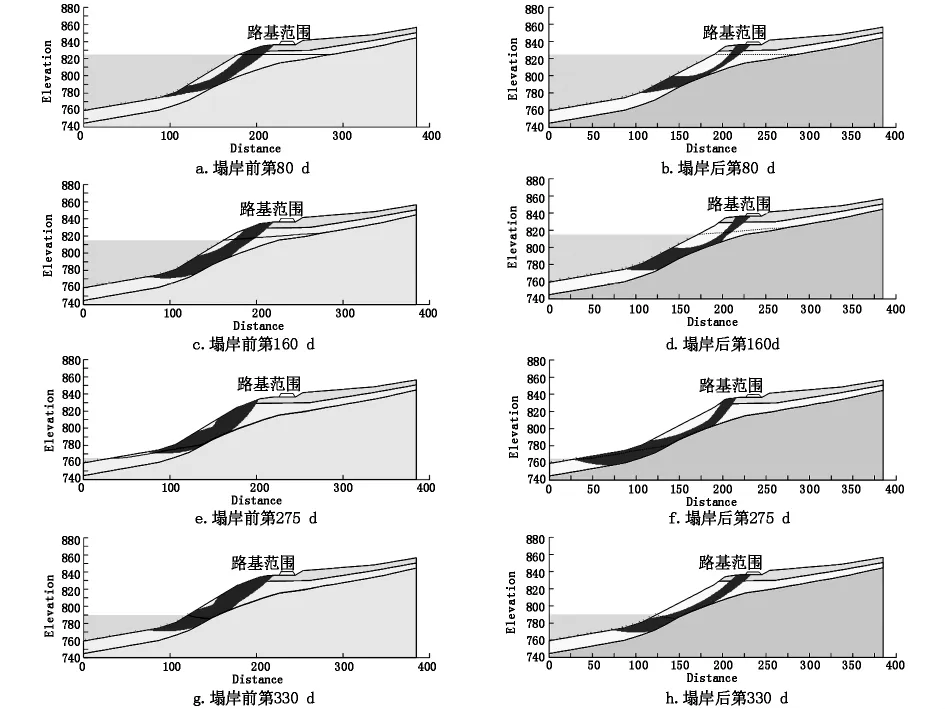
图14 塌岸发生前后选定时间步长潜在滑移面

结果显示，潜在滑移面范围变化与库水位涨落存在正相关性，即随着库水位下降潜在滑移面整体下移，随着库水位上升整体上移。

对比塌岸前后结果发现，在第80 d和第160 d，路基边坡在一系列外界因素影响下发生塌岸后，潜在滑动面会在一定程度上移，结合前文稳定性系数分析的结果可知塌岸发生后的静水期稳定性系数降低，同时降水前期边坡稳定性系数随着库水位下降的减小幅度大于塌岸发生前，因此塌岸发生后降水期路基边坡的不稳定对路基的安全运营造成了很大的威胁。与之不同的是，第275 d库水位上升阶段，虽然塌岸发生后滑移面上移，但是此时边坡稳定性系数大于塌岸发生前。

在已经研究了库水位以及塌岸对路基边坡的影响，研究结果发现，水库后期运行过程中，边坡稳定性会受到较大的影响。通过对比水库塌岸前后的水库岸坡失稳影响范围，发现塌岸发生后，边坡失稳会严重威胁到路基的安全。因此，修建库区公路时需要在考虑塌岸和库水位联合作用的基础上，采取合适的边坡防护措施对路基边坡进行防护。除此之外，路基在塌岸发生后的降水期安全性最低，这段时间可以采取必要的监测措施。

3 结语

本文以白鹤滩水库沿岸新建的高速公路工程为背景，选取典型的塌岸路段，通过收集相关的文献资料，结合实际的工程地质条件，基于采用两段法对塌岸范围进行预测的结果，利用有限元软件对不同工况下的高速公路路基边坡进行渗流稳定性分析，得到结论如下：

a）库水位升降过程中，路基边坡内地下水位线的变化存在明显的滞后性，相同库水高度，库水运行阶段不同，地下水位线也不同。同时，塌岸的发生对边坡渗流特征影响不大。

b）塌岸前水库开始正常运营后，边坡稳定性有所提升，这是由于水库水位上升后边坡土体受到静水压力的作用。塌岸发生后受库水位涨落的影响，路基边坡稳定性系数变化的幅度相较于塌岸发生前有所增大，最低稳定性系数降低。

c）塌岸前后路基潜在滑移面范围随着库水位下降而整体向下移动，反之亦然。塌岸发生后的降水期边坡稳定性系数减小幅度大，潜在滑移面侵入路基限界以内，是路基工程安全性最低的阶段，需要加以重视。

d）库区复杂地质条件下公路工程的设计不仅仅需要考虑短期内可能对安全性造成威胁的因素，还需要根据设计年限考虑塌岸等远期可能发生并影响公路运营的潜在危险。