基于灰色马尔科夫模型的电力电容器投标报价策略

罗林波，张 韬，罗岚波，伍 娟

（1.国网湖南省电力有限公司娄底供电分公司，湖南 娄底 417000；2.国网江西省电力有限公司电力科学研究院，江西 南昌 330096）

0 引言

如今，现代企业普遍以招投标方式规范企业采购行为。随着社会经济的发展，招投标所涉及的经济对象愈发大型化、复杂化，招投标行为多批次化，这给企业投标决策提出了新的挑战[1-2]。对于企业而言，如何制定并实施正确的投标报价策略，并以此为依据得出既有合理利润又有竞争优势的报价，关系着企业的经济效益乃至于企业的生存[3-4]。

国家电网有限公司评标采用综合评估法，分技术、商务、价格三个部分分别进行量化评审，根据具体的设备标的按权重比例汇总计算最终量化评审得分[5-7]。一般来说，在电容器类商品上，各公司在技术、商务方面实力基本相当，价格得分高低是企业能否中标的关键。文中对国家电网有限公司2013年至2014年的电容器招投标进行分析，以中标为目的，选择某公司作为目标公司，研究投标企业的投标报价策略。

1 基于灰色马尔科夫模型的货物均价预测

通过对2013 年至2014 年6 批电容器货物的货物数量和投标报价数据进行处理得到各批次货物的均值，由于各批次货物均值的变化可能呈现不规律性，故采用各类预测模型进行预测时，均需对其预测精度进行检验和评价。文中考虑结合马尔科夫模型对灰色预测的残差进行修正，从而进一步提高预测精度。

1.1 灰色预测模型

灰色预测模型一般用于对事物行为特征的发展演变趋势进行估计预测，以及对事件发生的未来时间分布情况进行研究等。这实际上是将事物发展的“随机过程”当作“灰色过程”研究，把“随机变量”当作“灰变量”。

灰色模型的检验方法包括残差检验，后验差检验和关联度检验，当通过全部检验时，才可以用来做预测，不能通过时，通过建立残差的修正模型来提高灰色模型的精度[8-9]。

1.1.1 GM（1，1）模型求解

GM（1，1）模型是灰色模型中一种特殊的线形动态模型，两个参数1 分别表示系统含有一个变量，即一阶单变量的微分方程模型。一般只需一个时间序列，4 个以上的连续数据就可以用于求解预测的GM（1，1）模型[10]。

1.1.2 GM（1，1）建模原理与方法

为了获取灰色预测模型所需的数据，先要对已有数据做预处理，得到累加生成序列。设原始数据序列为：

则累加生成序列为：

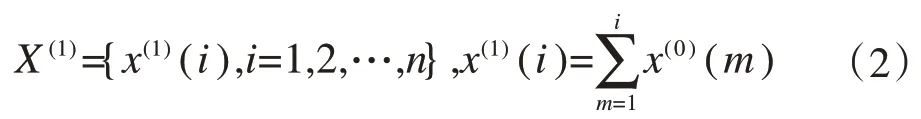
然后建立微分方程如下：

式中：X(1)为经过一次累加生成的数列；t为时间；a、u为待估参数，分别称为发展灰数和内生控制灰数。

利用最小二乘法求参数a、u。设

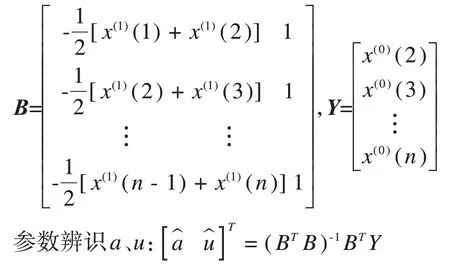
解微分方程后可以得到：

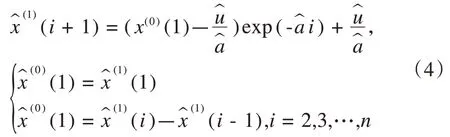
1.1.3 模型检验

灰色预测检验一般有残差检验、关联度检验和后验差检验。

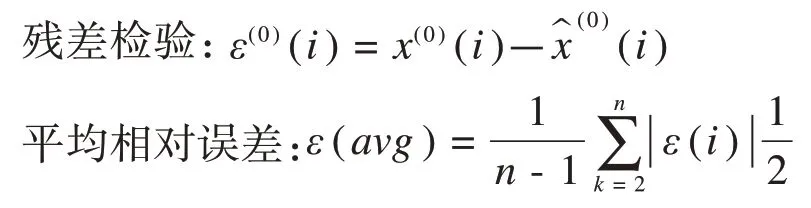
关联度检验：当ρ=0.5 时，关联度大于0.6 时认为通过关联度检验，否则关联程度不符合要求。其中关联度的计算公式：

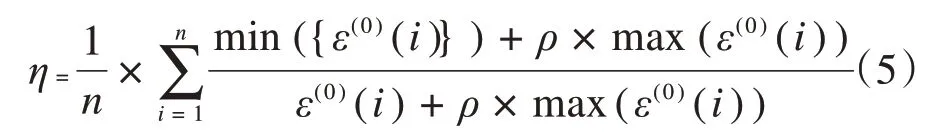
模型的后验差检验依赖于小误差概率P和后延验差比值C，按C和P两个指标，可以综合评定预测模型的精度，如表1所示，其中：

表1 后验差比值表

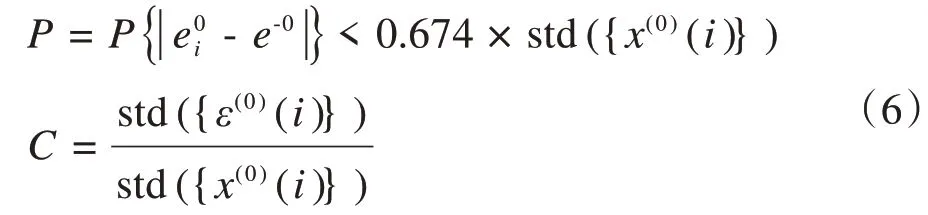
当P≤0.7 且C≥0.65 时模型不合格，其中std（·）表示标准差。

1.2 马尔科夫预测模型

1.2.1 马尔科夫链

某系统的行为特征存在一定规律性，其未来某一时间的特征只与当前时刻有关，而与过去的历史无直接关联，现实中普遍存在此类现象[11-13]。投标报价项目也存在这样的特点。第一，同配置包在不同批次中报价是不同的。第二，下一批各包的报价受当前报价以及历史批次报价的影响，其中影响最大的是当前批次报价。描述这类随机现象的数学模型称为马尔科夫链模型[14]。

假设随机过程序列{Xn，n≥0}，对于任意的n≥1，任一非负整数i1，j2，…in，i，j∈E，恒有P（Xn+1=j|X0=i0…，Xn-1=in-1，Xn=i）=P（Xn+1=j|Xn=i）），则称{Xn，n≥0}为马尔科夫链。如果N 为可离散集合，则称{Xn，n≥0}为离散参数的马尔科夫链。

设I为离散参数的马尔科夫链的状态空间，则称Pij为序列从状态i转移到状态j的概率，也称条件概率；若转移概率与实践起点m无关，则称此马尔科夫链为非齐次马尔科夫链，其状态转移矩阵可以表示为：

矩阵中元素非负，行和为1。

1.2.2 状态划分及修正

将一个具有马尔科夫特征的非平稳随机序列X(t)=x(0)(t)划分为s个状态Qi，i=1，2，…，s。任一状态表示为Qi=[Q1i，Q2i]，其中灰元Q1i，Q2i随时间t变化而变化，划分状态数s和Li，Ri可由预测值或根据具体情况而定为原始数据的均值[15]。

以ni表示处于i状态的频数，nij表示由状态i经过一步转移到状态j的频数，从而求出一步转移概率矩阵：

实际应用中可能用到的多步转移概率矩阵为Pn=Pn。

马尔科夫链预测是利用每年实际值状态变化来计算状态转移概率矩阵，从而得到预测值的方法，所以先把实际值按相对误差进行划分。{L1，L2，L3，L4}和{R1，R2，R3，R4}分别取其前四项和后四项，即得出本项目误差的4个状态：

各状态的相对误差见表2。

表2 各状态的相对误差取范围

1.3 灰色马尔科夫模型预测货物均价的检验和对比

采用灰色马尔科夫模型对各批次货物均价进行预测，其部分检验结果如表3。可见结果中原存的大量不合格预测已被修正为较好的预测值，故灰色马尔科夫模型足以满足货物均价的预测需求，可用于进一步分析计算。

表3 GM（1，1）和灰色马尔科夫模型预测结果对比

部分预测结果如图1所示。

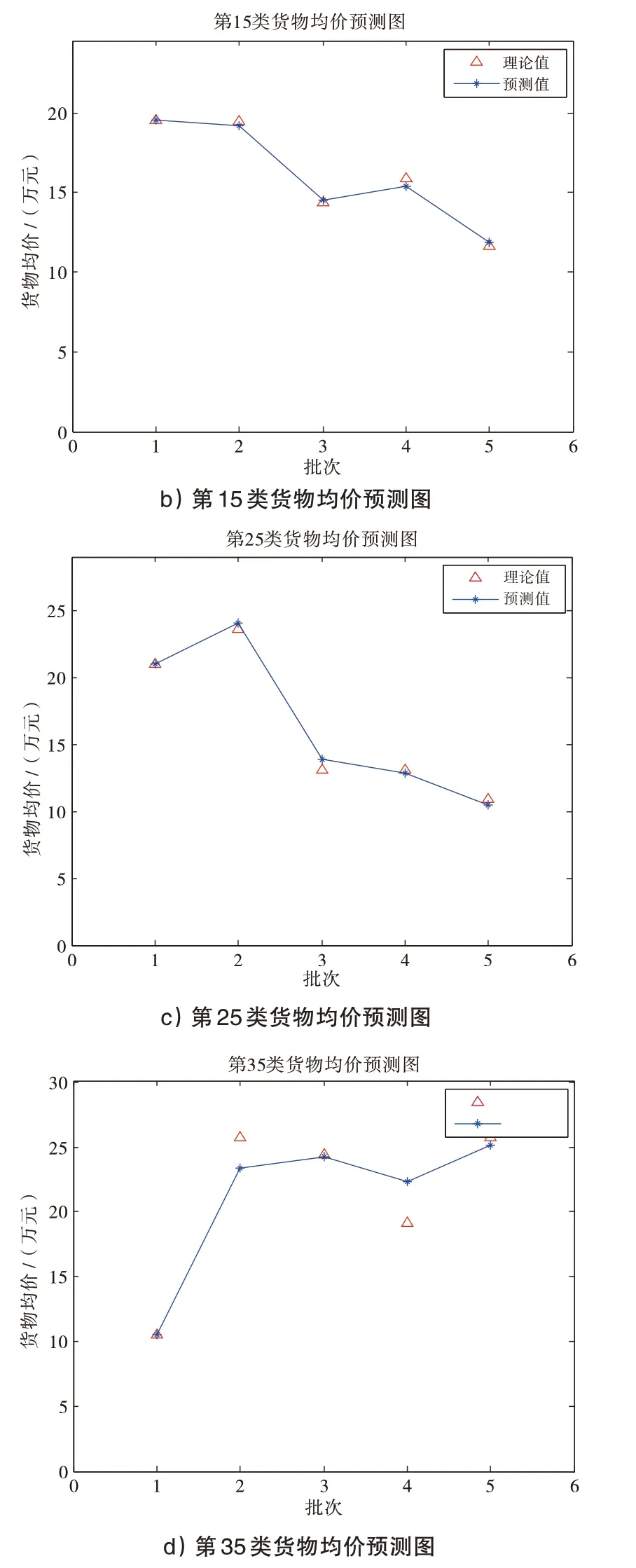
图1 第5、15、25与35类货物均价预测图

1.4 预测模型的优化

定义调整系数tz2，使：

可知各批次下存在一个tz2（t），使得目标公司的中标率g1和获得前三名的概率g2最优化。

针对前四批数据，计算得各批次下的tz2 与g1 的关系如下图所示。

图2 第1~4批招标调整系数与中标率关系图

各批次下的最佳tz2值统计如表4。

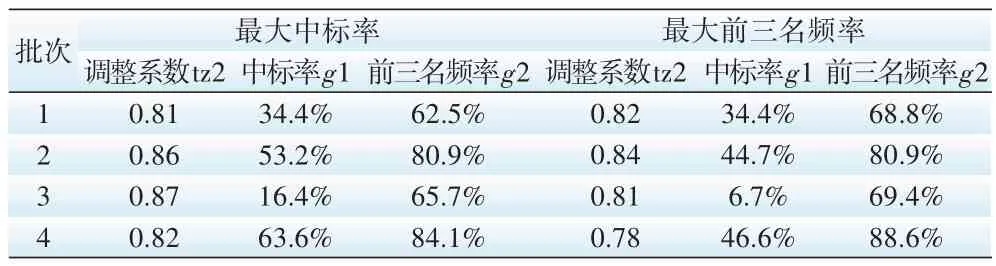
表4 g1和g2分别最佳化条件下的tz2值统计表

由表可知tz2 有较明显的线性变换规律，故可直接采用一次函数对其进行拟合，求得tz2（5）=0.846，如图3所示。

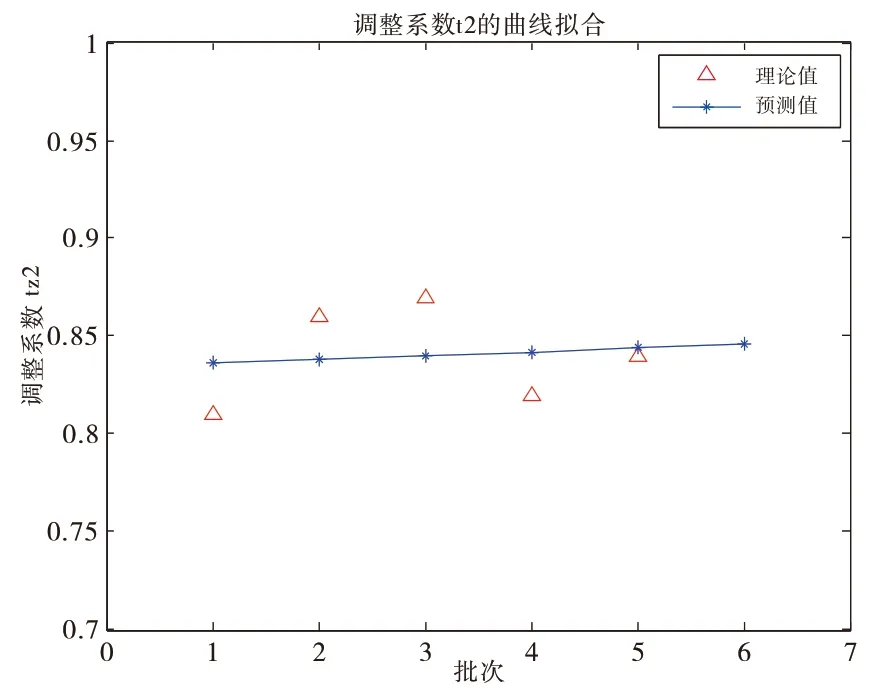
图3 调整系数曲线拟合图

此后可根据前4 批数据，结合调整系数tz2（5）对第5 批的投标情况进行预测，并与真实情况进行对比，从而实现该报价预测模型的检验。

2 预测模型的优化与检验

国家电网在2013 年至2015 年每年举行6 批电容器类货物招标，均采用综合评标法进行招标。而文中分析 2013 年至 2014 年的 6 批招标中，主要有 17 家公司参与竞标，各批次下浮比例及包数（经过数据预处理后）如表5。

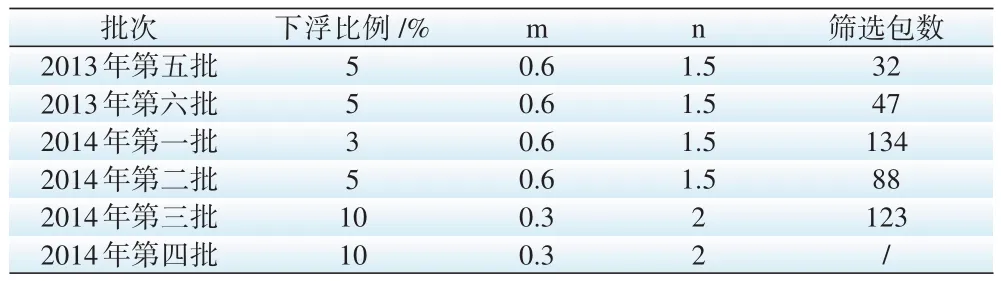
表5 各批次下浮比例及包数

通过马尔科夫分析，得到了历史数据中各包每类货物的平均价格，以此为基础建立了最优报价的数学模型，并进行了相关的改进和优化。为了验证该模型的正确性，选择2014 年第三批的具体情况进行分析和说明。将目标公司的实际报价与本模型的预测报价进行了对比，分别计算两种报价的中标情况，证明了本模型的实用性，如表6。

公司招投标的最终目的是中标，由于文中假设各厂的技术、商务等实力相当，价格得分排名成为了影响中标率的单一变量。表7是将实际报价和模型预测报价所得的价格分数进行了分析，并对中标率进行比较。从表中可以得知，文中所建立的价格预测模型相对于公司的自行报价在瞄准率上有了很大的提高，价格得分第一名的频率从1.63%大幅度提升到了20.33%，提高了将近12.5 倍；价格得分前两名的频率增长到41.46%，而前三名的频率从8.13%提升至50.41%，提高了6.2倍。采用本模型所预测的价格进行投标，使得目标公司前三名的瞄准率与其余16家公司（共17家公司参与竞标）前三名瞄准率之和相当。与公司的实际报价所得价格分数相比，有了质的提升。

表7 模型报价和公司实际报价中标率比较

3 结语

针对国家电网有限公司电力电容器的投标问题，利用往期数据，在灰色预测基础上进行马尔可夫预测，既可提升灰色预测在随机波动数据序列方面准确度，又可克服马尔可夫预测的局限性，该模型不仅考虑了数据序列中的演变规律，而且通过状态转移概率矩阵的变换提取数据中的随机响应，因此将二者结合起来将大大提高预测精度，为企业投标报价提供理论参考依据。