基于多项式正态变换和拟蒙特卡洛法的概率潮流计算

傅 明，童 超，单松兴，皮香香，杨 柳

（1.南方电网电力科技股份有限公司，广东 广州 510000；2.国网江西省电力有限公司电力科学研究院，江西 南昌 330096；3.国网江西省电力有限公司樟树市供电分公司，江西 樟树331200；4.国网江西省电力有限公司高安市供电分公司，江西 高安 330800；5.南昌科晨电力试验研究有限公司，江西 南昌 330096）

0 引言

风电出力具有强烈的波动性和不确定性，大规模风电并网将给电网的安全运行带来严峻挑战[1-2]。然而，确定性的潮流计算（Deterministic Power Flow，DPF）无法考虑风电出力的概率不确定性。概率潮流计算（Probabilistic Power Flow，PPF）将电网中的随机变量（如风电出力、负荷等）逐组代入确定性潮流计算模型，以获得潮流结果的矩信息、频率直方图和概率密度函数等，能够全面揭示随机变量对电网运行的影响。因此，研究PPF计算极具现实意义。

建立精确的输入随机变量概率模型是保证概率潮流计算准确性的关键。电网中的随机变量（如风电出力、负荷等）受到气象因素、地理环境等多种复杂因素影响，这些变量可能服从任意概率分布且分布间存在相关性[3]。然而，目前电网中随机变量常假设为常规概率分布，例如负荷一般当成正态分布[4-6]，风速往往用Weibull分布来模拟[7-9]；同时，利用NATAF变换建立概率分布间的相关关系。在少量运行场景中，上述建模方法可能具备一定的有效性。但实际电网中风速和负荷并不一定服从常规分布，而极有可能服从不规则分布。那么，基于常规分布的概率模型将致使PPF产生巨大误差。

多项式正态变换技术基于随机变量的历史数据建模，其具备处理随机变量服从任意分布且分布间存在相关性的能力[9]。九阶多项正态变换（Ninth-order Polynomial Normal Transformation，NPNT）能够计及随机变量前九阶矩信息，其所建立的概率模型具备精度高和适应性强等特点[10]。因此，文中将NPNT引入PPF计算中，用其建立输入概率模型。

建立输入概率模型是PPF的第一步，第二步则是利用概率分析方法在DPF中传递概率信息，并获取PPF结果。通常，PPF可以分为解析法、近似法和蒙特卡洛仿真法（Monte Carlo Simulation，MCS）[11-14]。解析法计算效率高，但计算精度难以令人满意[15]。近似法能较好平衡PPF计算速度和精度之间的矛盾，但其无法直接获得PPF结果的概率密度函数，导致难以对PPF计算结果深入分析[16]。MCS计算精确度高，但其极其耗时[14-16]。

拟蒙特卡罗方法（Quasi Monte Carlo，QMC）[10]不但能够兼顾计算精度和计算速度，而且具备输出PPF结果矩信息、频率直方图以及概率密度函数的能力。因此，文中将NPNT与QMC相结合，提出一种基于NPNT和QMC的概率潮流算法。该方法直接利用电网中随机变量（如风电出力）的历史数据建立概率模型，不依赖于任何人工经验及假设，进而精准模拟随机变量服从任意分布且分布间存在相关性的场景。通过与QMC相结合，所提概率潮流算法能够平衡好概率潮流计算速度和计算精度之间的矛盾，具有良好的工程实用价值。

1 概率潮流计算模型

DPF模型可以看成一个多输入多输出的隐函数：

式中：PG表示传统电源的出力；PRG表示风电出力；PLG表示负荷的值；Z表示系统的拓扑参数；V和δ表示系统的电压和功角；Pline代表线路潮流。

在DPF模型中将负荷和风电出力看成是确定性的数值，显然这无法全面反应风电和负荷的随机性对电网的影响。如果风电、负荷等输入变量当成是随机变量，那么该问题就变成概率潮流计算问题。

2 九阶多项式正态变换技术

随机变量（如风速、负荷等）受到多种因素影响，其可能不服从常规概率分布。同时，相邻地区随机变量间的相关性也不能忽视。因此，文中将引入NPNT技术处理上述问题。

2.1 NPNT中多项式系数的估计

多项式正态变换的核心思想是利用标准正态变量的多项式运算模拟服从任意分布的随机变量。九阶多项式可以表示为[10]：

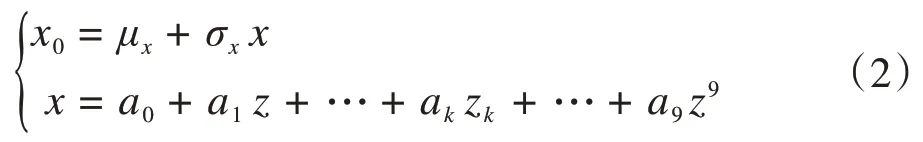
式中：x0表示实际电网中的连续型随机变量（如风速）；μx和σx分别表示输入随机变量x0的均值和标准差；x表示经标准化处理后的随机变量；z表示服从标准正态分布的随机变量；ak（k=0、1、2、…、9）为待评估的多项式系数。若能够计算出ak（k=0、1、2、…、9），那么就能通过标准正态分布模拟服从任意分布的随机变量。

数据矩通常被用于表征数据的概率特征，可以通过计算变量历史数据的数据矩估计出多项式系数。文中采用概率权重矩刻画电网中历史数据的概率特征，其计算方法如下[17]：对随机变量历史数据进行大小排序x1≤xi≤xn，进而可以推出概率权重矩计算公式。

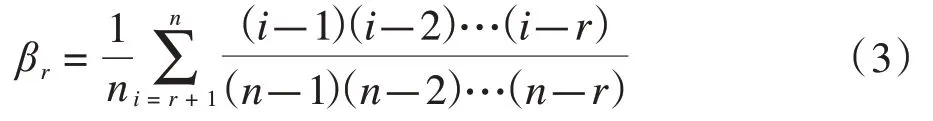
基于公式（4）和（5）可以求出九阶多项式的系数。

式中：Φ(z)和φ(z)表示标准正态分布的累积概率分布函数和概率密度函数。…、9）表示常数值，其可以由数值积分求得。注意，公式（5）是一个线性化的公式，因此九阶多项式的系数能够快速求得。

2.2 相关系数的估计

电网中相邻地区的随机变量之间具有一定的相关性，例如相邻风电场出力具有相关性。因此，概率模型不但要考虑电网中随机源的不确定性，也必须考虑随机源之间的相关性。假设x1、x2是两个服从任意分布且经标准化的随机变量，那么其可以表示为

随机变量z1、z2（服从标准正态分布）之间的相关系数ρz与随机变量x1、x2（服从任意分布）之间的相关系数ρx的函数关系可以表示为：

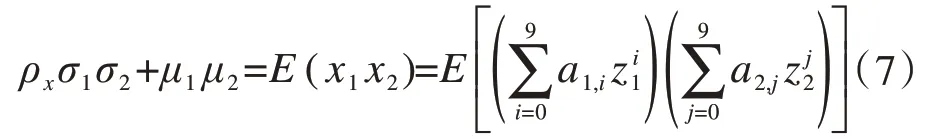
式中：μ1、μ2和σ1、σ2分别表示x1、x2的均值和标准差。表示关于ρz的多项式，详细公式见文献[10]。

一般地，能通过历史数据估计出随机变量x1、x2之间的相关系数ρx，那么采用二分法能够由公式（7）求得随机变量z1、z2之间的相关系数ρz。

3 拟蒙特卡洛法

基于NPNT建立输入概率模型是概率潮流计算的第一步，第二步则是利用概率分析方法在确定性潮流计算模型中传递概率信息，以获得电网概率分析结果。

Halton序列是拟蒙特卡洛法中最常用的低差异序列，其生成的随机样本点能够更加均匀地覆盖随机空间。相比蒙特卡洛仿真法，QMC能够以更少的样本点获取更多的概率信息，进而极大地提高概率潮流分析的效率。Halton序列的生成方法如下[10]：

设R为任意质数，则任意自然数s都存在唯一的R进制表示：

式中：对于任意整数s>0，ψR(s)∈[0,1]。

那么，{ }ψR1(s),ψR2(s),ψR3(s),…,ψRn(s)就 是Haltom序列，其中n表示数列的维数。基于Haltom序列能够在均匀分布或者标准高斯分布上生成样本点集。

4 概率潮流计算的步骤

基于NPNT和QMC的概率潮流算法计算步骤如下：

步骤1：收集电网中随机变量（风电出力、负荷等）的历史数据；

步骤2：估计出随机变量对应的多项式系数，并利用九阶多项式表示随机变量

步骤3：计算电网中随机变量历史数据的相关系数矩阵，并定义为

步骤4：计算原始随机变量对应标准正态分布空间的相关系数矩阵

步骤5：利用QMC法生成n_sample组服从标准正态分布且相互独立的随机数，其中n_sample表示电网中随机变量的个数；

步骤6：基于QMC生成的随机数生成相关系数为RZ的多维标准正态分布变量矩阵Z；

步骤7：将含相关性的多维正态分布变量Z代入对应的九阶多项式以获得具有相关性且标准化的任意分布随机变量；

步骤8：将标准化的数据去标准化，即得到具有相关性且服从任意分布的随机变量；

步骤9：将上述变量逐组输入确定性的潮流计算模型，并反复进行潮流计算；

步骤10：输出概率潮流计算结果，包括电网电压、功角以及支路潮流的矩信息、频率直方图和概率密度函数等。

基于NPNT和QMC的概率潮流算法的优势有：第一，NPNT直接基于历史数据建立概率模型，能够避免人工经验的主观性对建模准确度的影响，所建立的概率模型更加贴合实际；第二，NPNT能够获取变量历史数据的前九阶矩信息，其能够精准模拟随机变量的概率特征；第三，QMC算法在保证计算精度的前提下，能够大幅提升概率潮流的计算效率；第四，所提算法能够输出计算结果的矩信息、频率直方图等，方便电网规划运行人员全面准确地识别电网风险。

5 仿真测试

应用IEEE118节点[17]系统验证文中所提概率潮流算法的有效性。七个风电场（包括WF1、WF2、WF3、WF4、WF5、WF6和WF7）通过母线35、36、43、44、45、46和90接入系统。测试系统中风电场风速数据来源于风电场测风记录[18]。假设风电场WF1、WF2、WF3、WF4、WF5、WF6、WF7风速之间的相关系数0.3。

5.1 NPNT有效性评估

采用频率直方图相似度指标（Frequency Histogram Similarity Index，FHSI）衡量两个频率直方图的重叠程度[18]，其定义为：

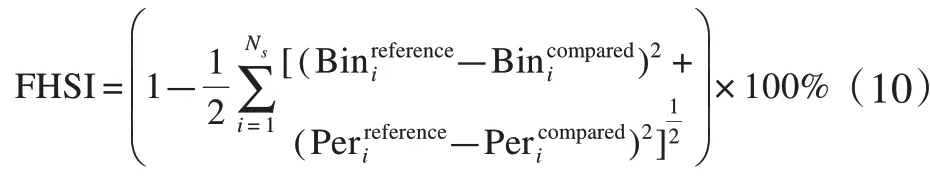
表1中给出了由NPNT、Gaussian和Weibull分布所得到频率直方图相似度指标FHSI。Gaussian和Weibull分布的FHSI的平均值分别为78.45%和82.85%。NPNT的FHSI的平均值为93.92%。事实上，NPNT的大部分FHSI指标均高于93.5%。这说明，基于NPNT的概率建模方法是准确的。因此，在概率潮流分析中NPNT将用于建立输入概率模型。

表1 NPNT、Gaussian、Weibull分布的FHSI值 %

5.2 概率潮流算法性能评估

为了验证文中所提概率潮流算法的有效性，运用基于NPNT的MCS仿真法作为参考结果，其在输入概率模型中选取50 000个样本点。为了说明不准确的概率建模将影响概率潮流计算结果，利用Weibull分布直接拟合风速数据、运用Gaussian分布拟合负荷数据，同时基于QMC法进行概率信息传递组成一种新的概率潮流算法。因此，将有如下算法参与计算，并进行性能对比：

1）参考算法：将NPNT和MCS仿真法相结合的概率潮流算法，简称NPNT-MCS；

2）文中所提算法：基于NPNT和QMC的概率潮流算法，简称NPNT-QMC；

3）对比方法：基于常规分布（Common Distributions）和QMC仿真法组成的概率潮流算法，简称CDQMC。

表2和表3给出了交流系统电压均值和标准差的相对误差。文中所提算法交流电压均值的相对误差均小于0.7%，电压标准差的相对误差均小于2.5%，具有良好的计算精度。上述计算结果充分说明了文中所提算法的有效性。

表2 交流母线电压均值相对误差 %

表3 交流母线电压标准差相对误差 %

表4给出了参考算法、NPNT-QMC和CD-QMC的计算时间分别为11 132.75 s、100.26 s、99.06 s。与参考算法对比，文中所提算法能够极大地降低概率潮流分析的计算负担，同时保持令人满意的计算精度。与对比算法CD-QMC相比，概率潮流分析所需时间相近，但是文中所提算法能够极大地提高概率分析精度。因此，文中所提算法能够在概率潮流计算速度和计算精度中达到较好地平衡。

表4 计算时间对比

6 结语

针对现有大多概率潮流算法假设电网中随机变量为常规概率分布的问题，文中提出了一种基于NPNT和QMC的概率潮流算法。该算法不但能够处理电网中随机变量服从任意分布且分布间存在相关性的问题，而且能够较好地平衡好概率潮流分析中计算速度和精度之间的矛盾。此外，所提算法能够获得概率潮流计算结果的矩信息、频率直方图和PDF信息，以便电网运行规划人员深入分析计算结果。