基于CHSH 不等式几何解释的“X”态量子非局域关联检验*
曾柏云 辜鹏宇 胡强 贾欣燕 樊代和
(西南交通大学物理科学与技术学院,成都 610031)
量子非局域关联现象是量子理论区别于经典理论的重要特征之一.“X”态作为一种典型的量子混合态,基于其进行的量子非局域关联的检验研究,不论对验证量子理论的正确性,还是在量子信息论的应用领域研究,都具有重要的意义.本文在基于传统Clauser-Horne-Shimony-Holt (CHSH)不等式进行量子非局域关联检验的基础上,提出了一种基于“X”态几何解释的量子非局域关联检验策略.利用“X”态的几何解释策略,可使物理图像更为直观地研究检验时最优化测量基选取,以及可获得的最大CHSH 不等式检验值等.最后给出了基于CHSH 不等式几何解释策略,“X”态成功进行量子非局域关联检验的参数范围.
1 引言
量子非局域关联现象最早于1935 年由Einstein等[1]引入(即所谓的EPR 佯谬现象的提出),其揭示了量子理论和经典局域实在论之间的尖锐矛盾.随着量子非局域关联现象在量子信息学中的深入研究和应用,诸如量子通信[2]和量子计算[3]等方案应运而生.可以说,量子非局域关联性是量子理论最基本的特性,也是量子信息学发展的关键[4].
为了检验量子非局域关联的存在,1964 年,Bell[5]提出了著名的Bell 不等式.在Bell 不等式的基础之上,1969 年,Clauser 等[6]发展出了一种更适于实验验证的不等式,即CHSH 不等式.CHSH不等式的经典上限为Sc-max=2,而对于量子理论,其上限可达到.因此,通过检验CHSH不等式的上限值,即可检验量子非局域关联的存在.在CHSH 不等式提出之后,相关量子非局域关联的实验检验也相 继展开.如1972 年,Freedman和Clauser[7]报道了对CHSH 不等式6 倍标准差违背的实验验证.Aspect 等[8]在1982年利用时变分析仪检验了CHSH 不等式,结果与量子力学预测一致.尽管在CHSH 不等式提出之后,CGLMP不等式[9]、Inn22不等式[10]、MABK 不等式[11-13]等量子非局域关联检验方案被相继提出,并且一些无不等式的方法,如GHZ定理[14]和Hardy 定理[15]也相继问世,但CHSH不等式仍然是用来证明量子非局域关联存在的强有力工具.在如今量子信息学的各个领域,如量子通信、量子密钥分发和量子隐态传输等也不乏利用CHSH 不等式检验量子非局域性的身影[16-18].
然而,无论是基于不等式的方法还是基于无不等式的方法,它们在进行量子非局域关联检验时,均存在物理图像不直观的问题.这种不直观性体现在,人们难以寻找最佳的测量基,并且进一步加大了量子非局域检验的计算量.针对这一问题,2021 年,Seiler 等[19]提出了一种基于CHSH 不等式的非最大纠缠态的几何解释方案.该方案使用两个Bloch 球和一个关联矩阵的组合,通过直观的图像分析,可以较为方便地找出最优的测量基策略,最终使利用CHSH 不等式的检验过程的物理图像更加直观.并且,这种图像解释不仅适用于纠缠纯态,还适用于纠缠混合态.
众所周知,由于实验过程中存在各种噪声,以及环境退相干效应对量子态制备的影响,使得实验制备的量子态通常为一混合态,所以基于混合态的量子非局域关联检验就变得尤为重要.1989 年,Werner[20]构造了一种典型的混合态(即Werner态).2002 年,Zhang 等[21]利用光子的自发参量下转换和受控退相干成功制备了Werner 态,这为实验检验基于混合态的量子非局域关联提供了可能.实际上,在量子理论中,还存在一种典型的混合态,由于该混合态密度矩阵的对角线和反对角线中非零元组成了一个“X”的形状,且在常见的噪声影响下,其演化过程仍能使密度矩阵保持为“X”型[22],因此也被称为“X”态.
事实上,这种“X”态并不罕见,它可以在各种物理环境中产生.目前,“X”态在量子信息领域中被越来越多地利用.如 Shi 等[23]利用“X”态研究了量子比特与局域退相干信道相互作用时多体纠缠的动力学演化.Namitha 和Satyanarayana[24]构造了单光子相干态和双光子相干态这两类“X”态,并将它们作为初始态来研究马尔可夫近似下的纠缠动力学等.2022 年,Mishra 等[25]研究了“X”态在马尔可夫和非马尔可夫信道中的相干性.Guo 等[26]研究了任意两比特“X”态的局域量子不确定性和几何结构的突变性等.
但是,到目前为止,一种能够较为直观或基于图形化的、基于“X”态的量子非局域关联检验方案还未见报道.尽管我们课题组在2020 年利用Hardy 定理对“X”态进行了量子非局域关联检验研究,给出了任意“X”态能够进行量子非局域关联检验的条件和范围[27],但是,该检验方案依然存在检验中物理图像不直观的问题.
基于上述原因,在文献[19]的启发下,本文从CHSH 不等式的Bloch 球描述出发,首先给出基于几何解释的策略,然后利用上述方法对 “X”态进行了基于图形化的量子非局域关联检验研究.并对得到的图像进行详细分析,给出最优化检验策略.最终给出了“X”态在不同纠缠度和不同保真度下,成功进行量子非局域关联的条件和范围.
2 基于“X”态的CHSH 不等式几何解释方法
考虑一 “X”态作为研究对象,其密度矩阵可以写为[22]
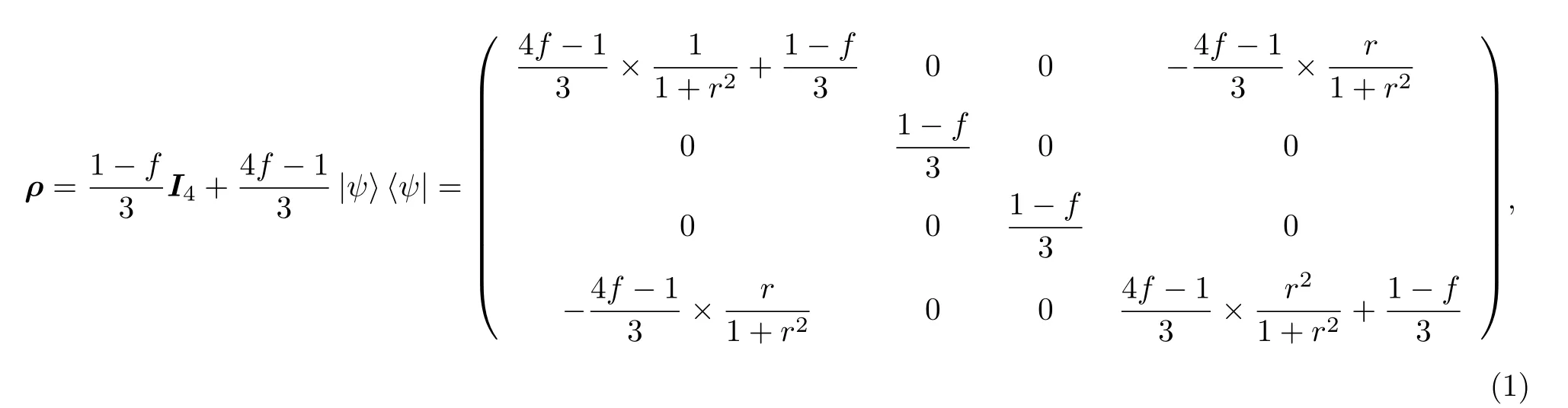
对(1)式所示的“X”态进行量子非局域关联检验时,关于CHSH 几何解释的最优化测量基问题,可归为研究一个椭球与一个截面相交的椭圆内接平行四边形的周长问题.如对“X”态的两个子系统,可分别进行两种测量: 在A(B)系统中,可用Q=q·σA(P=p·σB),J=j·σA(T=t·σB)两个算符来表示相应的测量.其中,q(p)和j(t)分别表示A(B)系统中的两个测量向量,表示A(B)系统中两个测量基的选取方向.σA(σB)表示泡利算符,可以是σx,σy,σz中的任意一个.
根据CHSH 不等式[6],可以将(2)式所示的S期望值的大小与经典理论上限Sc-max=2 做比较,当S>Sc-max时,即可说明“X”态能够被成功用于基于CHSH 不等式的量子非局域关联检验.
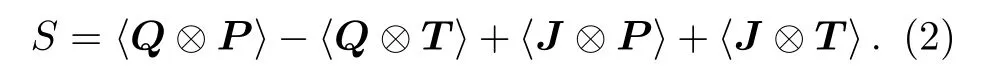
将上述对A,B 系统的测量算符分别代入到(2)式,通过计算可进一步得到CHSH 不等式中的S表达式为

实际上,上述理论分析可用图1 所示的两个Bloch 球来进行几何分析.即可用A,B 系统的两个Bloch 球中,选取4 个测量方向(即j,q,p和t)和它们的关联矩阵K来描述(3)式所示的期望值S.
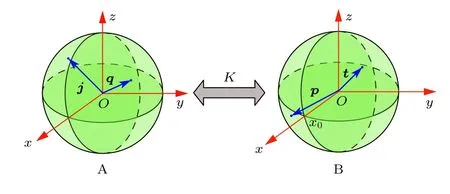
图1 基 于CHSH 不等式 的Bloch 球表示 图.左右两 个Bloch 球分别代表A 和B 两个系统,它们之间的关系由一个关联矩阵K 进行描述. j 和 q 表示A 系统中的两个测量方向,p 和 t 表示B 系统中的两个测量方向Fig.1.Diagram of Bloch ball representation based on CHSH inequality.The left and right Bloch sphere represents the two sub-system A and B,respectively.The relationship between them is described by a correlation matrix K.j and q represents the two measurement directions in system A,p and t represents the two measurement directions in system B.
根据泡利算符的具体表达式,并将(1)式代入kmn的表达式中,即可计算得到“X”态A,B 两个子系统之间的关联矩阵K的矩阵元素为

在考虑上述等效操作后,(3)式可以进一步写为
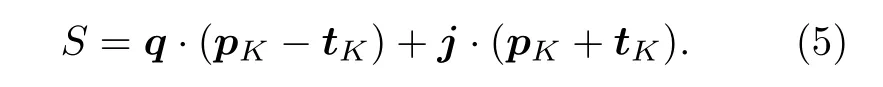
为了能够获得最大的S值,接下来用几何方法,对(5)式的结果做进一步分析.在实际的量子非局域关联检验过程中,由于A,B 两个子系统中的4 个向量(即j和q,p和t,分别表示了选取的测量基)可任意选取,因此可以通过选取最优化的向量方向来获取(5)式的最大值.如考虑到向量q和j分别是子系统A 中的单位向量,因此可以选取向量pK -tK(pK+tK)和向量q(j)的方向相同,即可将(5)式中的向量点乘关系,最大化地约化到仅与向量模大小运算相关的表达式:
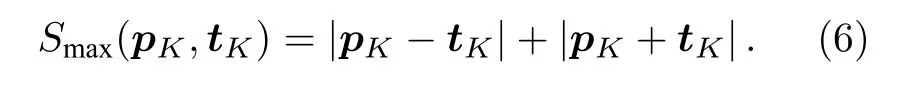
为了能够进一步得到 (6)式的最大值,可以将图2 所示的Bloch 球进一步简化到一个椭圆平面进行研究.如图2 中,选取过B 系统椭球的球心O,且包含向量pK和tK构成的平面,与Bloch 椭球相交,得到一个新椭圆平面.并以O为坐标原点,建立新的二维坐标系x′-y′,如图3(a)所示.其中x′轴处于椭圆短轴方向,y′轴处于椭圆的长轴方向.

图2 将关联矩阵K 作用于B 系统后的Bloch 球表 示图.其中A 系统的Bloch 球保持不变,B 系统的Bloch 球受关联矩阵K 的影响而发生改变.两系统间的关联由单位矩阵I 来描述Fig.2.The Bloch sphere representation diagram by applying the correlation matrix K to system B.The Bloch sphere of system A keep constant.The Bloch sphere of system B is changed.The correlation between two systems is described by the unit matrix I.

图3 B 系统Bloch 球退变为一椭圆平面时的表示图 (a)向量 p K 在椭圆上的交点 为 B 1,向 量 t K 在椭圆上 的交点 是B2,红色虚线表示向量 p K +tK,橙色点划线表示向量pK -tK ;(b) 向量 p K 在椭圆上的 交点是 C 2,向 量 t K 在椭圆上的交点是 C 3,橙色点划线表示最大期望值SmaxFig.3.Diagram of elliptic plane when the Bloch sphere of system B is changed: (a) The intersection of vector p K on the ellipse is B 1,the intersection of vector t K on the ellipse is B 2 .The red dashed line indicates vector p K+tK,and the orange dotted line indicates vector p K -tK .(b) The intersection of vector p K on the ellipse is C 2,and the intersection of vector t K on the ellipse is C 3 .The orange dotted line indicates the maximum expectation value of Smax .
此时,在图3(a)中,通过将向量pK -tK和pK+tK分别平移到的B3B4和B2B3位置,即可在椭圆平面内构成一平行四边形B1B2B3B4.在这种情况下,B1B2的长度 将等于向量|pK -tK|,且B1B4的长度将等于|pK+tK|.而最大量子非局域关联检验结果的研究,将变为如何通过选取最优化的向量pK,tK,使平行四边形B1B2B3B4周长实现最大化的几何问题.
结合上述分析得到的图2 中B 系统Bloch 球x,y,z轴长度不同的特点,再结合几何关系分析[29]可以得出,当tK选取为沿x轴方向,pK选取为沿z轴方向时,平行四边形B1B2B3B4将变为图3(b)所示的菱形C1C2C3C4,此时,将获得|pK -tK|+|pK+tK|的最大值,也即获得CHSH不等式S的最大值.
根据图3(b)的几何图形关系,就可以非常方便地计算得到“X”态基于CHSH 不等式的最大化量子非局域关联检验的结果为

此时,只需判断Smax>2 是否成立,即可说明 “X”态能否进行基于CHSH 不等式的量子非局域关联检验研究.同时,进行量子非局域关联检验时的最优化测量基的选取方式也可以确定: 即选取B 系统的两个测量方向p和t分别沿着Bloch 球的z轴方向和x轴方向,且进一步选取A 系统中的两个测量方 向q和j,分别满 足即可.
3 “X”态量子非局域关联检验结果分析
利用几何分析方法得到的最大CHSH 不等式检验结果(7)式(即选取最优化的测量基时),选取3 个 特定的保真度值(即f=0.78,f=0.90 以及f=1),可以得到如(1)式所示的“X”态,进行量子非局域关联检验时,Smax随r的变化关系曲线如图4 所示.

图4 在不同保真度f 下,S max 随r 的变化关系图Fig.4.Plot of S max vs. r under different values of fidelity f.
从图4 可以看出,当f=1 (图中红色圆点表示,此时“X”态约化为一偏振纠缠纯态)且取最优化测量基的情况下,只要r>0,“X”态均可进行基于CHSH 不等式的量子非局域关联检验(即Smax>2 ).且随着r值的增大,Smax的值也非线性地增大.特别地,当r=1时(最大纠缠态),可获得该结果与Clauser 等[6]的研究结果完全一致,证明了本文得到的基于几何解释的正确性.
当f=0.78 (图4 中黑色实心框表示)且取最优化测量基的情况下,无论r为何值,均将得到Smax≤2,说明此时的“X”态不能进行基于CHSH不等式的量子非局域关联检验.而当保真度的取值位于 0.78<f <1 时,仅有部分“X”态可成功用于基于CHSH 不等式的量子非局域关联检验研究.
同理,图5 给出了在3 个特定r值(即r=0,r=0.50 以及r=1)下,且选取最优化测量基时,Smax随保真度f的变化关系曲线.
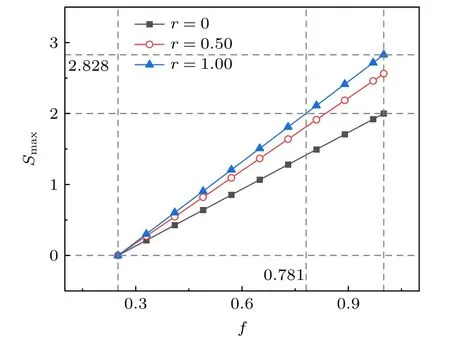
图5 在不同r 下,S max 随保真度f 的变化关系图Fig.5.Plot of S max vs. fidelity f under different values of r.
从图5 可以看出,不论r取何值,随着保真度f的增大,Smax均将线性地增大.并且随着r值的增大,可用于成功检验量子非局域关联检验(即Smax>2)的f值的范围也将增大.为了能够清晰地表示在不同r取值范围下,“X”态能够成功进行基于CHSH 不等式的量子非局域关联检验的保真度范围,给出了fmin随r的变化关系曲线,如图6 所示.
从图6 可以看出,随着r的增大,fmin的值将非线性地减小,这也意味着可用于进行量子非局域关联检验的“X”态的范围将非线性地增大.特别地,当(1)式所示的“X”态中|ψ〉为一最大偏振纠缠态时(即r=1),可用于进行量子非局域关联检验的“X”态的范围最大,即只要保真度f>0.781 即可.
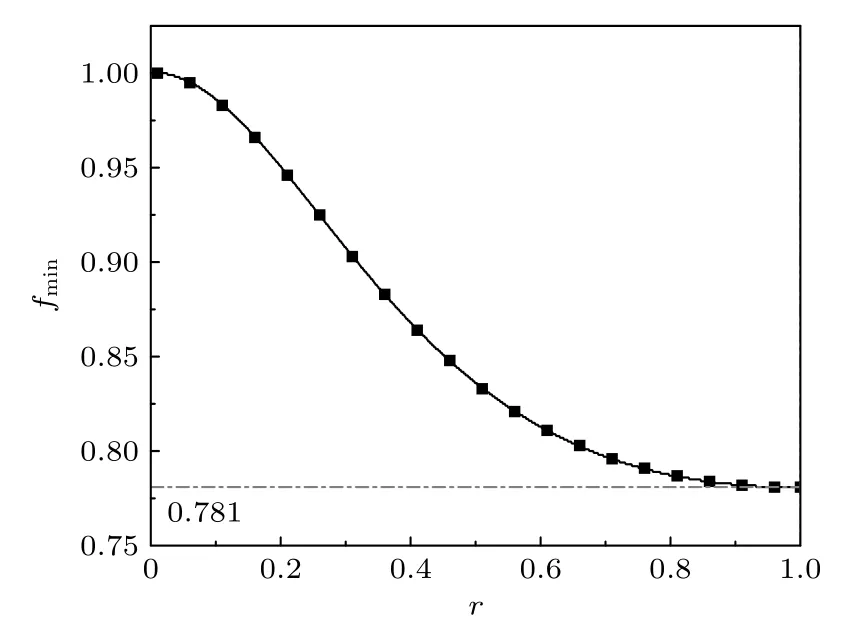
图6 f min 随r 的变化关系图Fig.6.Plot of f min vs. r.
为了更加全面地描述“X”态在不同保真度f以及r取值时的量子非局域关联检验情况,图7 给出了(1)式所示的“X”态进行量子非局域关联检验时的最大期望值Smax随f和r的变化关系.从图7 可以看出,Smax的值随f和r值的增大均呈现出连续变化的现象.只有在满足一定条件时,“X”态才能够成功地(即Smax>2)进行基于CHSH 不等式的量子非局域关联检验研究.进一步,从图7 可以看出,不论r取何值,Smax随保真度f值的变化,基本呈现线性变化关系;而不论保真度f取何值,Smax随r值的变化均呈现出非线性变化关系.

图7 S max 随保真度f 和r 的变化关系图Fig.7.Plot of S max vs. fidelity f and r.
4 总结
在传统基于CHSH 不等式进行量子非局域关联检验研究的基础之上,本文提出了一种以量子“X”态作为研究对象的几何解释策略.从“X”态的Bloch 球分析研究出发,利用几何解释的方法,分别给出了“X”态进行基于CHSH 不等式的量子非局域关联检验研究时,最优化测量基的选取策略,以及可获得的最大CHSH 不等式检验值.这种几何解释的方法,可进一步降低进行量子非局域关联检验时的理论计算量,同时也可使量子非局域关联检验的物理图像更为直观.
通过几何解释研究发现,当“X”态的保真度f=1时,由于“X”态将直接约化到一偏振纠缠纯态,对其进行的量子非局域关联检验结果与传统的基于CHSH 不等式进行检验的结果完全一致(最大CHSH不等式值为),证明了本文提出的几何解释方案的正确性.而当f<1 时,仅有部分“X”态(即r值存在一定范围)可成功用于量子非局域关联的检验研究.同时,研究还发现,随着r值的增大,可进一步扩大可成功进行量子非局域关联检验的保真度f值的范围.特别地,当r=1时,保真度f取值范围最大,即只要满足f>0.781,该“X”态即可成功用于基于CHSH 不等式的量子非局域关联检验研究.
实际上,本文的研究结果在基于“X”态进行的量子非局域关联实验检验方面也具有一定的指导价值.如可通过密度矩阵的重构操作,首先得出制备的“X”态的密度矩阵具体表达式,并进一步分析得到该“X”态的保真度f以及r参数值.而本文的研究结果,已经较为清晰地给出了在特定f和r值的情况下,该“X”态能否成功进行量子非局域关联的实验检验研究.如能够满足检验要求,则可进一步选取本文基于几何解释得出的最优化测量基,进行实际的实验检验.
本文提出的几何解释方案,实际上为量子态进行量子非局域关联检验的研究提供了一个物理图像较为直观的研究策略.相信本文的研究将对后续开展基于其他方案的量子非局域关联检验研究提供参考.

