基于量子随机行走和多维混沌的三维图像加密算法*

刘瀚扬 华南 王一诺 梁俊卿 马鸿洋†

1) (青岛理工大学信息与控制工程学院,青岛 266520)

2) (青岛理工大学理学院,青岛 266520)

随着互联网的发展,人们对于信息安全的需求日益增加,而经典的加密技术存在着密钥空间小、易破解的缺陷,图像加密技术在保护图像信息安全和隐私内容等方面的问题亟待解决.量子随机行走作为一种新型量子密钥生成器,其密钥空间大,与经典随机行走相比计算速度与安全性有着明显的提高.本文提出一种基于量子随机行走并涉及Lorenz 和Rossler 多维混沌的三维图像加密算法.首先应用高斯金字塔对图像进行处理然后按照一定比例将处理后的图像切割成4 份;其次使用量子随机行走生成的随机序列与多维混沌中的Lorenz 混沌系统生成的随机序列对分成的若干块子图像进行汉明距离计算然后进行合成,并且对图像RGB三通道之间进行欧氏距离计算;最后将汉明距离与欧式距离取余得到的序列值作为初始值输入多维混沌中的Rossler 系统,生成随机序列作为密钥对图像的RGB 通道进行异或操作得到加密后的图像,对应解密方案为加密过程逆过程.此外,本文采用基于离散余弦变换和奇异值分解的盲水印嵌入算法将水印信息嵌入到加密后的图像中,实现接收方可以通过提取水印,根据水印信息的完整性来判断传输过程中图像是否遭受到攻击破坏,如无遭受恶意攻击,则对图像进行解密操作.这一操作完善了对图像信息安全的保护.实验结果表明加密后图像的峰值信噪比稳定在7—9 之间加密效果较好,灰度差评分接近1,加密图像的相关性均匀分布,其相关性系数接近0,密钥空间2128 且加密后的直方图分布均匀,具有较高的抵御统计分析攻击的能力.

1 引言

随着互联网的普及,暴露在公共网络通信中的文字、音频、图像、视频等易受到第三方恶意攻击和窃听,因此通过加密数字图像保护图像信息安全和隐私内容显得极为重要.

量子密码学[1-4]作为经典密码与量子力学原理相结合的产物在加密通信等方面有着巨大的作用.在过去的几十年里,经典的随机行走和马尔可夫链被用作发展计算机科学和数学算法的框架.量子力学原理与经典的随机行走相结合,提供了一种新的模式,即量子随机行走.1687 年,Aharonov 等[5]最早提出了一维量子随机行走,利用量子态相干性使得量子随机行走比经典随机行走扩散速度更快.随着研究的发展,Farhi 和Gutmann[6]于1998 年提出了连续时间量子随机行走的概念,在量子随机行走的研究道路上起着重要的作用;Childs 等[7]于2003 年提出了一种连续时间的量子随机行走算法.量子随机行走算法被证明相比于经典算法具有指数级的速度[8,9]和更高的安全性[10,11].2001 年,Watrous[12]将经典随机行走量子化,得到了离散时间量子随机行走的概念.从此,量子随机行走的概念被细分为连续时间量子随机行走和离散时间量子随机行走.其中,离散时间量子随机行走具有不确定性,被广泛应用于量子及经典密码学中[13-19].Gods 和Zhan[20]在2019 年以组合方法构建的三个离散时间量子行走模型和2021 年Singh 等[21]进行的离散时间量子游走的通用量子计算为本文提供了思想基础,Tsafack 等[22]于2020 年发表的基于量子随机行走的光学图像加密算法和2021 年王一诺等[23]发表的基于DNA 编码与交替量子随机行走的彩色图像加密算法给本文提供了重要的研究方向.本文采用量子随机行走算法来产生随机序列,与混沌模型相结合,整合出新的混合的随机密钥串,提高加密安全性.

混沌系统[24]具有较难预测性、初始值敏感性等特性,在密码学领域得到了极大的应用[25-28].利用混沌系统产生的随机序列对二进制的数据流图像信息进行加密,具有抗攻击能力强、安全性高的特点.Assad 和Farajallah[29]提出利用混沌伪随机数生成器在加密或解密图像过程中产生稳健的较长的一串离散值序列,进而控制参数的变化,Wang等[30]提出一个以幂指数函数和模运算的结构集成的混沌系统,针对彩色图像的三通道RGB 分量中的像素位置置乱达到加密效果.Kumar 等[31]提出利用DNA密码规则将图像的RGB 通道中的像素值转换为DNA 序列.在像素层面上使用Lorenz-Rossler 混沌系统对新生成的DNA 序列行扩散操作,在bit 层面上二维(2D) logistic 映射用于在混淆阶段对扩散后的RGB 通道执行按位混沌马尾处理,Huang 等[32]利用Rolsser 超混沌系统生成扰乱和扩散矩阵,提出一种基于Rossler 超混沌和压缩感知技术的双图像压缩-加密算法.Rakesh 等[33]利用混沌系统的混淆和扩散特点,在图像加密算法中表现出良好的性能.Huang 和Ye[34]利用置换扩散的经典结构和双二维混沌系统,设计了一种高效的自适应混沌图像加密算法模型,有效地抵抗选择明文和已知明文攻击,具有较高的安全性.Wang 等[35]通过随机密钥对混沌系统的初始值和控制参数进行初始化,SHA-512 算法对图像像素点的坐标进行置换,使加密后的图像与原始图像产生混淆关系,设计了一个基于分割的图像排列策略和一个包含三个模型的有效图像扩散策略方案,通过仿真实验,验证该算法的鲁棒性和对蛮力攻击、统计分析攻击、明文攻击、差分攻击的有效性.Zhou 等[36]通过SHA-512 哈希函数和随机小数点序列生成与明文相关的密钥流,以及基于ncc 的位级图像混淆和扩散操作,增加了密钥空间和动态密码特性,提出的新型图像加密的组合混沌系统具有良好的混沌特性和安全性.

2 相关工作

2.1 量子随机行走

量子随机行走作为一种新型的密钥生成器,密钥空间大,量子随机行走拥有优于经典的特性,其携带信息的量子态的扩散速度与经典相比有二次方的增长.

量子随机行走主要由硬币空间HwC和行走者的位置空间HwP组成,因此量子随机行走的作用空间为H=HwC⊗HwP.量子随机行走的过程分为两步,第一步是硬币算子作用在二维希尔伯特空间HwC的硬币态上,之后把酉算子作用在量子随机行走的希尔伯特空间H上,行走者根据硬币态的状态进行下一步行走.假定量子随机行走硬币算符始终选择相同的算符:

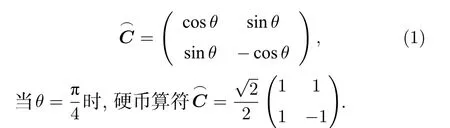
转移算符R在量子随机行走中的作用是根据硬币态的状态决定行走者下一步行走的方向.当硬币态为|0〉时,行走者将向某一方向前进一步;当状态为|1〉时,行走者将向反方向前进一步,转移算符R可以表示为

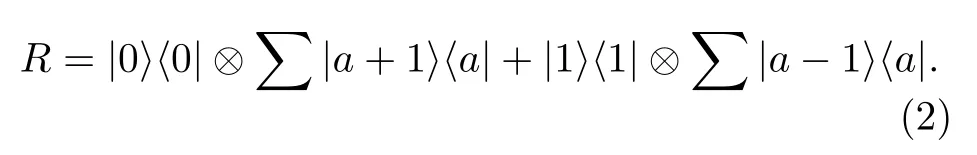
一维空间的量子随机行走的每一步操作都可以用全局U来表示:

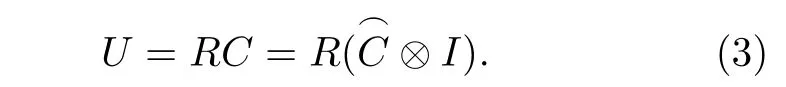
在交替量子随机行走中HwP是由位置态{|x,y〉,x,y ∈Z}张量而成,在二维空间内两个方向交替行走.因此在量子随机行走过程中,反复作用于量子随机行走系统的酉算子可以表示为

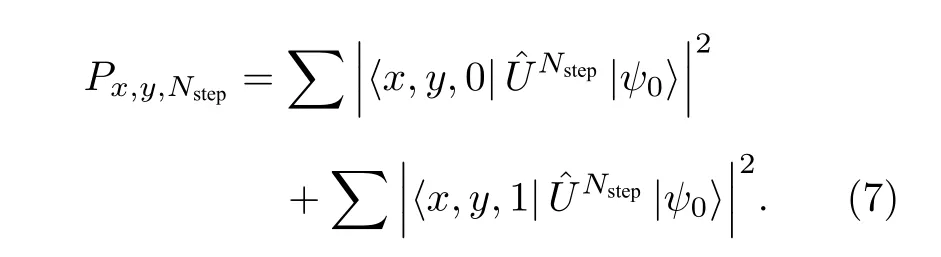
2.2 Rossler 混沌模型

相比低维的混沌模型,Rossler 结构更为复杂,抵御攻击能力更强,具有一个非线性项,可以由含参数的三维(3D)非线性常微分方程组组成,其具体形式为

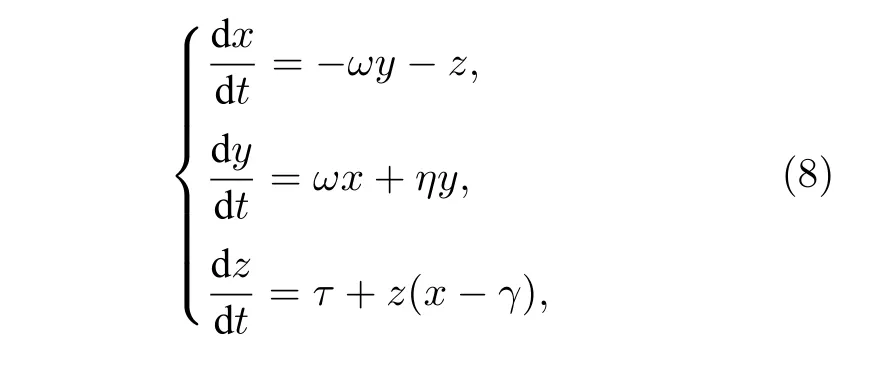
其中,ω,η,τ,γ为系统的参数.本文称ω为自然频率,是表征系统在没有外界干扰时转动快慢的量,如图2 所示.

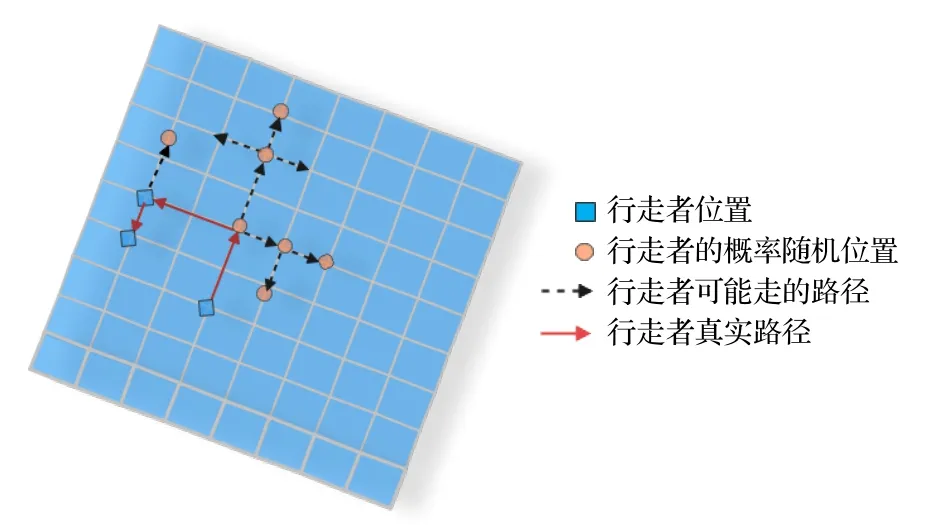
图1 量子随机行走Fig.1.Quantum random walk.

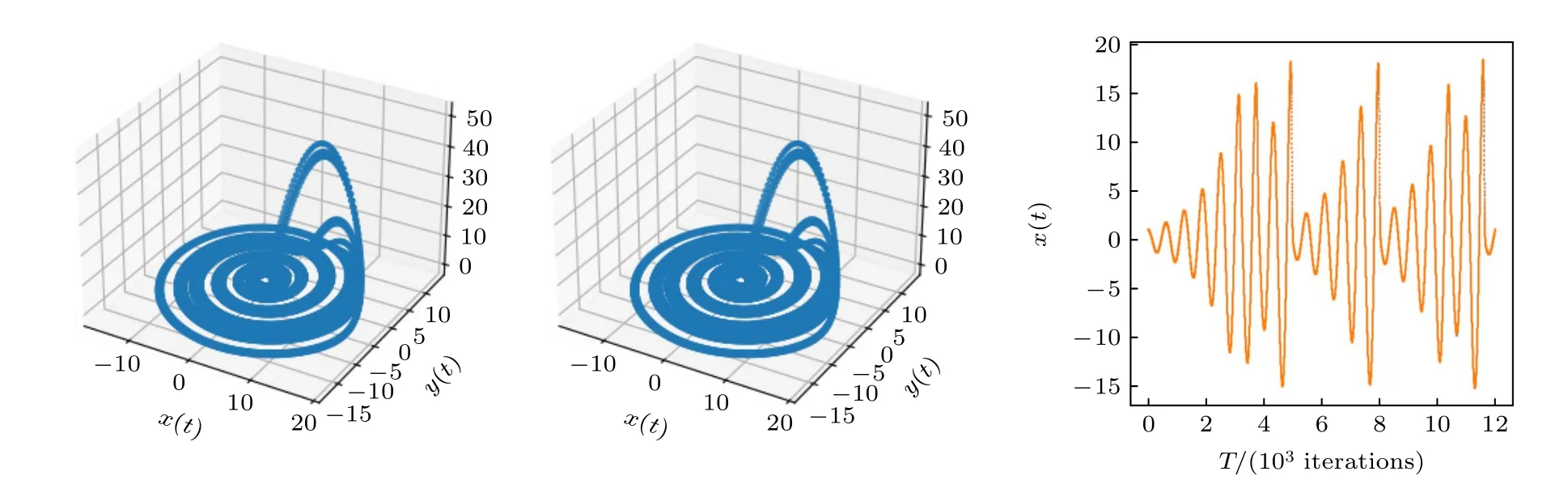
图2 Rossler 混沌模型Fig.2.Rossler chaotic model.

Rossler 振子在混沌动力学中也是研究比较多的一个模型.但用单一的混沌模型生成的随机序列来对图像加密易被破解,抗攻击性能差.

2.3 Lorenz 混沌模型

Lorenz 混沌模型也可以由三个含参数的非线性常微分方程组组成,其形式为:

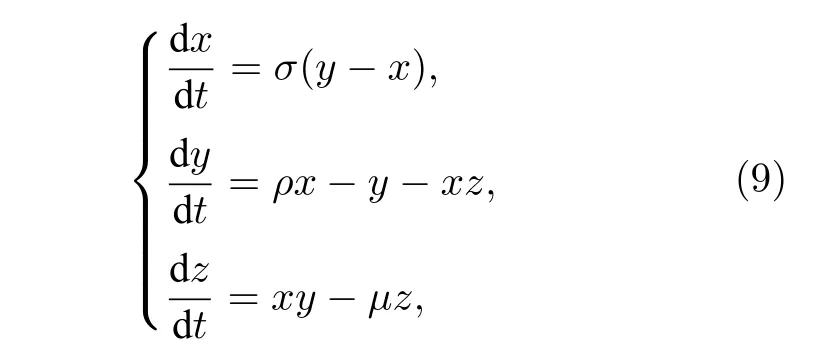
其中 三个参数分别为普朗特数σ,瑞利数ρ,方向比µ,如图3 所示.

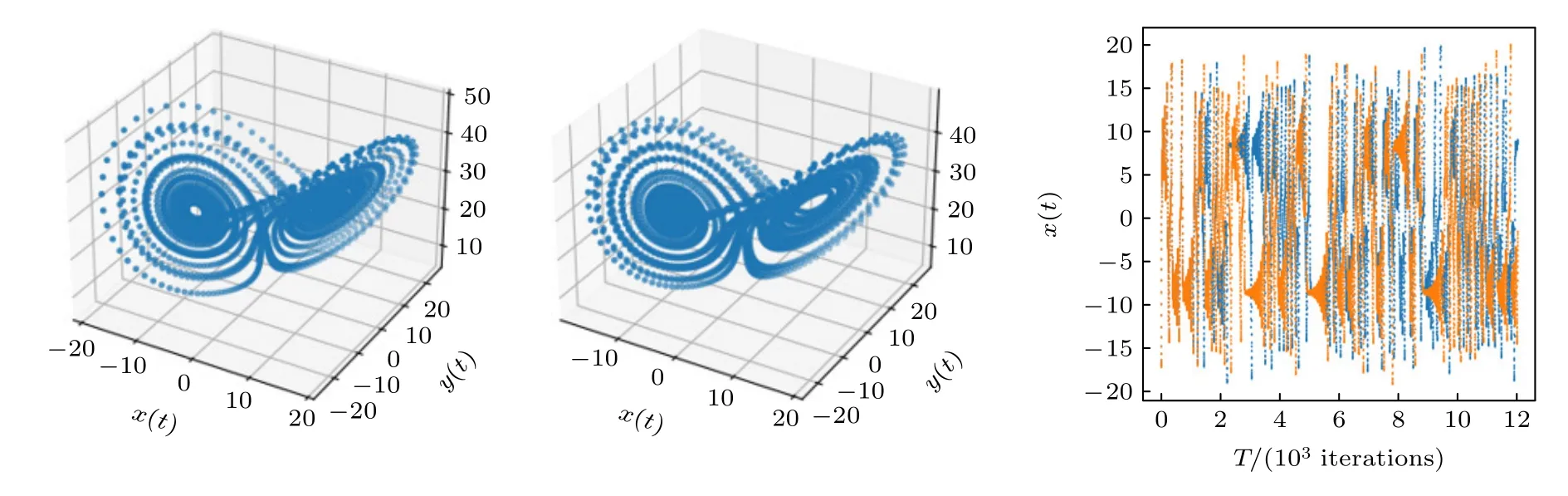
图3 Lorenz 混沌模型Fig.3.Lorenz chaotic model.

3 算法流程

基于上述Lorenz 和Rossler 混沌模型及量子随机行走的理论,得出基于量子随机行走和多维混沌的三维图像加密算法的流程分为7 个步骤: 图像分割,概率矩阵的生成与转化,Arnold 置乱,利用欧式距离与汉明距离求序列,密钥的生成,以及传输过程中的盲水印的嵌入和提取.

3.1 图像分割

高斯金字塔是为了以多分辨率来解释图像而诞生的一种简单有效的方法.本文采用高斯金字塔进行图像分割,作为加密步骤前的处理工作,将处理后的图像按照一定比例切割成若干份,分块加密与整体加密相比提升了图像的安全性能.高斯金字塔主要分成两个步骤: 第一步对图像做低通滤波,达到平滑效果;第二步对得到的平滑帧图,做下抽样,即可获得一系列的缩小的图像.将这些图像组合在一起,构造出高斯金字塔.

高斯金字塔是通过对一张图采用逐级下采样来获得的.最下层是原始图片,越往上图的尺寸越小,如图4 所示.

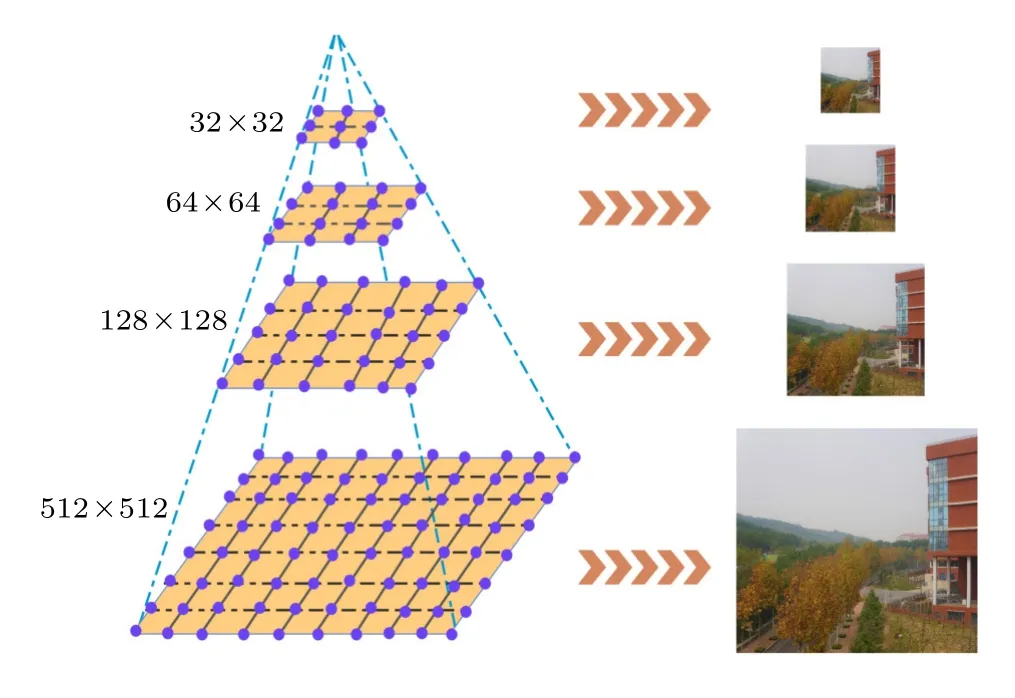
图4 高斯金字塔结构图Fig.4.Gaussian pyramid structure.

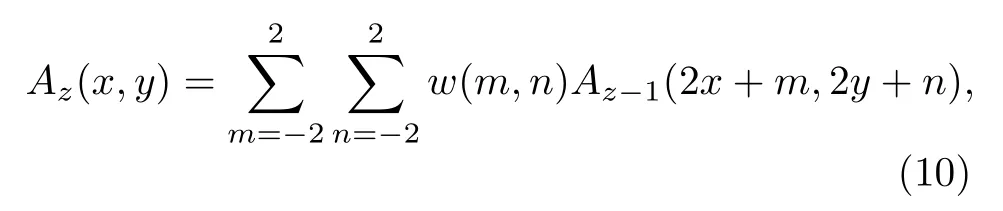
其中Az(x,y) 为第z层高斯金字塔图像;A0为原始图像;A1,···,Az表示高斯金字塔的第一层到第z层.w(m,n)=h(m)h(n) 是有低通特性的窗口函数,其中h为高斯密度分布函数.

3.2 概率矩阵的生成与转化

根据上述量子随机行走理论,设定最适合的参数(Nstep,P,λ1,λ2),得到二维量子随机行走生成概率分布P.

3.3 Arnold 置乱

二维Arnold 变换因其变换简单、有周期性的特点常被用来进行置乱图像操作,本文首先对彩色图像的三通道进行分离,然后针对分离后的三通道灰度图的各个像素点做x轴方向的错位切换,再做y轴方向的错位切换,并按照(14)式进行模运算,达到图像置乱的效果.Arnold 映射方程为

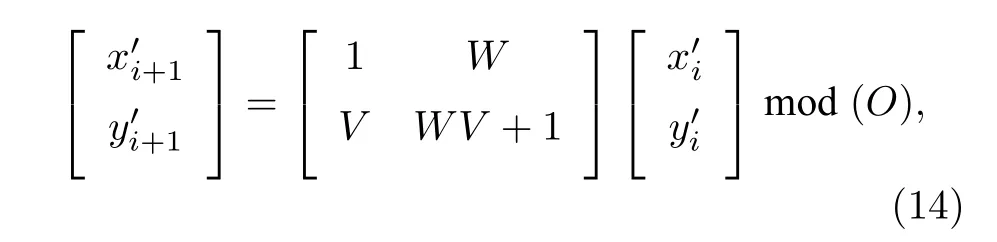
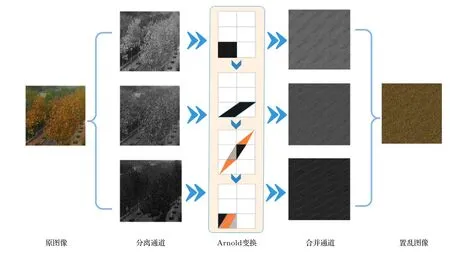
图5 Arnold 变换Fig.5.Arnold transform.

3.4 利用欧式距离与汉明距离求序列

欧式距离是衡量多维空间中两个点之间的绝对距离的常见度量方式.将序列α=(α1,α2,···,αn)看 作n维空间 点α,将β=(β1,β2,···,βn) 看 作n维空间点β,根据n维空间的欧式距离得到α与β的欧式距离并对得到的欧式距离让其结果在(0—255)之间:

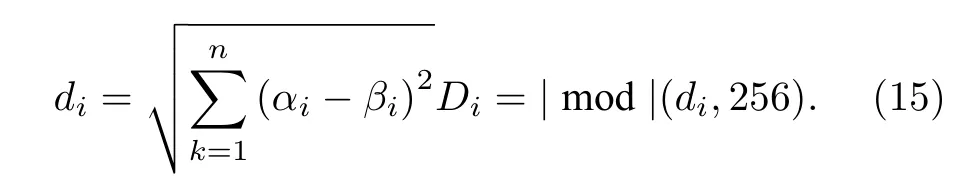
基于(15)式得到R,G,B 三通道的欧式距离DRG,DRB,DGB,

利用Lorenz 混沌模型,设定适当参数和初始值生成随机序列q=Q1,Q2,Q3,···,Qg.

将3.2 节概率矩阵的生成与转化中得到量子随机行走生成的随机序列m与Lorenz 混沌系统生成的混沌序列q的长度进行比较,即

基于汉明距离公式和上述判断公式将步骤二中得到量子随机行走生成密钥和Lorenz 混沌模型生成的密钥进行汉明距离求值得到:

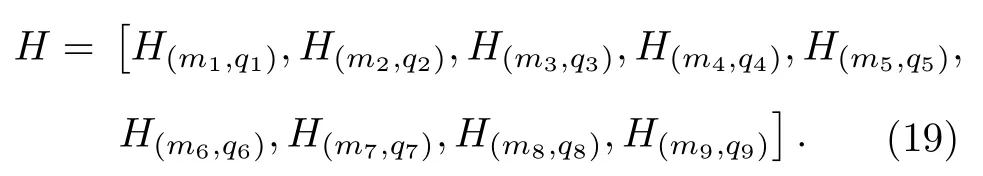
3.5 密钥的生成

将3.4 节利用欧式距离与汉明距离求序列中得到的汉明距离H与欧式距离D取余,即

其中,si是来自两个混沌系统的混沌序列.然后对原始图像进行Arnold 变换来进行置乱;最后将得到的随机序列与置乱后的图像进行异或操作进行加密和解密,如图6 所示.

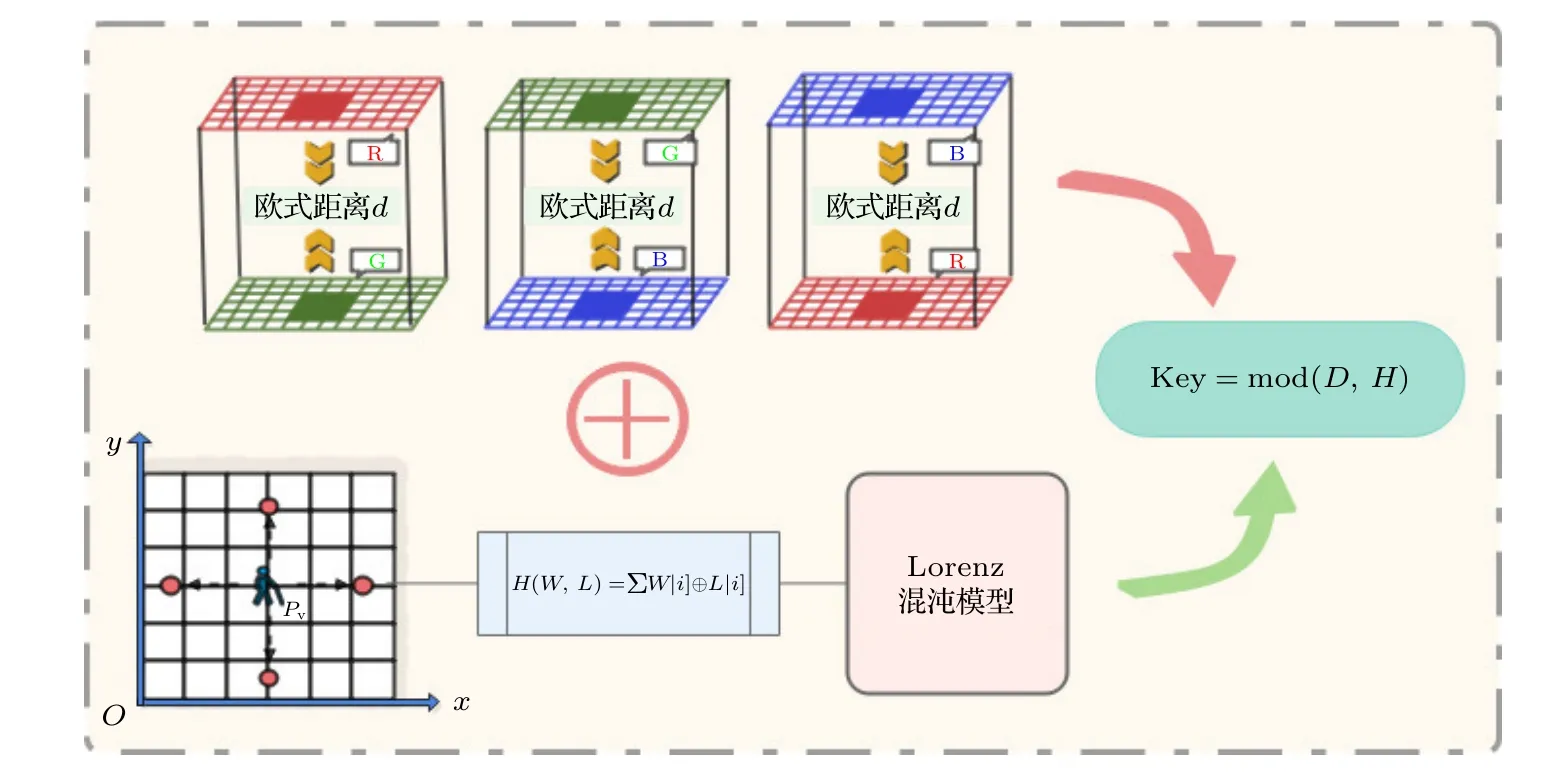
图6 密钥生成Fig.6.Key generation.

3.6 盲水印的嵌入

离散余弦变换(discrete cosine transform,DCT)将图像空间表达式从空域转换为频域,对原始图像进行DCT 变换后,生成互不相关的变换系数矩阵,明文图像的主要能量压缩到部分低频系数中去(即DCT 矩阵的左上角),使图像具有压缩比高、误码率小、信息集中等优点.二维DCT 变换如下:

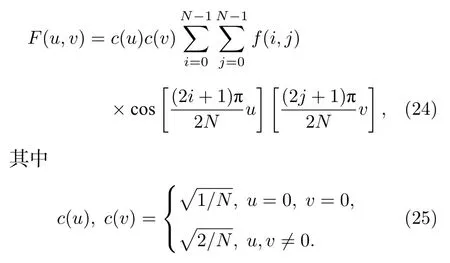
在传输过程中,盲水印算法在保护图像版权和防伪防篡改方面具有重要的作用.本文选取混沌加密后的彩色图片作为载体图片,将64 × 64 的二维码图片作为水印信息,按照DCT 变换和奇异值分解(singular balue decomposition,SVD)两个过程进行嵌入和提取,如图7 所示.

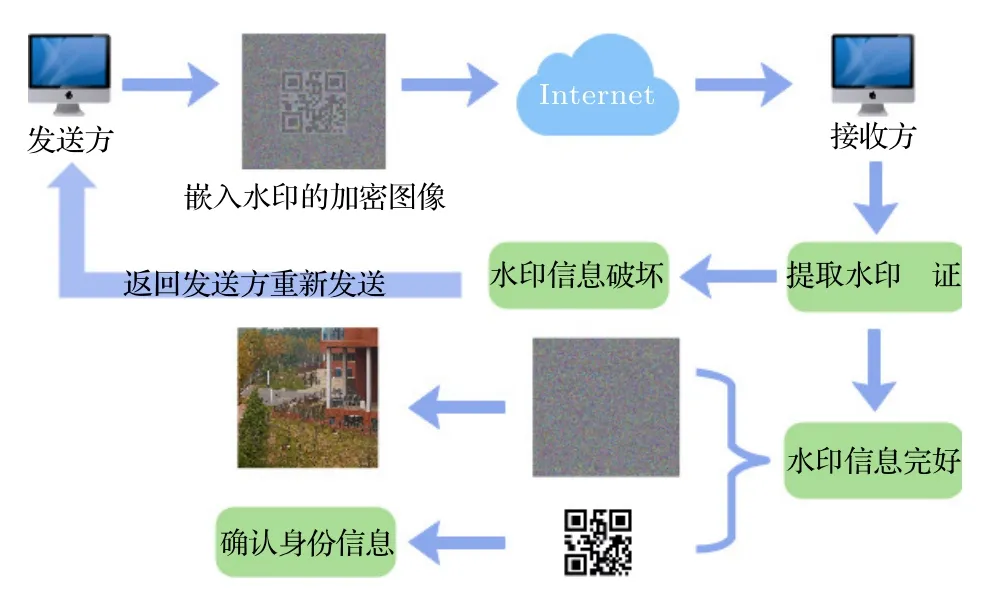
图7 水印嵌入与提取Fig.7.Watermark embedding and extraction.

首先对得到混沌加密后的图像进行读取,作为载体图像(G),将RGB 转换为YUV 格式的图像数据表示,并实现三通道分离,然后将图像分成互不重叠的8 × 8 小分块,如果图像整体长宽大小不是偶数,则扩充边缘,设置边框,添加的边界框像素值0,也就是补上白边.对每一个小分块做二维DCT变换,得到分块的DCT 系数矩阵Bij(i,j=0,1,2,···,N),其左上方为低频数据的大数值(称为直流分量),右下方为高频数据的小数值(称为交流分量),按照ZigZag 排序,取出变换后每一块矩阵的低频系数Bij(0,0) .然后对每一块Bij(0,0) 构成的矩阵Array 进行奇异值分解,得到 Array=USVT.其中,U为左正交矩阵,V为右正交矩阵,S为对角矩阵.为实现盲提取,即无需再提取图像的参数就可提取水印,本文采用求模量化方式将二值水印图像(W) 嵌入到低频系数的奇异值矩阵中.通过以下嵌入公式:

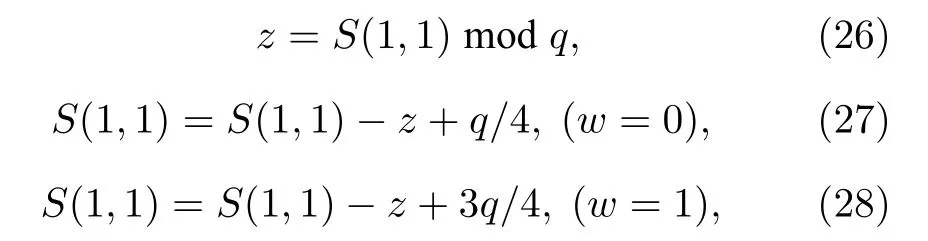
其中q代表数字水印嵌入强度,此时得到新的S1矩阵,然后利用SVD 反变换得到 Array′=US1VT,把 Array′中相应的元 素替换为Bij里的低频 系数,根据公式(24)做逆DCT 变换,就得到了嵌入水印信息W的合成图像G′.此时的水印较好地实现了不可见性.

3.7 盲水印的提取

接收方收到发送方的图像后首先进行水印提取,以验证图像在传输过程中有无受到攻击,对图像G依旧分割为8 × 8 的小块做DCT 变换,取出每块中的低频系数矩阵 Array*,对其做SVD 变换得到对 角矩阵S*=U*S*VT*,根据嵌 入公式(26)—(28)式可以得出,此时嵌入后的图像矩阵D=U1S*,将S*(1,1) 与嵌入系数q相比,若大于q/2 则提取水印矩阵W*=1,否则W*=0,最后得到可能发生变化的水印图像,然后分离出原始水印和载体图像.

4 实验仿真与性能分析

4.1 实验结果

实验测试来自作者相机拍摄的校园真实图像.图像像素大小为2048 × 2048,分割为4 幅像素大小为512 × 512 的图像,量子随机行走选取(Nstep,P,λ1,λ2)=(400,512,π /2,π /6),Lorenz 混 沌模型设定参数 (x0,y0,z0,σ,ρ,µ,T) 为(—16,—20,36,10,29,9/4,8000),加密-水印流程如图8 所示,加密仿真结果如图9 所示,加密算法如图10 所示.

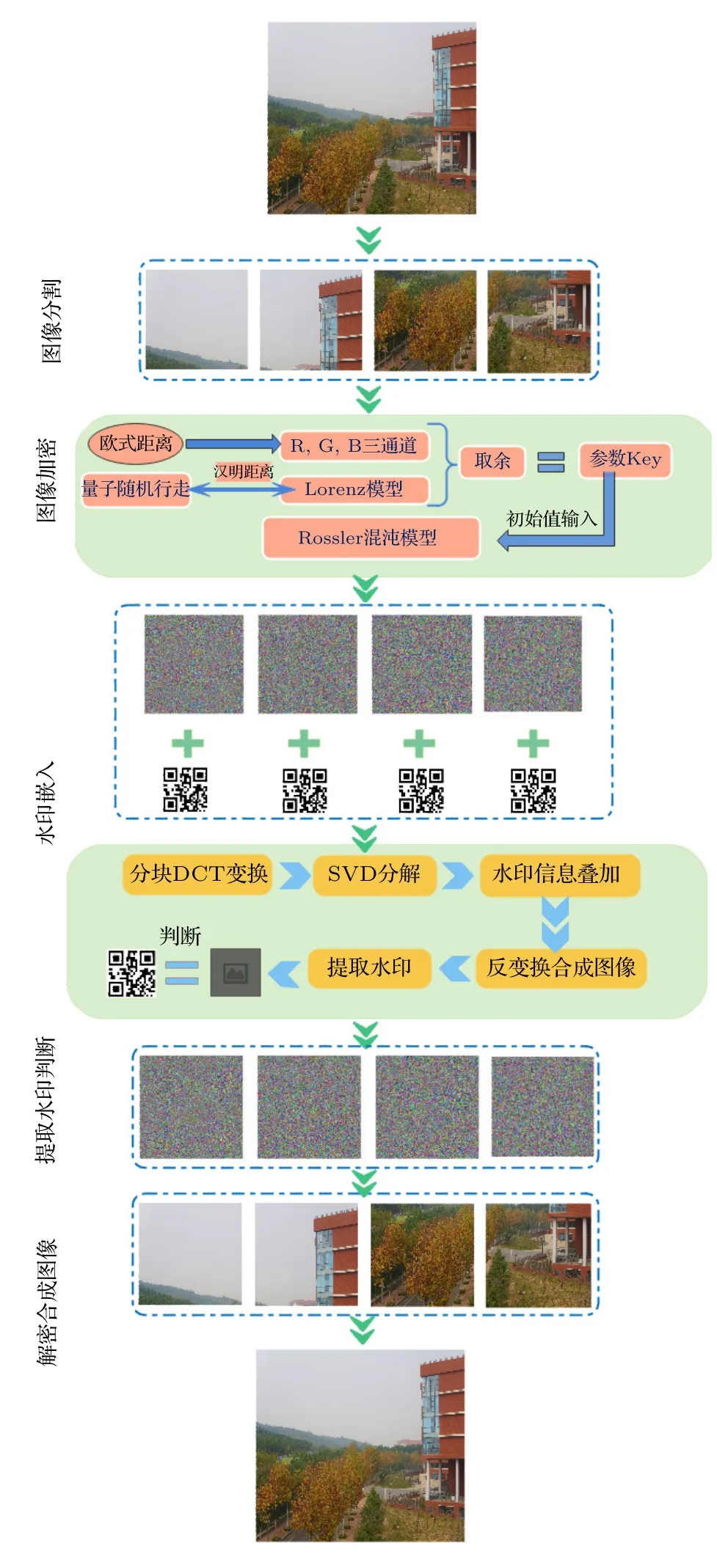
图8 加密-水印算法流程图Fig.8.Encryption watermark algorithm flow chart.

图9 加密仿真结果Fig.9.Encryption simulation results.

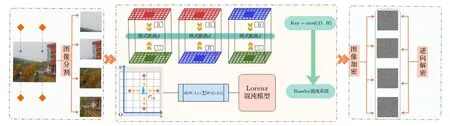
图10 加密算法Fig.10.Encryption algorithm.

4.2 加密性能分析

本节对加密图像进行了直方图、相关性、GVD、峰值信噪比等多方面的性能分析,加密后的图像峰值信噪比稳定在7—9 之间加密效果较好,GVD 评分接近1 说明加密后图像与加密前图像基本不同,加密图像的相关性均匀分布,其相关性系数接近0,且加密后的直方图分布均匀,实验结果表明本算法具有较高的抵御统计分析攻击的能力.

4.2.1 直方图

图像中各个灰度值的分布情况通过图像的直方图显示,恶意的第三方可针对密文图像的直方图表现出明显的统计规律来获取图像的信息.直方图的方差能有效量化加密算法抵御统计分析攻击能力.方差越小,说明像素分布越均匀,图像显示的统计信息就越少,图像加密方案就越安全.

3D 直方图以及原始图和加密图像的直方图如图11—图18 所示,可以看出原始图像及其RGB三通道的直方图分布极其不均匀,而经过加密后的图像及其RGB 三通道的直方图像素分布均匀,方差小无较大波动,图像显示的统计信息就越少,这表明加密图像抵抗统计攻击的效果较好,图像加密方案就越安全.

图11 原始图像1 和加密图像1 的3D 直方图Fig.11.3D histogram of original image 1 and encrypted image 1.

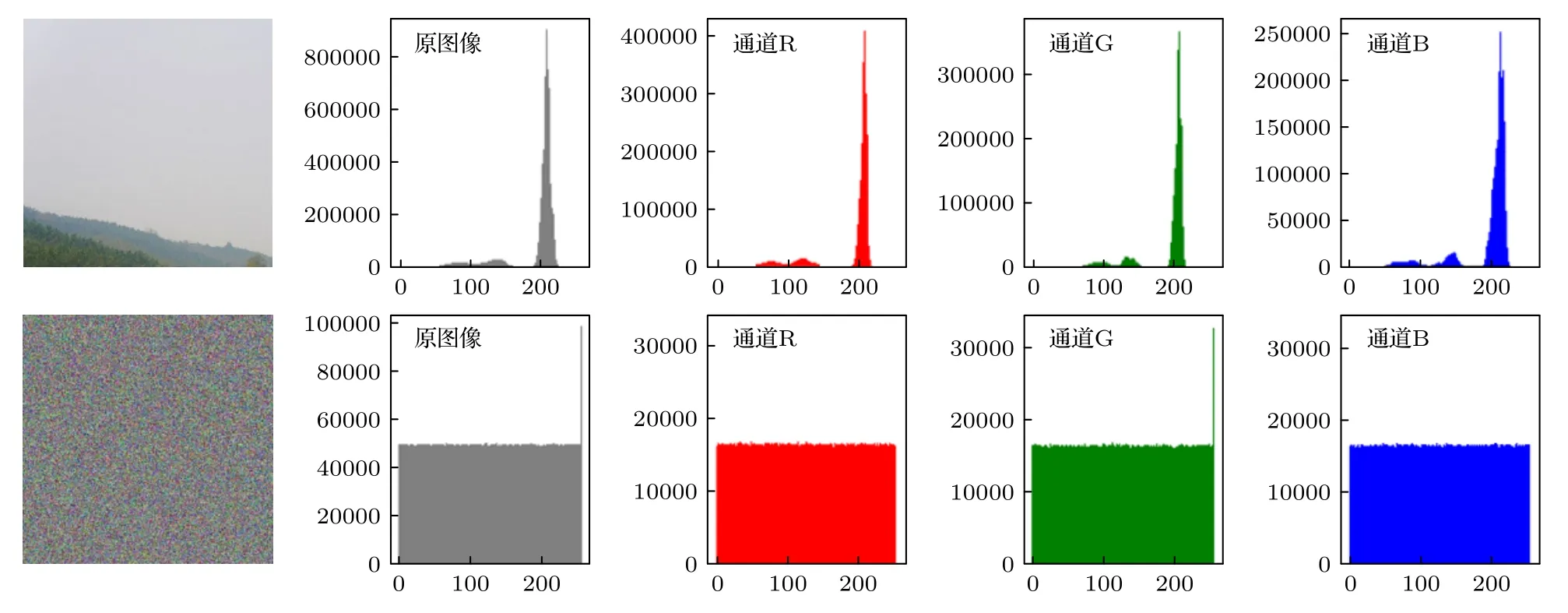
图12 原始图像1 和加密图像1 的性能分析直方图Fig.12.Performance analysis histogram of original image 1 and encrypted image 1.

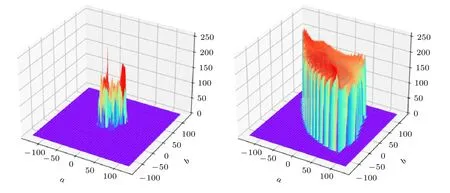
图13 原始图像2 和加密图像2 的3D 直方图Fig.13.3D histogram of original image 2 and encrypted image 2.

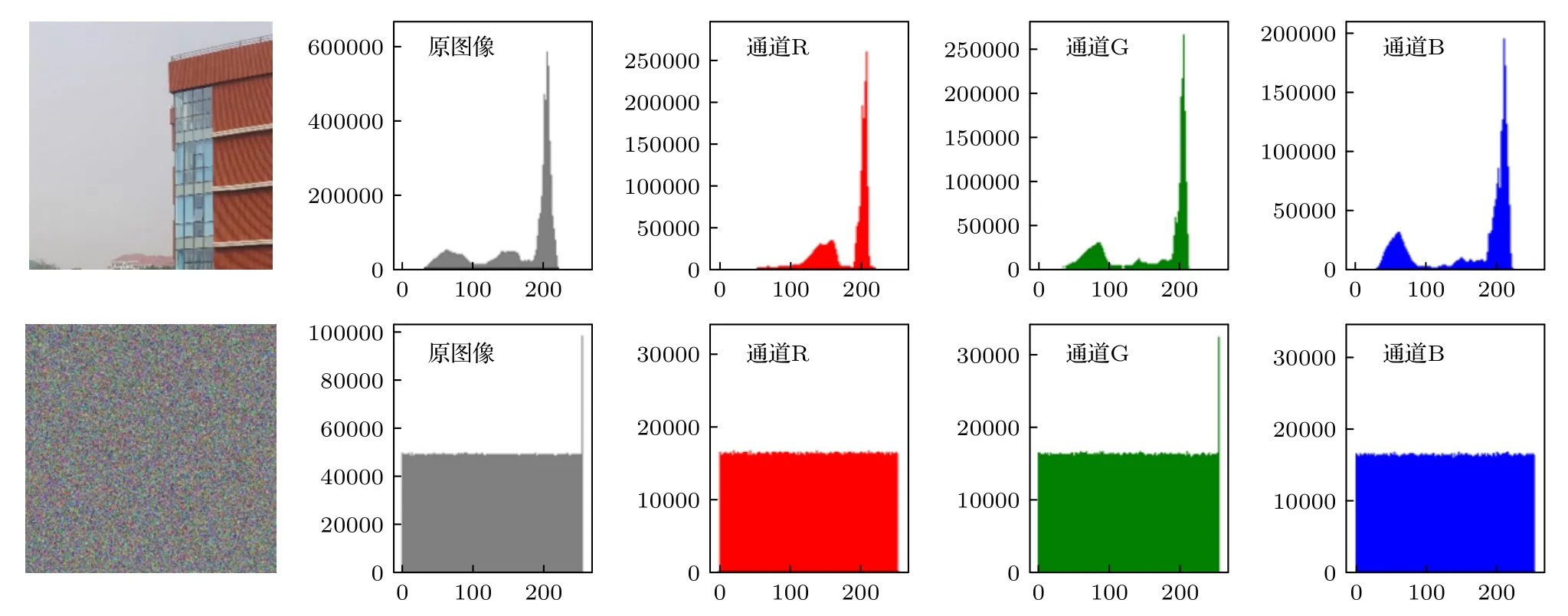
图14 原始图像2 和加密图像2 的性能分析直方图Fig.14.Performance analysis histogram of original image 2 and encrypted image 2.

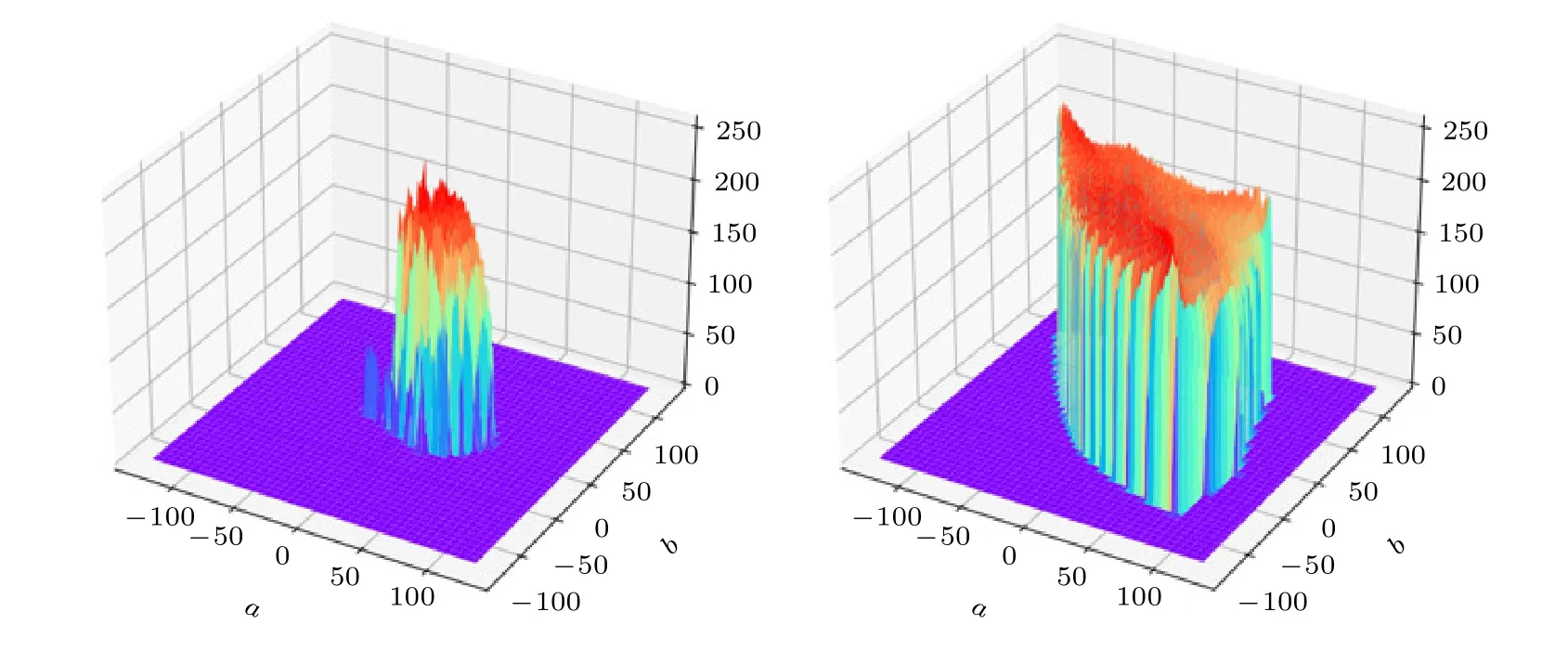
图15 原始图像3 和加密图像3 的3D 直方图Fig.15.3D histogram of original image 3 and encrypted image 3.

图16 原始图像3 和加密图像3 的性能分析直方图Fig.16.Performance analysis histogram of original image 3 and encrypted image 3.

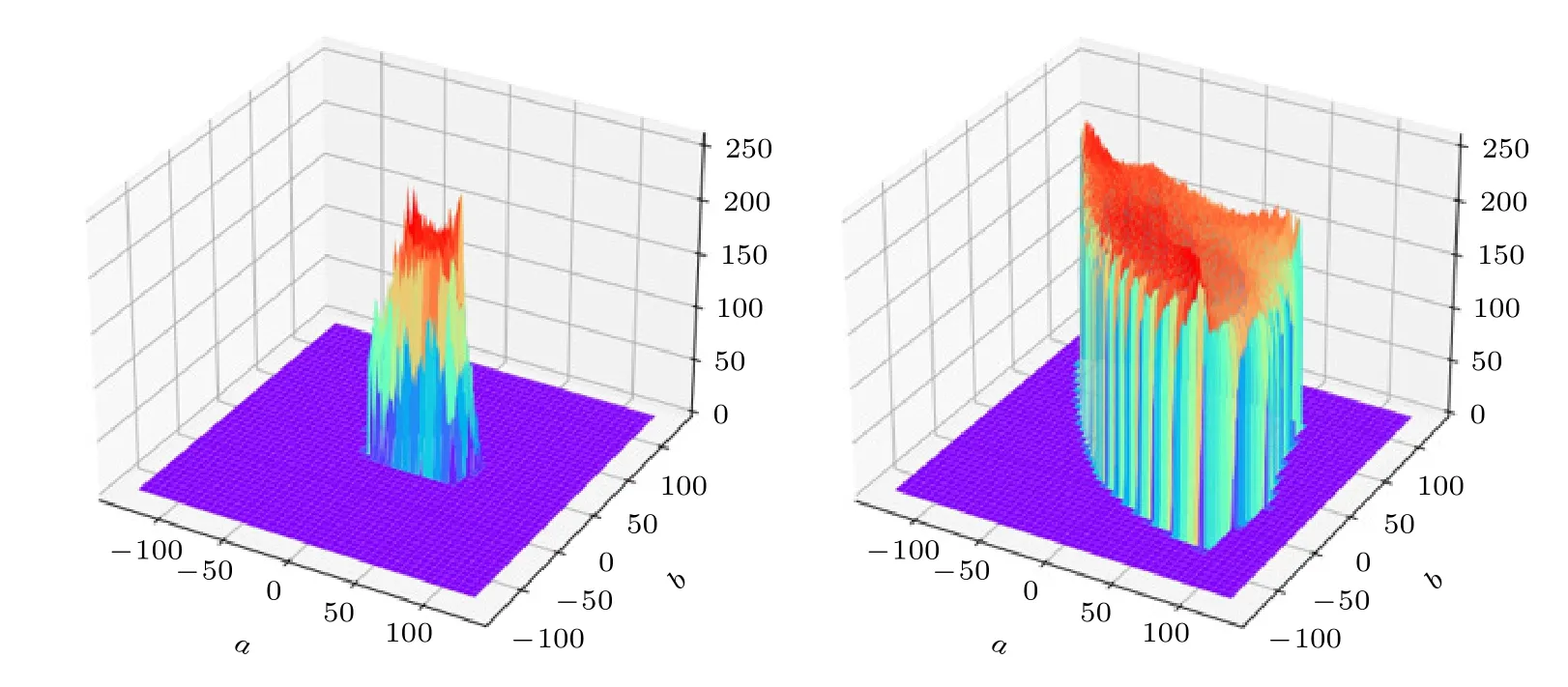
图17 原始图像4 和加密图像4 的3D 直方图Fig.17.3D histogram of original image 4 and encrypted image 4.

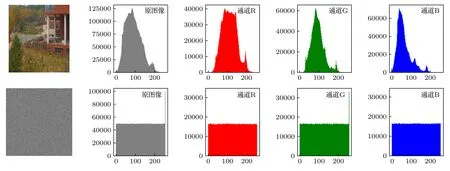
图18 原始图像4 和加密图像4 的性能分析直方图Fig.18.Performance analysis histogram of original image 4 and encrypted image 4.

4.2.2 像素相关性

图像的相关性分析是指对图像相邻像素之间进行分析,从而衡量像素之间的相关密切程度.一个像素往往会泄漏其周边像素的信息,攻击者往往根据某个像素点来预测出下一个像素值,实现对整个明文图像的恢复.数字图像中的相邻像素具有很强的相关性,这些强相关性必须被打破,以避免统计攻击.相关系数的计算公式如下:

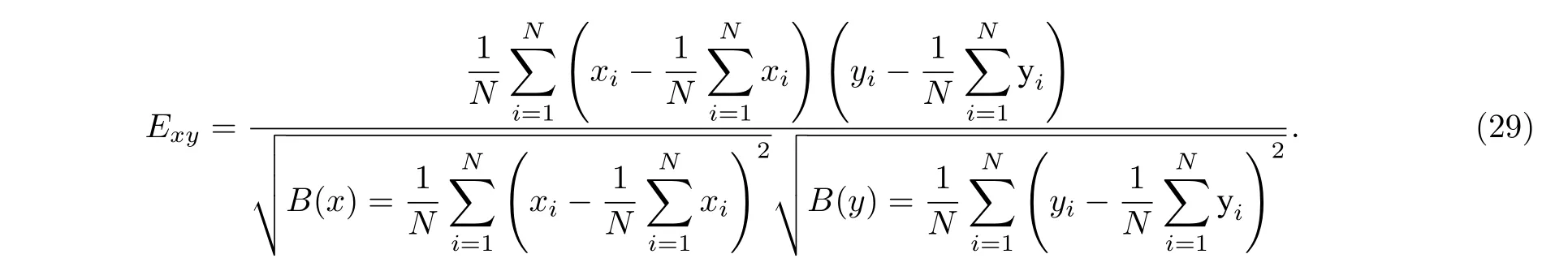
由图19—图22 可以清晰地看出原始图像的像素分布集中不均匀,但经过加密后的图像像素分布均匀.根据表1—表4 得到加密后图像的Horizontal,Vertical,Diagonald 的值接近0,这充分表明,我们的加密算法对图像加密以后打破原图像的强相关性,能有效地抵抗像素相关性分析的能力.

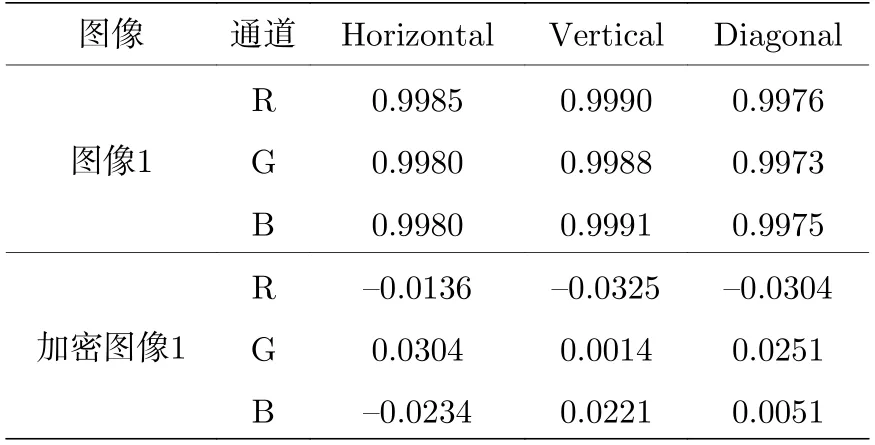
表1 原始图像1 和加密图像1 的相关性数值分析Table 1. Numerical analysis of correlation between original image 1 and encrypted image 1.

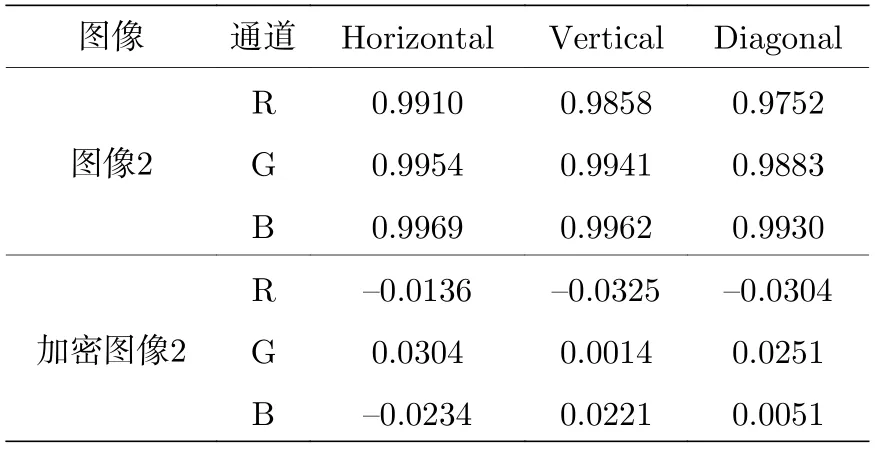
表2 原始图像2 和加密图像2 的相关性数值分析Table 2. Numerical analysis of correlation between original image 2 and encrypted image 2.

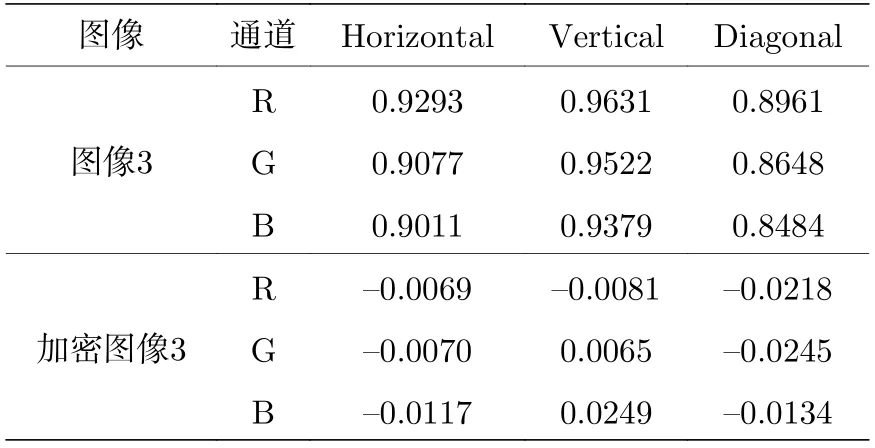
表3 原始图像3 和加密图像3 的相关性数值分析Table 3. Numerical analysis of correlation between original image 3 and encrypted image 3.

表4 原始图像4 和加密图像4 的相关性数值分析Table 4. Numerical analysis of correlation between original image 4 and encrypted image 4.

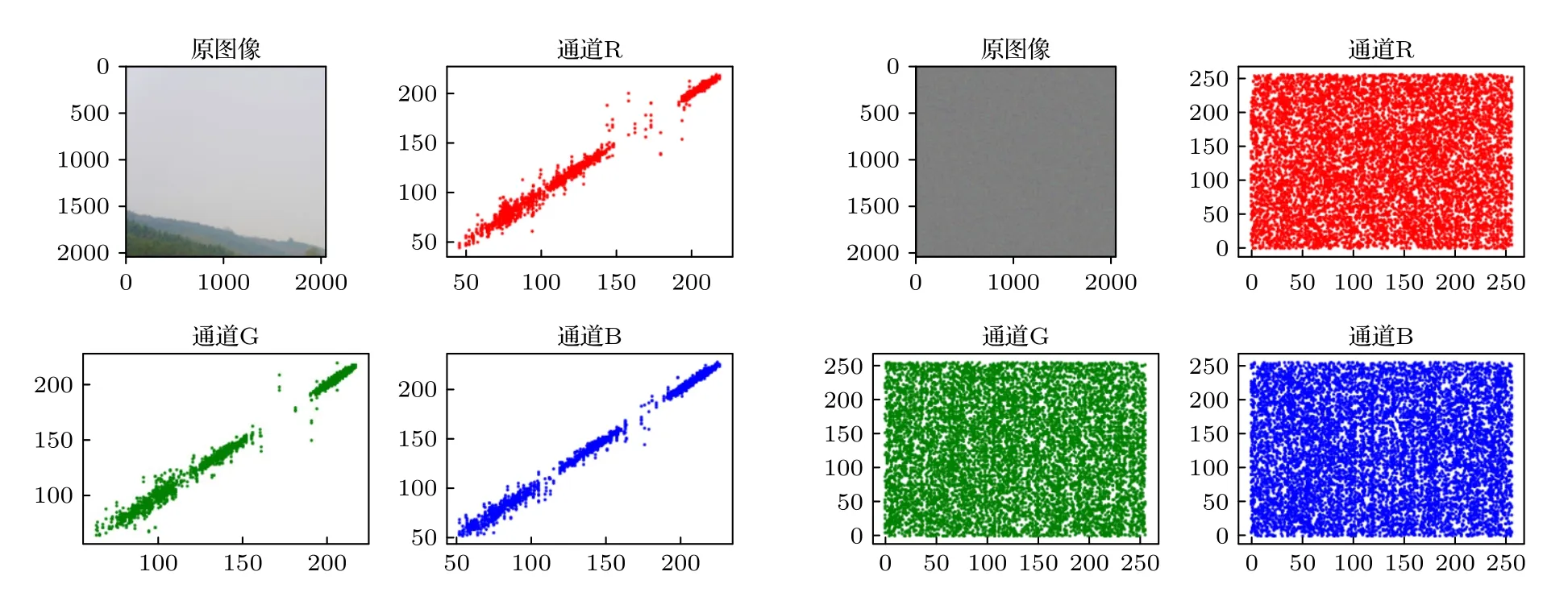
图19 原始图像1 和加密图像1 的相关性Fig.19.Correlation between original image 1 and encrypted image 1.

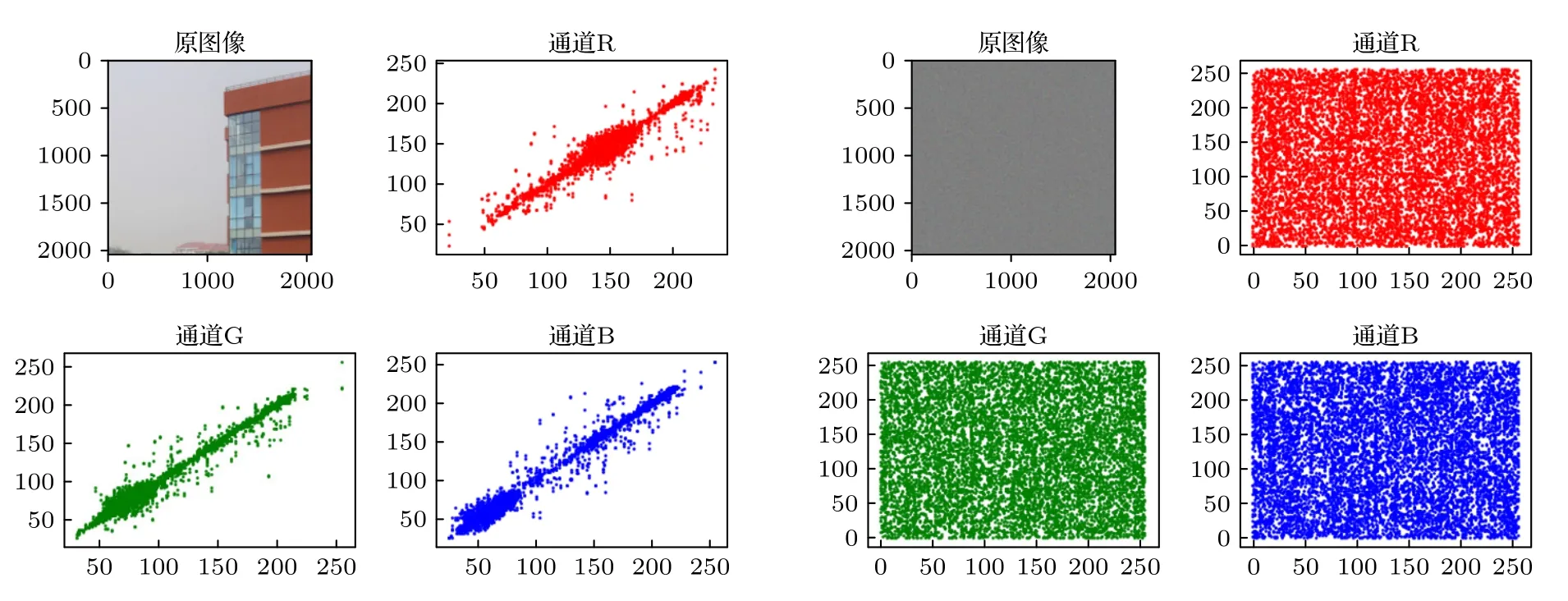
图20 原始图像2 和加密图像2 的相关性Fig.20.Correlation between original image 2 and encrypted image 2.

图21 原始图像3 和加密图像3 的相关性Fig.21.Correlation between original image 3 and encrypted image 3.

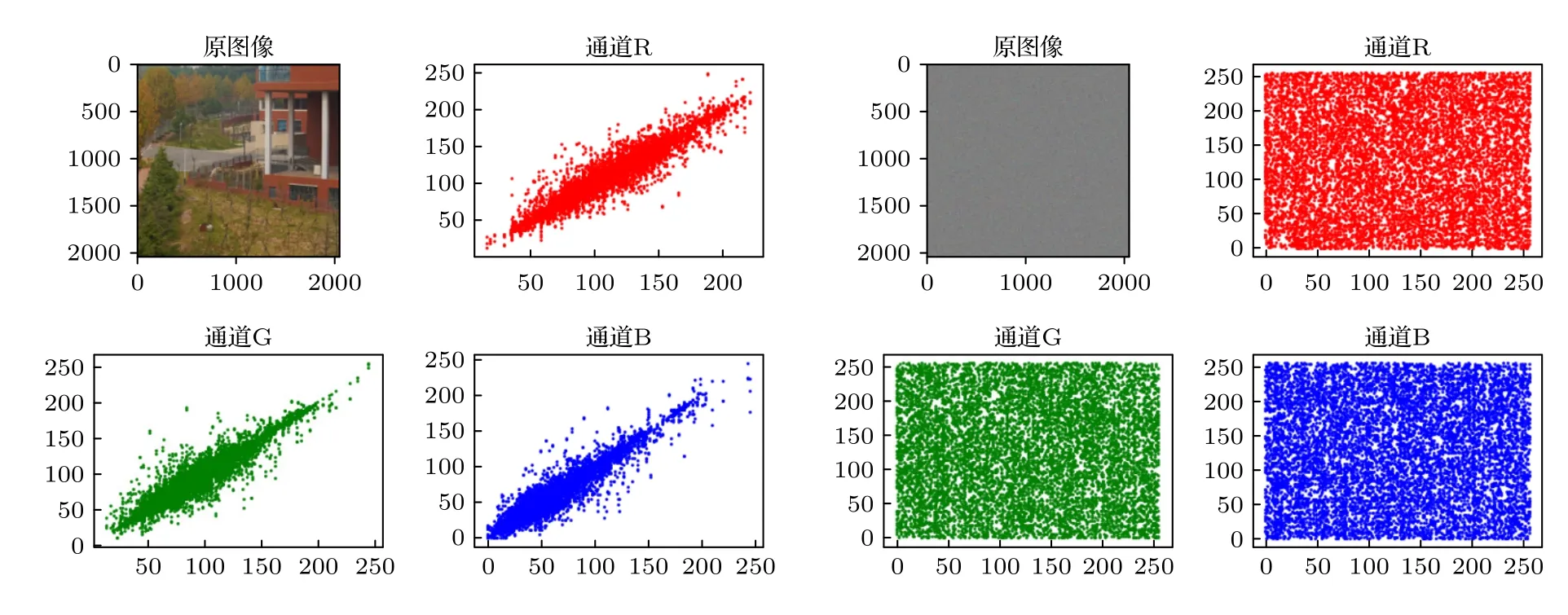
图22 原始图像4 和加密图像4 的相关性Fig.22.Correlation between original image 4 and encrypted image 4.

4.2.3 灰度差分析

灰度差分析(GVD)是比较原始图像和加密图像的随机性的另一种统计度量,可由下式定义:

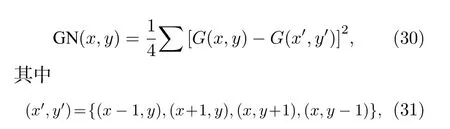
其中G(x,y) 表示位置 (x,y) 处的灰度值.整幅图像的平均邻域灰度差用下式计算:

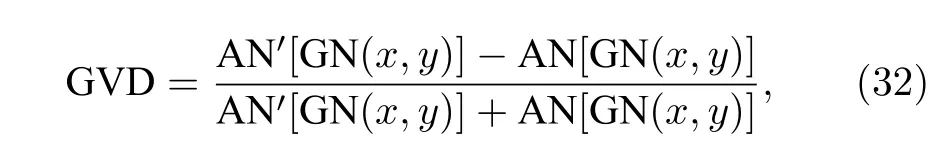
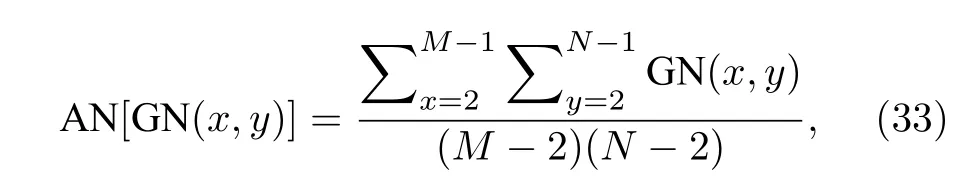
式中,A N 和 A N′代表平均邻域灰度值,但前者表示加密前,后者表示加密后.上述方程的最终结果称为GVD 评分,如果两幅图像完全相同,则GVD评分为0,否则为1,实验结果如表5 所示.

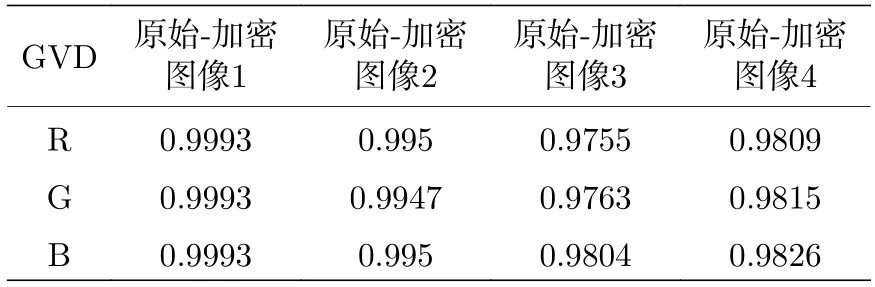
表5 GVDTable 5. GVD.

4.2.4 密钥敏感度分析

检测加密方案安全性的方法之一是密钥敏感度分析,本文通过实验对密钥生成序列中的某个比特值进行改变得到了完全不同的加密效果,并对前后两张加密图像的像素数变化率(NPCR)和统一平均变化强度 (UACI) 进行分析,实验结果如表6 所示,

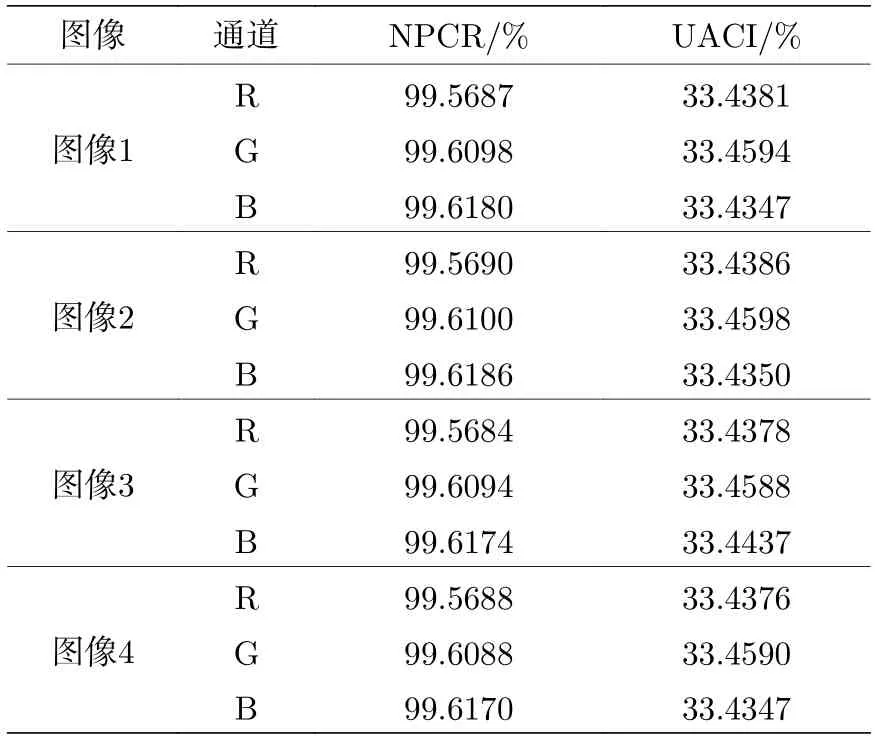
表6 密钥敏感性分析Table 6. Key sensitivity analysis.

表明其接近理想值NPCR=99.6094%,UACI=33.4635%,计算公式如下:

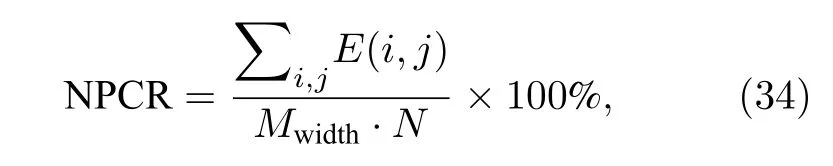
式中,Mwidth和N分别为两幅随机图像的宽度和高度,定义E(i,j) 为

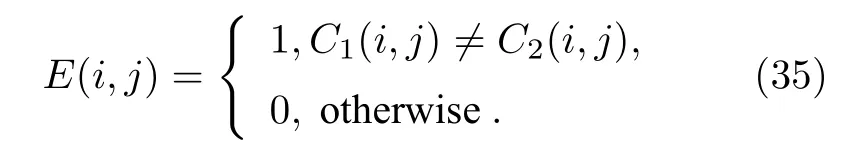
相应地,UACI 可以用来测量颜色分量对比度强度的平均值,计算公式如下:

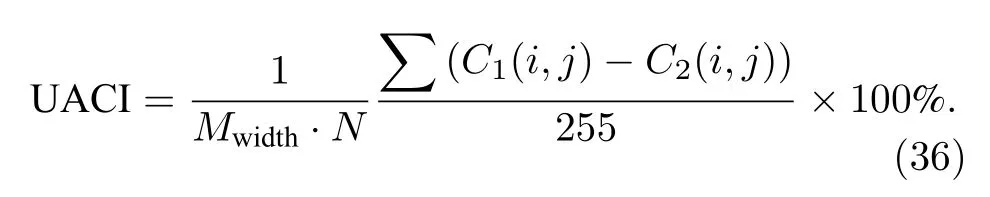
4.2.5 峰值信噪比

峰值信噪比(peak signal to noise ratio,PSNR)主要考察对应像素点之间的误差.给定大小为M×N的加密图像X和原图像Y,PSNR 计算如下:

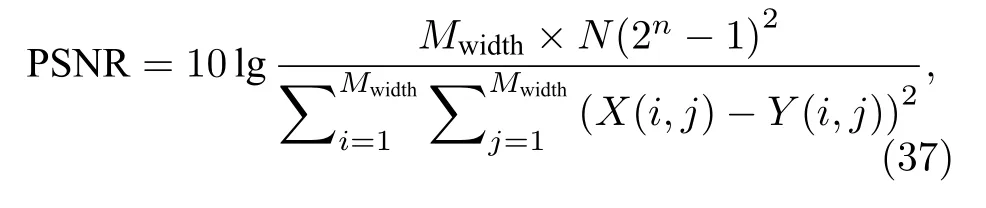
其中,Mwidth和N分别表示图像的宽高,n为像素位数;PSNR 值越大,表示失真越小,两张图片差距越小,加密效果越差.

由表7 峰值信噪比看出原始图像与加密图像1,原始图像加密图像2,原始图像加密图像3,原始图像加密图像4 的R,G,B 三通道的PSNR 值都稳定在7—9 之间.可以判断出原始图像与各个加密图像的差距较大,加密的效果较好.

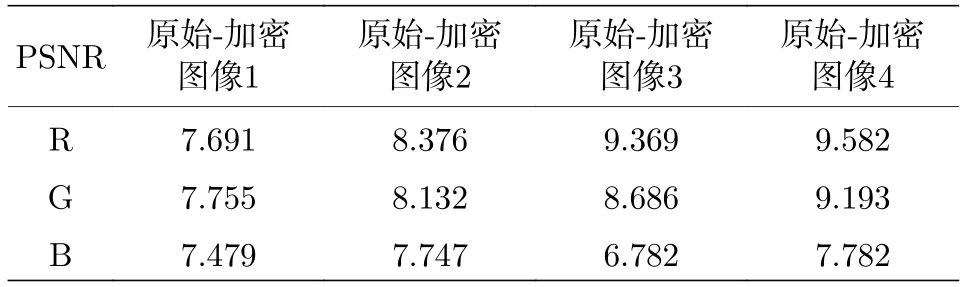
表7 峰值信噪比Table 7. Peak signal to noise ratio.

4.3 水印攻击检测

通过对水印嵌入的图像模拟各种攻击来检测水印的鲁棒性,对图像的攻击同时影响载体图片信息和提取的水印的信息.

4.3.1 嵌入水印的峰值信噪比

峰值信噪比主要考察对应像素点之间的误差.分别计算4 幅加密图像和嵌入水印图像的峰值信噪比,结果如表8 所列.

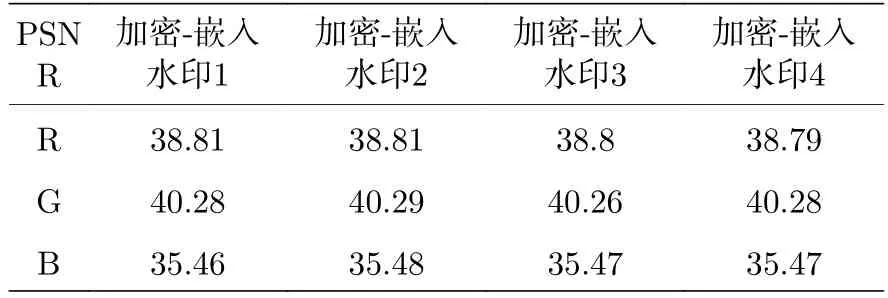
表8 嵌入水印的峰值信噪比Table 8. Peak signal to noise ratio of embedded watermark.

4.3.2 高斯噪声

高斯噪声是指概率密度函数服从高斯分布(即正态分布)的一类噪声,高斯噪声可以表示为

其中,C(x,y) 是 被添加高斯噪声后的图像,f(x,y)是原图像,c(x,y) 是高斯加性噪声,如图23 所示.

图23 高斯噪声Fig.23.Gaussian noise.

5 总结

本文提出一种新颖的基于量子随机行走和多维混沌的三维图像加密算法,利用量子计算的优势,改善了混沌系统的密钥的空间和随机性,使得密钥的敏感度较高,难以通过暴力求解的方式推出密钥.对该方案进行直方图、信息熵、相关性等性能分析,实验结果表明该算法安全可靠,能够抵抗统计攻击,在RGB 三通道之间进行像素置乱使得很难从一个通道求解另一个通道的解密图像.并且图像嵌入盲水印信息后,在传输中对恶意篡改图像起到了监听作用,一旦对图像攻击,在提取水印后,接收方就会知道传输过程中遭受攻击,进一步提高了图像传输过程中的安全性.