基于参数自整定PID的水下滑翔机航向控制方法

陈弈煿，张润锋，杨绍琼,2,3，张连洪,2,3，魏 鹏

(1.天津大学 机械工程学院 机构理论与装备设计教育部重点实验室，天津 300350；2.天津大学 青岛海洋技术研究院，山东 青岛 266237；3.青岛海洋科学与技术试点国家实验室 海洋观测与探测联合实验室，山东 青岛 266237)

水下滑翔机作为一种新型的水下移动观测平台，其具有功耗低、航程长、续航时间长及隐蔽性高的特点，可进行长时序、大范围的海洋观探测，是建设“透明海洋”工程的有效工具之一[1-4]。在无人值守的情况下提高水下滑翔机长时序观探测任务的能力是研究人员现阶段面临的主要挑战之一[5]。水下滑翔机动力学模型的非线性特点与海洋环境的复杂多变，导致其较难按照预设航向进行运动。因此，设计一种鲁棒的航向控制策略对于水下滑翔机的轨迹精准控制具有重要意义。

在水下滑翔机航向控制研究方面，PID(proportional-integral-derivative)控制器是现阶段水下滑翔机航向控制中应用最广泛的方法[6]。PID是基于线性控制的控制器，而水下滑翔机的运动具有非线性、时变等特点，PID控制有时无法满足快速准确的要求。Elmokadem等[7]采用滑模控制(sliding-mode control, SMC)进行了水下轨迹跟踪控制研究，并进行了仿真实验。滑模控制具有较好的鲁棒性，具有快速响应、对参数和扰动不敏感等特点，适合水下滑翔机控制，然而抖振现象为其显著缺点。Tchilian等[8]将水下滑翔机的非线性模型线性化后，实现了基于线性二次型调节器(linear quadratic regulator, LQR)的控制，并将该控制策略应用于水下滑翔机路径跟踪控制上，但该方法在非定常运动控制上难以实现；Lyu等[9]提出了一种基于神经网络的水下滑翔机的平衡参数的计算方法，并将其应用于水下滑翔机航向控制上，研究结果表明其具有良好的非线性处理和强大的自学习能力，但反向误差传播神经网络收敛时间过长，实际应用效果不理想。

为了解决控制器参数设定过程中可能存在反复调整以及参数非最优的情况，笔者利用径向基函数(radial basis function, RBF)神经网络可以快速逼近任意非线性函数的性质[10]，首先设计了神经网络的识别函数，然后利用梯度下降法对PID控制器参数进行自整定，使控制器参数能够快速调整，同时保证了控制器的性能，确保了水下滑翔机可在较短时间内调整到预定航向。

1 水下滑翔机动力学建模

水下滑翔机由自身的浮力变化提供驱动力，通过内部的姿态调节单元来改变自身姿态，并通过机翼实现滑翔运动[11]。天津大学“海燕-Ⅱ”水下滑翔机由壳体单元、浮力调节单元、姿态调节单元、通讯单元和传感器单元等组成。为了方便分析，将整个水下滑翔机系统简化为航行器主体、俯仰调节重块、横滚调节重块和浮力调节重块构成的模型。根据动量和动量矩定理，可推导出其六自由度动力学模型[12]，利用动力学模型分析其在水平面内的运动。

建立图1所示的水下滑翔机的大地坐标系E-xyz，体坐标系B-xyz。在体坐标系下，定义水下滑翔机速度v=(u,v,w)T，角速度坐标w=(p,q,r)T；在大地坐标系下，定义水下滑翔机位置为O=(x,y,z)T，姿态坐标为Ω=(φ,θ,ψ)T。由于只研究水下滑翔机的航向控制相关问题，下面仅列出水下滑翔机水平面内横向运动的数学模型。运动模型各参数赋值如表1所示。

续表1

图1 水下滑翔机坐标系示意图Fig. 1 Underwater glider coordinate system

水下滑翔机水平面内动力学方程为

(1)

运动学方程为

(2)

2 RBF-PID控制器

2.1 RBF神经网络原理

RBF神经网络于1988年提出[13]。相比其他类型神经网络，RBF网络由于具有良好的泛化能力，网络结构简单和能够避免不必要的计算而备受关注。由于RBF神经网络具有逼近任意非线性函数的能力，所以被广泛应用于非线性控制领域[14]。RBF神经网络是一个包含输入层、隐含层和输出层的前馈网络。采用多输入单输出的神经网络，其网格结构如图2所示。从系统的动力学模型可知，水下滑翔机具有非线性特性，因此，将RBF神经网络和PID控制器相结合，设计了水下滑翔机RBF-PID航向控制器。

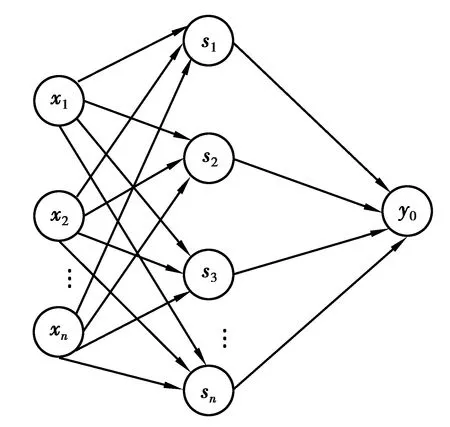
图2 径向基函数神经网络结构图Fig. 2 Radial basis function neural network structure diagram

RBF神经网络结构模型的第1层为输入层,x=[x1,x2,…,xn]T为输入向量。第2层为隐含层,是由径向基函数构成的神经元激活函数，具有m个节点隐含层向量为s=[s1,s2,…,sm]T，其中

(3)

式中:cj为第j个节点的中心矢量，cj=[cj1,cj2,…,cji,…,cjn]T，(i=1,2,…,n)；bj为隐含层第j个神经元高斯基函数的宽度。

RBF网络权值为

w=[w1,w2,…,wm]T。

(4)

RBF网络输出为

y(k)=wTh=w1h1+w2h2+…+wmhm。

(5)

网络逼近性能指标为

(6)

利用梯度下降法迭代输出权值、节点中心值和节点基宽参数：

wj(k)=η[y(k)-y0(k)]sj+α[wj(k-1)-wj(k-2)]+wj(k-1)，

(7)

(8)

(9)

式中：η为学习效率；α为动量因子。

2.2 控制器设计

水下滑翔机航向控制的目的是使其跟踪期望轨迹，即航向跟踪误差在有限时间内收敛。采用的控制系统结构如图3所示。

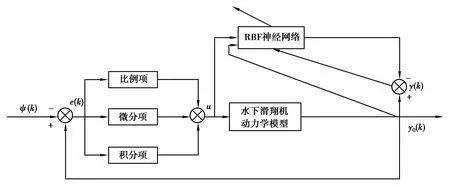
图3 控制系统结构图Fig. 3 Structure diagram of control system

令航向角误差为

e(k)=ψ(k)-y0(k)，

(10)

式中：ψ(k)为期望航向角；y0(k)为实际航向角。

为保证水下滑翔机按预期路径运动，要尽量保证航向角误差为0。选取神经网络整定目标为

(11)

PID控制器的输出u(k)为

u(k)=u(k-1)+kP(k)(e(k)-e(k-1))+kI(k)e(k)+kD(k)(e(k)-2e(k-1)+e(k-2))，

(12)

式中kP，kI，kD的值采用梯度下降法求取，即

(13)

(14)

(15)

(16)

对于给定的期望航向角ψ(k)，被控对象(即水下滑翔机动力学模型)的输出为y0(k),RBF神经网络的输出为y(k)，根据两者的差值利用公式(7)(8)(9)更新wj(k),bj(k),cji(k),将它们带入公式(16)可得到被控对象Jacobian信息阵，再将所得结果代入公式(13)(14)和(15)中更新kP,kI,kD，从而使PID控制器产生新的控制量u，该控制量对应的水下滑翔机内部电池包的滚转角度使其产生新的实际航向角。

3 数值仿真

为验证所提出的基于RBF神经网络参数自整定的控制算法的有效性，在MATLAB中进行仿真，并引入PID算法进行对比。仿真开始设置期望航向角为30°。对比试验中PID控制器参数由仿真试验得到，参数设置为：kP=0.7，kI=1.3，kD=0.7；RBF-PID参数初值kP0=0.1，kI0=0.1，kD0=0.1。海浪干扰D(t)=sin(0.01t)。学习效率η= 0.5，动量因子α= 0.05。输入权值、节点中心值和节点基宽初值均设置为0。

图4为方波信号时航向RBF-PID控制器参数自整定曲线，可以看出，在航向变化时，RBF-PID控制器能快速完成对参数的调整，达到期望的控制效果。对于方波信号航向控制曲线(图5)，当航向剧烈变化时，PID控制会出现较大的超调量，而RBF-PID控制航向变化较为平缓，且收敛速度较快；图6为两种控制方法的误差曲线，可以看出，采用RBF-PID算法仿真的航向角误差相对较小，且收敛时间较短。表2为仿真实验中两种控制方法的指标对比。可以看出，所提算法在方波信号输入下，均方误差下降了1.67%。

图4 方波信号时控制器参数自整定曲线Fig. 4 Self-tuning curves of controller parameters at square signal

图5 方波信号航向控制曲线Fig. 5 Heading control curves of square signal

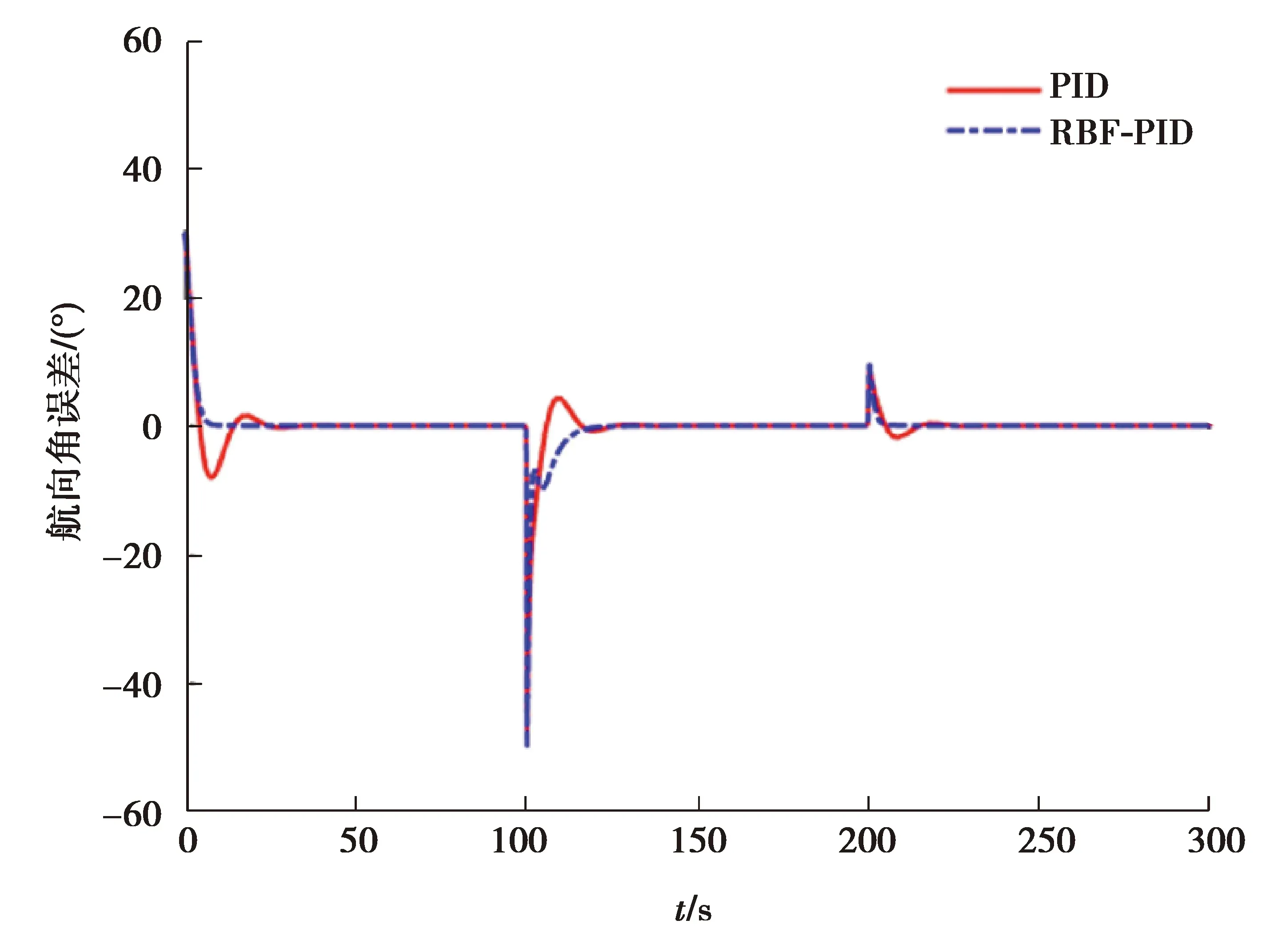
图6 方波信号航向控制误差曲线Fig. 6 Heading control error curves of square signal

表2 方波信号航向控制中PID与RBF-PID指标对比

为验证所提RBF-PID算法对时变航向的跟踪性能，在仿真中控制器的输入采用正弦信号。图7为正弦信号输入时RBF-PID航向控制器参数自整定曲线，可以看出，控制器的参数同样可以实现快速整定。图8为正弦信号输入时RBF-PID航向控制器控制曲线，控制器误差曲线如图9所示。从图中可以看出，随着时间的增加，两种方法皆可实现航向跟踪，但开始时PID控制出现较大超调量，收敛时间约为13 s，而RBF-PID控制超调量较小且收敛时间约为8 s，同时航向跟踪效果好，曲线较为平滑。表3为仿真实验中两种控制方法的指标对比。可以看出，所提算法在正弦信号输入下，最大超调量下降了5.28°，稳态误差下降了10%，收敛时间缩短了38%。

图7 正弦信号时控制器参数自整定曲线Fig. 7 Self-tuning curves of controller parameters at sinusoidal signal

图8 正弦信号航向控制曲线Fig. 8 Heading control curves of sinusoidal signal

图9 方波信号航向控制误差曲线Fig. 9 Heading control error curves of sinusoidal signal

表3 方波信号航向控制中PID与RBF-PID指标对比

4 结 语

针对水下滑翔机传统PID控制方法无法实现快速精确调整航向的问题，提出了一种RBF-PID的航向控制方法。由仿真实验结果可知，所提方法与传统PID控制相比具有更好的动态性能，即能够更快地实现航向跟踪，而且可实现参数快速自整定，减少了工作量。具体地，与PID控制方法相比较，设计的RBF-PID航向控制在方波信号输入下，均方误差下降了1.67%；正弦信号输入下，稳态误差下降了10%，收敛时间缩短了38%。笔者主要工作是针对水下滑翔机二维平面内运动进行了航向控制器设计及仿真，研究结果表明RBF-PID控制器鲁棒性强，控制精度较高，在水下滑翔机航向控制中具有很好的应用前景。同时由于实际海洋环境的不确定性较多，仿真实验很难完全地模拟真实海洋环境，为了进一步验证所设计控制器的性能，未来会进行海上试验验证。