活塞发动机止动轮毂传动系统动态特性分析

胡 珑，黄 友，周 丹，宋朝省，魏长旭

(1.重庆大学 机械传动国家重点实验室，重庆 400044；2.重庆宗申航空发动机制造有限公司，重庆 400054)

止动轮毂传动系统作为活塞发动机动力系统的重要组成部分，是保证发动机正常工作的关键部件，其动态特性直接影响发动机可靠性和稳定性。然而，由于发动机止动轮毂系统存在啮合面几何形貌复杂、动态接触机理不清及载荷工况复杂等问题，其振动冲击问题一直是困扰活塞发动机整体动态系统提升的关键因素之一，所以开展止动轮毂传动系统动力学建模与动态特性分析研究对揭示活塞发动机止动轮毂传动系统振动机理，提升整机性能具有重要的理论意义与工程应用价值。

近年来国内外学者针对活塞发动机动力装置、起动特性和增压特性等进行了一定的研究。鲍梦瑶等[1]建立了发动机与涡轮增压器的系统仿真模型，提出了一种能实现对增压器失效关键影响因素分级的分析法。徐斌等[2]通过研究发动机的增压性能，提出了基于实验的活塞发动机二级增压压比分配方案的方法。王兆铭等[3]基于某型航空发动机研究平台，讨论了高原环境下的起动供油控制规律。Moorthy等[4]建立了能实时、准确地反映真实发动机运行工况的航空活塞发动机模型，并进行了模拟仿真。Singla等[5]为了改善某型号发动机的性能，对其进气歧管开展了研究。Crosbie等[6]开展了一定压力和温度范围下的发动机高空性能测试实验，提出了安装节气门燃料喷射系统能让发动机的高空性能得到提升的方法。

笔者在分析活塞发动机止动轮毂系统结构和工作原理的基础上，建立了止动轮毂传动系统三维实体模型和解析动力学模型；采用Adams多体动力学软件建立了止动轮毂传动系统动力学仿真模型，通过对比分析，相互验证了动力学模型正确性，在此基础上研究了不同轴向预紧力和扭矩工况对止动轮毂系统动态特性的影响规律。

1 发动机止动轮毂传动系统结构与工作原理

活塞发动机止动轮毂传动系统三维模型如图1所示，主要由输出轴、止推半环、小齿轮、螺旋桨齿轮与止动轮毂组成。其中，螺旋桨齿轮与输出轴连接部分轴上有套筒，螺旋桨齿轮与小齿轮间连有垫圈，止动轮毂与3个串联的碟簧相连，受到碟簧的轴向预紧力。止动轮毂传动系统结构如图2所示。

图1 止动轮毂传动系统三维模型Fig.1 Three-dimensional model of doghub transmission system

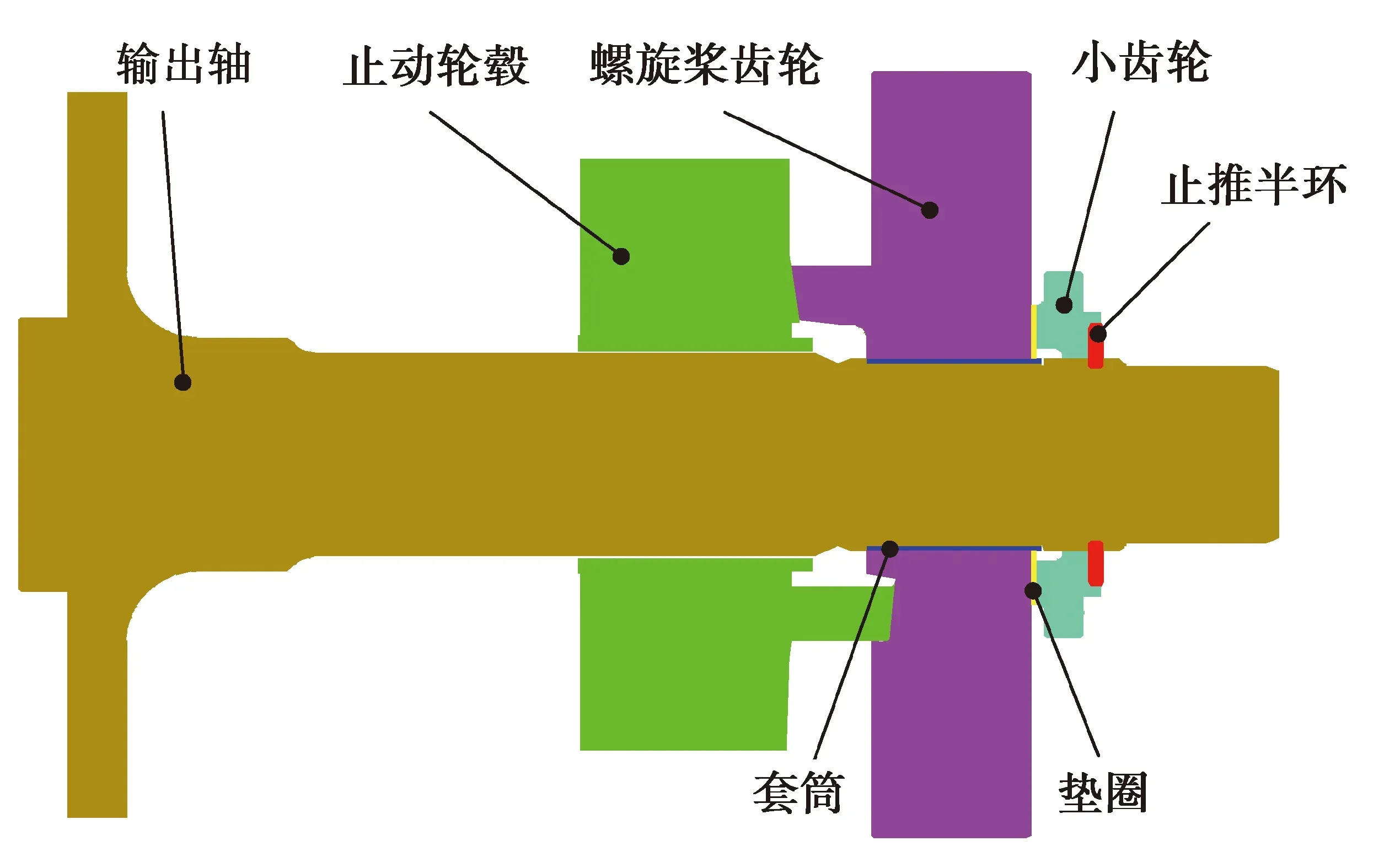
图2 止动轮毂传动系统结构图Fig. 2 Structure diagram of doghub transmission system

止动轮毂传动系统各零件材料具体参数如表1所示。

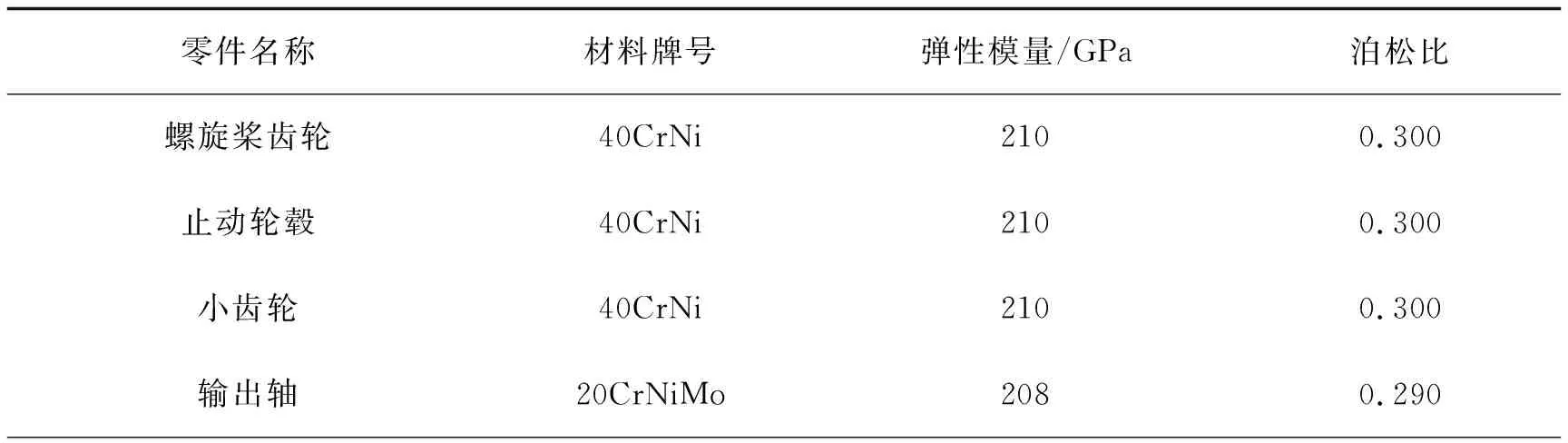
表1 材料参数

续表1

止动轮毂传动系统工作原理如图3所示，其动力来源于与曲轴固连的动力输入齿轮，通过与螺旋桨齿轮啮合传递到螺旋桨齿轮，螺旋桨齿轮再与止动轮毂通过曲面接触将动力传递到止动轮毂，最后由止动轮毂通过花键连接将动力传递到输出轴，完成止动轮毂传动系统的整个动力传递过程。

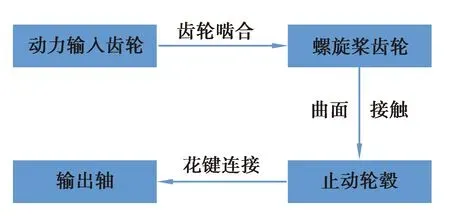
图3 系统动力传递路线Fig. 3 Transmission route of system power

止动轮毂与螺旋桨齿轮的动力传递通过其三爪曲面接触传递，如图4所示。当系统启动时，螺旋桨齿轮绕输出轴转动，其凸爪顶部与止动轮毂凸爪底部相接触，由于螺旋桨齿轮轴向位移自由度被止推半环限制，在接触力的作用下，止动轮毂凸爪沿着螺旋桨齿轮凸爪的曲面轴向移动，从螺旋桨齿轮凸爪底部的过渡圆弧段“爬坡”到凸爪工作斜面段，最后稳定在工作斜面与螺旋桨齿轮一同旋转。当稳定在工作斜面段后，止动轮毂接触副的受力情况如图5所示(图中下标p表示螺旋桨齿轮，g表示止动轮毂)。其中，AB段为过渡圆弧段，BC段为工作斜面段。

图4 止动轮毂螺旋桨齿轮接触副Fig. 4 Doghub-airscrew gear contact pair

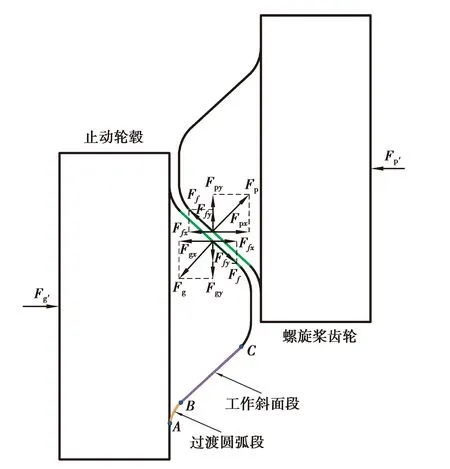
图5 止动轮毂接触副受力图Fig. 5 Force diagram of doghub contact surfaces

2 止动轮毂传动系统解析动力学模型

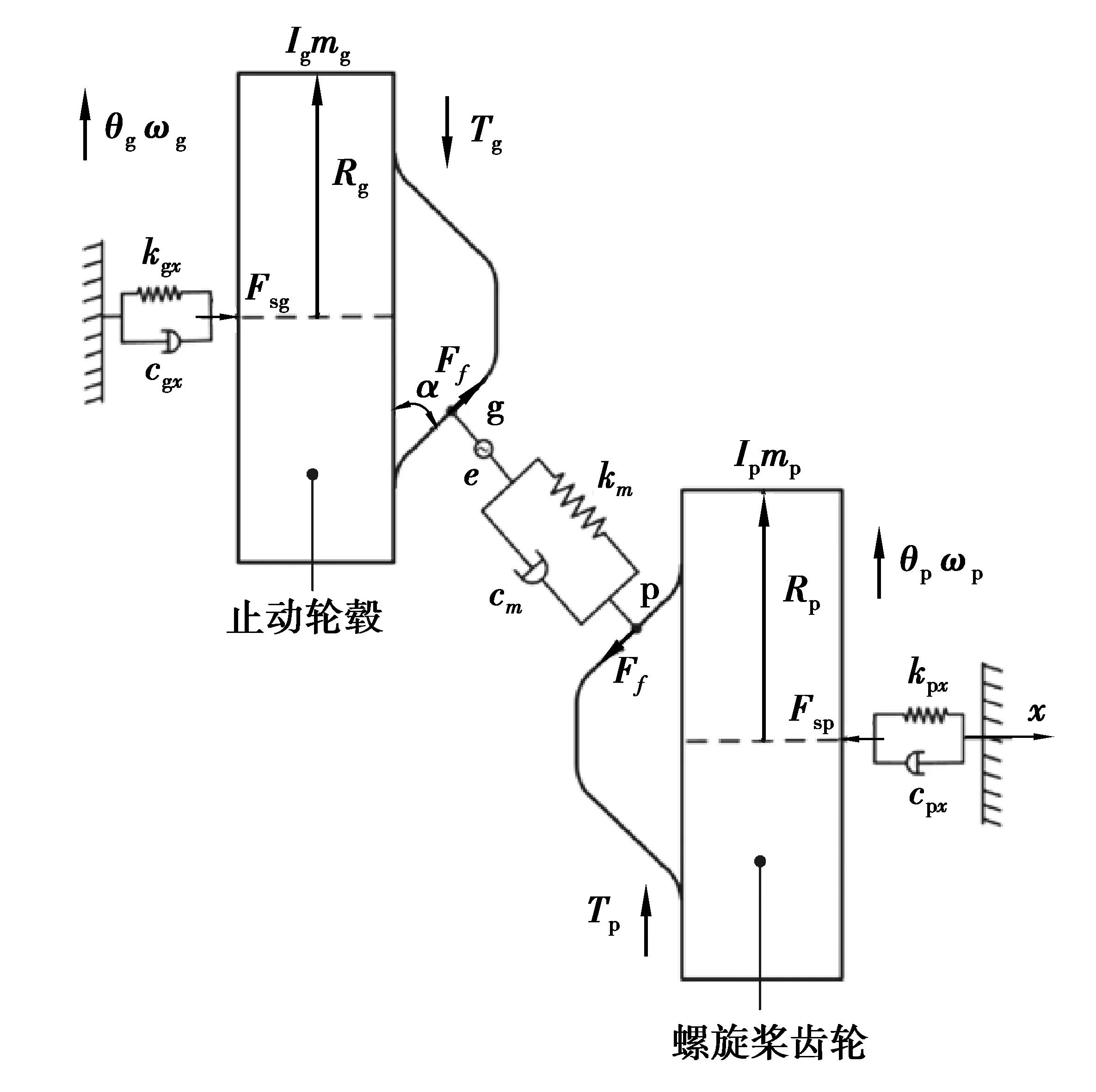
图6 止动轮毂系统动力学模型Fig. 6 Dynamic model of the doghub system

如图6所示，设螺旋桨齿轮p为主动轮，止动轮毂g为从动轮，三爪斜面的倾角为α，三爪的动力学模型建立在中间平面上，其等效接触半径可表示为

(1)

系统的广义位移列阵δ可表示为

δ={xpθpxgθg}T,

(2)

式中xi，θi(i=p,g)分别为主、从动轮在x向的平移振动位移和轴向振动位移。

系统的动能为

(3)

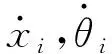
系统的势能、耗散能分别为

(4)

(5)

式中：δ为各方向投影到啮合线上的变形量，变形量压缩方向定义为正；Kix、Cix分别为主、从动轮的支撑刚度和阻尼；Km，cm分别为主从动轮啮合处的啮合刚度和啮合阻尼。

其中x，θ方向振动投影到啮合线方向的变形量分别为

δx=(-xp+xg)cosα，

(6)

δθ=(-Rpθp+Rgθg)sinα。

(7)

则系统各向振动投影到啮合线方向的总变形为

δ=δx+δθ=(-xp+xg)cosα+(-Rpθp+Rgθg)sinα，

(8)

(9)

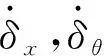
xp方向受到的外力为

(10)

θp方向的力矩为

(11)

xg方向受到的外力为

(12)

θg方向产生的力矩为

(13)

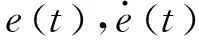
根据拉格朗日能量方程

(14)

则有

通过有限元求得模型的啮合刚度为

km=1.245×1013N/m。

3 止动轮毂系统动力学仿真模型

基于Adams多体动力学软件平台，进行止动轮毂系统动力学仿真模型的建立以及后续的仿真分析。动力学仿真模型的建立具体如下：

1)首先将系统中各个零件三维模型导入，分别进行位置坐标的变换，使零件的几何旋转轴线位于Z轴上，方便后续边界的建立。然后将各个零件按照对应关系进行装配。

2)设定模型的材料属性。将模型从三维软件导入后，会丢失零件材料的物理属性，所以需要按表1参数分别赋予各个零件的材料属性。

3)设置模型运动副约束。止动轮毂系统各个零件约束条件如表2所示。

表2 模型的约束关系

5)定义各个零件之间的接触时，选择基于碰撞函数的接触算法,接触类型选择Solid to Solid，摩擦类型选择Coulomb。其中接触参数主要包括材料接触刚度、力指数、接触阻尼、穿透深度以及动摩擦系数,具体接触参数取值如表3所示。

表3 接触参数

设置完成后的止动轮毂系统动力学仿真模型如图7所示。

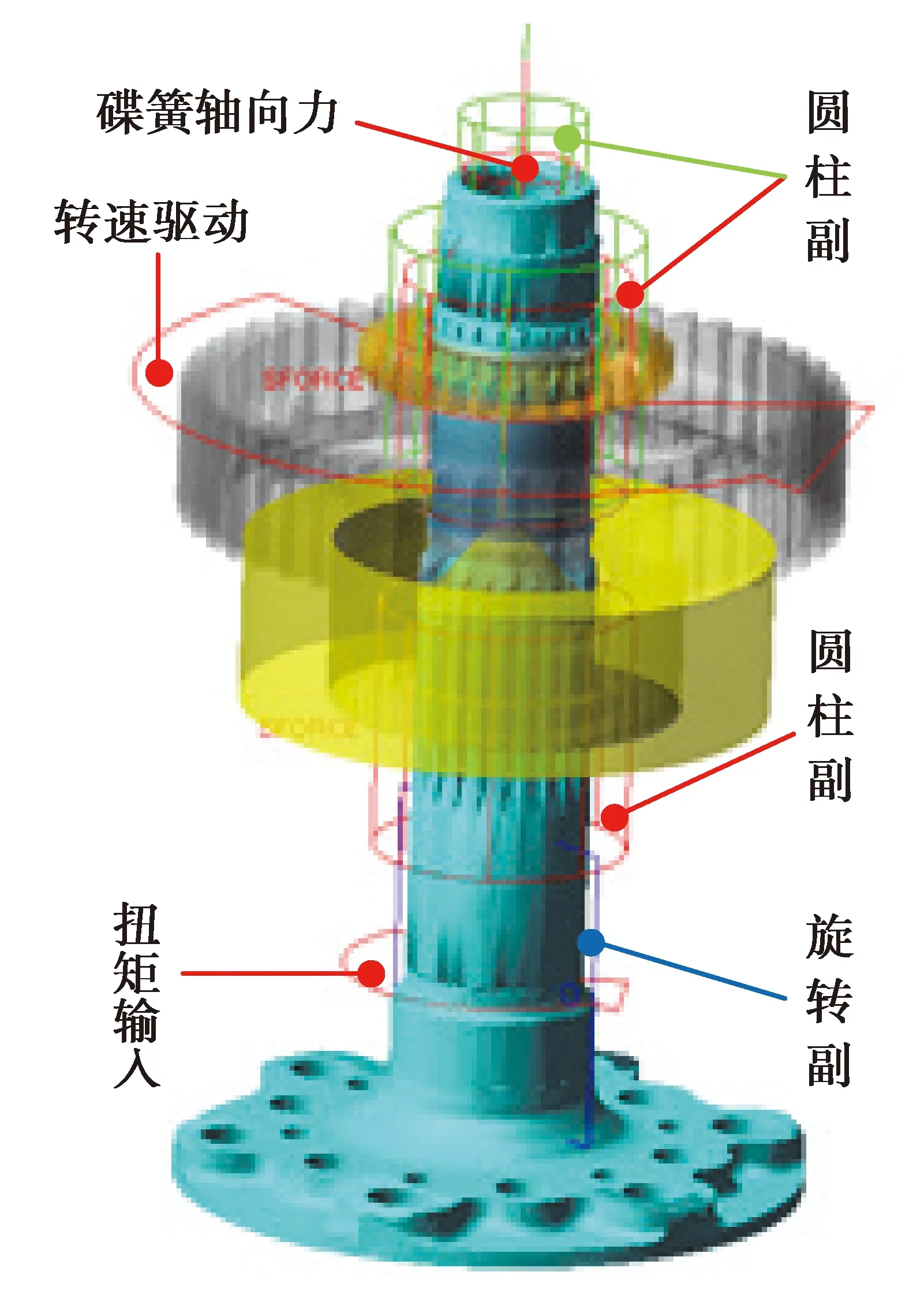
图7 系统动力学仿真模型Fig. 7 System dynamics simulation model

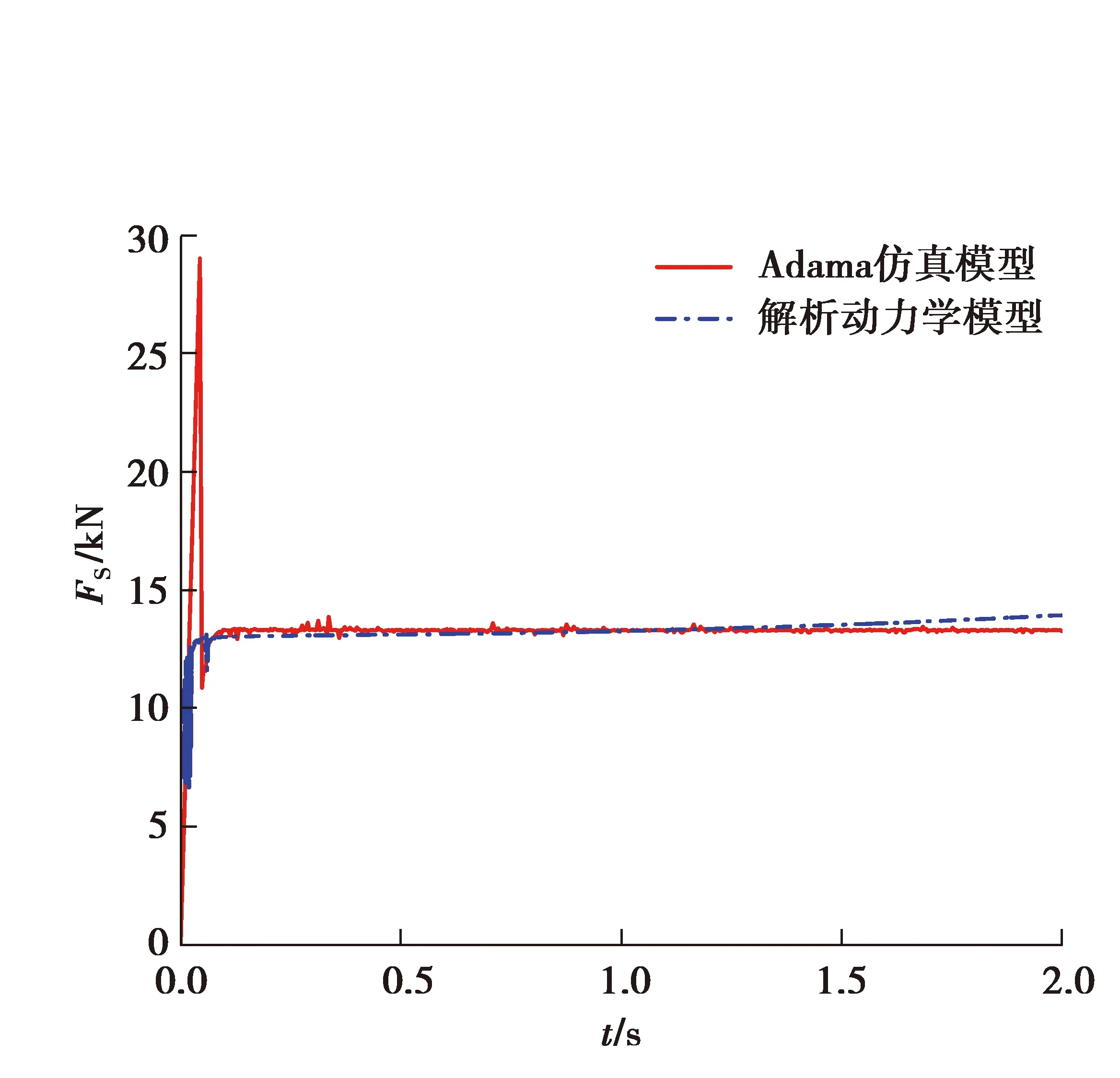
图8 两种模型轴向力结果对比Fig. 8 Comparison of axial force results of two models

由图8可知，在额定工况下，解析动力学计算出的轴向力更快地趋于平稳，最后稳定在13 942 N附近小幅波动，Adams计算的轴向力在初始阶段波动较大，然后逐步趋于平稳，最后稳定在13 300 N附近小幅波动。解析动力学的计算结果与Adams的计算结果对比，在稳定之后的误差约为4.6%，相互验证了动力学模型的正确性。

4 动态特性分析

为揭示活塞发动机止动轮毂传动系统振动机理，在额定转速下，进行不同扭矩和不同轴向预紧力对止动轮毂系统动态特性的影响分析。其中额定输入转速如图9所示。

图9 额定输入转速Fig. 9 Rated input speed

4.1 不同扭矩对系统动态特性的影响分析

图10 不同扭矩下的止动轮毂轴向力Fig. 10 Axial force of doghub under different torques

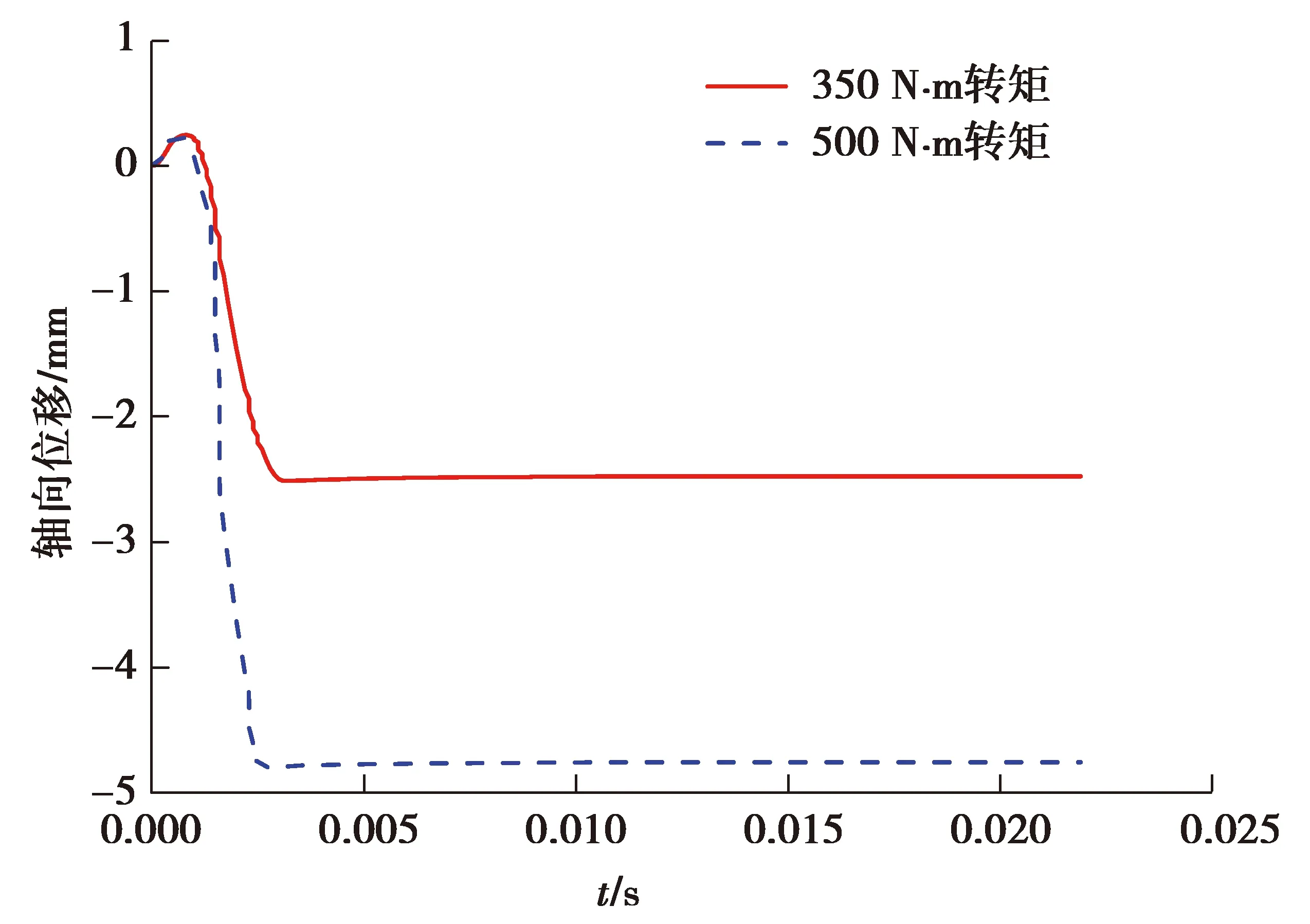
图11 不同扭矩下的止动轮毂轴向位移Fig. 11 Axial displacement of doghub under different torques

图12 350 Nm扭矩的止推半环轴向力Fig. 12 Axial force of thrust ring under 350 Nm torque

图13 500 Nm扭矩的止推半环轴向力Fig. 13 Axial force of thrust ring under 500 Nm torque

表4 不同扭矩下的仿真结果

4.2 不同轴向预紧力对系统动态特性的影响分析

图14～18为系统在3种不同轴向预紧力工况下的动态特性结果。结果表明，系统启动阶段，止动轮毂由过渡圆弧段爬坡到工作斜面段过程中，止动轮毂轴向冲击力波动较大,在6 000，7 000和8 000 N轴向预紧力工况下的冲击力峰值分别可达28.56，29.21，30.6 kN；在爬坡到工作斜面稳定后，其轴向力波动很小，分别稳定在12.38，12.42和12.6 kN左右。止推半环所受轴向冲击力趋势与止动轮毂轴向力趋势相似，在6 000，7 000和8 000 N轴向预紧力工况下，止推半环轴向力冲击峰值分别可达8.36 kN/8.04 kN、8.63 kN/8.02 kN和9.34 kN/8.35 kN；止动轮毂轴向位移则在止动轮毂爬坡到工作斜面后分别稳定在4.19，3.63和3.24 mm。

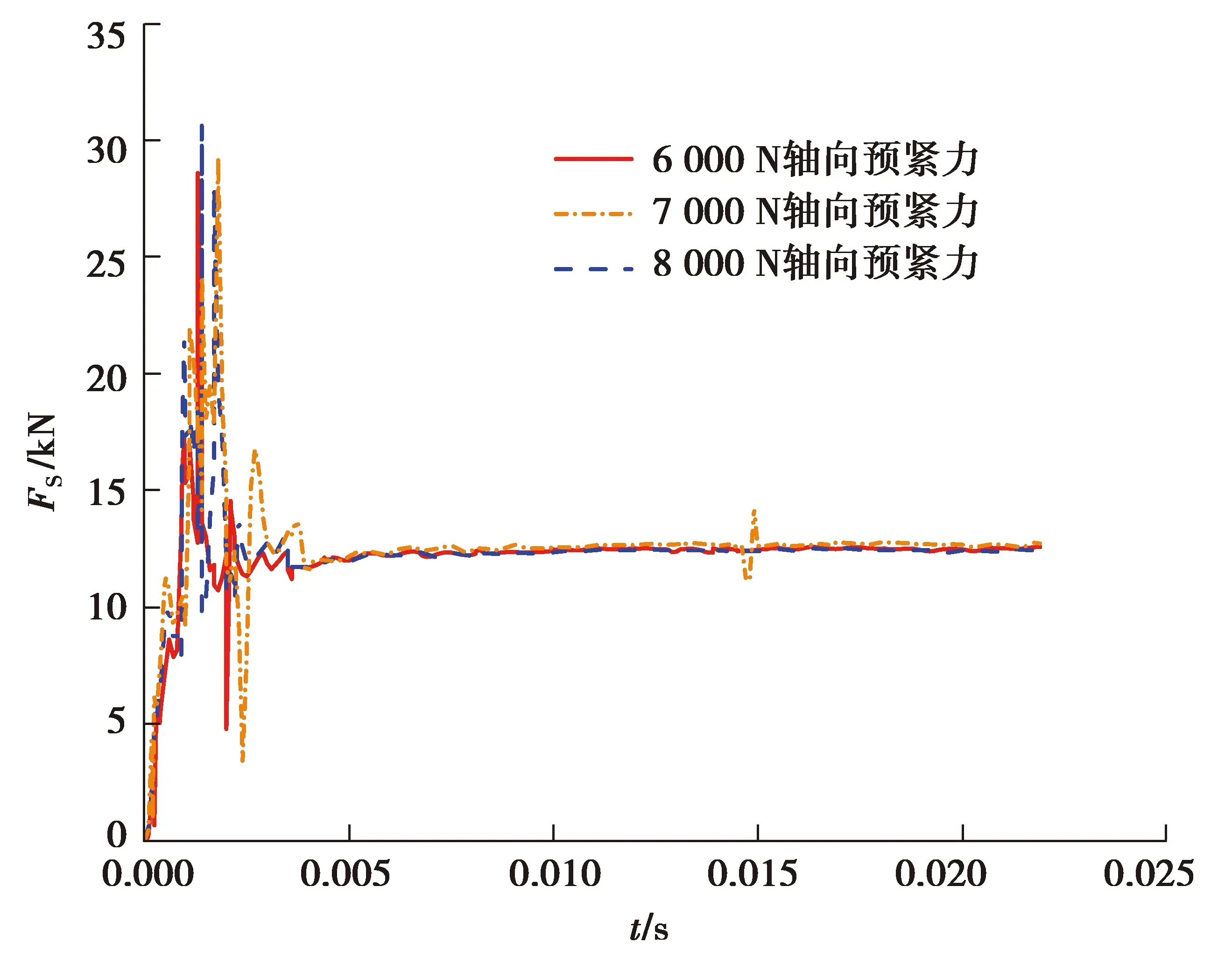
图14 不同轴向预紧力下的止动轮毂轴向力Fig. 14 Axial force of doghub under different axial preloads

图15 不同轴向预紧力下的止动轮毂轴向位移Fig. 15 Axial displacement of doghub under different axial preloads

图16 6 000 N轴向预紧力下的止推半环轴向力Fig. 16 Axial force of thrust ring under 6 000 N axial preload

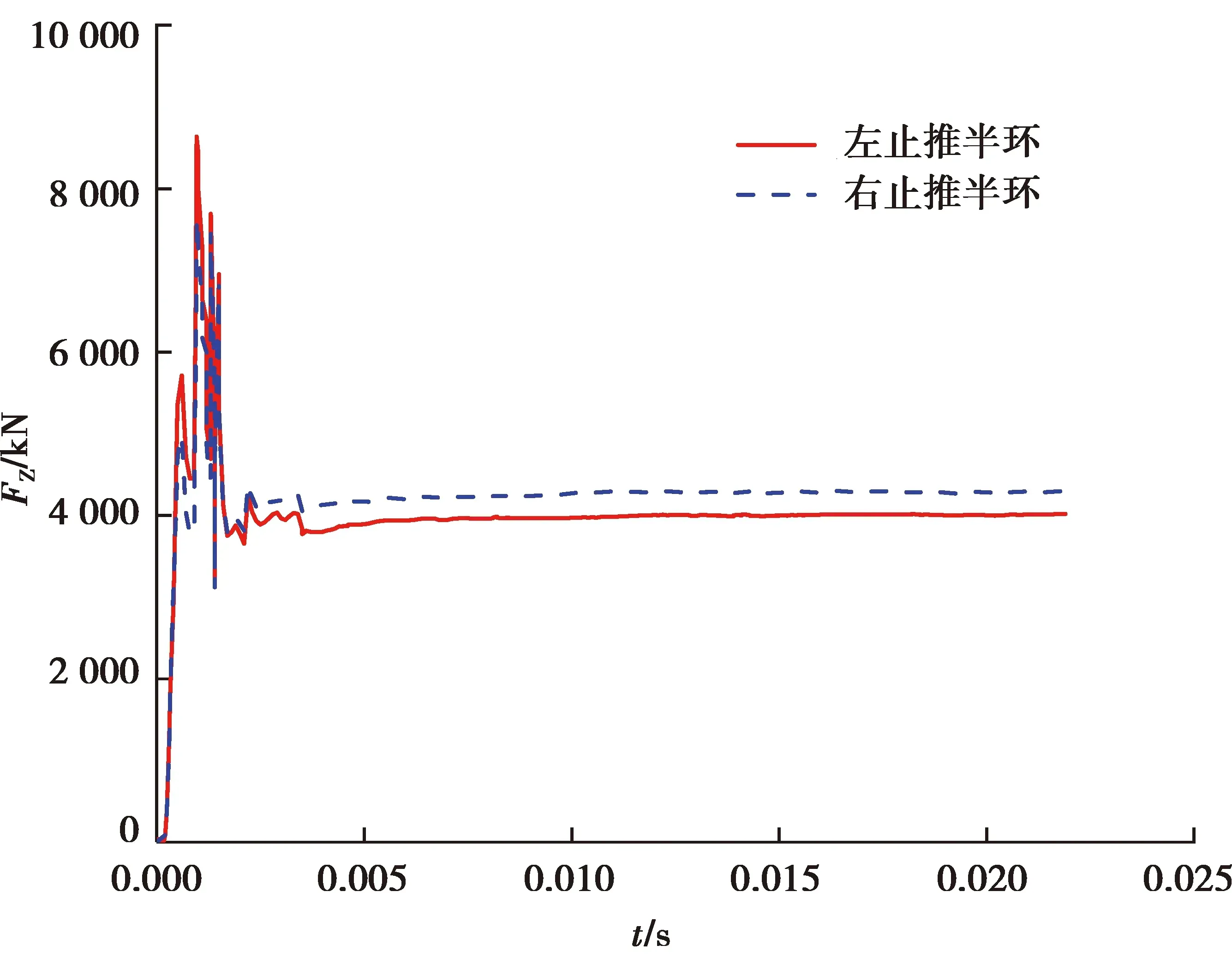
图17 7 000 N轴向预紧力下的止推半环轴向力Fig. 17 Axial force of thrust ring under 7 000 N axial preload

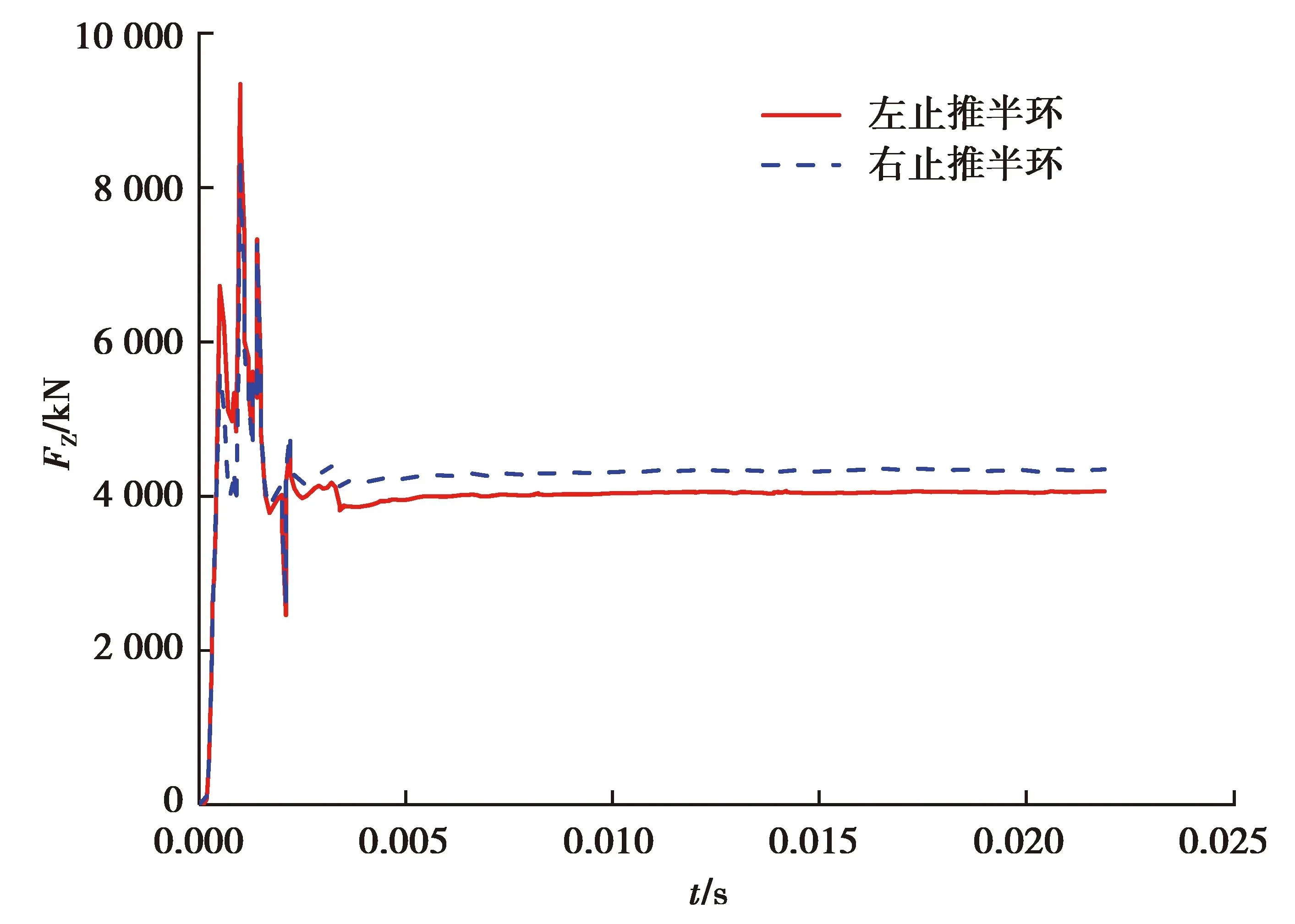
图18 8 000 N轴向预紧力下的止推半环轴向力Fig.18 Axial force of thrust ring under 8 000 N axial preload

对比6 000，7 000和8 000 N 3种不同轴向预紧力下的仿真结果如表5所示。

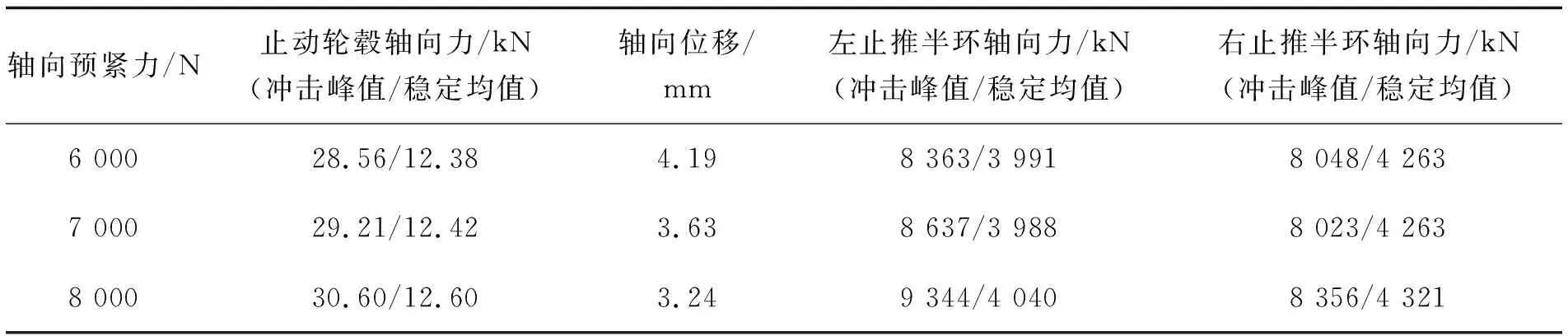
表5 不同轴向预紧力下的仿真结果

从表中可以看出，轴向预紧力由6 000 N逐步增大到8 000 N，止动轮毂轴向力有所增大，系统启动爬坡阶段的轴向冲击峰值由28.56 kN增大到30.60 kN，爬坡到工作斜面稳定后的均值由12.38 kN增大到12.60 kN；止推半环所受轴向冲击力趋势与止动轮毂轴向力相似，止推半环所受轴向冲击力也明显随着轴向力的增大而增大，冲击峰值由8.30 kN/8.00 kN增大到9.30 kN/8.30 kN，均值由3.99 kN/4.26 kN增大到4.04 kN/4.32 kN。止动轮毂轴向位移则明显减小，由4.19 mm减小到3.24 mm；所以，相对于额定8 000 N轴向预紧力，适当减小轴向预紧力能一定程度上减小系统所受轴向冲击力。

5 结 论

在分析发动机止动轮毂系统工作原理的基础上，提出了止动轮毂三爪曲面接触系统动力学建模与分析方法，研究了不同扭矩和轴向预紧力工况对止动轮毂系统轴向冲击力与位移的影响规律，主要结论如下:

1)在止动轮毂由过渡圆弧段爬坡到工作斜面过程中，止动轮毂与止推半环所受轴向力波动较大且会达到峰值；在止动轮毂爬坡完稳定在工作斜面转动后，止动轮毂与止推半环所受轴向力波动很小，基本趋于稳定。

3)随着轴向预紧力增大，止动轮毂轴向力与止推半环所受轴向力在系统启动阶段与稳定阶段都有所增大，止动轮毂轴向位移则明显减小。因此适当减小轴向预紧力能一定程度上减小系统所受轴向振动冲击。