RV摆线轮专用镗床几何误差分析

陈佳豪，陈永洪，肖 向，陈兵奎

(重庆大学 机械传动国家重点实验室 重庆 400044)

RV减速器作为一种刚性好、可靠性高、精度高、效率高的新型两级传动机构，被广泛运用于数控机床等高精密设备中[1-2]。摆线轮是RV减速器中的核心零件，其坐标孔尺寸精度及形位公差均要求极高[3]，其加工质量对精密机械装备的性能具有重要影响[4]。目前，日本Nabtesco(原帝人)公司RV减速器关键零件的加工均采用高精度专用机床，加工精度高，产品一致性和稳定性好。国内高精度RV减速器的产业化起步较晚，缺少先进的设计理论与方法。国内RV减速器摆线轮坐标孔的常规加工设备为进口的高精度坐标磨床、高精度坐标镗床等通用设备[5]。

影响机床加工精度的主要误差源有机床热误差和几何误差。自1960年代，国内外学者就开始对机床的误差模型进行研究，如今机床误差建模技术已经相当成熟，目前机床误差建模理论中比较有代表性的建模方法有基于刚体动力学理论的方法和齐次坐标变换法等。Ferreira等[6]基于刚体运动学理论，建立了三轴机床几何误差模型，为几何误差研究奠定了基础；Soons等[7]基于刚体假设推导出有多个直线轴、旋转轴的数控机床空间误差模型；Okafor等[8]基于齐次坐标变换理论建立了几何误差和热误差的综合误差模型；陈国达等[9]根据刚体动力学和齐次坐标变换理论，建立了RTTTR结构的五轴机床误差模型，并对模型中37项几何误差元素进行了灵敏度分析。

目前还没有从机床几何误差的角度针对摆线轮坐标孔镗孔机床进行研究的报道[10-14]。针对普通摆线轮镗孔设备存在效率低、精度低等问题，本研究中设计了一种摆线轮坐标孔专用镗床，重点研究了机床的总体结构，基于多体系统理论与齐次坐标变换建立了专机几何误差模型，在此基础上，利用灵敏度分析法对各个几何误差的灵敏度进行分析，并结合灵敏度分析结果，进一步对机床关键部件进行选型。

1 专用镗床结构设计

由于RV减速器摆线轮坐标孔的精度要求比中心孔更高，镗孔工序采用粗镗—半精镗—精镗的方式[15]。针对摆线轮坐标孔精镗加工设计一款专用镗床，其整体结构如图1所示。

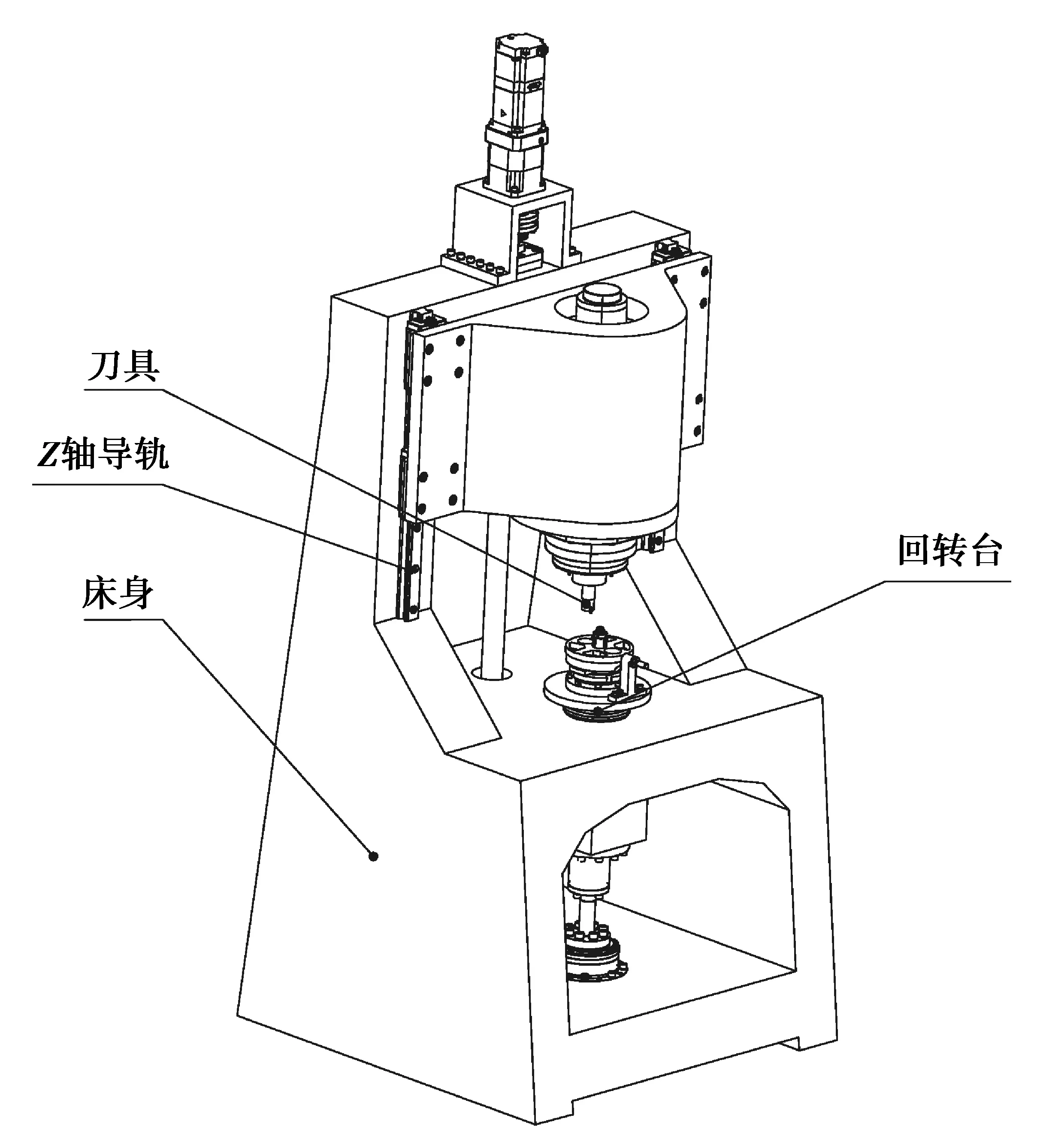
图1 摆线轮坐标孔专用镗床整体结构Fig. 1 Structure of the special boring machine for cycloid wheel

机床床身采用龙门式结构，其刚性好，结构简单，有利于提高产品的制造精度[16]。本专用镗床具有刀具垂直移动、刀具绕自身主轴的转动和分度转台的转动3个运动，机床结构简单，传动链短，其结构简图和坐标系如图2(a)所示。

图2 专用镗床示意图Fig. 2 Diagram of the special boring machine

为了运用多体系统理论建立专机的几何误差模型，需要确定各个部件的静止变换矩阵和运动变换矩阵。因此首先需要建立各部件对应的坐标系，其中床身坐标系O0-X0Y0Z0为机床固定坐标系，其原点位于摆线轮零件中心孔，X0轴指向坐标孔中心线，Z0轴与C轴初始状态重合。图2(b)为本专用机床的拓扑结构。为简化误差模型以方便误差的计算，设置的局部坐标系应尽可能地重合，将刀具坐标系O6-X6Y6Z6的坐标原点O6设置在刀具中心点，距离O0的垂直距离为H，平行于X0轴向的水平距离为K，坐标轴与床身坐标系O0-X0Y0Z0平行；将主轴坐标系O5-X5Y5Z5和Z轴坐标系O4-X4Y4Z4设置与刀具坐标系O6-X6Y6Z6重合；将机床其余结构的坐标系原点都设置与机床固定坐标系O0-X0Y0Z0重合。

2 专用镗床几何误差建模

2.1 几何误差元素分析

根据图2，专用镗床拥有Z轴1个移动副和C轴1个转动副，根据机床多体系统理论[13]，专用镗床的几何误差元素如图3所示，图中O4-X4Y4Z4为Z轴坐标系，O1-X1Y1Z1为C轴坐标系。

图3 专用镗床几何误差元素分析Fig. 3 Geometric error element analysis of the special boring machine

专机的Z轴移动副存在3个平动误差，分别是沿X轴方向的平动误差δzx、沿Y轴方向的平动误差δzy和沿Z轴方向的平动误差δzz，以及3个转动误差，分别是绕X轴转动的转动误差θzx、绕Y轴转动的转动误差θzy和绕Z轴转动的转动误差θzz。旋转副C轴和移动副类似，将会产生相对于理想位置的X、Y、Z3个方向的平动误差和转动误差，分别是δcx、δcy、δxz、θcx、θcy、θcz这6项几何误差。本专用镗床的误差元素除了移动副与旋转副的6项几何误差元素之外，还包括了Z轴与C轴的平行度误差βzz。平行度误差βzz可分解为床身坐标系O0-X0Y0Z0中X0轴和Y0轴方向上的转动误差，为了与运动副的转动误差相区别，将其定义为垂直度误差βzx和βzy。此外还存在刀具的安装误差，刀具在安装时存在6个自由度，因此也会分别产生δdx、δdy、δdz3个平动误差以及θdx、θdy、θdz3个转动误差共6项几何误差。专用镗床的综合几何误差元素如表1所示，共计20项。

表1 专用镗床综合几何误差元素

2.2 专用数控镗床几何误差建模

2.2.1 坐标变换矩阵

假设高序体m在初始阶段其坐标系与低序体n的坐标系重合，那么高序体相对于低序体的任意平移运动都可以看作是坐标原点分别沿着其X、Y、Z轴做平移运动的结果，任意旋转运动都可以看作是坐标系分别绕着其X、Y、Z轴做旋转运动的结果[17]。

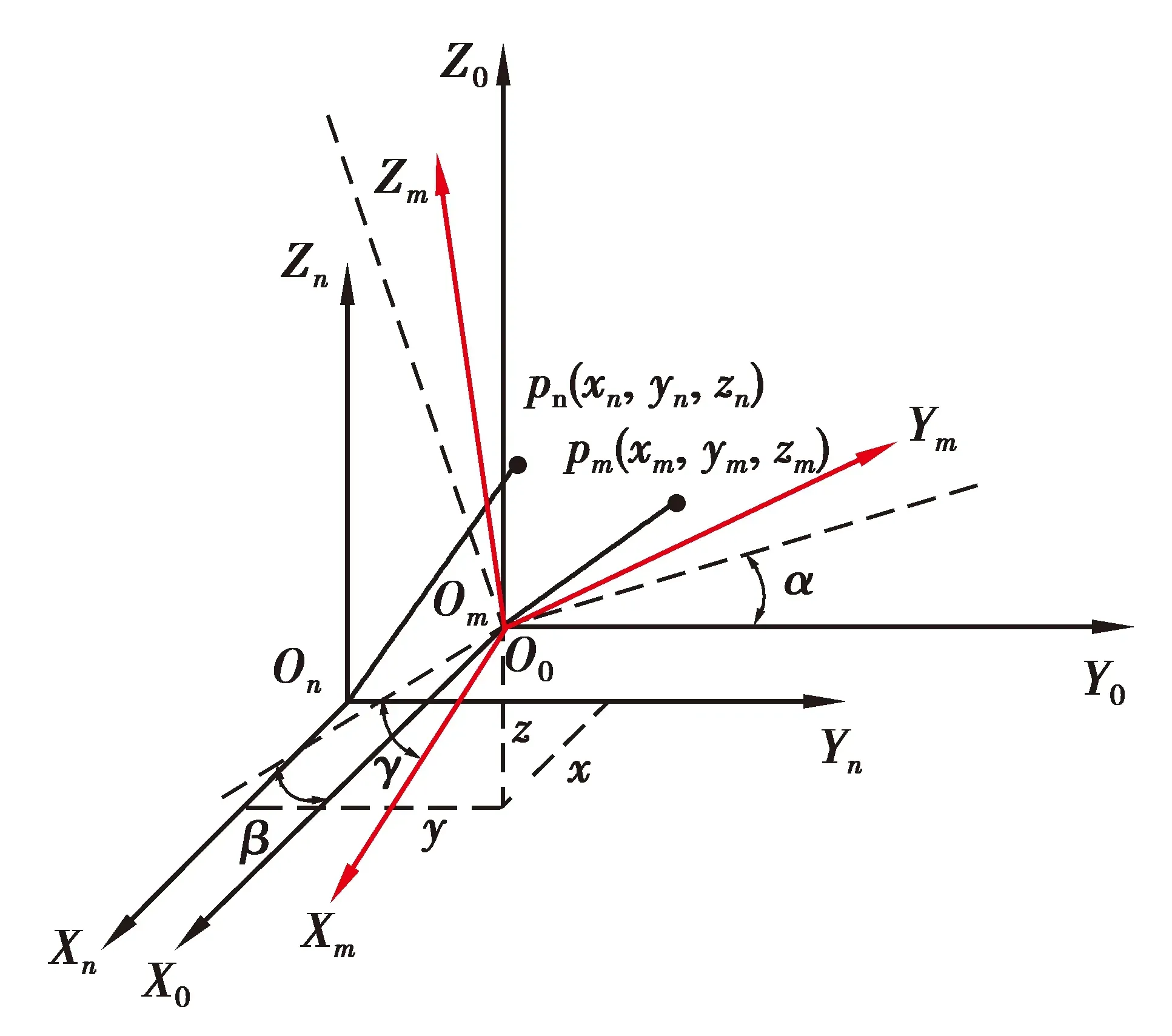
图4 坐标变换示意图Fig. 4 Schematic diagram of coordinate transformation

(1)

2.2.2 专用镗床几何误差模型建立

在上一节中分析了专用镗床各个运动副的误差元素，刀具的6项几何误差为安装误差，属于静止误差，Z轴的垂直度误差也为静止误差，专用镗床各相邻体之间的静止变换矩阵如表2所示，各相邻体之间的运动变换矩阵如表3所示，其中I4×4表示单位矩阵。

表2 专用镗床静止变换矩阵

表3 专用镗床运动变换矩阵

上标e表示实际变换矩阵，上标i表示理想变换矩阵。在实际加工中，零件3与工作台2之间采用高精度夹具连接，不考虑夹具的定位误差，因此，零件3的坐标系O3-X3Y3Z3到工作台2的坐标系O2-X2Y2Z2的理想和实际变换矩阵均为单位阵，同理，工作台2与C轴1，主轴5与Z轴4之间的理想和实际变换矩阵也都是单位阵，即：

(2)

因此，刀具坐标系O6-X6Y6Z6到工件坐标系O0-X0Y0Z0的理想与实际变换矩阵为：

(4)

刀具坐标系O6-X6Y6Z6上点P0(xd,yd,zd)，理想情况下在工件坐标系O0-X0Y0Z0下的坐标与实际情况下在工件坐标系O0-X0Y0Z0下的坐标之差便是专用机床的综合几何误差模型R，满足如下关系：

3 专机灵敏度分析及关键部件选型

3.1 模型实例计算与验证

摆线轮以及专机的相关参数如表5所示，刀具中心起始点位置在刀具坐标系下的理想坐标为P0(0,0,0)，由于存在几何误差元素，实际刀具加工时与摆线轮接触点的位置在零件坐标系下为P1(a,b,c)，如图5所示，根据式(5)，P1与P0应满足如下关系：

(5)

表4 专用镗床综合变换矩阵

表5 摆线轮相关参数

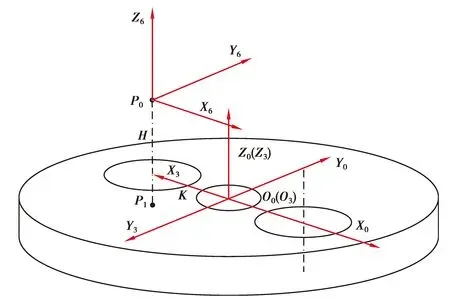
图5 摆线轮加工点位置关系Fig. 5 The position relation of cycloid gear processing points

(6)

(7)

假设其余几何误差元素为零，图6为C轴Y向转动误差θcy对专机加工精度的影响分析，虚线为摆线轮理想状态，由于存在Y向转动误差θcy，实线为摆线轮的实际状态，坐标孔的实际中心线与理论中心线存在一个角度为θcy的夹角，当刀具进给到某一点P1时，点P1到坐标孔理论中心线的距离S为坐标孔在该点的误差值。

图6 θcy影响分析Fig. 6 The impact analysis of θcy

根据图6，基于小误差假设，利用三角关系法可得坐标孔在加工过程中的误差为:

(8)

图7 θcx、θcz、δcx、δcy影响分析Fig. 7 The impact analysis of θcx,θcz, δcx and δcy

(9)

表6 两种方法的误差对比

由表6可知，本文的RV摆线轮坐标孔专用镗床的几何误差模型的计算结果与三角关系法的计算结果吻合较好，验证了所建几何误差模型的正确性。

3.2 几何误差元素灵敏度分析

专用机床的几何误差模型可用于分析专机各个几何误差的灵敏度，目前求解灵敏度的方法主要有直接法、高阶灵敏度函数法和一阶灵敏度函数法。直接法与高阶灵敏度函数法计算量较大、求解困难且实用性较低[15]，因此本研究中采用一阶灵敏度函数法对专机各个几何误差进行灵敏度分析。RV摆线轮坐标孔专用镗床的几何误差模型包含20个几何误差元素，为了得到各几何误差元素对最终专机加工精度的影响程度，需要对各误差元素进行灵敏度分析。根据前面得到的几何误差模型，它可以表示为20个几何误差元素的函数，形式如下：

(10)

(11)

式中：l=z,c；k=x,y,z；不同的几何误差元素对专机加工精度的影响程度不同，本文中采用对误差模型求各几何误差元素偏导数的方法，得到误差参数的灵敏度表达式：

(12)

(13)

由于部分几何误差元素的灵敏度与刀具进给量z有关，因此，各几何误差元素的灵敏度系数都与刀具进给量z相关，在200～212 mm的范围内，z每增加1 mm取一个点，共选取13个点对各个几何误差元素的X、Y向灵敏度系数进行分析。

图8为各个几何误差元素在X方向的灵敏度系数随着刀具进给的变化规律。由图可知，影响专机X向误差的主要几何误差元素为δzx、θcy、βzy、δcx、δdx，其余几何误差元素的灵敏度系数均为零，并且随着刀具进给，δdx、δcx、δzx的灵敏度系数逐渐降低，θcy、βzy的灵敏度系数逐渐升高；在z=201 mm时，所有几何误差元素的灵敏度系数基本相等，之后θcy、βzy的灵敏度系数不断增大，δdx、δcx、δzx的灵敏度系数不断减小；在z=212 mm时，θcy、βzy的灵敏度系数占了X向总灵敏度系数的近90%，其余几何误差元素的灵敏度系数只占10%。因此，影响X方向误差的关键几何误差元素为θcy、βzy。

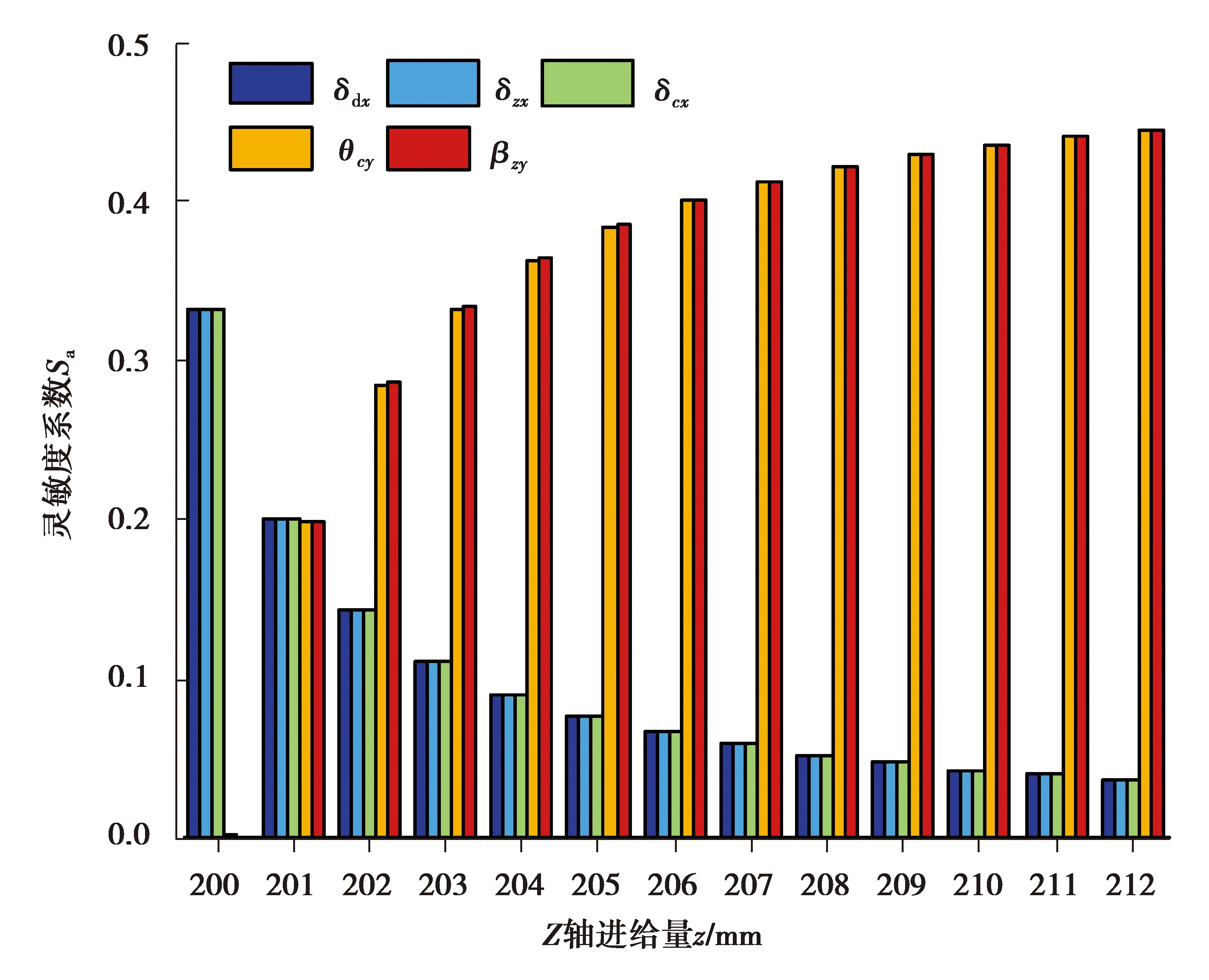
图8 误差元素X向灵敏度系数分析Fig. 8 Analysis of sensitivity coefficient of X-axis error elements

图9为各个几何误差元素在Y方向的灵敏度系数随着刀具进给的变化规律。由图可知，影响专机Y向误差的主要几何误差元素为δzy、θcx、βzx、θcz、δcy、δdy，其余几何误差元素的灵敏度系数均为零。随着刀具进给，θcz对专机加工精度的灵敏度系数逐渐降低，δdy、δcy、δzy的灵敏度系数基本保持不变，θcx、βzx的灵敏度系数逐渐增大，但θcz的灵敏度系数总是远大于其余几何误差元素的灵敏度系数；在z=200 mm时，θcz的灵敏度系数占了Y向总灵敏度系数的90%以上，其余误差元素只占不到10%；在z=212 mm时，θcz的灵敏度系数占了Y向总灵敏度系数的60%以上，其余误差元素只占不到40%。因此，影响Y方向误差的关键几何误差元素为θcz，其次是θcx、βzx。

图9 误差元素Y向灵敏度系数分析Fig. 9 Analysis of sensitivity coefficient of Y-axis error elements

综上所述，影响专机加工精度的主要几何误差元素有11项，表7所示为专用机床各个误差元素对专机精度影响分类。

表7 几何误差的影响分类

为了更好地表达上述11项几何误差元素对专机加工精度的影响程度，引入几何误差综合灵敏度系数Sv，对各几何误差元素的X、Y向灵敏度进行归一化处理。综合灵敏度系数的表达式为：

(14)

图10为各个几何误差元素的综合灵敏度系数随刀具进给的变化规律，其中黄色棱柱表示θcz的灵敏度系数，其余颜色的棱柱表示其余10项对专机精度有影响的几何误差元素的灵敏度系数。由图可知，在刀具进给量z=200 mm，即刀具最初接触工件时，θcz的灵敏度系数最大，最大值为85%，随着刀具进给，θcz的灵敏度系数逐渐减小，在刀具进给量z=212 mm，即刀具对工件完成加工时，θcz的灵敏度系数达到最小值45%，θcz的灵敏度系数一直明显大于其余几何误差元素的灵敏度系数。因此，对专用机床的精度影响最大的几何误差元素为C轴围绕其Z轴方向的转动误差θcz。

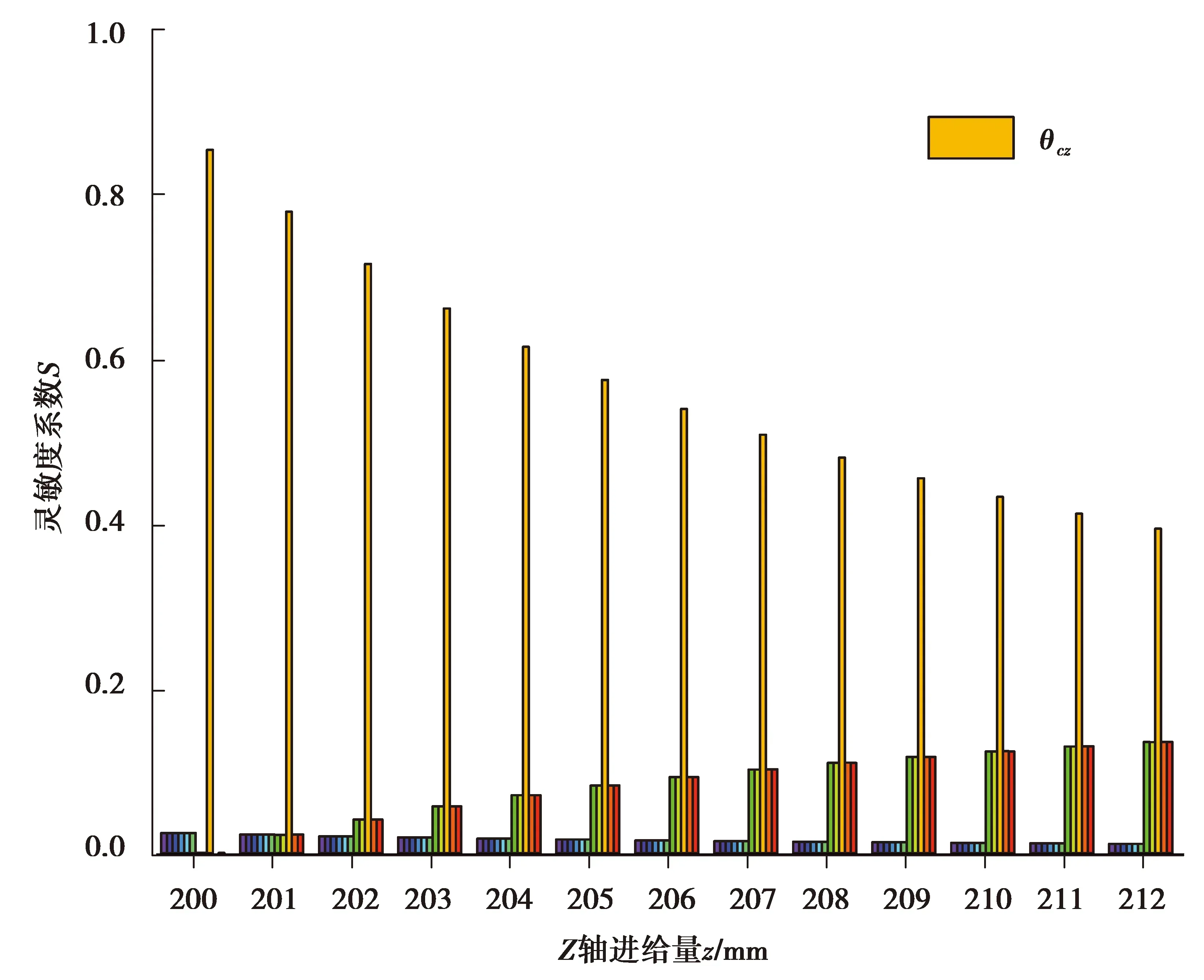
图10 误差元素综合灵敏度系数分析Fig. 10 Analysis of sensitivity coefficient of error elements

3.3 专机关键部件选型

前面分析了专用数控镗床各个几何误差元素的灵敏度系数，θcz对零件的加工精度影响最大，因此，在设计专用镗床结构时，应重点控制θcz这一几何误差元素。减小机床加工误差的方法有误差防止法和误差补偿法，由于本专用镗床自由度较少，无法自动补偿，因此采用误差防止法，可在结构上尽量减少几何误差的产生。

旋转轴C轴作为回转工作台，工件的分度采用基于高精度端齿盘结构的专用转台，端齿盘零件图如图11所示，端齿盘的分度精度高，且结构简单，价格便宜，端齿盘在进行分度时，其分度精度可达2″[18]，即θcz≤9.7 μrad，端齿盘与工件之间用高精度夹具体连接，其回转精度可直接反映在工件上，不考虑其他几何误差的影响时，带入式(6)和(7)可得其造成的误差低于0.34 μm。

图11 端齿盘零件图Fig. 11 The structure of the end-tooth disc

五轴机床的综合误差模型中包括了37个误差项[19]，测量和补偿难度都较大，并且成本较高。本专用镗床去除五轴机床多余自由度，只保留满足零件加工工艺要求的自由度，能大幅度降低零件的生产成本，提高生产效率。

4 结 论

本文中以RV减速器摆线轮坐标孔专用镗床为研究对象，完成了专机几何误差模型建立，利用三角关系法验证了几何误差模型的可行性，分析了各个几何误差元素在专机加工过程中的灵敏度变化规律，得出如下主要结论：

1) RV摆线轮坐标孔专用镗床共有20项几何误差元素，包括移动副与旋转副的运动误差、刀具安装误差、移动副与旋转副垂直度误差；

2)基于小误差假设，δzx、θzy、θcy、βzy、δcx在X方向影响专机加工精度，θzx、δzy、θzz、θcx、βzx、θcz、δcy在Y方向影响专机加工精度，其余几何误差元素不影响专机加工精度。

3)各个几何误差元素中，θcz对专用机床精度影响最大，随着刀具的进给，θcz的影响程度逐渐减小，刀具最初接触工件时，θcz灵敏度系数最大为85%，刀具对工件完成加工时，θcz灵敏度系数最小为45%。

4)采用误差防止法尽量减小θcz，方法为C轴选用精密端齿盘进行分度，其分度精度可达2″，即θcz≤9.7 μrad，不考虑其他几何误差的影响时，理论上θcz造成的误差低于0.34 μm。