冲击荷载下煤的动力学特性实验研究

陈 军 张文清

（1.淮河能源控股集团潘二煤矿，安徽 淮南 232000；2.安徽理工大学安全科学与工程学院，安徽 淮南 232001）

目前，国内外学者对煤岩受载荷变形破裂过程中的力学性质研究中静载荷的较多，动载较少。而材料在静载与动载破坏时往往表现出不同的破坏形式和力学特征。在煤与瓦斯突出和冲击地压灾害发生初期，煤矿开采的石门揭煤、爆破掘进等会使煤体承受强烈的冲击载荷，因此，有必要研究煤岩体在瞬间冲击破坏时表现出的动力学特性。

从现有的文献资料看，对岩石类材料、混凝土、金属材料等的动态力学性能的研究较多，例如中南大学的李夕兵课题组，而针对煤岩的研究相对较少。20世纪80年代起，Klepaczko、刘宝琛、吴绵拔等人开始对煤岩的动态变形特性进行相关研究。近年，单仁亮、刘晓辉等人分别从煤岩的动态强度及本构关系、动态能量耗散等方面开展研究，取得了一定成果。

该文利用分离式霍普金森压杆装置（简称SHPB）对煤岩进行不同载荷作用下的冲击压缩实验，研究煤岩的动态抗压强度、弹性模量等力学性能参数及其与应变率的关系，为防治矿山动力学灾害提供理论依据。

1 煤岩试件的制备

该实验选用的煤岩取自淮南矿业集团张集煤矿C煤层。将大煤块运达学校后，在安徽理工大学岩石试件加工实验室钻取加工成直径为50mm的圆柱形试件，试件的长径比控制在0.5~1.0。同时，将试件的两端用砂纸仔细打磨，保证2个端面应该有足够的光洁度以减少实验过程中端面摩擦的影响。2个端面的平行度在0.01mm以上，以满足SHPB实验要求。制作完成的试件如图1所示。

图1 煤岩试件实拍图

2 动态冲击实验

2.1 SHPB装置基本原理

该实验是在安徽理工大学冲击实验室的75mmSHPB实验系统上完成的，装置示意如图2所示。系统采用的撞击杆（即子弹）、入射杆、输出杆直径均为75mm，长度分别为0.4m、4m和2.5m，材质均为高强度合金钢，弹性模量为195GPa。

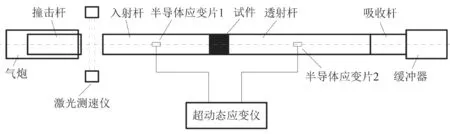
图2 分离式霍普金森压杆系统示意图

用高压气体驱动子弹以一定的速度撞击输入杆，在输入杆内产生一个应力脉冲ε（），称为入射波。入射波沿输入杆向试样传播，经过应变计1被记录下来。当入射波传播到试样位置时，推动试样开始变形，并在输入杆中产生一个反向应力脉冲，称为反射波ε（），到达应变计1时也被记录下来。另一部分脉冲透过试样进入输出杆向前传播，称为透射波ε（），经过应变计2时被记录下来。

基于一维弹性应力波和应力均匀性假设的条件下，试样的平均应力、平均应变和平均应变率可用公式（1）计算。

式中：为平均应力；为平均应变；为平均应变率；为压杆的弹性模量；为应力波在压杆中的弹性波速，本系统为4984m/s；和分别为压杆和试件的横截面积；为试件的长度；ε（）和ε（）分别为透射波和反射波对应的应变。

2.2 实验过程简介

该实验共完成8个煤岩试件的冲击实验，驱动气压控制为0.2MPa~0.4MPa，子弹冲击速度为4.368m/s~6.153m/s，其中成功取得有效数据的试件6个，其实验情况统计见表1。

表1 煤岩动态冲击实验情况汇总

通过调整驱动气压，实现以不同的子弹速度撞击入射杆，给试件施加不同强度的动载荷。随着驱动气压增大，子弹速度提高，荷载强度越大，试件的应变率也增大。收集不同荷载冲击后煤岩试件的碎块如图3所示。

图3 冲击后的试件

1、3、4、5、7和8试件对应的实验应变率分别为96s、120s、125s、145s、177s和 186s。宏观上分析，在96～186s应变率范围内，煤体均处于破碎状态，但未被完全破碎成粉末状，这可能与原煤试件的脆性破坏有关。随着应变率的提高，煤体破碎程度加剧。

3 煤岩动态力学性能分析

3.1 动态力学参数

实验得到的不同冲击速度下，煤岩试件的动态抗压强度、峰值应变、动态弹性模量等动态力学参数如表2所示。

表2 煤岩动态力学参数

3.2 动态应力应变曲线

图4为不同应变率条件下的煤岩动态应力应变曲线。可以看出，不同应变率条件下煤岩的动态抗压强度和动态弹性模量不同，均随着应变率的提高而增大。

图4 煤岩动态应力应变曲线

从煤岩的动态应力应变曲线整个过程来看，起始阶段由于煤岩固有的内部裂隙受压，使曲线向上弯曲上升；随后煤岩进入线弹性阶段，曲线近似为直线；当应力继续上升至峰值应力的80%时，曲线开始向下弯曲，试件内部开始破坏；直至峰值应力以后，试件破坏。由于在峰值应力点后，煤体迅速破坏，峰后应力应变曲线全部为一类卸载（负斜率），而SHPB实验技术对峰后一类卸载曲线的测量尚存争议。因此，煤岩的整个变形过程基本包括了密实阶段、弹性变形阶段、屈服阶段和破坏阶段。

3.3 应变率效应分析

将煤岩在不同应变率条件下的动态抗压强度数据描绘在同一坐标中，如图5所示。

图5 煤岩动态抗压强度与应变率的关系

实验结果表明，在90s~200s的应变率范围内，随着应变率的增大，煤岩的动态抗压强度显著提高，体现了明显的应变率效应。利用指数函数拟合得到了较好的效果。

在该实验应变率范围内，煤体的动态强度较静态强度提高了约2倍~5倍，煤是率敏感性材料，具有应变率强化的特点。这是因为煤体的破坏是因为裂纹的产生与发展，而裂纹形成所需的能量远比裂纹发展所需要的能量高，当加载速率较高时，产生裂缝的数量就多，荷载作用于试件的时间比较短，材料没有足够的时间用于能量的积聚时，它只有通过提高应力的方法来达到提高能量的目的，结果导致材料的破坏强度随应变率的提高而增加。

在实验应变范围内，峰值应变也具有明显的应变率效应，体现出显著的动态增韧效果。随着应变率的增大，煤岩的峰值应变近似呈指数增长。

4 冲击破坏的能量分析

由文献[1]可知，在SHPB实验系统中应力波（）所携带的能量通过式（2）计算得到。

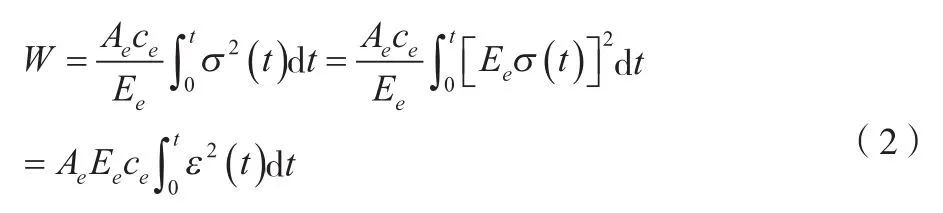
式中：为应力波携带的能量；A为输入与输出杆的横截面积；E为输入与输出杆材料的弹性模量；C为一维应力波速度；（）为应力波对应的应力；（）为应力波对应的应变。

那么，根据计算的入射波、反射波和透射波能量，试件的耗散能如公式（3）所示。

式中：W为应力波的入射波能量；W为反射波能量；W为透射波能量；W为试件的耗散能。

计算煤岩试件在不同强度冲击载荷作用下的能量耗散结果汇总于表3。

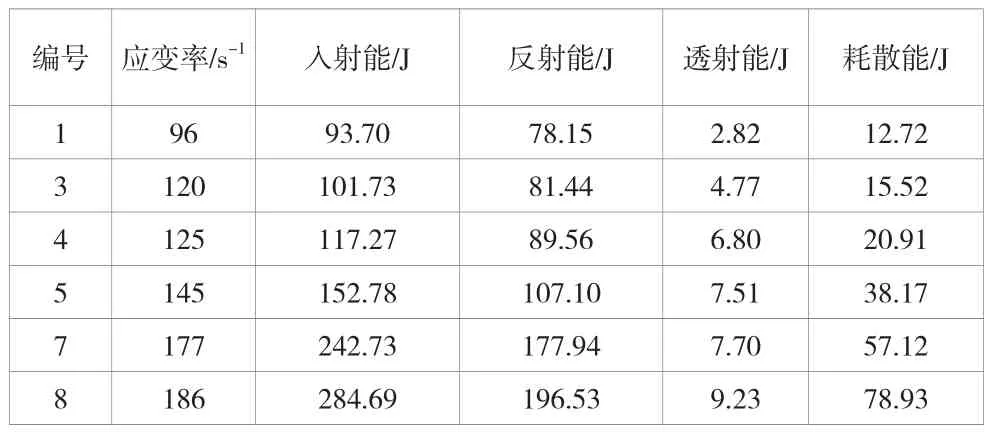
表3 煤岩冲击载荷作用下能量计算结果

由表3可知，随着应变率的提高，应力波携带的入射能、反射能、透射能以及耗散能等能均呈增加的趋势。

图6是不同载荷作用下的耗散能随实验应变率的变化规律。可以看出，随着应变率的提高，应力波携带的能量呈线性增长。而试件破坏吸收的耗散能，呈指数增长，即随着应变率的提高，用于试件破碎的能量快速增加，呈现明显的应变率相关性。这与前人对岩石在动态冲击作用下的能量耗散规律研究基本一致。

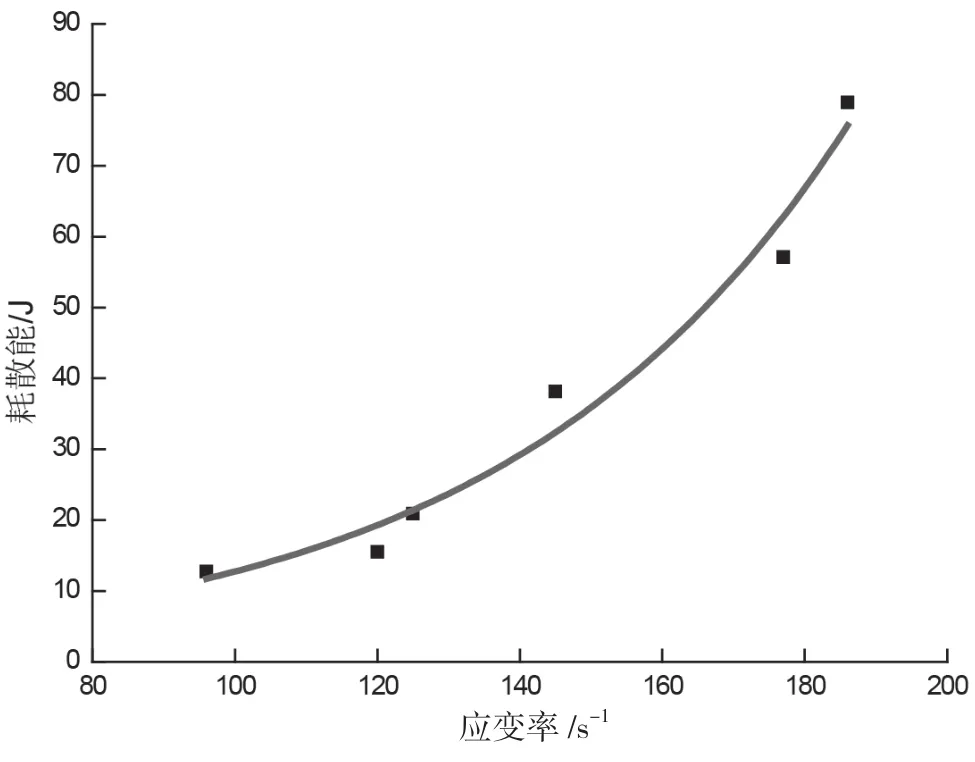
图6 耗散能与应变率的关系

5 结论

煤岩的动态变形过程与静态破坏过程基本相似，都包括密实阶段、弹性变形阶段、屈服阶段和破坏阶段。煤岩的动态弹性模量随应变率的提高而增大，煤岩在达到峰值应力前具有较好的线弹性变形特性。动态抗压强度具有显著的应变率依赖性，随应变率的增大呈近似指数增长。冲击载荷作用下，煤岩破碎的耗散能呈明显应变率相关性。随着应变率的提高，耗散能呈指数增长，说明用于试件破碎的能量快速增加。受实验样本数量的限制，煤岩在较低和较高应变率条件下的动态力学特性有待进一步实验研究。