基于遗传算法的对空射击有利度分析

吕杰杰，王炳华，高延龙

（炮兵防空兵学院郑州校区，郑州 450000）

0 引言

对空射击有利度是表征某防空火力单元对空中目标射击的有效性指标，可以认为是火力单元对空中目标实施抗击的综合毁歼概率，是防空兵部队进行火力分配的重要参考因素。该指标体现的是某火力单元相较于其他火力单元对空中目标进行抗击的有利程度，是一个相对值，并非绝对值。由于战场的随机性和影响有利度的部分因素无法精确量化，故有利度也只能是概率意义上的估计和近似。

当前，对空射击有利度分析主要有两种方法：一种是采取固定空中目标，分析各火力单元的方式，如对01 批目标，有5 个火力单元能够射击，通过建模分析哪个火力单元对该目标射击更加有利；另一种是采取固定火力单元，分析空中目标的方式，如在1 号火力单元射击范围内有5 个目标可以射击，通过建模分析该火力单元射击哪个目标更加有利。第1 种观点简洁直观，便于分配火力，但是容易出现任务分配不均衡，个别火力单元负担过重的情况；第2 种观点空中目标只要进入火力单元射击范围，即可得到有效处理，便于发扬火力但不利于分配火力，容易出现多个火力单元同时打击一个目标的情况。本文采取第1 种观点，理由主要有以下几点：1）目前防空兵部队的武器装备有了质的飞跃，命中率和作战范围大幅提升，不再需要靠火力集中来增强抗击效果；2）目前防空兵部队的火力单元数大幅增多，若采取第2 种观点，则后续火力分配比较复杂；3）以目标为中心，更符合防空兵部队精准释放、积极抗击的作战要求。

以往文献多是采取建立指标体系，确定指标权重，加权求和的方法计算出有利度的绝对值，该方法具有一定的局限性。主要体现在：忽视了有利度会随着战场环境的变化而变化，它是一个相对值，并非绝对值。本文立足于防空兵部队在一个射击周期内所处的战场环境基本一致这一基础，通过分析该时间段内目标与火力单元的关系，从而实现对火力单元射击有利度的排序，得出的结果是相对值，而不是绝对值。

1 影响射击有利度的因素分析

影响射击有利度可分为空中目标因素和火力单元因素两类。

1.1 空中目标因素

影响对空射击有利度的空中目标因素主要有：飞行速度（V）、飞行高度（H）、飞临时间（T）、航路捷径（D）、雷达截面积（RCS）。

根据防空火力单元的射击特性可以得出飞行速度（V）、飞行高度（H）、航路捷径（D）这3 个因素，对射击有利度的影响如图1 所示。

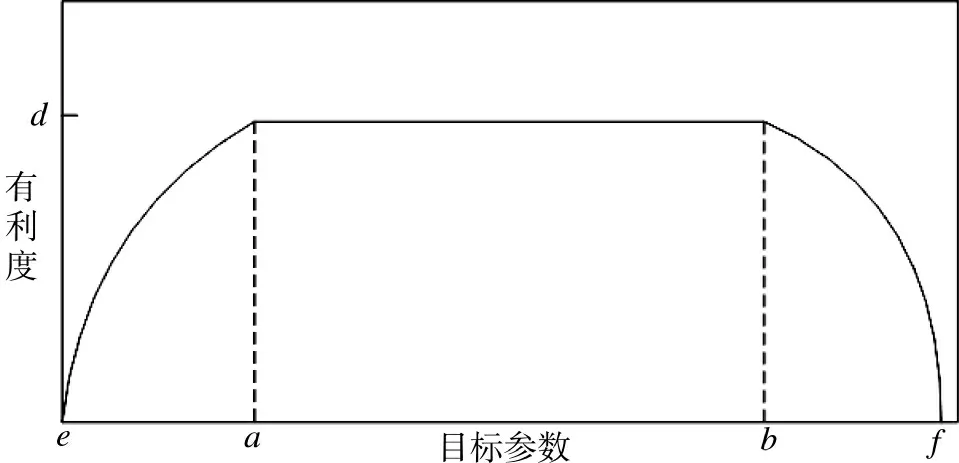
图1 飞行速度、飞行高度、航路捷径与射击有利度关系图

由图1 可知，当目标参数在a、b 区间时，有利度最高且基本保持不变；当目标参数在e、a 区间或者b、f 区间时，有利度逐渐降低；当目标参数小于e 或者大于f 时，火力单元构不成射击条件，无法射击，有利度为0。

飞临时间（T）、雷达截面积（RCS）因素对有利度的影响如图2 所示。

由图2 可知，当目标参数大于某一特定值a 时，有利度最高且基本保持不变；当目标参数在e、a 之间时，有利度逐渐降低；当目标参数小于e 时，火力单元构不成射击条件，无法射击，有利度为0。

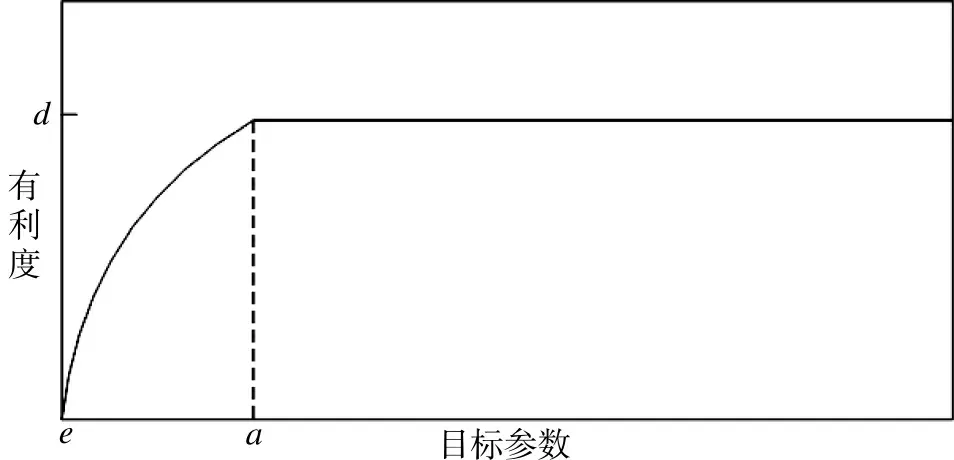
图2 飞临时间、雷达截面积与射击有利度关系图

根据上述分析，对各影响因素进行赋值计算，火力单元不同，a、b、e、f 的值也不同，需要根据各火力单元的性能指标进行确定（用M来表示该目标相对于第i 个火力单元第j 个参数的赋值）。

飞行速度（V）、飞行高度（H）、航路捷径（D）用式（1）赋值。

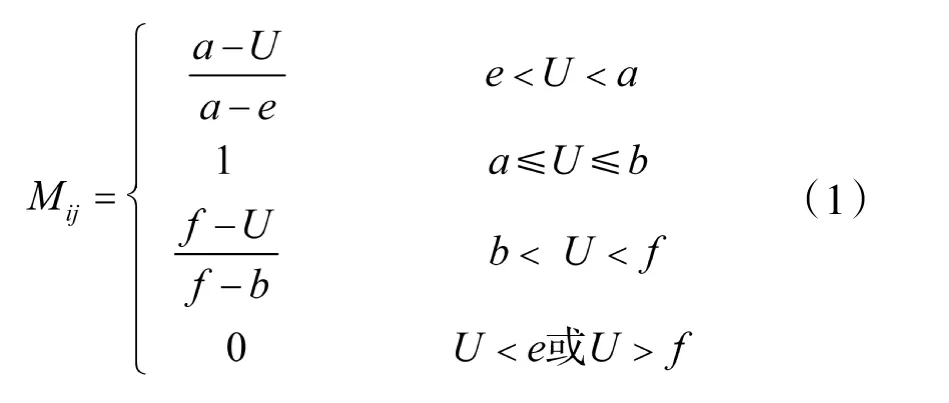
飞临时间（T）、雷达截面积（RCS）用式（2）赋值。

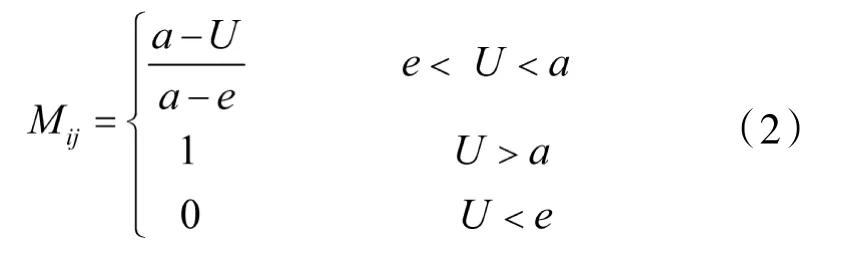
其中，U 为空中目标因素的值。

1.2 火力单元因素

影响对空射击有利度的火力单元因素主要有：命中概率（P）、最远可射击距离（Ds）、弹药可射击次数（N）、反应时间（Ty）、抗干扰能力（G）。具体影响效果为：命中概率越高，完成抗击任务的可能性就越大，射击越有利；火力单元的最远可射击距离越大，其可对敌抗击的时机就越早，射击越有利；弹药可射击次数越多，持续作战能力就越强，射击越有利；反应时间越短，灵活性就越好，射击越有利；抗干扰能力越强，性能发挥就越好，射击越有利。

通过上述分析可知，命中概率（P）、最远可射击距离（Ds）、可射击次数（N）、抗干扰能力（E）与对空射击有利度成正相关，用式（3）赋值。

反应时间（Ty）与对空射击有利度成负相关，用式（4）赋值。

其中，H表示第i 个火力单元第j 个因素的赋值结果；U表示第i 个火力单元的第j 个因素；U表示第j 个因素中的最大值；U表示第j 个因素中的最小值。

1.3 对空射击有利度模型

其中，Y为第m 个火力单元相对于第i 批空中目标的射击有利度。

2 基于遗传算法进行射击有利度计算

2.1 遗传算法基本流程

遗传算法是一种智能随机搜索算法，采取模仿自然界优胜劣汰的方式来获取最优解。按照构建初始种群，染色体选择、交叉、变异，对个体优胜劣汰的流程进行，其框图如图3 所示。

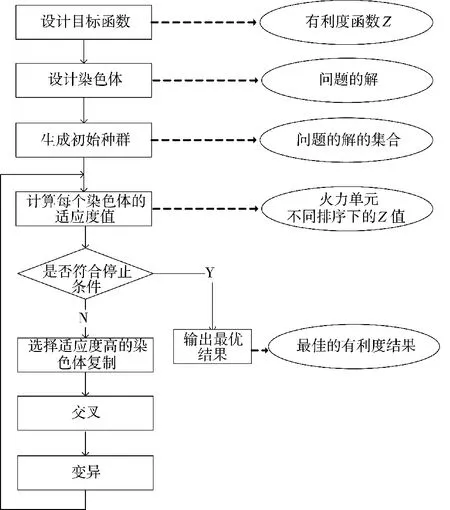
图3 遗传算法流程图

2.2 遗传算法主要参数

1）适应度函数：通常采用目标函数。

2）染色体R 的编码形式：可采取二进制编码或实数编码，用适当的形式构建所需要的解。

3）初始种群规模S：规模过小造成搜索范围过窄，难以获取最优解，规模过大造成搜索效率较低，通常取20～160 为宜。

4）选择方式：采取基于适应度“轮盘赌”的方式进行选取，可设置一定的代沟，保证每代优秀染色体向下代保留。

5）交叉方式：分为单点交叉、两点交叉和多点交叉，交叉概率过小则会导致整个算法停滞不前；交叉概率过大则会破坏种群的稳定结构，导致优秀染色体难以保留。

6）变异概率：变异概率影响着种群多样性，若其过小，则不易产生新的染色体，容易得到局部最优解而非全局最优解；若其过大，则不利于优秀染色体的保留，而将遗传算法变为单纯的搜索算法，造成结果不稳定。

3 仿真实例

某防空旅在演习中发现5 批空中目标（编号为11 批～15 批）向我飞来，在飞来方向上共部署有6 个防空火力单元（H1～H6），其中，H1～H3 为车载式防空导弹，H4、H5 为自行高炮，H6 为便携式防空导弹。目标信息和火力单元性能参数如表1、下页表2所示。

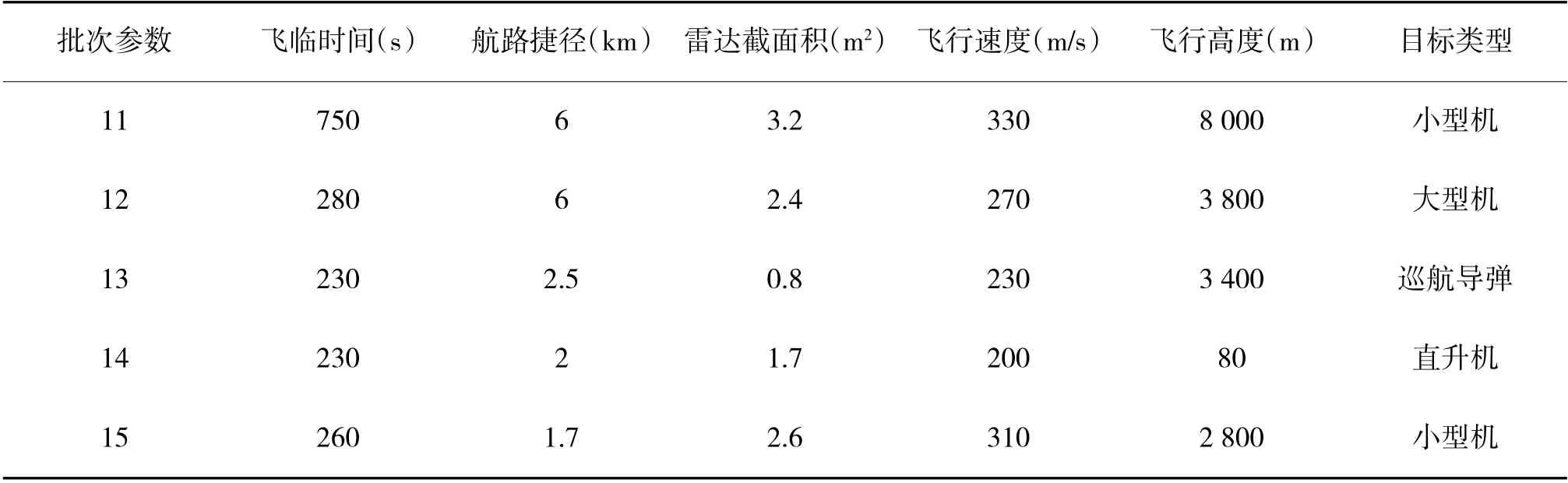
表1 空中目标信息表

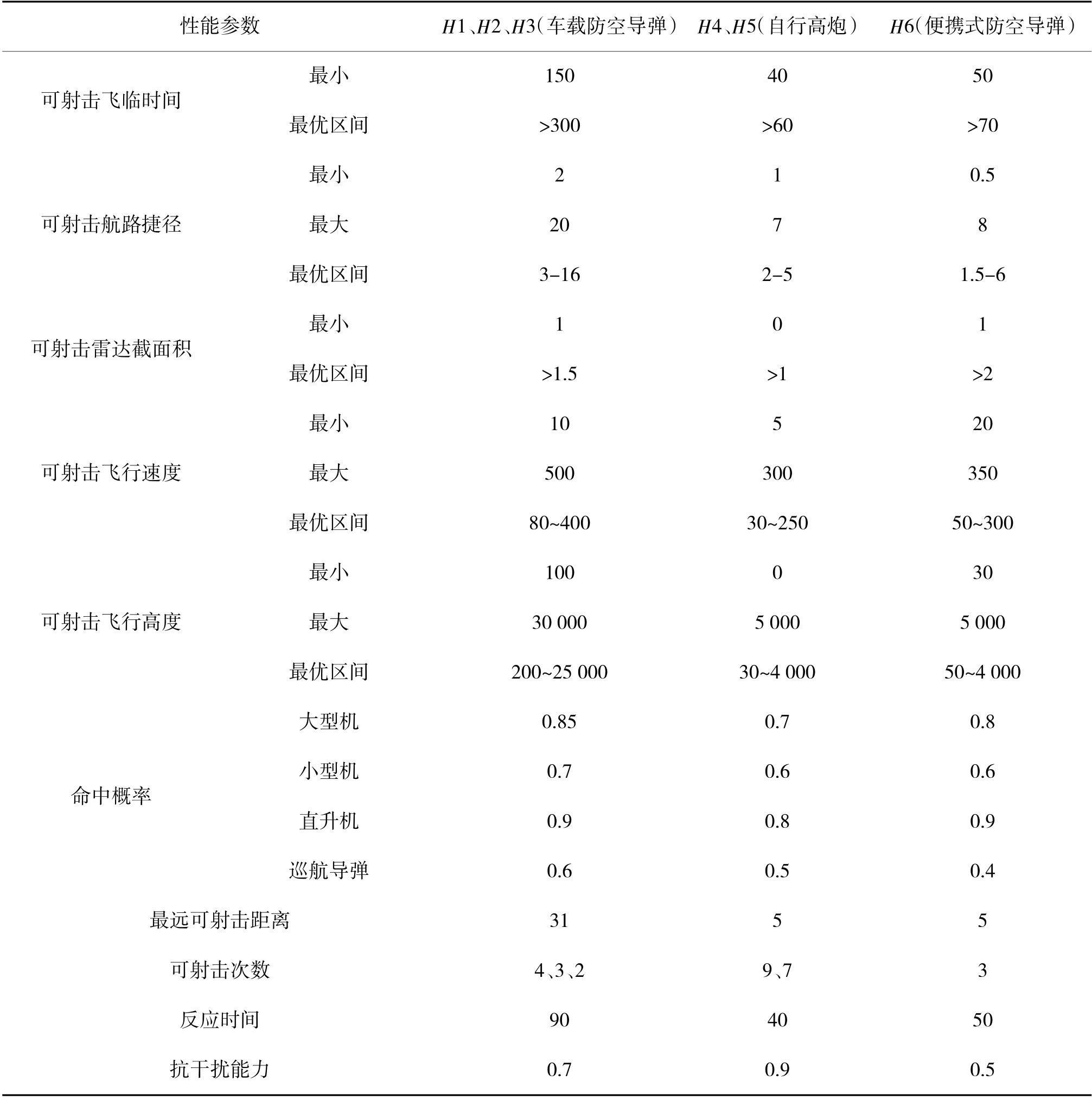
表2 火力单元性能参数

3.1 对空中目标参数赋值

以第11 批目标为例，根据式（1）、式（2）对各空中目标参数进行赋值，可得赋值矩阵：

该矩阵的行依次表示第11 批目标的飞临时间、航路捷径、雷达截面积、飞行速度、飞行高度相对于各火力单元的赋值。矩阵的列表示各火力单元对该目标各参数的有利度赋值，若出现0 元素，则表明该火力单元在此项条件下不满足射击条件，无法进行射击。

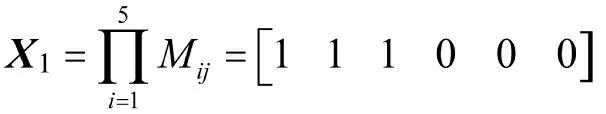
同理可得，X=［0.87 0.87 0.87 0.3 0.3 1］，X=［0 0 0 0.8 0.8 0］，X=［0 0 0 1 1 0.7］，X=［0 0 0 0 0 0.8］。

3.2 火力单元参数赋值

根据式（3）、式（4）对火力单元参数进行赋值（命中概率根据当前的目标类型进行选取），可得赋值矩阵为：

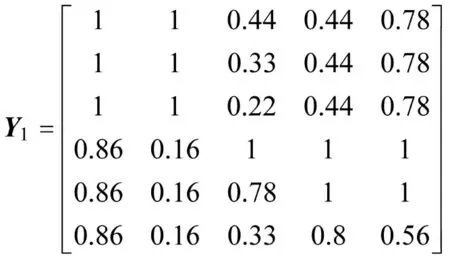
矩阵中的行表示每个火力单元命中概率、可射击次数、反应时间、抗干扰能力4 个参数的赋值情况，列表示同一参数各个火力单元的赋值情况。

3.3 设置遗传算法各参数

1）目标函数，选取Z=sum（X*Y）为目标函数，通过排列Y 的行，从而使得Z 取得最大值。

2）染色体R 的编码方式，采用实数编码，分别代表1～6 号火力单元，各元素的排列次序代表了相应火力单元的射击有利度次序。

3）初始种群规模S 为40。

4）选择方式：采取基于适应度“轮盘赌”的方式进行选取，代沟为0.9，保证每代有4 个优秀的个体向下代传递。

5）交叉方式：采取单点交叉，交叉概率为0.6。6）变异概率为0.05。

3.4 依托遗传算法工具箱进行计算

以第11 批目标为例，经计算可得，在R 取［1 1 1 2 2 3］时，Z 取得最大值10.98。根据式（5）可得1～6号火力单元对第11 批目标的射击有利度依次为（0.71 0.24 0.05 0 0 0）。

同理可得：

第12 批目标，在R 取［4 4 5 5 4 4］时，Z 取得最大值16.50，1～6 号火力单元对该批目标的射击有利度依次为（0 0 0 0.67 0.33 0）。

第13 批目标，在R 取［4 4 4 5 5 5］时，Z 取得最大值6.03，1～6 号火力单元对该批目标的射击有利度依次为（0 0 0 0.71 0.29 0）。

第14 批目标，在R 取［4 6 5 5 4 4］时，Z 取得最大值10.71，1～6 号火力单元对该批目标的射击有利度依次为（0 0 0 0.43 0.33 0.24）。

第15 批目标，在R 取［6 6 6 6 6 6］时，Z 取得最大值2.17，1～6 号火力单元对该批目标的射击有利度依次为（0 0 0 0 0 1）。

3.5 仿真结果分析

通过仿真可以看出，该模型所选取的影响因素数据，均能通过空情信息和己方的配置情况得到，并可直接将原始数据用于计算，不需再加工，提高了模型应用的便利性。仿真结果与实际相符，可为进行火力分配提供依据。

4 结论

本文构建的对空射击有利度分析模型主要有以下特点：

1）对各影响因素赋值，主要是采取同一分配周期内，各参数直接作比的方法进行，该方法可降低各参数对最终结果的影响程度无法精确量化所带来的影响，得出的结果是本分配周期内的相对值，而并非绝对值，更加科学。

2）以遗传算法为计算工具，可以很好地发挥遗传算法自主计算能力强、计算速度快的特点，提高了计算速率和准确性。

3）由于遗传算法本质上是一种随机搜索算法，存在着一定局限，并非每次都能够找到全局最优值，也有可能得到的是局部最优值，个别时候会造成误导。

4）由于本文采取固定空中目标、分析各火力单元的方式进行有利度排序，该方式决定了只能对空中目标逐一进行分析，但是由于计算过程是由计算机完成，速度很快，并不会对指挥员及时处置带来影响。