带残余载波的LSC-DSSS 信号伪随机码盲估计*
潘微宇,赵知劲,,王李军
(1.杭州电子科技大学通信工程学院,杭州 310018;2.中国电子科技集团第三十六研究所通信系统信息控制技术国家级重点实验室,浙江 嘉兴 314001)
0 引言
直接序列扩频(direct sequence spread spectrum,DSSS)具有较强的隐蔽性、保密性和抗干扰性,是最为常见的一种扩展频谱系统。目前,对于短码直扩信号(short code direct sequence spread spectrum,SC-DSSS)和长码直扩信号(long code direct sequence spread spectrum,LC-DSSS)的伪码估计研究已经比较成熟,对结构更复杂的在SC-DSSS 信号上作长码加扰处理的长短码直扩信号(long and short codes direct sequence spread spectrum,LSC-DSSS)伪码估计也已有一些研究成果。在实际通信中,接收端的信号普遍会出现带有一个较小残余频偏的情况,称其对应的载波为残余载波,其加大了LSC-DSSS信号中伪码估计难度。目前,还未见公开发表的对带残余载波的LSC-DSSS 信号伪码估计的研究报道。
未带残余载波的LSC-DSSS 信号伪码估计,主要是利用m 序列的3 阶相关函数(triple correlation function,TCF)特性估计伪码。文献[5]利用延迟相乘消除信息码的影响,并根据TCF 峰值点估计LSC-DSSS 信号的长扰码,但无法估计长码。文献[6]进一步证明了TCF 共同峰与m 序列本原多项式的对应关系,并以此为基础,利用TCF 共同峰和矩阵斜消实现了LSC-DSSS 信号长短码的估计,但在估计时存在较多伪峰,影响估计性能。文献[7]在此基础上,结合拟合优度检验,并利用矩阵斜消法估计非周期LSC-DSSS 信号的长短伪码,但矩阵斜消法只适用于长短码均为m 序列的情况。文献[8]将长码和短码视作复合码,利用特征值分解法估计复合码,再利用TCF 与延迟相乘估计周期LSC-DSSS信号的长码和短码。上述文献均使用3 阶相关法来估计伪码,在较低信噪比下的估计性能不佳。文献[9]提出的梅西算法能够在较低信噪比下估计非周期LC-DSSS 信号的伪码。但上述方法均不能直接应用于有残余载波时的情况。文献[10]利用线性调频Z 变换估计信号的未知载频,并结合交替投影算法估计信息码和伪码,但受系统的频率稳定性影响,存在载频估计误差。文献[11]利用数字锁相环(digital phase locked loop,DPLL)对特征值分解法得到的带残余载波的伪随机码进行跟踪、消除,完成了带残余载波的周期LC-DSSS 信号的长伪码估计,但不能直接估计LSC-DSSS 信号的长码和短码。本文针对带残余载波的LSC-DSSS 信号的伪码估计问题,利用特征值分解法、DPLL 和梅西算法,实现长码和短码的估计。
1 带残余载波的复合码盲估计
假设LSC-DSSS 信号的扩频码与长扰码的码片速率已知且相等,以扩频码码片速率对接收到的基带信号进行采样,并将{0,+1}映射为{+1,+1},则载波频率为f的LSC-DSSS 信号可以表示为:

将接收信号根据长码和短码周期进行二次分段,利用特征值分解和酉矩阵去除位置模糊,实现带残余载波的复合码估计,利用DPLL 对带有残余载波的复合码进行相位跟踪消除,得到无频偏的复合码估计。
1.1 特征值分解法


令V=AS,由于矩阵S 结构的特殊性,根据文献[13]中的模糊矩阵求解算法得到模糊酉矩阵Q,从而可以根据式(7)求出去除了位置模糊的矩阵V。但是由于V 中存在A,所以,V 是被残余载波调制后的S 阵的估计,无法直接估计长短码。

1.2 全数字锁相环消除残余载波

利用图1 所示的全数字锁相环消除残余载波。锁相环主要由鉴相器(phase detector,PD)、环路滤波器(loop filter,LF)和压控振荡器(voltage controlled oscillator,VCO)组成,能够估计输入信号的频率和相位。VCO 采用累加器和正余弦表实现。
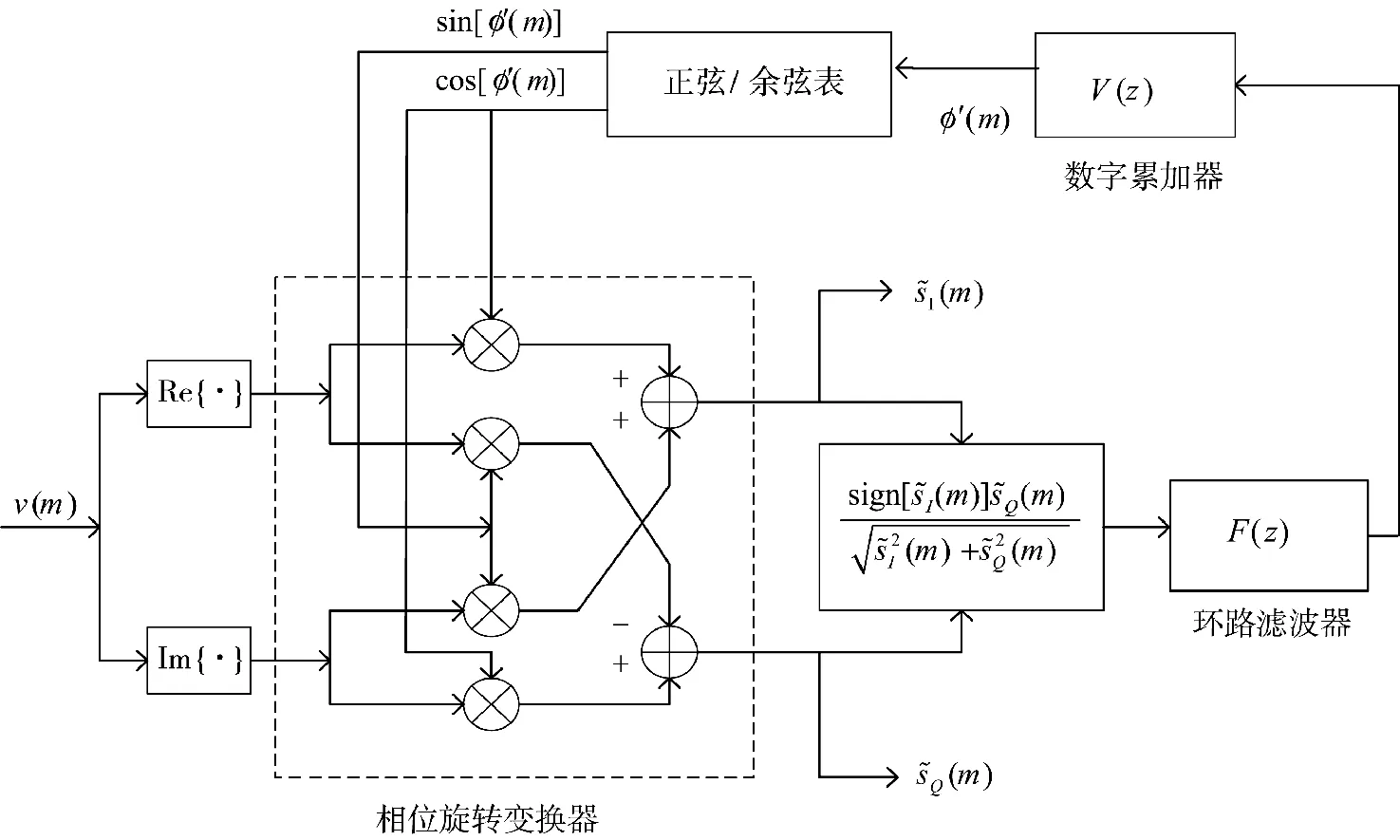
图1 全数字锁相环
将式(8)作为输入信号,该式可等效表示为:
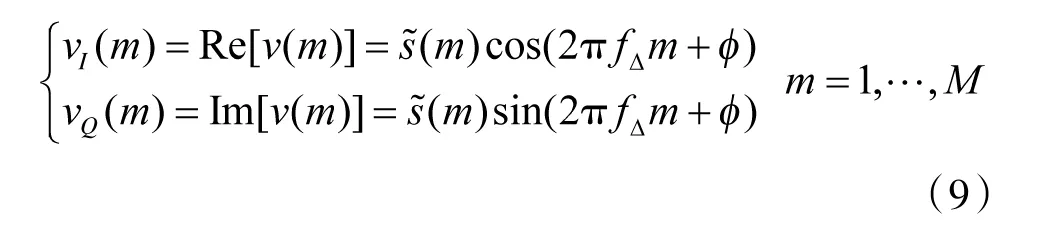
对式(9)作相位旋转,去掉残余载波的调制,得到:


2 长短码估计
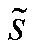
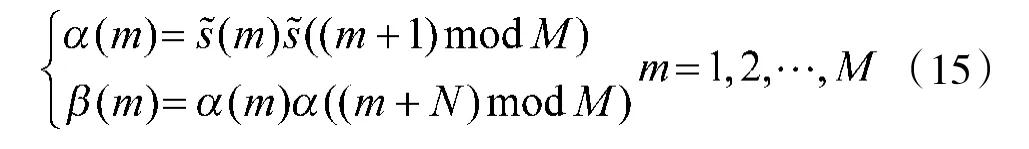
其中,α(m)为消除了幅度模糊的复合码;β(m)为待估计长码。由于长码周期不是短码周期的整数倍,β(m)的(L-1)N 到M 位数据会因为延迟相乘产生较大误差,因此,截取β(m)中前(L-1)N 位数据,利用梅西算法估计长码的本原多项式来恢复长码序列。
2.1 梅西算法


2.2 长短码估计
利用梅西算法求得最短线性移位寄存器后,根据式(18)恢复长码m 序列。

其中,1≤m≤N,α(m)和c(m)分别为估计得到的复合码序列和长码序列。
综上所述,利用梅西算法和相关运算估计长短码的步骤如下:
1)截取序列β(m)的第t 位(设t 的初始值为1)到第(t+2l-1)位的连续2l 位数据,利用梅西算法求序列的生成多项式;
2)根据截取序列中连续的前l 位以及生成多项式,由式(18)生成一个周期长度的新序列,并将该序列向右移动(l-1)位与原序列进行比对,记录对应位置相同的概率,直至搜索完序列β(m)的前(L-1)N 位,选取概率最大的新序列作为估计的长码序列c(m)。
3)根据估计的复合码α(m)和长码c(m),利用式(19)求得短码序列b(m)。
3 算法仿真与实验分析
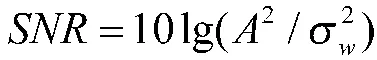
实验1 验证特征值分解法与DPLL 的可行性
长扰码使用8 阶的m 序列,周期M=255,即一个周期的复合码调制L=4 个信息码,固定接收数据段数P=100,残余频偏f=0.02,在信噪比为-8 dB时,消除残余频偏后得到的复合码估计与真实的复合码对比图如下页图2 所示。

图2 估计的复合码与真实复合码对比
由图2 可以看出,最后一段复合码与真实值反向,这与理论相符,通过特征值分解法与DPLL 能够准确估计复合码,使得后续梅西算法与相关运算能够估计出长码和短码。
实验2 接收信号段数对长短码估计性能的影响
长扰码使用10 阶的m 序列,周期M=1 023,即L=16,归一化频偏f=0.02,当接收信号段数P 为50、100 和150 时,本文算法估计的长码和短码误码率曲线如图3 所示。

图3 接收信号段数对长短码估计能的影响
由图3 可知,当P 为50、100 和150 时,使用梅西算法对长码分别在信噪比为-10.0 dB、-9.0 dB、-7.0 dB 下达到准确估计,短码误码率低于1%的信噪比为-9.5 dB、-8.0 dB、-6.0 dB。这是因为P 越大,接收到的信号长度越长,接收信号的自相关矩阵估计就越准确,特征值分解误差就越小,因此,长码和短码误码率越低。
实验3 不同频偏下的长短码估计性能
长扰码同实验2,固定接收数据段数P=150,当残余频偏分别为f=0、f=±0.002、f=±0.02 和f=±0.06时,本文算法估计的长短码误码率曲线如图4 所示。
由图4 可知,有频偏时,本文算法的长短码估计性能有所下降;当|f|相同时,长短码误码率曲线基本相同;随着|f|逐渐增大,估计性能逐渐降低,但性能损失较少。当频偏分别为f=0.002、f=0.02 和f=0.06 时,长短码误码率低于1%的信噪比分别为-9.5 dB、-9.3 dB、-9.1 dB,说明本文使用的全数字锁相环在去除频偏时具有一定的稳定性。
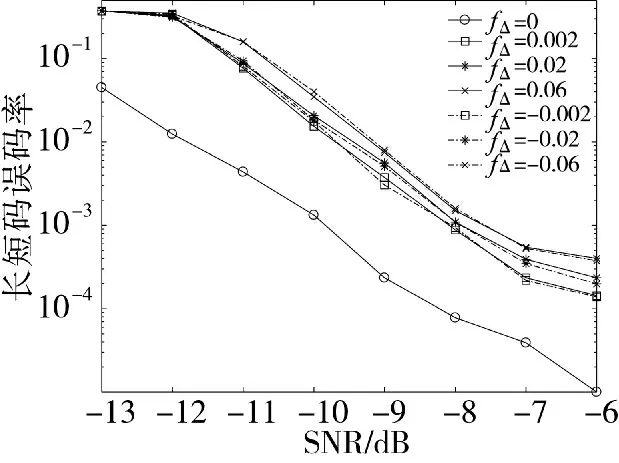
图4 不同频偏下的长短码的估计性能
实验4 m 序列长度对长短码估计性能的影响
接收信号段数P=100,频偏f=0.02,长扰码分别使用阶数为9、10 和11 阶的m 序列,即L 分别为8、16 和32,本文算法和文献[8]算法估计的长短码估计的误码率曲线如图5 所示。
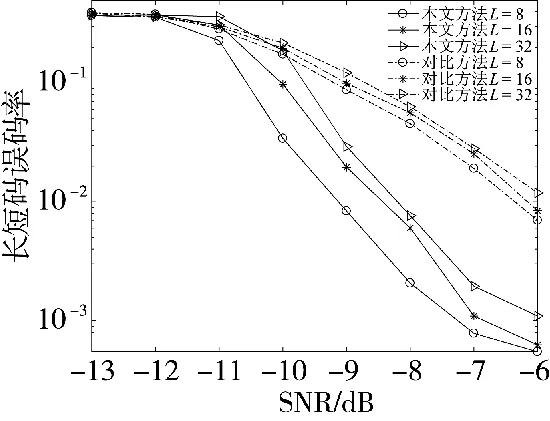
图5 调制符号数L 对长短码估计性能的影响
由图5 可知,1)m 序列越长,长短码估计性能越差。这是因为长码周期越大,则L 越大,所需估计的复合码段数越多,酉矩阵去位置模糊的误差越大,导致复合码的估计性能越差,最终长短码的误码率也就越高。2)与延迟3 阶相关相比,本文算法的估计性能更好。当L=16、误码率为1%时,两种算法所需的信噪比分别为-8.1 dB 和-6.1 dB,本文算法的性能提升了2 dB。
4 结论
本文研究了一种带残余载波的LSC-DSSS 信号的伪码估计方法。将短码和长码作为复合码,利用特征值分解和酉矩阵去除位置模糊实现了带残余载波的复合码估计,并利用DPLL 对残余载波进行跟踪消除,在去除幅度模糊和短码之后,利用梅西算法和相关运算分别估计长码和短码。仿真结果表明,本文算法性能优于3 阶相关法。当频偏为0.02、信噪比为-9.3 dB 以上时,10 阶m 序列和64 位Wlash 码估计的平均误码率可达到1%以下。如何在多径环境下估计长短码直扩信号的伪码是下一步的研究方向。

