三维旋转效应对风力机叶片水滴收集率的影响分析

周文平，汪 异，杨茂立

（1.六盘水师范学院 物理与电气工程学院，贵州 六盘水 553004；2.泸州职业技术学院 智能制造与汽车工程学院，四川 泸州 646000）

0 引言

在冬季低温环境下，高海拔寒冷地区运行的风力机容易发生结冰，从而改变叶片的气动结构，影响材料的载荷、性能等[1]。对叶片结冰进行分析时，相对于操作和维护成本昂贵的结冰风洞实验，数值模拟方便且适用性强，得到了广泛应用。在对叶片表面进行结冰模拟时，首先需要计算叶片表面水滴的收集情况，即水滴收集率[2]。因此，对水滴收集率的分析是准确模拟结冰的前提，也是旋转条件下结冰机理分析的基础。

在进行水滴收集率的计算时，拉格朗日法需要跟踪大量的水滴，不适合复杂的三维旋转物体流场[3]。欧拉法则将水滴视为连续相，并使用体积分数表示给定控制体积内的水量，不需要跟踪大量的水滴，具有明显的优势[4]。在采用欧拉法对大型风力机进行结冰模拟时，由于计算域较大，不少学者采用准三维方法进行结冰模拟。Li Y[5]采用准三维方法对某1.5MW的风力机结冰分布进行计算，研究液态水含量对叶片尖端附近结冰的影响规律。Virk M S[6]基于准三维流场计算和液滴碰撞效率对NREL5MW风力机叶片5个不同位置的冰形进行了分析。相对于三维计算，准三维计算基于动量叶素理论（BEM），计算效率较高，但不能计入旋转叶片边界层内的三维旋转效应。三维旋转效应的存在，不仅会大大改变绕流流场，也会影响水滴收集及冰形预测的精度。不少学者开展了三维旋转效应对空气流场及气动性能的影响研究[7]，[8]，但三维旋转效应对两相流动，尤其是水滴收集的影响研究却鲜有报道。本文采用欧拉法对NREL Phase VI风力机的水滴收集率进行三维和准三维计算，获得不同展向位置水滴在叶片表面的撞击特征，分析了三维旋转效应对水滴收集率的影响，为后续叶片结冰研究打下基础。

1 数值模拟方法

1.1 空气流场计算

本文的研究对象为美国国家可再生能源实验室（NREL）的Phase VI风力机。该风力机由两片叶片组成，翼型采用S809，不考虑机舱及塔架的影响，其主要参数见表1。

表1 Phase VI风力机主要参数Table1Main parameters for Phase VI

计算 域为圆柱区域[图1（a）]。上游 速度 入口边界距叶片中心为5R，下游压力出口边界距叶片中心10R，压力远场边界距叶片中心5R。进行结构网格划分，确保叶片及轮毂表面y+值小于10，网格膨胀率为1.2，以捕捉边界层内流动特性，并对叶片前缘进行网格加密，叶片表面网格如图1（b）所 示。

图1 计算域及叶片表面网格Fig.1 Computational domain and blade surface grids

湍流模型采用对流动分离捕获较好的SST k-ω模型，速度和压力耦合采用SIMPLE算法，离散格式采用二阶迎风。为确认空气流场计算模型的有效性，将低速轴扭矩计算值与NREL实验值进行比较[9]（图2）。由图2可知，即使在较大来流风速时的深失速状态，计算值与实验值仍取得了较好的一致。最大计算误差出现在风速为10m/s时，误差为13.10%。

图2 Phase VI风力机低速轴扭矩比较Fig.2 Comparison of low speed shaft torque for Phase VI

1.2 水滴收集率计算

采用欧拉法计算水滴收集率β时，将水滴视为与空气单向作用、在空间连续分布的液态相。忽略水滴的变形、破裂、聚集及飞溅，且不与空气发生热交换及蒸发，水滴相的质量及动量守恒方程表示为[10]

式 中：ap为 水 滴 体 积 分 数；ρp为 水 滴 密 度，kg/m3；up为水滴相速度矢量；uq为空气相速度矢量；K为两相间动量交换系数。

式 中：dp为 水 滴 直 径，μm；μq为 空 气 粘 度，Pa·s；CD为阻力系数；Re为空气与水滴的相对雷诺数。

式 中：ρq为 空 气 密 度，kg/m3。

β定义为局部区域实际收集到的水滴量与该区域可能收集的水滴量最大值之比[2]。

式中：ap∞为远场水滴体积分数；n为表面法向矢量；upn为水滴与叶片表面相对速度；up∞为水滴远场速度。

为确认欧拉法计算水滴收集率的有效性，对NACA0012翼型在攻角 α=4°，来流速度up∞=105.4m/s，水滴直径dp=20μm，液态含水量lwc=1.3g/m3时的水滴收集率进行计算，并与文献[11]进行比较（图3）。由图3可以看出，不论是收集率最大值，还是变化趋势，计算值和参考值均取得了较好的一致。

图3 NACA0012水滴收集率比较Fig.3 Comparison of collection efficiency for NACA0012

1.3 准三维计算方法

准三维计算方法的基本思路是在叶片上距旋转中心为r的截面上取长度为dr的翼型段，由BEM理论得到入流风速W及攻角 α（图4）。以W及α作为边界条件，对翼型段进行网格划分及流场计算，得到翼型段的气动载荷、水滴收集率等。

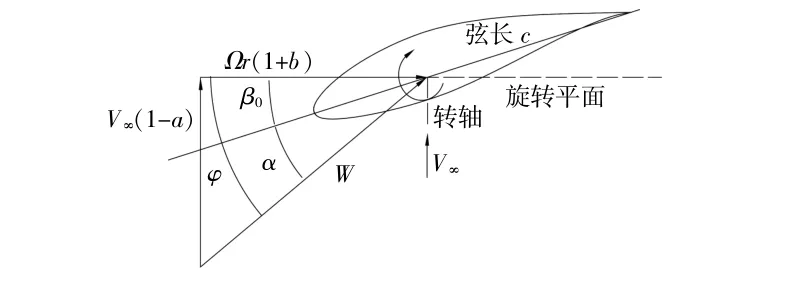
图4 截面速度分布Fig.4 Local velocities at blade section

翼型段的W及α分别为

式中：a为轴向诱导因子；b为切向诱导因子；r为翼型段距旋转中心的距离；φ为入流角；β0为桨距角。

入流风速W及攻角α的计算流程如下。

①假设轴向、切向诱导因子a=b=0。

②由 式（8）计 算α。

③根据α及翼型二维升阻力曲线，得到升、阻 力 系 数Cl，2D及Cd，2D。

④为计入三维流动的影响，采用H.Snel经验模 型[12]对Cl，2D及Cd，2D进 行 修 正 。

式 中：c为 弦 长；Cl，inv为 无 黏 性 升 力 系 数。

式中：α0为零升力攻角。

⑤由BEM理论计算新的轴向、切向诱导因子。

式中：Nb为叶片数；F为叶尖/叶根损失系数。

⑥比较新的诱导因子与上一步的误差，若未达到设置精度，返回步骤②继续进行计算；若达到精 度，根 据 式（7），（8），由 计 算 的 诱 导 因 子 计 算 翼型段的W及α。图5为Phase VI风力机在来流风速uq∞=7 m/s时，BEM理论计算的单位长度叶片上弦长方向的力与CFD计算值的对比曲线。由图5可以看出，即使在叶根及叶尖附近，两者的计算值也比较接近，最大误差为7.86%。

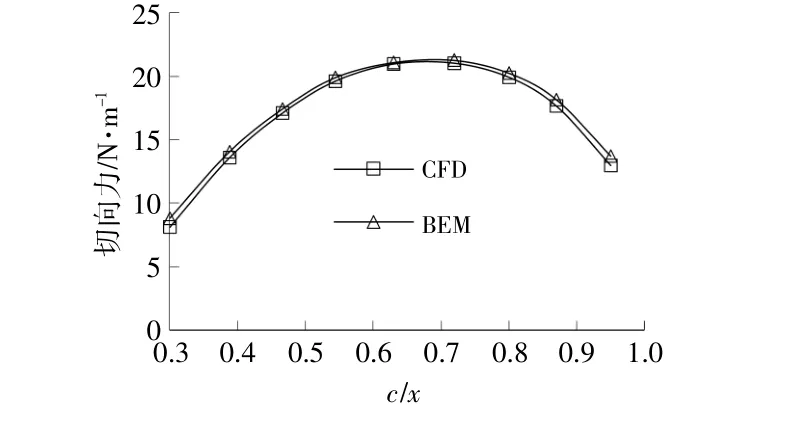
图5 BEM与CFD计算的单位叶展上切向力Fig.5 Tangential force per unit length predicted from BEM and CFD

计算得30%R，63%R及87%R3个截面处的W及α如表2所示。

表2 Phase VI风力机不同展向的W及αTable2Inflow wind speed and angle of attack at different sections

2 水滴相计算结果

对Phase VI风 力 机 在 来 流 风 速uq∞=7m/s，水滴 进 口 速 度up∞=7m/s，水 滴 直 径dp=20μm，液 态含水量lwc=1g/m3时的流场和水滴收集率 β进行三维和准三维计算，分析旋转效应对水滴收集率的影响。

2.1 水滴收集率计算结果

图6为3个展向位置处水滴收集率的计算结果。需要说明的是，根据式（6），采用准三维计算水滴收集率时，应采用翼型W作为水滴远场速度，但为了与三维计算结果进行比较，将水滴远场速度取为三维计算时的水滴进口速度7m/s。

在图6（a）中：准三维计算的最大水滴收集率βmax=0.5348，水 滴 撞 击 区 域（即 β＞0）的x/c为-0.2199～0.0149；三维计算的最大收集率为 βmax=0.6480，比准三维计算结果增大了21.17%，水滴撞击区域的x/c为-0.2328～0.0311。

图6 不同展向截面位置水滴收集率Fig.6 Droplet collection efficiency at different spanwise sections

在 图6（b）中：准 三 维 计 算 的 βmax=2.0230，水滴撞击区域的x/c为-0.1931～0.0253；三维计算的 βmax=2.3153，比 准三 维 计 算 结 果 增 大 了14.45%，水滴撞击区域的x/c为-0.2001～0.0481。

在 图6（c）中：准 三 维 计 算 的 βmax=2.5343，水滴撞击区域的x/c为-0.1455～0.0463；三维计算的βmax=2.7899，比准三维计算结果增大了10.09%，水滴撞击区域的x/c为-0.1533～0.0574。

由图6可知：从叶根到叶尖，最大收集率逐渐增大，压力面水滴撞击区域逐渐减小，吸力面水滴撞击区域逐渐增大；在同一展向位置，三维计算时的最大水滴收集率大于准三维计算，且越靠近叶根附近越明显；三维旋转效应会增加吸力面上的水滴撞击区域，且越靠近叶根增加越明显，但对压力面水滴撞击区域的影响不明显。

2.2 水滴相流场结构

图7为3个展向位置处的水滴相流线图。图中左侧为三维计算结果，右侧为准三维计算结果。

图7 不同展向截面位置流线Fig.7 Streamlines at different spanwise sections

由图7可知：在30%R截面位置，准三维计算时，水滴相在吸力面尾缘附近形成一个分离涡，三维计算时，该分离涡消失，且边界层内流线延伸到吸力面附近后终止；由2.1节计算可知，吸力面尾缘附近的水滴收集率为0，流线终止并不是由于水滴被叶片收集，而是由于离心力的作用，旋转的叶片周围存在沿叶尖方向的展向流动，产生的抽吸作用将吸力面附近的水滴沿展向抽走，使二维截面上的流线终止，并抑制分离涡的形成；在87%R截面位置，由于α较小，准三维流场未发生流动分离，三维流场中也未观察到延伸到吸力面上的流线。上述现象表明，三维旋转效应引起的展向流动在分离流动中影响较大。

2.3 水滴相体积分数

图8为3个展向位置处的水滴相体积分数云图。图中左侧为三维计算结果，右侧为准三维计算结果。

由图8可知，在压力面靠近后缘区域及整个吸力面上，三维计算得到的低体积分数区域的厚度较准三维小，尾流区内水滴缺失的区域也较小，且越靠近叶根差异越明显。这是由于旋转的叶片引起的展向流动，会在弦长方向上产生弦向科氏力，将边界层外的气流及水滴吸入，增加边界层内水滴的体积分数。越靠近叶根附近，翼型α越大，展向流动越明显，因此科氏力越大，边界层内水滴的体积分数越大；越靠近叶尖附近，展向流动越小，科氏力越小，对边界层的作用不明显。

图8 不同展向截面位置水滴体积分数Fig.8 Droplet volume fraction at different spanwise sections

3 结论

本文采用欧拉法对NREL Phase VI风力机在结冰条件下的水滴收集率进行了三维和准三维计算，并分析了三维旋转效应对水滴收集率的影响规律，得到如下结论。

①在同一叶片上，水滴撞击主要发生在叶片前缘附近，沿叶片展向方向，水滴最大收集率及吸力面上水滴撞击区域逐渐增大，压力面水滴撞击区域逐渐减小。

②在同一展向位置，三维旋转效应会使最大水滴收集率增加，还会显著增加吸力面上的水滴撞击区域，但对压力面水滴撞击区域的影响不明显。

③三维旋转效应中的展向流动会将边界层内的水滴沿展向抽出，抑制水滴相流动分离及涡的形成，弦向流动会将主流区的水滴吸入边界层内，增大边界层内水滴的体积分数。

④三维旋转效应对水滴收集率及水滴相流动的影响在叶根附近较大，沿叶片展向方向影响逐渐减弱。