手性药物分子绝对构型鉴定的理论研究进展
朱华结
(河北科技大学化学与制药工程学院,河北石家庄 050018)
目前,很多相关书籍和文献对手性分子的立体化学都有介绍[1-3]。在立体化学研究中,传统的实验方法,如Mosher酯衍生物X-晶体衍射实验等是手性分子绝对构型研究的重要手段。随着理论技术的发展以及计算机计算速度的提高,各种计算方法得到了广泛应用。例如:利用分子对不同偏振光具有不同偏转角度的性质,可以计算其手性分子的特征旋光(specific optical rotation,简称比旋,又简称旋光,即OR,或者[α]);用不同波长下测得的旋光值对波长作图,可得到旋光色散(optical rotatory dispersion,ORD)。此外,还有特征矩阵(matrix)法,利用手性分子对不同偏振光不同的吸收强度,得到电子圆二色谱(electronic circular dichroism,ECD)或者振动圆二色谱(vibrational circular dichroism,VCD)。通过计算这些理论值,并将其与实验值进行比较,就可以确定该手性分子的绝对构型。此外,还有拉曼光学活性(Roman optical activity,ROA)等。随着新计算内容的不断发展,有必要进一步总结相关计算方法。本文主要介绍OR(ORD)、matrix、构象对概念、ECD 和VCD。
1 手性分子的旋光、旋光色散计算及其应用
1.1 手性分子的基本性质
人们对手性分子旋光现象进行详细研究后发现:1)对映体分子的旋光值总是大小相等,旋光方向相反;2)有些分子虽然具有手性,但其旋光值非常小;3)在长链手性分子中,当分子侧链的长度增加到一定程度后,分子的旋光值基本上不随着碳原子数量的增多而有较大变化等。造成这些有趣现象的原因困扰了研究人员很长时间,直到后来因为计算化学的发展而得到了很好的解释。
在缺少高性能计算机的年代,通过量子化学计算方法计算分子的旋光几乎是一件不可能的事情。20世纪50年代,一个有代表性的计算模型是Brewster模型[4],它针对不同的手性分子类型进行了详细而系统的归纳,对促进手性科学的发展做出了巨大贡献。到20世纪80年代,计算机的发展使得量子化学计算成为可能。1982年,AMOS在相关的计算程序中引入了Rosenfeld计算方法[5]。随后发展出了各种计算方法,如Hatree-Fock (HF) 算法[6]、密度泛函理论(density-function theory,DFT)等[7]。后期又有很多其他方法不断被提出[8-11],包括各种软件,如较为著名的Gaussian软件[12]。
在量子化学计算过程中,一个基本要求是需要通过构象搜索软件得到能量最低的和其他能量较低的稳定构象。当一个手性分子具有一个较长的链状结构时,其稳定的各种构象的数量可用公式来估算:3(n-2)(n>3),这里n是单键的数量。例如,正丁烷有3个单键,理论上有3个构象。但是由于1个构象具有较高能量,其分布数量很少,因此,主要是2个稳定低能量构象。当n为一个较大数目的时候,理论构象可达几百乃至几千个,此时利用构象搜索软件可能会出现一些低能量构象不能被发现而导致计算误差偏大等现象。此外,当一个分子有100个以上的构象时,量子化学计算工作会更加艰巨。为了克服量子化学在线性手性分子旋光计算工作中的不足,一个新的基于例子函数的理论模型——矩阵模型应运而生。矩阵模型的出现,不仅解决了线性手性分子立体结构的鉴定问题,也与本文介绍的“构象对”概念及其结论相互支持。
1.2 手性分子旋光计算
1.2.1 手性旋光的量子计算方法
光与电子等微观粒子具有波粒二象性。现代理论对光与电子的各种性质的描述或者计算,都是利用能精确表达的波函数。在量子化学计算研究中,手性分子的旋光可用式(1)计算。对第i个构象而言,其旋光值为
(1)
式中:NA是阿弗加德罗常数;M是分子质量;c是真空中的光速;γ是溶剂校正系数,多数情况下认为是1;β(v) 是分子中与频率有关的电子偶极磁性-偶极极化(electric- dipole-magnetic dipole polarizability)参数;[β(v)]0是气相条件下的β(v)值。
如果一个手性分子有多个构象,那么在完成所有低能量构象的旋光计算后,使用Boltzmann统计,依据各个构象的不同能量和旋光值,就可以得到该手性分子的计算平均值:
(2)
式中:ΔGi是第i个构象的相对能量(Gibbs自由能或者全电子能)。
在使用该公式计算手性分子的旋光时,前面提到的手性分子的那些特性都可以通过计算得到相关的结果。如2个对映体分子的旋光大小相等、旋光符号相反等。但是这个公式不能直观地显示出手性分子的那些特征。
1.2.2 矩阵模型方法(matrix)
为了弥补在线性手性分子旋光计算中量子化学计算的不足,矩阵模型应运而生。该模型利用光的波粒二象性性质中粒子函数的特性,采用数学方法推导而出[13]。同样,对于某个手性分子,在测试的偏振光频率、溶剂、温度等都固定的情况下,矩阵代表了手性分子旋光的本身特性,其旋光值与矩阵等价的行列式的特征值成正比。矩阵表达式可通过数学方法推导得到,结果如式(3)所示:
(3)
式中:mi(i=1~4)为第i个取代基的质量;ri(i=1~4)为第i个取代基的半径;xi(i=1~4)为第i个取代基的电负性;si(i=1~4)为第i个取代基的对称性;a1为取代基中单位原子对旋光的贡献;a2为取代基中单位半径对旋光的贡献;a3为取代基中单位电负性对旋光的贡献;a4为取代基中单位对称性对旋光的贡献;在偏振光频率、溶剂、温度等都固定的情况下,k值是一个常数。
该矩阵的特征值(det(D))的表达式是与矩阵具有同样排列的行列式:
(4)
其分子的旋光值[α]与该矩阵行列式的特征值成正比。从式(3)中得到:
[α]=k×a1×a2×a3×a4×det(D)=k0×det(D),
(5)
式中k0是包含k值在内的一个新的常数。显然,该特征值直观地表达了手性分子的旋光性质。例如:如果某一个对映体分子的矩阵表达式与其等价的行列式的特征值可以表达为
它的另外一个对映体分子,假设是第2个和第3个取代基的位置不同造成的,那么该对映体的特征表达式det(D)′为
通过第3行与第2行的交换,得到一个新的行列式,其特征值为
这直观表示出:这一对对映体的旋光值大小相等,但是方向相反。其他的一些性质,也能从这些公式中得到直观的体现。例如:当2个取代基结构非常相像时,若一个是正丁基,另一个是正戊基,则这2个基团的2行数据会十分接近,从而导致这个分子的旋光值很小。
前面说到,手性分子的链长到一定值时,其旋光值变化较小。例如下列的4个手性醇,其旋光值列在其结构的下面(见图1)。考虑到手性分子在测量过程中的误差,这些OR值已经很接近了。这带来一个科学问题:为什么碳原子数量的增长不能使OR值有较大的变化呢?

图1 手性醇的化学结构及其旋光值Fig.1 Chemical structures and optical rotation values of chiral alcohols
这涉及到另外一个新的理论概念:构象对(conformer pair)[14]。正是因为构象对的存在才使得单纯碳链的增长对OR的贡献变得较小。这里简单介绍构象对的含义,以及为什么可以使用简化模型来代替原来复杂手性分子的理论计算。
首先来看非手性正丁烷的3个构象结构(见图2)。在这3个构象结构中,构象5b能量最高,分布最少,构象5a能量最低,因为构象5c和5d的结构完全对称,因此能量完全相等[14-15]。构象5c的结构不存在对称因素,因此,该构象具有手性,即具有旋光。同样,构象5d也具有旋光。根据对映体的性质,这2个构象的旋光值应该是大小相等,但是方向相反。由于5c和5d的能量相同,因而这2个构象的旋光之和等于零。在这里,构象5c和5d为一对对映体构象。另一方面,构象5a和5b具有对称性,这2个构象的旋光等于零。因此,非手性正丁烷表现出来的净旋光(net OR)值为零。由此例子可以看出:即使分子中没有手性,也并不意味着这个分子的某些构象没有手性,只是所有分子构象的旋光加合为零。

图2 正丁烷的3个构象以及构象5c与5d中的乙基构象分析Fig.2 Three conformations of n-butane and the ethyl conformation analysis in conformations 5c and 5d
同样,在手性2-Cl-丁烷中,也存在与5c和5d类似的构象6c和6d。其中乙基的构象在空间上也是完全对称结构(见图3)。通过量子化学计算(B3LYP/6-31G(d)//B3LYP/6-31G(d)),发现构象6a的能量最低,构象6c与6d的能量分别为0.838和0.506 kcal/mol,二者的旋光值分别为+24.36和-17.90。通过Boltzmann统计,构象6c和6d的净旋光值仅为-1.7。这是一个很小的贡献。对旋光贡献最大的来自最稳定构象6a,其计算值为-48.26。这里,构象6c和6d被称之为构象对。在这个分子中,只存在一对构象对。通过Boltzmann统计计算后,全部构象的OR值为-30,构象对的净旋光值(-1.7)对全部旋光的贡献仅仅占5%左右,对OR的主要贡献还是最稳定构象6a。当分子链的碳原子数增加时,构象对数量将增加很快。但是,无论构象对增加多少,这些构象对的旋光值在经过Boltzmann统计后,所有构象对的净旋光值对旋光的贡献不大[14]。

图3 (R)-6的构象分析与计算得到的各个构象的相对能量以及旋光值、净旋光值
在这个计算过程中,假设构象6c没有被发现,那么计算的OR值将会因为构象6c的正值导致其最后统计的OR值变得较小(-21.6);而如果6d没有被发现,则导致OR值变得负值更大(-35.9)。可见,在构象对中如果存在不完整的构象对,则必然会带来计算误差。低能量的构象对残缺的越多,计算得到的OR值误差就越大。
就目前的计算软件而言,对于简单的手性小分子,基本上能找到所有的构象;然而,当分子较为复杂或者侧链有较长的取代基时,则很难找到所有的低能量优势构象,这势必带来计算误差。以上述手性化合物(S)-4为例,用相关的构象软件发现了92个构象,对其进行叠加,得到如图4[14]所示的叠加结构。

注:白色的圆圈内为核心区图4 使用MMFF94S力场发现的全部92个构象及其叠加图像(固定 C2和 C3 原子叠加)[14]Fig.4 All 92 conformations searched by the MMFF94S force field and their overlay images (C2 and C3 atom fixed)[14]
由图4可知,无论是前视图、侧视图还是俯视图,都存在一定的空域,这表明可能还存在部分没有发现的构象。实际上,软件能找到大部分优势构象,但是因为分子结构的不同,总会有没被发现的构象。不难看出,对分子旋光贡献最大的构象总是碳链结构为锯齿结构的构象。从侧面来看,其乙基结构和长链结构的视图几乎完全一样(见图5[14])。这从侧面说明一个问题:长链取代基对旋光的贡献,因为构象对的存在,其总的构象对对旋光的贡献被相互抵消,只有最低能量的构象才是旋光的最大贡献者。这个从量子力学出发计算得到的结论,与矩阵模型中最小接触半径[13]的使用完全不谋而合,也进一步说明从粒子函数出发推导的理论结果与量子力学计算的结果是一致的。
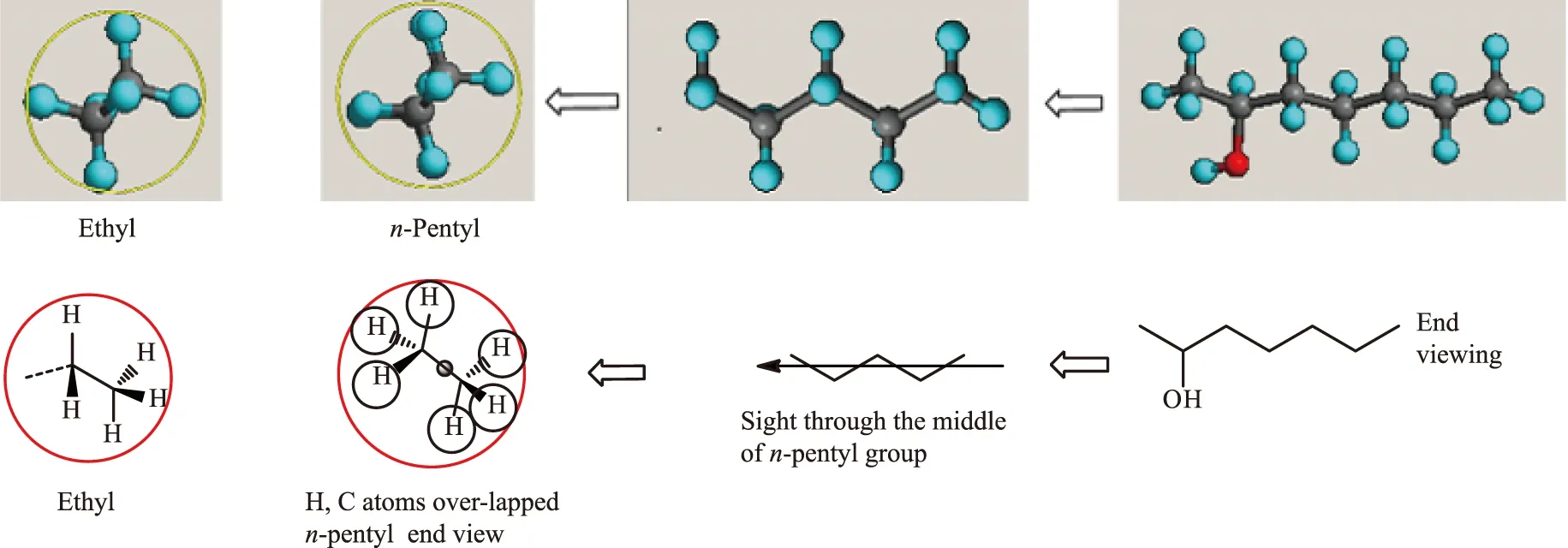
图5 最稳定的乙基和(S)-4结构的侧视图Fig.5 Side view of the most stable ethyl conformation and (S)-4 structures
结合图4中圆圈内密实重叠的构象区域以及图5中的侧视图结构可以看出,长链碳原子对旋光的贡献与短链结构的差别不大。因此,在理论计算中,可将长链碳原子链用短链碳原子链代替,从而减少计算的工作量。这虽然会带来一定的计算误差,但是在另一方面,即使有人使用长链计算,可能会由于部分优势构象找不到,造成构象对的残缺,同样带来计算误差。因此两相比较,在计算误差允许的条件下,使用短链可以极大地减少计算时间和复杂程度,带来的效益会更大。这就是使用简化模型的理论基础。
1.2.3 旋光色散(ORD)
将不同波长下测得的旋光值对波长作图,得到ORD。经常使用的波长有633,589,546,436和365 nm。因此,只要测定得到相关波长下的OR值,并使用测定的OR值与对应的波长作图,即可得到ORD。目前,使用OR和ORD进行绝对构型鉴定的例子还有很多。
1.2.4 使用OR,matrix和ORD鉴定实例
在手性分子结构研究中,通过计算得到分子的旋光值,大多数情况下都能较好地与实验结果吻合。在实际计算中,刚性分子的OR计算结果与实际数据比较接近。例如:对于一个从真菌中分离得到的化合物7(见图6),在使用B3LYP/6-31+G(d,p)//B3LYP/6-31+G(d)方法进行计算后,实验结果与理论计算基本一致,其实验值为+57.4(c,0.005 5,MeOH),在真空条件(又称之为气相条件)下计算的OR值是+74.3。一旦其构象在甲醇中进行优化并计算,得到的OR是+66.2[16],与实验值+57.4更接近。刚性的(5R,11R)-8在B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d)基组下计算得到的OR值为-319,非常接近实验值 (-301)[17]。
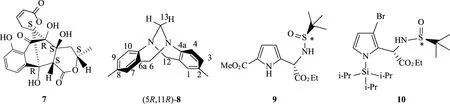
图6 化合物7-10的立体结构Fig.6 Stereochemistry of compounds 7-10
手性药物分子中,绝大部分都是由C,H,O,N元素构成。但是在有些手性药物中也含有其他元素,如含F元素的手性分子。实际上,元素周期表内的元素,其手性分子的旋光值都能通过计算得到。例如:化合物9与化合物10(见图6)[18],分别有S,Si以及Br原子,其OR值都能通过计算方法进行计算。另外,在亚硫酰胺化合物9与化合物10中,还存在另外一个构型结构,那就是亚砜>S=O的手性结构,这种手性也能很好地得到鉴定。
计算出手性分子的OR并与实验值比较来确定手性分子的绝对构型的例子还很多,同时利用手性分子的OR计算,部分手性分子的绝对构型也得到了纠正。例如:化合物11是天然产物(见图7)[19],但是其报道的立体构型是通过与已知结构化合物12的OR值进行对比来确定的[20-21]。

图7 天然手性化合物Bezopyrenomycin和Rubiginone A2及其在氯仿中的OR值Fig.7 Natural chiral compounds Bezopyrenomycin and Rubiginone A2 and their OR values in chloroform
利用OR的符号来比较2个结构类似化合物的绝对构型,很多时候都是正确的。在这个例子中,由于二者看起来结构基本上比较类似,通过比较二者的OR值(化合物11为+38,化合物12为+50),可认为化合物11的C2和C3位的绝对构型也应该为(2R,3S)。但是,当将计算得到的OR值与实验值进行对比时(见表1[22]),发现当化合物11的绝对构型为(2R,3S)时,其旋光值为-12~-86(其中只有一个为+9.5,该计算的基组较低,为B3LYP/6-311++G(2d,p)//B3LYP/6-31G(d))。因此,(+)-化合物11的绝对构型应该是(2S,3R),而不是(2R,3S)。

表1 8种理论计算方法得到的(2R,3S)-化合物11与(2R,3S)-化合物12的OR值[22]
在矩阵计算中,对于系列化合物而言,由于基团相近,结构相似,因此,其k0值接近于一个常数。例如:下列几个系列的化合物,它们的k0值几乎都是常数(见表2[13])。在这些二级碳手性中心分子研究中,计算的构型在k0为(+)时,所使用的计算构型与实际构型一致,这对于鉴定手性中心在长链上分子的绝对构型有较大优势。该方法已经被成功应用到不同手性线性分子的绝对构型研究中[23-24]。而对于三级碳手性分子,k0值为(+)时,计算的产物构型与实际相反,如长链手性分子17(见图8),当计算构型为R时,计算的k0为+0.45,因此其构型为S。

表2 若干个手性醇的特征值(det(D))及其旋光和系数k0值

图8 化合物17的结构以及其det(D)值 Fig.8 Structure of compound 17 and its det(D) value
通过计算OR确定手性构型的例子还很多,读者可以通过这里的介绍,查找到更多的例子。
相对于单一波长下的OR值,ORD能提供更多的信息。由于不同的结构对不同的波长敏感程度不一样,因此不同波长下的OR值更能反映不同分子的结构特性。例如,化合物18(Jonquailine)中C8绝对构型被确定为(R)[25]就是基于其ORD曲线。该ORD是在B3LYP/aug-cc-pVDZ//B3LYP/TZVP气相条件下计算得到的。计算得到的(8S)-18与实验值有很大的区别,而(8R)-18与实验值则很接近(见图9)。化合物18的OR在甲醇中比在氯仿中的大,显示出溶剂对OR值的影响。
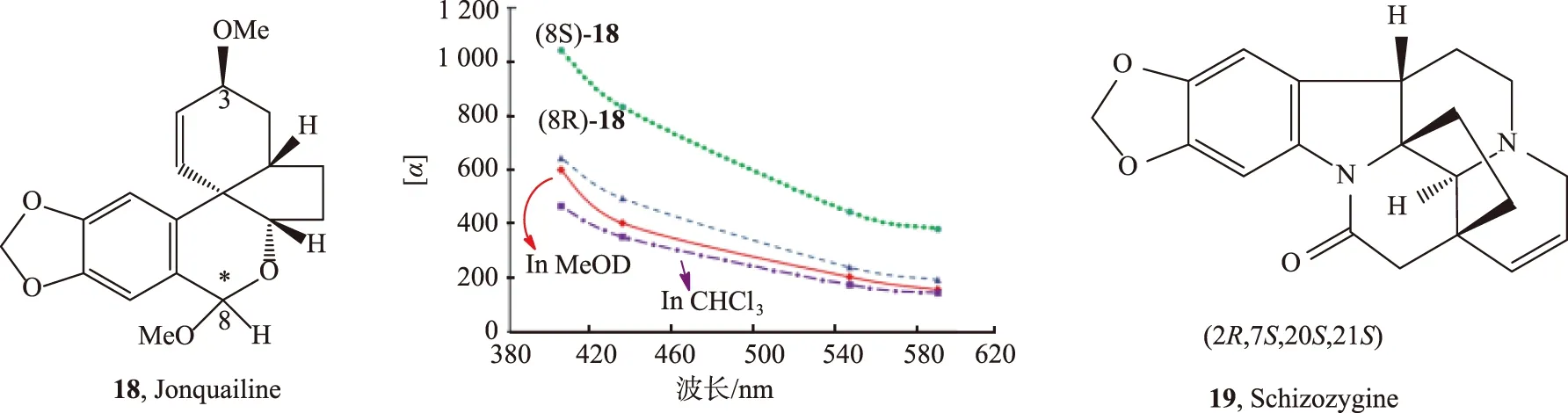
注:实红线—甲醇;虚紫色线—氯仿;绿色点状线—(8S)-18;虚的蓝色线—(8R)-18图9 化合物18的实验ORD谱和计算的光谱 (在气相条件下)Fig.9 Experimental ORD spectra and calculated spectra of compound 18 (in the gas phase)
其他很多分子[26-27],如Schizozygine (化合物19,见图9) 可在B3LYP/aug-cc-pVDZ//B3PW91/TZ2P 条件下计算得到ORD,从而确定其绝对构型为(2R,7S,20S,21S)[28]。其ORD图略。
2 电子圆二色谱及其应用
电子圆二色谱(ECD)又简称圆二色谱(CD),其定义是左旋偏振紫外光(UV)与右圆偏振UV在通过手性物质时吸收强度上的差异(Δε)。即
Δε=εL-εR。
(6)
理论上是不能直接计算得到这种差异的,表征这种差异的是该构象的速度旋转强度R:
(7)
R的单位是 10-40erg-esu-cm/Gauss。该构象分子中的生色团(chromophore)具有多个激发态能量,这样,在某个激发态的圆二色就具有了(+)或者(-)的信号。使用数学表达式(Harada-Nakanishi 方程)将该信号展开[29]:
(8)
得到如下新的方程:
(9)
这里是第j个构象的吸收差异(CD),σ是标准偏差,其定义是该峰高度的1/e时的宽度,不完全等于半峰宽。但是很多报道也称为半峰宽,其实并不准确。这是第i个激发态的波长(单位eV),υ是在υi附近变化的波长,用于ECD的模拟计算。该波长已通过频率转化为eV单位用于计算。
需要使用ECD来鉴定的手性分子,必须具有以下几个基本要求。
1)分子中必须有生色团,如C=C,C=O,苯环等。如果全部都是饱和单键,那么很难使用ECD鉴定其分子的绝对构型。目前,如果ECD设备足够好,能够在UV短波长范围内(如170~210 nm)准确测定其ECD信号,那么对于部分没有生色团的手性分子也能进行鉴定。但是,目前绝大部分ECD设备的有效ECD信号范围都在200~800 nm范围内。对于有机小分子,常用的ECD信号范围仅局限于200~400 nm,因此,手性分子中必须要具备合适的生色团才能用ECD方法。
2)手性分子的手性中心要尽量靠近生色团,如不在生色团附近,则最好不超过3个原子的距离。因为离生色团越远,该生色团受到手性中心的影响越小,在多个手性中心存在时,该信号很可能被其他强的信号淹没,从而出现这种情况:无论该手性中心是R还是S,其计算的ECD信号变化很小,从而在与实验得到的ECD信号相比较的时候,无法确定其绝对构型。一个特殊的情况是:如果有一个具有生色团的手性分子,其所有的手性中心的相对位置都已经确定,只是通过ECD确定其绝对构型,那么可以通过测定与计算ECD就可以鉴定其绝对构型。
通过ECD来鉴定手性分子绝对构型目前是绝对构型研究中的重要手段,成功鉴定的例子非常多,其中有许多经典的例子。生物碱Psychotripine (化合物20,见图10)[30]的相对构型可以使用ROESY等NMR方法确定,计算构型为(3aR,8aR,3a′R,8a′R,3a″S,8a″R)的ECD,可以发现实验结果与理论分析吻合很好 (见图10,σ=0.2 eV),计算方法为B3LYP/6-311++G(2d,p)//B3LYP/6-31+G(d))。其他很多手性分子在使用ECD方法后,都得到了很好鉴定[31-33],如decandrinin(化合物21,见图10)[34]。
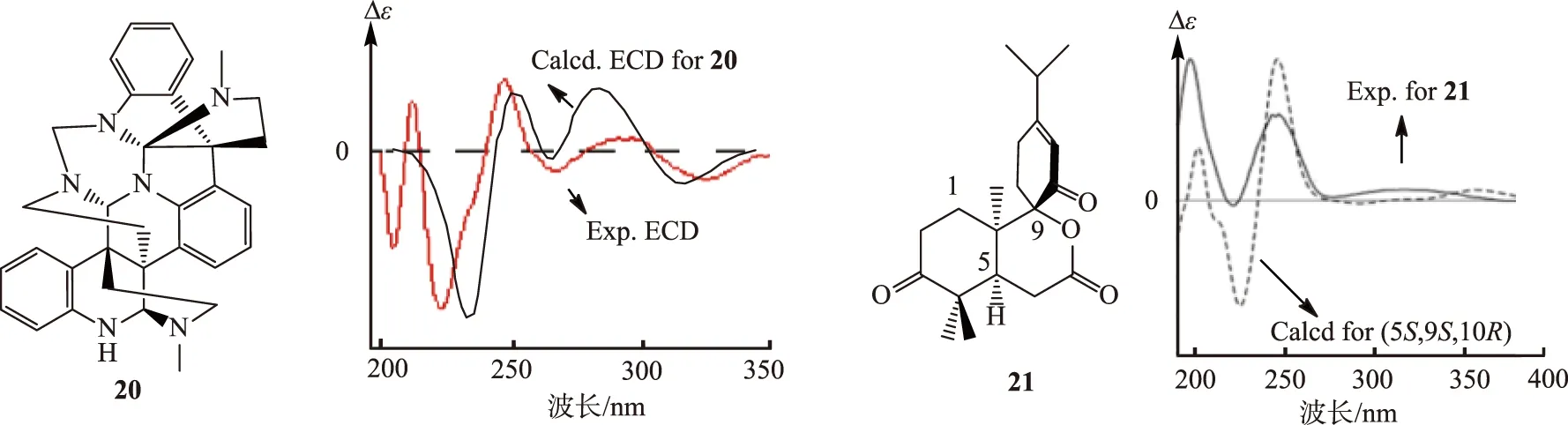
图10 手性化合物20、化合物21的结构及其计算得到的ECD光谱Fig.10 Structure of chiral compounds 20 and 21 and their calculated ECD spectra
3)当生色团在环上而手性中心在链状结构中时,如果手性中心紧邻该生色团,则也可以通过ECD的方法来确定分子的绝对构型。例如化合物22,侧链的C8上有一个手性中心(见图11)[35]。通过计算,鉴定C2的绝对构型为(S)。此外还有其他类似的例子[36]。

图11 计算得到的化合物22的ECD光谱和实验结果的比较Fig.11 Comparison of calculated ECD spectra of compound 22 with the experimental ECD
上述例子中的手性中心在C8上,由于单键的旋转以及C8远离C=C生色团,这些不利因素使得其绝对构型的鉴定较为困难。但是,由于C8上的—OH可形成分子内H键,从而导致其构象相对稳定,因此可以使用ECD的方法来鉴定其绝对构型。
目前,中国ECD的应用研究领域很多,很多学者通过这种技术手段鉴定了很多手性化合物,化合物的类型也丰富多彩,有很多相关报道的例子[37-41]。
3 振动圆二色谱及其应用
3.1 振动圆二色谱概念
振动圆二色谱(VCD)理论在20世纪60年代基本发展成熟,几乎与ECD的发展同步。欧美学者如OSBORNE等[42]、BARRON等[43]和LASSEN等[44]在VCD的发展构成中做出了很大贡献。前文提到,无论ECD还是VCD,都是记录左、右圆偏振光通过手性物质后因不同的吸收差异所形成的光谱。测定手性化合物在偏振IR光下的振动模式,可以得到不同手性物质的VCD光谱。
实际上,量子化学计算也不能直接计算左、右圆偏振光在通过手性物质后不同的吸收差异。其所计算的(如在高斯软件中)是每一个振动频率下的旋转强度(rotational strength)和偶极矩(dipole moment)的值。例如,对第i个构象,其IR和VCD光谱的计算公式[45]如下。
对于IR光谱:
(10)
对于VCD光谱:
(11)
式中:Di是第i个频率下的偶极强度,单位是10-40esu2cm2;Ri是旋转强度,单位是10-40esu2cm2;γ是洛伦兹(Lorentzian)半峰宽,单位是cm-1,在计算中的默认值为 4 cm-1。
3.2 振动圆二色谱的应用
由于VCD使用的是偏振IR光,而分子的振动光谱(即IR)取决于分子各种键的伸缩振动、摆动、扭动等,因此VCD光谱能比ECD光谱提供更多的结构信息,这使得VCD光谱的应用范围比ECD要广。但是,由于IR光能量比UV弱,因此,VCD的测试时间要比ECD长很多,而且需要样品量较大,不同厂家的设备要求也不一样,通常在8~10 mg或以上。
同系列手性分子中,只要其构型相同,这些同系列化合物的ECD光谱基本一致,这使得利用ECD光谱来鉴定同系列手性化合物时很方便。但是在VCD光谱中,即便是结构几乎一样,仅仅只是取代基有变化,例如从甲基变为乙基,这2个结构相似产物的VCD光谱都有很大的区别。这一点与ECD完全不同。
尽管关于VCD仪器很早就有报道,但是商业用VCD仪器差不多到20世纪90年代才上市。目前,VCD光谱的应用普及程度没有ECD高。原因可能在于前文提到的一个关键科学问题:同系列手性化合物的VCD光谱有很大差异,不能通过比对同系列的VCD光谱来确定同系列其他化合物的立体结构。也就是说,每一个手性化合物立体结构的鉴定,都需要借助量子化学计算。同时,VCD信号比较丰富,这一方面是好事,但是另外一方面也带来分析VCD光谱的困难。可能是这两方面的因素,导致目前VCD的应用普及程度不如ECD。
首先研究一下五味子素((+)-schizandrin,化合物23)的VCD光谱(见图12)[46]。五味子是中国传统的中药材,活性成分之一就是五味子素。文献报道的立体结构为(7S,8S)。在完成计算后,将计算得到的VCD与实验结果进行比较,发现在1 430 cm-1附近出现的正、负信号连在一起。而在实验VCD光谱中,正信号在1 430 cm-1附近,负信号在1 470 cm-1。进一步研究其振动模式,发现在这个区域附近,C7和C8键的振动方式与该处VCD信号关联较大。这表明C7或C8的构型有不对的地方。当使用(7S,8S)进行计算时,实验结构与理论分析完全一致,表明正确的绝对构型为(7S,8R)。注意:在进行VCD光谱研究的时候,需要把VCD光谱和其同步得到的IR光谱放在一个区间内进行比较。
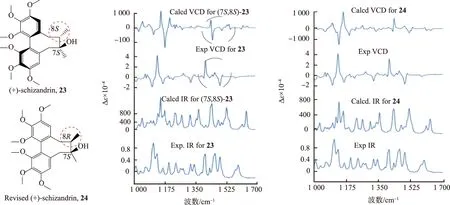
图12 五味子素原始结构(23)、纠正后结构(24)及计算得到的2种立体结构的VCD谱Fig.12 Original structure (23),the corrected structure (24) and the calculated VCD spectra of them
在单手性中心化合物25的绝对构型研究中(见图13),计算的VCD光谱与实验吻合较好[47],由此可以推断化合物25的立体化学为(S)构型(为方便,仅含VCD光谱,其IR光谱省略)。

图13 化合物25的立体结构及其VCD谱Fig.13 Stereostructure of compound 25 and its VCD spectrum
N原子手性是一个有趣的话题。N原子上孤对电子的存在,产生了N原子手性。但是,通常情况下N原子的孤对电子极易翻转,造成N原子的手性不能稳定存在。但是,化合物26(Tröger碱)的N手性稳定(见图14),它能通过HPLC 分离得到(使用CH2Cl2与正己烷为淋洗剂)[48]。VCD光谱的计算在B3LYP/6-311++G(d,p) 基组上完成。计算结果与实验值吻合很好(IR谱省略)。

图14 化合物26实验的VCD和IR光谱以及计算的VCD及IR光谱Fig.14 Experimental VCD and IR spectra and calculated VCD and IR spectra of compound 26
另外一个知名的药物分子是千金藤素(化合物27,见图15)[49-50]。该化合物最早由日本学者发现,目前已成为药物,且对许多疾病都有很好的治疗效果。在目前新型冠状病毒肺炎流行的形势下,中国学者发现了其具有抗新冠的作用。该结果一经报道,立即引起了广泛关注。然而,在立体结构化学层面,这个化合物的立体结构是错误的。也就是说,原来所鉴定的(1R,1′S)的绝对构型不对。正确的绝对构型是(1R,1′R)[51]。该结论已通过VCD 等技术得到了非常好的论证。计算得到(1R,1′R)-27的VCD光谱与实验的(+)-27的VCD光谱一致(见图15)。使用VCD研究手性药物分子的例子很多[52-59],篇幅所限不一一介绍。
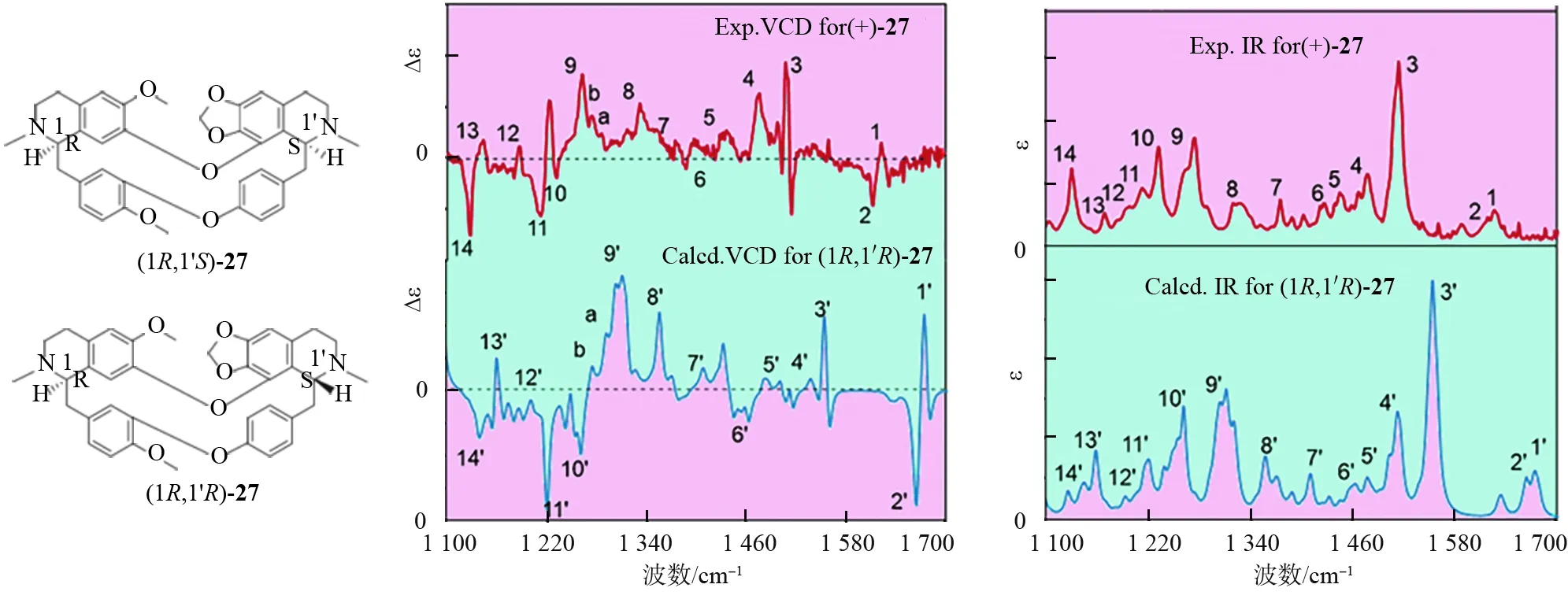
图15 千金藤素原始立体构型(1R,1′S)与正确的立体结构(1R,1′R)及其计算的VCD光谱
实际上,目前计算过程中存在一个较大的问题是很多研究人员对于计算的理解不到位,觉得会用软件就能计算。这是一个很大的误区。能把计算算好需要认真对待计算中的各项科学问题。笔者在最近的一篇综述中,较为详细地探讨了容易出错的一些科学问题[60]。计算化学有它的理论体系和关键的注意事项,每一个理论方法都有其优缺点和使用范围。同时,在完成相关的计算后所面临的数据处理也是一个关键的科学问题。任何细节上的疏忽,都可能带来计算结果的误判。在这个过程中,出错的报导没有国籍限制。部分相关的软件计算技巧等可参阅笔者的另外一本专著《现代有机立体化学》[61],该书在2009年出版时,被列为中国研究生创新学习的参考丛书。
最后一个问题是前面提到的简化模型问题。在实际工作中,研究人员常常使用一个比较简单和小的分子来代替原来比较复杂的分子用于计算。这可以节约计算时间,降低计算成本,同时保证计算结果。因此,使用简化模型带来了很大方便。但是,一个科学问题是:为什么可以利用简化模型来代替原来复杂的手性分子?
如前文在OR计算中使用矩阵模型等系列研究结果中所说的那样,主要是因为构象对的存在。而这一新的概念,也得到相关更广泛的认可[62]。OR的Boltzmann统计计算后,构象对的贡献值很小。例如,在手性化合物17绝对构型的研究中,也可以将长链结构简化为手性结构(化合物28,见图16)。进一步通过计算该化合物的ECD光谱,也证明了其绝对构型是(S)。这个结论虽然是在OR计算的研究中发现的,但在实际上,可以进一步推演到ORD,ECD 和 VCD 的研究中。

图16 手性化合物17的简化模型结构及其ECD计算结果 Fig.16 Simplified model of chiral compound 17 and its ECD calculations
4 结 语
利用计算方法解决实际工作中的科学问题,是理论结合实际科研工作的典型。利用不同的理论方法鉴定手性药物分子的绝对构型具有很大的优势,不仅弥补了实验方法的不足,也进一步促进了新理论方法的应用。利用OR,ORD,Matrix,ECD和VCD方法是目前手性药物分子绝对构型鉴定的有效方法。但是各个方法都有其局限性,使用单一方法用于绝对构型的鉴定已经不是主要方式。目前,使用2种及其以上方法联用成为主要手段。
使用简化模型进行各种计算,如本文中的OR等,这种做法由来已久,但是一直不知道其背后的科学依据是什么,直到以基于量子力学计算的结果为依据,结合构象分析和矩阵模型理论等进行研究,才使这一科学问题(即“构象对”概念)得以完全解决,对此简化模型的应用做到了“知其然也知其所以然”。不同方法以及相关的简化模型应用,将成为今后相当长一段时间内科研人员开展立体结构化学研究的主要手段。

