考虑正压力分配的B-B型涡轮叶片缘板阻尼器系统减振特性研究
何尚文,张 钦,贾文祯,陈 琳,何冰冰
(1.郑州大学力学与安全工程学院,河南郑州 450001;2.中山大学航空航天学院,广东深圳 518107;3.陕西科技大学机电工程学院,陕西西安 710021)
高振动应力引起的涡轮叶片高周疲劳失效一直都是航空发动机振动问题研究的焦点[1]。给涡轮叶片附加干摩擦阻尼器可有效降低叶片振动[2-3],缘板阻尼器因结构简单、适应高温环境、具有良好减振性能等优势被广泛应用于航空发动机涡轮叶片减振[4-6]。常见的缘板阻尼器有2种典型结构:B-G(叶片-基础)型,叶片与阻尼器(基础)耦合,叶片之间动力学不耦合;B-B(叶片-叶片)型,相邻叶片间通过阻尼器产生动力学耦合。通常该类阻尼器在叶盘旋转时产生的离心力作用下与叶片缘板紧密接触,当叶片振动时,缘板与阻尼器之间的相对运动引起的摩擦会耗散振动能量,从而达到叶片减振的目的。
为了提高缘板阻尼器的减振设计能力,国内外研究人员结合阻尼器结构设计进行了广泛研究,主要包含2个方面:B-G型缘板干摩擦阻尼器和B-B型缘板干摩擦阻尼器。对于B-G型缘板阻尼结构[7-10],阻尼器具有无限大切向约束刚度,相邻叶片之间运动学和动力学不耦合;而B-B型缘板阻尼结构相邻叶片之间通过阻尼器干摩擦接触产生运动学和动力学耦合。对于B-B型缘板阻尼结构,文献[11-12]采用集中参数模型对结构动力学特性进行了探究;SCHWINGSHACKL等[13]和PESARESI等[14]采用有限元模型分析了界面参数的不确定性对阻尼器性能的影响规律。PETROV[15]在求解非线性干摩擦系统的稳态响应时采用了高阶谐波平衡法;文献[16]采用时间积分法通过判断接触状态求解了非线性摩擦力与相对位移。相比时域法,在稳态响应为周期且不含次谐波情况下高阶谐波平衡法具有显著的计算效率优势;而在系统稳态响应为非周期或为包含次谐波周期响应时,采用时域法有更好的计算精度;2种方法相互结合、验证可以更好地保证计算精度和效率。以上B-B型缘板阻尼结构研究主要针对阻尼器无切向约束刚度(浮空设计),取得了显著的进展。无切向约束刚度B-B型和B-G型缘板阻尼结构分别对应的切向约束刚度为零和无穷大,是否可以通过切向约束刚度设计提升缘板阻尼器减振性能值得深入研究。
研究表明,在缘板阻尼器的设计中接触面间的正压力是非常关键的参数。李琳等[17]和GASTALDI等[18]结合B-G型缘板阻尼结构,研究了正压力对叶片减振特性的影响规律。阳刚等[19]在建立楔形阻尼器的动力学模型时引入了法向接触刚度,然后由缘板与阻尼器之间的法向相对位移确定接触压力。ZHANG等[20]通过实验对平板阻尼器的接触压力进行了测量,结果表明,振动中叶片缘板与阻尼器间有效接触长度的变化可以引起接触压力的改变。QU等[21]基于平板阻尼器推导了一种新形式的摩擦微分方程,推导中将缘板接触压力假定为离心力的一半。HE等[22]的研究中对一种T型缘板阻尼器进行了动力学建模,建模中将阻尼器离心力提供的接触压力平均分配到相邻两叶片缘板上。在工程中,对于B-B型缘板阻尼结构,叶片缘板与阻尼器间总的正压力需在阻尼器与左、右叶片缘板间进行分配,分配比例随叶片缘板-阻尼器间相对运动变化,可能出现不平均分配,从而影响系统动力学特性。
为提升阻尼器减振设计能力,对比切向无约束的B-B型缘板阻尼结构和切向约束刚度无限大的B-G型结构,本文提出了一种基于阻尼器切向约束刚度设计的B-B型缘板阻尼结构,另根据整圈叶片安装的循环对称性取双叶片结构(如图1所示)进行研究。本研究将基于刚度设计的B-B型缘板阻尼结构简化为三自由度集中参数模型开展机理研究,并在系统动力学建模中重点考虑由叶片缘板与阻尼器之间的相对运动所引起的接触正压力分配,给出基于阻尼器运动的正压力分配计算方法,接触面间摩擦力采用双线性迟滞接触模型进行模拟;基于二分法捕捉粘滑转换点,提升计算精度,给出变步长的四阶龙格库塔方法的系统动力学分析程序,并通过数值仿真研究正压力分配对系统振动响应的影响,以及阻尼器刚度、外激励相位差、总正压力、外激励幅值等关键参数对左、右叶片减振特性的影响规律。

图1 基于刚度设计的B-B型叶片-缘板阻尼器系统结构模型 Fig.1 Structure model of B-B type blade platform damper system based on stiffness design
1 基于刚度设计的B-B型叶片缘板阻尼器系统动力学建模
图1所示为本文研究的叶片-缘板阻尼器系统,阻尼结构由阻尼器和弹性梁组成,弹性梁装配到光滑的叶盘凹槽中,阻尼器假定为刚性且对称地套在光滑的弹性梁上,弹性梁不约束阻尼器沿其长度方向的滑动,发动机旋转时阻尼器依靠离心力沿弹性梁滑动后贴在叶片左、右缘板上且始终保持接触;另外,接触状态下弹性梁顶端不约束阻尼器转动,只提供梁在切向振动的约束刚度。定义正交坐标系oxyz固连在叶盘上,其中x方向为轴向,y方向为切向,z方向为径向。不考虑外激励频率超临界转速的情况,考虑叶片一弯振型(在y方向)下的振动,叶片在x,z方向的振动较y方向振动为小量,可忽略。建立叶片-缘板阻尼器系统的三自由度集中参数模型如图2所示。

图2 基于刚度设计的B-B型叶片缘板阻尼器系统动力学模型Fig.2 Dynamic model of B-B type blade platform damper system based on stiffness design
图2中y1,y2,y3分别为左叶片、阻尼器、右叶片在y方向的振动位移;m1,m2,m3分别为左叶片、阻尼器、右叶片的等效质量;k1,k2,k3分别为左叶片、阻尼器、右叶片y方向的振动刚度;c1,c2,c3分别为左叶片、阻尼器、右叶片相应的线性阻尼系数;Q1,Q3分别为作用在左、右叶片上的气流激振力,存在相位差;N1,N2分别为分配到左、右缘板上的正压力;用双线性迟滞模型模拟左、右缘板与阻尼器之间的接触干摩擦力f1和f3;kd为摩擦接触切向刚度。叶片振动过程中,左、右叶片通过缘板与阻尼器之间的接触力产生相互耦合。依据振动理论和图2所示的叶片-阻尼器系统动力学模型,三自由度动力耦合系统的动力学方程为
(1)
式(1)中接触干摩擦力f1,f3需要结合正压力分配计算和双线性迟滞模型确定,其余参数在后续数值仿真时均参考工程实际和相关研究给定。
1.1 正压力分配计算


图3 正压力分配示意图 Fig.3 Schematic diagram of the normal load allocation
(2)
(3)
叶片振动过程中,阻尼器运动可简化为平面运动,由平面运动的动力学方程可知:
Icxα=N2L2-N1L1,
(4)
式中Icx是阻尼器对过其质心且平行于x方向轴的转动惯量。工作转速下叶片角速度为常量,角加速度α=0,可得:
(5)
综合以上,由式(3)、式(5)可完成正压力分配的计算。显然正压力分配的结果由叶片、阻尼器间相对位移决定,对系统振动特性将产生明显影响。
1.2 接触面间干摩擦力的确定
左、右缘板与阻尼器间正压力确定后,由双线性迟滞摩擦模型确定相应的摩擦力,如图4所示。
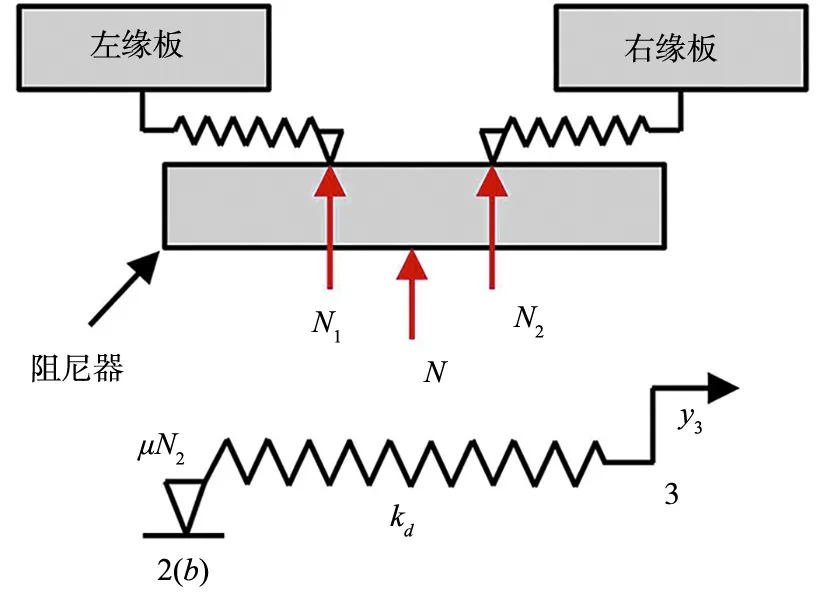
图4 双线性迟滞干摩擦接触模型 Fig.4 Bilinear hysteresis dry friction model
图4中,用2根初始无长度且可屈服的弹簧模拟干摩擦力。以阻尼器与右侧叶片缘板为例,2和3分别为阻尼器和右缘板对应接触点,b为接触面滑动触点,yb描述滑动触点的位移;初始状态下假定滑动触点b与触点2,3重合且相对静止,发生运动后当|y3-yb|小于μN2/kd,b点相对于2点保持静止,否则相对2点运动且使|y3-yb|保持为μN2/kd,同理可建立阻尼器与左缘板间接触摩擦力的模型。设系统运动初始时y1=y2=y3=yb=0,左、右摩擦接触刚度均为kd,则摩擦力可按照式(6)确定:
(6)
可知,当(y1-yb)或(y3-yb)改变正负时摩擦力改变方向,符合摩擦力阻碍运动趋势的原理。
2 基于刚度设计的B-B型缘板阻尼结构动力学特性分析
本文采用数值仿真对基于刚度设计的B-B型缘板阻尼器结构动力学特性进行研究,包含2个方面:一是正压力分配对系统振动响应的影响,二是阻尼器关键设计参数对系统减振特性的影响。
采用四阶龙格库塔时域方法求解动力学方程(1)以获得系统振动响应,并通过二分法捕捉接触面间的粘滑转换点,进一步提高计算精度。根据调谐叶片的性质,可设m1=m3,k1=k3,c1=c3。外激励Q1,Q3均取为简谐力,Q1=F1sin(ω0t+α),Q3=F3sin(ω0t+β),正压力分配按照式(3)、式(5)计算,摩擦力按照式(6)计算。相关参数参考文献[23]给出,具体见表1。

表1 系统的主要参数
2.1 正压力分配对系统振动响应的影响
取外激励幅值F1=F3=300 N,总正压力N=200 N。本文以左叶片为例通过对考虑正压力分配和不考虑分配(平均分配且正压力保持常数)的仿真结果进行对比分析,得到正压力分配对系统振动响应的影响规律。
阻尼器刚度设计值较小时,取k2=5×104N/m,α=β=0(激励无相位差),系统响应等仿真结果如图5所示。

图5 全过程完全粘滞时系统稳态振动响应特性Fig.5 Steady state vibration response characteristics of the system under completely stick condition in the whole process
由图5可知,该参数下考虑正压力分配与不考虑分配的结果保持一致。由图 5 c)可知,系统稳态时摩擦力-相对位移迟滞曲线为一条直线,阻尼器与缘板间的接触在整个稳态周期内都处于完全粘滞状态,附加阻尼器相当于为叶片增加弹性支承,此时阻尼器与2个叶片作为一个整体同步运动,因此2种仿真结果一致。由图5 d)可知,系统响应为周期响应。
阻尼器刚度设计值较大时,取k2=5×106N/m,α=0,β=π(相位差为π表示系统外激励对称),系统的响应等仿真结果如图6所示。

图6 对称荷载下系统稳态振动响应特性Fig.6 Steady state vibration response characteristics of the system under symmetrical load
由图6可知,系统2种仿真结果仍保持一致。主要由于系统是对称的,同时受到对称荷载作用,左、右2个叶片此时发生相向同步振动,等效于正压力平均分配。由图6 c)可知,系统稳态的迟滞曲线是标准的平行四边形(滑动阶段为水平线段),表明2种仿真下缘板与阻尼器间正压力均保持恒定且始终平均分配。由图6 d)可知,系统响应为周期响应。
阻尼器刚度设计值较大时,取k2=5×106N/m,α=β=0,系统的响应等仿真结果如图7所示。

图7 k2=5×106 N/m,α=β=0时系统的振动响应Fig.7 Vibration response of the system at k2=5×106 N/m,α=β=0
由图7可知,2种情况下系统稳态位移时域响应、摩擦力时域曲线、摩擦力-位移迟滞曲线、系统相图均有较为明显的差异。由图7 a)、图7 c)、图7 d)可知,相比不考虑正压力分配,考虑正压力分配时叶片位移出现了一定的整体偏移(静位移)。由图7 b)、c)均可知,相比不考虑正压力分配时正压力平均且为恒定值,考虑正压力分配时整个运动过程中正压力一直变化,特别是完全滑动状态。由图7 d)可知,系统稳态响应仍为周期响应。总之,2种仿真结果下系统动力学特性明显不同,此时系统不处于对称荷载或稳态全过程完全粘滞,考虑正压力分配与不考虑分配(平均分配且振动过程中正压力为常数)的仿真结果出现较大的差异。
综上3种分析可知,系统处于稳态响应对称或全过程完全粘滞(正压力过大也可导致此工况发生)时,系统动力学分析可不考虑正压力分配;除了类似特殊工况,系统动力学分析时考虑正压力分配是必要的。
2.2 基于正压力分配的叶片阻尼系统关键设计参数对系统减振特性的影响

(7)
2.2.1 阻尼器刚度对系统减振特性的影响
取F1=F3=300 N,N=600 N,θ=π/2,定义阻尼器刚度与叶片刚度之比γ=k2/k1,刚度比γ的取值范围为[10-2,102]。图8为叶片减幅率随刚度比γ变化的仿真结果。
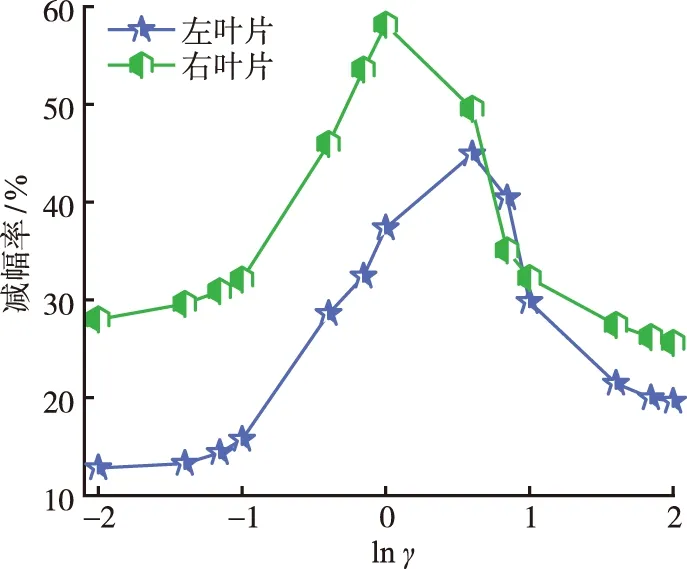
图8 叶片减幅率随刚度比的变化情况 Fig.8 Variation of blade amplitude reduction rate with stiffness ratio
由图8可知,阻尼器的刚度对叶片减振具有显著的影响。左、右叶片的减幅率均随刚度比γ的增加出现先增加后减小的变化趋势,说明存在一个刚度设计范围(阻尼器与叶片的刚度一定程度接近时),使得阻尼器减振效果最佳,这对工程设计具有重要参考价值;相比切向无约束的B-B型阻尼器(刚度比为0)和刚性的B-G型阻尼器(刚度比无限大),通过刚度设计的B-B型阻尼器可以产生更好的减振效果。另外,荷载不对称可以导致左、右叶片的减振效果存在一定差异。
2.2.2 外激励相位差对系统减振特性的影响
取F1=F3=300 N,N=600 N,k2=106N/m(与叶片刚度接近),定义2个叶片外激励相位差θ=α-β,相位差θ的取值范围为[-π,π]。图9为叶片减幅率随相位差θ变化的仿真结果。

图9 叶片减幅率随相位差的变化情况 Fig.9 Variation of blade amplitude reduction rate with phase difference
由图9可知,2个叶片外激励相位差对系统减振效果有显著的影响。左、右叶片所受外激励的初相位一致或相差为π时,2个叶片减振效果一致;相位差在[-π,π]范围变化时,2个叶片减振效果关于相位呈现对称性,这与系统稳态时外激励和摩擦力综合作用关于相位具有对称性有关。在外激励相位相同时,基于阻尼器刚度设计的系统左、右叶片同时具有良好的减振效果。左、右叶片所受的外激励相位差较大时其减幅率表现出明显的差异。
2.2.3 总正压力对系统减振特性的影响
取F1=F3=300 N,θ=π/2,k2=106N/m(与叶片刚度接近),总正压力N的取值范围为[500,800]。图10为叶片减幅率随总正压力N变化的仿真结果。
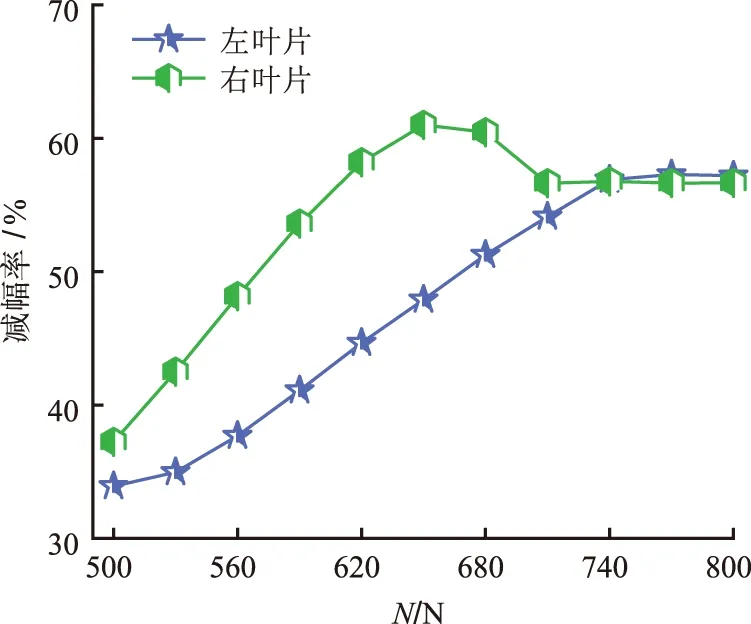
图10 叶片减幅率随正压力的变化情况 Fig.10 Variation of blade amplitude redu-ction rate with normal load
由图10可知,左、右叶片的减幅率均随总正压力的变化而变化。在给定的外激励相位差与阻尼器刚度下,左叶片最佳减幅率出现在稳态响应全过程完全粘滞状态,此时总正压力比较大,系统附加阻尼器相当于附加刚度;右叶片最佳减幅率出现在系统稳态响应存在粘滑转换状态时,此时需要的总正压力比左叶片达到最佳减幅率时要小;在总正压力较大的情况下,存在一个正压力范围使得左、右叶片均具有良好的减振效果。
2.2.4 外激励幅值对系统减振特性的影响
取N=600 N,θ=π/2,k2=106N/m(与叶片刚度接近),假定外激励幅值F1=F3,取值范围为[500,800]。图11为叶片减幅率随外激励幅值F1的变化情况。

图11 叶片减幅率随外激励幅值的变化情况 Fig.11 Variation of blade amplitude reduction rate with external excitation amplitude
由图11可知,外激励幅值对2个叶片的减振效果均有明显的影响。在给定的总正压力、阻尼器刚度和相位差下,左、右叶片的减幅率均随外激励幅值增加出现不同程度的下降,因此外激励幅值增加时需要更大的正压力以保持相当的减振效果。从左、右叶片减幅率的差距随外激励幅值的变化情况可知,在外激励幅值达到400 N时左、右叶片表现出一致的减幅率,外激励幅值小于该值时,右叶片减振效果更好,反之则相反。
3 结 语
本文对比B-G型和切向无约束B-B型缘板阻尼结构,提出了一种基于阻尼器切向刚度设计的B-B型缘板阻尼结构。在动力学建模中重点研究了叶片-阻尼器之间的总正压力随阻尼器与左、右叶片间相对运动在左、右缘板间的分配,给出了基于阻尼器运动的正压力分配方法。编制了基于变步长四阶龙格库塔方法的系统动力学分析程序,通过数值仿真分析了正压力分配对系统振动响应的影响,研究了阻尼器刚度、外激励相位差、总正压力以及外激励幅值对基于刚度设计的叶片阻尼器结构减振特性的影响规律。本文的主要结论如下。
1)除了左、右叶片缘板与阻尼器完全粘滞及系统受对称荷载作用等特殊工况,在B-B型叶片缘板阻尼系统动力学分析中考虑正压力分配是必要的。
2)总正压力、外激励相位差及阻尼器刚度均有一个较大的范围使得系统减振效果良好,这对于缘板阻尼器工程设计具有重要价值。
3)通过阻尼器刚度设计,相比切向无约束B-B型和B-G型阻尼结构,本文提出的B-B型叶片缘板阻尼结构可以达到更好的减振效果。
本文仅基于集中参数模型对正压力分配的方法及一种基于刚度设计的阻尼器系统减振特性开展了初步的机理研究,下一步拟将本文的计算理论推广至有限元模型进行研究,以发展一种基于正压力分配的涡轮叶片干摩擦减振有限元计算方法。

