一种利用卷积神经网络重建的遥感影像Curvelet融合方法

李彦东，隋立春，2，陈楠，袁欢欢，徐家利

(1.长安大学 地质工程与测绘学院，西安 710054；2.地理国情监测国家测绘地理信息局工程技术研究中心，西安 710054)

0 引言

遥感技术因其独特的技术优势，被广泛应用于地球环境监测、土地资源利用变化监测、气候环境监测等诸多领域。遥感影像空-谱融合技术主要是通过融合多光谱影像(multi-spectral，MS)以及全色影像(pan-chromatic，PAN)来构建高光谱高空间分辨率的遥感影像，它已经成为了许多遥感应用预处理过程中的关键步骤[1]。

过去的几十年中，学者们提出了各种各样的方法来解决遥感影像空谱融合问题[2]。最早且经典的是成分替代法，它的主要原理是将多光谱影像首先变换到一个合适的影像空间中，然后合理选取其中某一分量，利用高空间分辨率的全色影像进行替换，最后将影像空间中的分量进行反变换，得到融合后的影像。成分替代方法的关键在于全色影像与替换分量之间的相关性，相关性越大，融合后的光谱差异越小。成分替代法如基于HIS(hue-intensity-saturation)融合[3]、主成分分析(principal comp-onent analysis，PCA)、基于Gram-Schmidt(GS)变换融合[4]等，虽然这些方法可以获得较高的空间分辨率，同时具有较强的鲁棒性，但是由于全色波段与多光谱影像分量只有部分光谱区域重叠，所以它们的相关性本身就有一定的限制，因此这些方法通常存在光谱失真的缺点[5]。

为了降低由于分量替代而引起的光谱失真程度，一些学者提出了基于多尺度分析的融合方法，首先将全色波段影像分解为高频段与低频段，然后将全色波段影像的高频信息注入到低空间分辨率的多光谱影像上，以提高影像的空间分辨率。多分辨率分析方法如小波变换(wavelet transform，WT)、平稳小波变换(stationary wavelet transform，SWT)、Atrous小波变换(Atrous wavelet transform)等[6-7]，基于多分辨率分析的小波变换方法可以保持良好的光谱信息。然而，这些方法可能会遭受严重的空间失真(例如振铃效应)，这样会引起融合影像视觉质量的恶化。近年来，基于压缩传感以及机器学习的影像融合方法得到了关注[8-12]。Li 等[13]提出了一种基于稀疏诱导先验信息的压缩感知方法，通过建立随机抽取高分辨率多光谱影像的影像块字典来增强稀疏性。另一方面，深度学习，特别是卷积神经网络(convolutional neural networks，CNN)已经成为影像识别、影像增强、目标检测和超分辨率等领域的研究热点。Dong等[14]提出了一种超分辨率卷积神经网络(super-resolution convolutional neural networks，SRCNN)，并成功应用于超分辨率处理。在此基础上，Masi等[15]提出了一种全色波段锐化的卷积神经网络(pansharpening neural networks，PNN)。全色锐化可以看作是一个多输入单输出问题，而SRCNN最初是针对单输入单输出情况设计的，PNN与SRCNN的主要区别之一为是否将全色影像的细节信息注入CNN模型中。PNN模型已成功地应用于实际数据，并获得了高质量的影像融合结果。

传统的多光谱影像融合方法主要是将全色影像的空间细节和多光谱影像的光谱信息结合起来，简单地将多光谱影像通过插值的方法(邻域插值、双线性插值等)进行放大，然而由于放大后多光谱影像与全色影像的空间结构有较大差异，导致融合影像产生畸变，因此，降低多光谱与全色影像之间的差异有助于提高融合影像的分辨率。

为此，本文提出了一种顾及多光谱分辨率空间信息的影像融合方法。首先，利用Wald协议构建低分辨率全色影像，利用SRCNN网络来训练低分辨率和高分辨率全色影像之间的关系，将训练好的网络应用于多光谱影像的重建以代替传统插值重建的方法；其次，为了充分利用分量替代法保留原始影像空间信息以及多分辨率分析保留影像光谱信息的优势，在GS变换的基础上，加入Curvelet变换分析，进一步提高多光谱影像与全色波段影像的融合质量。用SRCNN进行空间分辨率增强，可以减小低分辨率影像与全色影像空间结构之间的差异，提高其相关性，有利于降低分量替换引起的光谱失真；同时，Curvelet变换可以较好地保存原始多光谱影像的光谱信息，有利于融合影像视觉质量的提高。

1 算法介绍

1.1 超分辨率卷积神经网络重建

在多光谱遥感影像融合处理过程中，首先需要将多光谱影像通过插值的方法放大到与全色影像相同，插值方法多采用双线性内插或双三次插值，这种简单的放大并不能提高多光谱影像实际的分辨率。实际上，低分辨率影像与其对应的高分辨率影像有着共同的先验信息[16]，这就使得低分辨率影像可以通过自身的细节来提高空间分辨率。SRCNN具有结构简单、学习速度较快等特点，是一种端到端的映射。

本文利用SRCNN模型来增强低分辨率多光谱影像的空间信息。在模型训练阶段，将低-高分辨率的全色影像作为网络的输入-输出；网络通过学习低-高分辨率全色影像之间的关系，获得二者之间的空间细节信息。利用学习到的网络代替传统插值重建方法，对多光谱影像所有波段分别进行SRCNN重建，得到增强后的多光谱影像，从而提高多光谱与全色影像之间的空间相关性，降低后续融合过程中产生的畸变，重建过程如图1所示。

SRCNN模型主要包含特征提取、非线性映射、影像重建三个模块。

1)特征提取。将低分辨率PAN影像进行分块，每个小块视为一个高维向量，这些向量组成一个特征映射，其大小等于这些向量的维度，表示如式(1)所示。

H1=max(0，F1×I+R1)

(1)

式中：F1为滤波器，其大小为f1×f1×n1，n1是滤波器的数量；I为低分辨率影像；R1为偏差，大小为n1×1维；H1为通过卷积操作得到的特征映射，即第一卷积层。

2)非线性映射。将提取出的特征映射到另一个高维向量上，每一个映射向量表示一个高分辨率小块，这些向量组成另一个特征映射，非线性映射层表示如式(2)所示。

H2=max(0，F2×H1+R2)

(2)

式中：F2为卷积滤波器，大小为n1×1×1×n2(n2≤n1)；R2为n2×1维的向量；H2为非线性映射后的输出特征，每个输出的n2维向量表示一个高分辨率块，用于后续的重建。

3)影像重建。将来自非线性映射层的高分辨率块进行聚合，从而生成高分辨率影像，重建层的表示如式(3)所示。

H=F3×H2+R3

(3)

式中：F3为重建层滤波器，大小为n2×f3×f3×c；R3为一个c维向量；H为重建后的高分辨率影像。

1.2 Curvelet变换原理

传统分量替代方法在融合过程中容易产生影像光谱失真，本文采用Curvelet变换分析分离影像高低频信息，在融合影像空间信息的同时保留其光谱信息，以此提升融合影像的质量。Curvelet变换是在小波变换基础上发展起来的，小波分析的优点在于它比傅里叶分析能更“稀疏”地表示一维分段光滑或有界变差函数。然而，小波分析不能“最优”表示含线或者面奇异的高维函数，在二维影像中，小波分析并不能充分表达影像的边缘特征。为了克服这个缺陷，多尺度几何分析受到了关注，其中代表的有Ridgelet变换、Curvelet变换、Contouret变换等。Curvelet变换通过对Radon域的多角度投影变换加强了影像边缘信息的提取，同时，还具有小波变换不具备的方向参数，能够准确地表达影像的边缘方向[17-19]。

Curvelet变换的低频段可以较好地表达影像的整体平滑信息，高频段可以很好地表达影像细节变化的特征。将其用于影像融合中，可以使高分辨率影像的空间细节特征被更好地表达，从而将更多的高频信息注入到低空间分辨率影像中，降低融合后的空间失真。本文采用二代Curvelet变换方法[20]，首先，将融合影像中需要替换的影像从空间域变换到频率域;然后，在频率域中进行局部化;最后，采用二维傅里叶逆变换得到曲波系数。

二代曲波变化与一代曲波变换构造上完全不同，摆脱了一代曲波变化数据冗余的缺点，算法更简单，更便于理解。

1.3 本文算法

图2概括了本文所提算法，即以Gram-Schmid变换为基础，对GS算法的输入及成分替换部分进行改进。SRCNN可以在保留多光谱影像光谱信息的同时提高其空间分辨率，从而提高与全色影像的空间相关性。在GS成分替换时，加入Curvelet变换分析，可以有效地分离影像高低频信息，较好地保持融合影像的空间与光谱信息，本文算法流程如下。

1)空间分辨率增强。根据图1的SRCNN模型，通过对高/低分辨率全色影像进行训练，对多光谱影像进行超分辨率影像重建，得到增强影像Emul。

2)利用增强后的影像Emul进行低分辨率全色波段模拟，作为GS变换的第一分量，模拟原则如式(4)所示。

(4)

式中：GS1为变换的第一分量；N为多光谱影像波段数；Bn为多光谱影像第n个波段。

3)利用模拟的第一分量与增强影像进行GS正变换，变换如式(5)所示。

(5)

式中：GSn为当前第n个变换的波段；Bn为参与变换原始多光谱第n个波段；μn为第n个波段的均值；GSm为已经参与变换的波段；φ(Bn，GSm)为两个波段的协方差。

4)将模拟的第一分量GS1与全色波段进行分量替换，利用Curvelet变换对两幅影像分别进行尺度分析，低频采用绝对值取大，高频采用局部方差准则进行融合(式(6))。

(6)

式中：SL为融合影像低频部分；GS1L为GS变换第一分量低频信息；PL为全色影像低频信息。

局部方差准则将待融合的两幅影像高频信息分成K个子块，对每个子块影像进行方差计算，融合系数的计算如式(7)至式(9)所示。

(7)

(8)

ω2=1-ω1

(9)

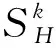
5)将融合后的影像S代替第一分量GS1，然后进行GS逆变换，从而得到融合后的高分辨率多光谱影像。

2 实验结果与分析

为了验证本文所提算法的有效性，实验测试数据使用了不同分辨率的卫星数据集，即Landsat 8、ZY-3以及高分一号进行影像融合重建实验。实验所选取的评价指标为峰值信噪比(peak signal noise ratio，PSNR)、光谱角制图(spectral angle mapping，SAM)、空间相关系数(spatial correlation coefficient，SCC)[21]、通用影像指数(Q)[22]和相对无量纲全局误差(erreur relative globale adimensionnelle de synthèse，ER-GAS)。

2.1 评价指标

1)PSNR。PSNR用于评价融合影像与参考影像的接近程度，PSNR值越大，融合影像失真越少，越接近参考影像。

2)SAM。SAM的结果可看作两影像之间整体余弦角均值。SAM值越小表示两个影像越匹配，相似度越高；反之，表示两影像相似度越小。

3)SCC。SCC表明融合影像与全色影像之间空间细节的相关程度。SCC数值越大，代表融合方法保持空间细节信息的能力越强。

4)Q。Q值越大，影像融合效果越好。

5)ER-GAS。ER-GAS主要从光谱角度评价融合影像的质量，反映了光谱整体的变化情况。ER-GAS数值越小，代表影像融合效果越好。

2.2 训练数据说明

实验数据根据Wald协议进行模拟，首先通过双三次插值按其空间分辨率对多光谱及对应的全色影像进行下采样，然后对下采样后的影像进行融合，同时将原始的多光谱影像用作地面真实的参考影像。

SRCNN网络参数通过本文所给的训练集重新进行训练，特征提取层滤波器F1大小设置为9×9×64，非线性映射层滤波器F2设置为64×5×5×32，重建层滤波器F3设置为32×5×5×1；目标函数采用均方误差；使用带有动量参数的随机梯度下降法(stochastic gradient descent，SGD)最小化目标函数，初始学习率设置为0.01，权重衰减设置为10-7，动量参数设置为0.9。

训练集为三组实验数据,在上采样阶段选取2、3、4三种不同融合尺度分别进行训练，训练数据说明如表1所示。

表1 训练数据说明

2.3 融合结果分析

图3、图4、图5分别为不同融合尺度的遥感影像。从目视融合效果上看，针对不同融合尺度的遥感影像，所有算法均有效地提高了影像细节信息，影像质量都得到了改善，不同地物地貌可以更加容易地被识别出来。针对不同地貌的影像，GS、PCA等成分替代方法都较好地增强了影像的空间细节，但在图3标记的红色区域，存在明显颜色失真。将图4中标记的红色区域进行比较，可以看出小波与曲波变换更接近真实景物效果，影像光谱效果更接近参考影像，但其空间细节表达能力不足。将图5中红色区域对比来看，多尺度分析算法在建筑物边缘细节表现出一些空间混叠，成分替代方法则出现了一些色差，本文算法在视觉上更接近参考影像，一些地面细节及纹理特征更加清晰。面对不同融合尺度的遥感影像，本文所提算法综合表达能力更突出。

表2、表3、表4给出了不同融合尺度下融合算法的客观评价指标。对比分析可以看出，本文所提算法均优于对比算法。从光谱角制图指标上看，本文所提算法比其他算法均提高了0.1以上，表明其在融合过程中有着很好的光谱保持能力，对于后续利用遥感影像光谱特征进行分类分割起到了至关重要的作用。对比空间相关性指标，本文所提算法在Landsat 8影像上融合效果相较于其他算法略有提升，在ZY3-1、GF-1融合结果上有明显提升，这一方面是由于原始多光谱影像经过SRCNN影像重建，其空间细节信息有了明显增强，对于融合影像的空间信息有促进作用；另一方面，增强多光谱影像空间细节有助于提高与全色影像的相关性，降低了融合过程中影像的光谱失真，在图3、图5红色标记区域中有所体现。通过与其他三种指标进行对比，可以发现本文所提算法指数最高，这显示了本文所提算法在光谱保真度及空间增强方面优于传统的成分替代及多尺度分析融合方法。

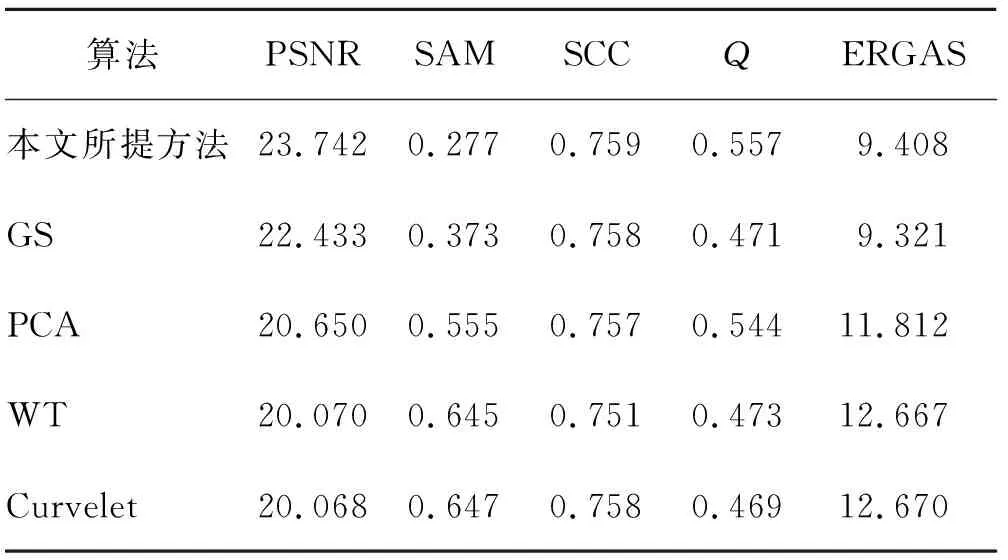
表2 Landsat 8影像不同算法指标对比

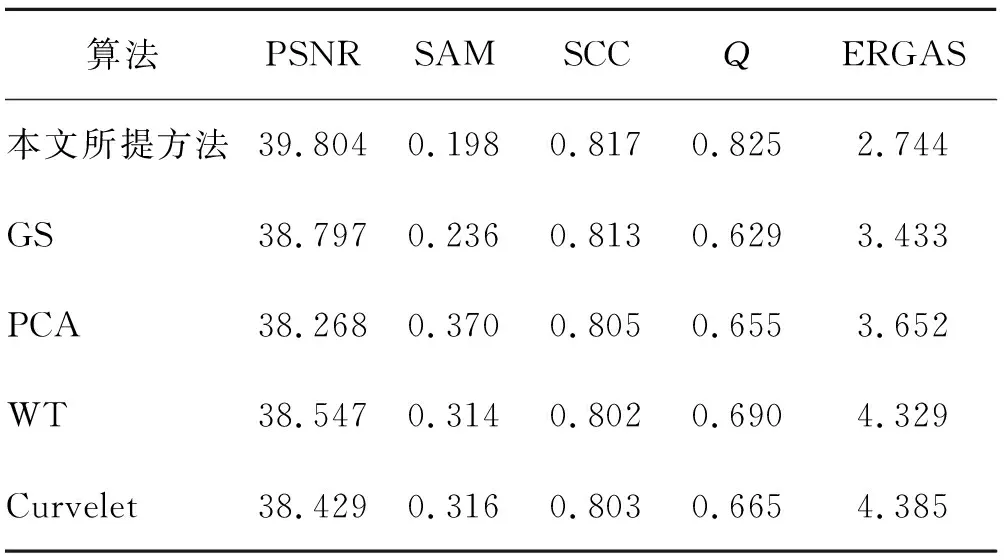
表3 ZY3-1 影像不同算法指标对比

表4 GF-1 影像不同算法指标对比

通过目视判读以及指标对比分析，GS、PCA及目标算法在表达影像空间细节信息方面有着明显优势，多尺度分析算法及目标算法在光谱信息方面更接近参考影像，说明目标算法不论从光谱保持能力还是细节表现程度上都有着出色的融合效果。同时，面对不同的融合尺度，不同卫星影像的波段信息及分辨率都有着较大的差异，本文所提算法也能展现出较好的融合效果，说明了本文所提算法的有效性以及对不同数据的适应性。

3 结束语

本文通过超分辨率影像重建对原始多光谱影像进行空间细节提升，同时在传统GS变换基础上加入Curvelet变换，结合二者优点，提出了基于SRCNN与Curvelet变换的多光谱遥感影像融合方法。实验结果表明，本文算法在整体上优于已有的分量替代及多尺度分析算法，具备GS算法与Curvelet变换的优势，能够在保持影像光谱信息的同时，极大地提高影像的空间分辨率，改善了融合影像的质量。

然而，本文算法在多光谱影像重建阶段选取的是全色影像作为训练样本，如何在现有的基础上探究全色影像与多光谱影像之间的联系，以及有效地利用遥感影像先验知识(如NDVI等信息)进一步提升多光谱影像重建质量，这一方面的内容有待研究。同时，考虑到Curvelet变换中多个方向参量之间代表了影像不同的细节纹理特征，如何在影像训练阶段利用这一特性提高训练效率及精度，值得一定的关注。