基于机器视觉的养殖鱼摄食行为识别方法

李济泽，位威，张凯凯

(福建工程学院 机械与汽车工程学院，福建 福州 350118)

目前，人工投喂仍是最常见的养殖鱼投喂方式，但该方式严重依赖人工经验且人工成本增长较快。近年来，养殖鱼自动投喂技术获得越来越多的关注，但现有的自动投喂方式大多不能根据养殖鱼的实时摄食情况及时调整投喂量，容易导致饵料投放不足或过量[1]，而投喂过量或投喂不足都会对水产养殖带来不利影响，造成经济损失。机器视觉技术因其非入侵性、经济和高效的特点，逐渐成为渔业生产过程中的重要研究手段。钱阳[2]、PARRA L等[3]和BALLESTER-MOLTM等[4]提出通过对目标水域剩余浮饵的计数来量化养殖鱼的摄食活性。Sadoul等[5]提出使用养殖鱼的聚集面积来评估养殖鱼摄食活动，但该方法不适用于高密度的养殖环境。陈彩文[6]基于图像纹理特征提出了一种养殖鱼的摄食行为识别方法，但其识别准确率有待提高。陈志鹏等[7]将光流法和纹理特征相结合来识别养殖鱼的摄食行为，但光流法的计算量大且易受噪声、光照和环境扰动的干扰。此外，针对实际养殖环境中光照不足的情况，周超等[8]提出了一种使用红外相机采集图像，直接提取养殖鱼图像的5维纹理特征，并使用支持向量机对摄食强度进行分类，但分类准确率偏低。本文将养殖鱼摄食图像纹理特征增加至20维，并且使用支持向量机识别养殖鱼摄食行为。

1 养殖鱼摄食行为特征的提取

1.1 养殖鱼摄食图像采集

养殖鱼视觉监测系统主要由近红外相机、红外补光灯、支撑架、计算机等组成，该系统可以连续获取鱼摄食图像，结构如图1所示。

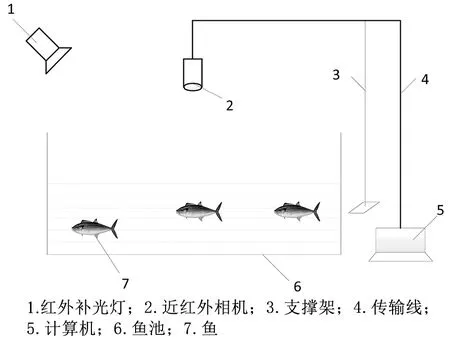
图1 养殖鱼视觉监测系统

1.2 养殖鱼摄食图像特征提取

养殖鱼整个摄食过程中，养殖池水面纹理会有明显的变化，摄食开始时因鱼争抢饵料会激起水花，水面剧烈波动，随着摄食的进行，水花会逐渐减少，水面也逐渐归于平静。并且鱼摄食激起的水花和水面的波动，导致像素点的灰度和梯度变化都较为剧烈，因此可以从图像的灰度和梯度信息中提取纹理特征。

1.2.1 基于灰度共生矩阵的纹理特征

灰度共生矩阵描述了图像中相距一定距离的两个像素之间的灰度关系，设f(x,y)为一幅二维数字图像，其宽、高为M像素和N像素，灰度级为Ng，则其灰度共生矩阵可写为：

P(i,j)=#{(x1,y1),(x2,y2)∈

M×N|f(x1,y1)=i,f(x2,y2)=j}

(1)

式中，#(x)表示集合x中的元素个数；P为矩阵，其大小为Ng×Ng，如果点(x1,y1)和点(x2,y2)的距离为d，两点连线与坐标横轴的夹角为θ，那么就可以得到任意间距和任意角度的灰度共生矩阵P(i,j,d,θ)。

在实际应用中，需要在灰度共生矩阵的基础上，提取出一些既能较为准确地描述图片的纹理信息又能缩短计算时间的特征量。本文提取了以下4个养殖鱼摄食时的纹理特征量。

(1)逆差矩

(2)

(2)相关性

(3)

(3)能量

(4)

(4)对比度

(5)

从式(1)～式(5)可看出，影响纹理特征的参数有灰度级Ng、像素间的距离d和像素间的方向θ。将灰度级Ng设为8级[6]，像素间的距离设为1，根据文献[6,9]，0°、45°、90°和135°方向上的变化趋势基本相同，所以文中提取了0°方向的4个纹理特征量。

1.2.2 图像熵特征

熵可以表征体系混乱的程度，鱼之间抢食导致水面剧烈波动，波动的程度可使用图像的熵来表征，因此图像的熵也作为描述养殖鱼摄食行为的一个特征。其数学描述为：

(6)

式中，pi表示灰度值为i的像素数占全部像素数的比例。

1.2.3 基于灰度梯度共生矩阵的纹理特征

灰度梯度共生矩阵反映了图像灰度和图像梯度之间的关系，灰度梯度共生矩阵的元素Η(i,j)定义为在归一化的灰度图像F(m,n)和梯度图像G(m,n)中具有灰度i和梯度j的总象点数。以图像的总像点数归一化后得到概率为P(i,j)[10]。根据灰度梯度共生矩阵，共提取出15维纹理特征参数。

(1)小梯度优势

(2)大梯度优势

(8)

(3)灰度分布不均匀性

(9)

(4)梯度分布不均匀性

(10)

(5)能量

(11)

(6)灰度均值

(12)

(7)梯度均值

(13)

(8)灰度标准差

(9)梯度标准差

(10)相关性

(11)灰度熵

(17)

(12)梯度熵

(18)

(13)混合熵

(19)

(14)差分矩

(20)

(15)逆差分矩

(21)

2 基于支持向量机的摄食行为识别

支持向量机(SVM，support vector machine)训练摄食行为识别模型的步骤包括建立数据集、特征数据归一化及降维、支持向量机核函数选取及参数优化等。

2.1 建立数据集

采集养殖鱼摄食图像建立数据集，23条10 cm的养殖鱼生活在70 cm×30 cm×30 cm，水深15 cm鱼池中，每天早上10∶00和晚上22∶00点进行饵料投喂，实验时鱼已在鱼池生活了数月，适应了周围的环境。借鉴文献[11]，对采集的摄食图像进行标注，如表1所示。根据表1将符合无和弱两种摄食行为级别的样本作为非摄食行为样本，将符合中和强两种摄食行为级别的样本作为摄食行为样本。每个样本分别由3位养殖专业人员标注，把标注次数最多的作为该样本最终标注结果。本研究共采集650个样本，其中70%的样本作为训练集。

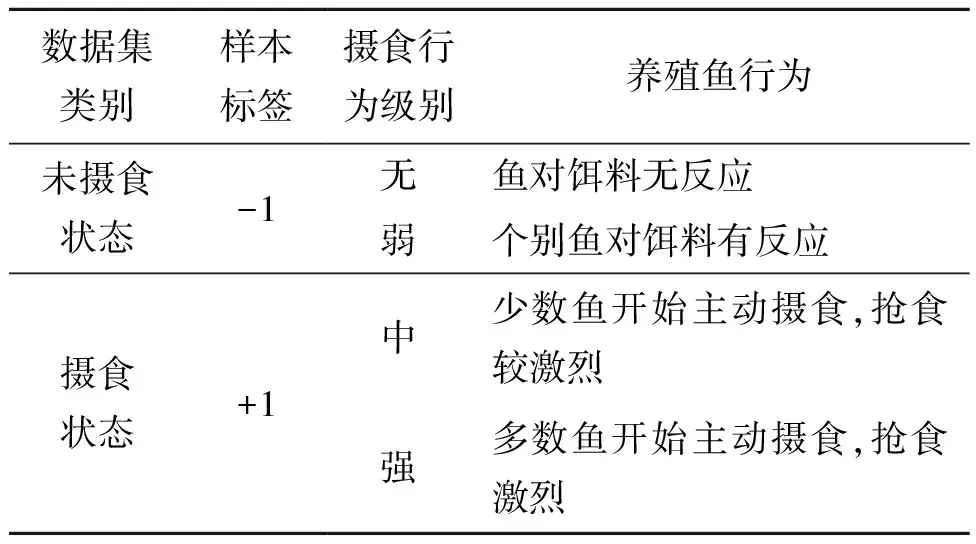
表1 数据集样本分类标准

2.2 特征数据归一化及降维

2.2.1 特征数据归一化

根据式(1)～式(21)，提取训练数据集的20维特征，对其进行归一化。选用Z-Score标准化方法，根据每个特征数据的均值μ和方差σ来进行归一化，可将训练集中的每个特征数据的均值统一变换为0，标准差统一变换为1，使用式(22)对20维特征归一化。

(22)

式中，x为标准化前的特征数据；x′为标准化后的特征数据。

2.2.2 特征数据降维

提取的20维特征中不可避免的存在特征冗余问题，特征冗余会导致计算量增大，运行时间增加。为消除冗余特征，使用主成分分析法(PCA)对特征进行降维。将原始数据特征通过映射函数映射到一个新坐标系下，在该坐标系下原始数据特征被新数据特征重新表示，新数据特征被称为主成分。

在特征数据完成归一化后，使用MATLAB中的“princomp”函数对20维特征进行降维。图2为主成分的载荷图，横坐标为主成分1，纵坐标为主成分2，黑点表示两次观测的主要值，圆圈和虚线表示载荷值。各个特征往横坐标上的投影为主成分1的载荷，往纵坐标上的投影为主成分2的载荷。从图2可以看出，对养殖鱼摄食行为识别有贡献的特征。图2为主成分累积贡献率图，横坐标表示主成分，纵坐标为累积贡献率。直方图表示各个主成分，其高度表示贡献率，即该主成分对应的方差占全部方差的比重，其反映了该主成分所包含特征数据信息量的大小，第n个累积贡献率为前n个贡献率之和，如图3中黑线所示。从图3可看出，主成分5的累积贡献率已达到98.652 2%，因此，在后面的计算中只使用5维，即特征从20维降到了5维，并且降维后的单帧运行时间与降维之前相比降低了32.3%。

图2 主成分载荷图

图3 主成分累积贡献率图

2.3 支持向量机核函数选取及参数优化

2.3.1 核函数的选取

支持向量机的核函数选择径向基函数[15]，其数学表达式为：

k(x,y)=exp(-g‖x-y‖)2

(23)

式中，g为函数参数；‖x-y‖2为两个特征向量之间欧氏距离的平方。

2.3.2 参数优化

径向基函数中两个参数影响着分类的精度，因此需要选取该训练集的最优参数。网格搜索算法(GS)是最常用的SVM选最优参数的算法，它是一种基于K折交叉验证的参数寻优方法，参数设置为：搜索步长0.5，K取5，其它使用默认参数，GS对SVM参数的寻优流程图如图4所示，按照图4，获得最优的C为8，g为0.007 812 5。

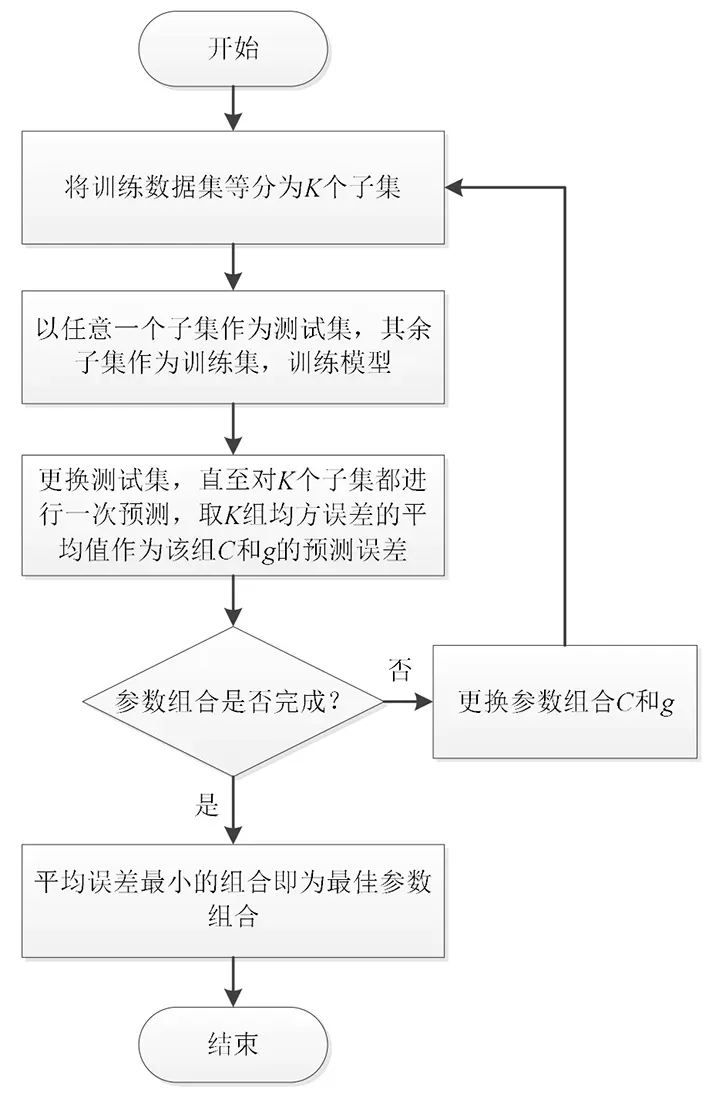
图4 GS对SVM参数的寻优过程

3 实验结果与分析

3.1 SVM模型评价指标

采用平均精确度PA、假负率FNR和假正率FPR作为SVM模型的评价指标。精确度为真正的摄食行为与分类所得摄食行为的百分比，也为真正的非摄食行为与分类所得非摄食行为的百分比，假负率为摄食行为被错误分为非摄食行为的百分比，假正率为非摄食行为被分成摄食行为的百分比。

(24)

(25)

(26)

式中，TP表示标注为摄食样本，预测为摄食样本的个数；FP为标注为非摄食样本，预测为摄食样本的个数；TN为标注为非摄食样本，预测为非摄食样本的个数；FN为标注为摄食样本，预测为非摄食样本的个数。

3.2 实验验证与分析

为了验证文中所提方法的有效性，将数据集剩下的30%样本作为测试集，使用第2节中已训练好的养殖鱼摄食行为识别模型对测试集进行识别。分别使用周超[8]中的5维特征与文中的20维特征，对测试集进行识别，并将结果进行对比，如表2所示。由表2可看出，将纹理特征增加至20维获得的PA、FNR和FPR都要优于文献[8]。

表2 两种方法的摄食行为识别结果

4 结论

1)提出的方法可有效地识别养殖鱼的摄食行为，实验结果表明，该方法的平均精确度达到了92.3%、假负率为7.34%和假正率为4.15%。

2)直接对摄食图像提取纹理特征，不但避免了养殖鱼目标复杂的前景提取，而且避免了水面波动和水花对识别带来的干扰。

3)对介于摄食和非摄食之间过渡阶段的摄食行为分类的精确度还有待提高，这也为下一步的研究指明了方向。