考虑热效应的液氢气泡生长特性研究

赖天伟 颜少航 赵琪 丁文静 刘玉涛 侯予∗

(1 西安交通大学能源与动力工程学院 西安 710049)

(2 北京卫星环境工程研究所 北京 100029)

(3 北京航天试验技术研究所 北京 100074)

1 引言

氢能凭借自身清洁、经济以及燃烧热值高的优点,在近年来得到了迅猛发展。其中液氢(LH2)因其能量密度高、输送效率高将成为氢能利用的主要形式。在液氢的储存输运过程中,由于漏热以及流动过程伴随的温度和压力变化,储罐和流体机械中经常会出现由汽化、沸腾和空化导致的气泡生成。对无限大空间中气泡的生长过程的研究是获得液氢储运过程特性的基础[1]。

为了研究不同液体工质中的气泡生长,国内外对气泡的生长过程进行了大量的理论与实验研究,特别是使用高速摄像的方法对水和氟利昂中等常温工质的气泡生长过程有了深刻的认识[2]。薄膜干涉法也被应用于研究常温工质气泡生长过程中的热边界层发展,但是由于常温工质的液汽密度较大,空化过程中的热效应对其影响较小,因此常温工质的空化模型常常忽略热效应。与常温工质不同,低温工质的热效应将对气泡的生长过程的影响较大,无法被忽略,必须做出修正。由于低温工质与常温工质热效应差别较大,因此常温工质的研究结果不能用于近似研究低温工质的气泡生长。张小斌等人对现有Schnerr-Sauer 空化模型进行修正,得到了适用于液氮等低温工质的输运空化模型[3-5]。黄彪等人对ZGB 空化模型进行了热效应修正[6],得到了混合输运的空化模型。浙江大学的朱佳凯根据热效应对液氢气泡的生长过程进行修正,并在气泡溃灭模型中考虑液体工质的可压缩性[7]。此外,边界积分法也被应用于对气泡溃灭过程中回弹过程和不规则形变,并与实验结果吻合良好[8]。但以上模型在建立过程中忽略了气泡内部的温度分布,导致其计算结果与实验结果偏差较大。

根据气泡的生长特点,基于单个气泡生长过程中的热质传递机理,全面考虑了低温介质的热效应以及热边界层对气泡生长和内部温度分布的影响,对大空间液氢气泡生长特性进行了研究。

2 过热气泡生长模型建立

独立气泡在液体工质中的生长涉及复杂的传热传质过程,应根据气泡生长过程的特点,以气泡半径生长为研究对象,如图1 所示。首先假设单个气泡处于无限大空间中,气泡生长过程中无穷远处的压力恒等于P∞,不受气泡生长影响。根据Herring[9]和Trilling[10]的假设:认为液体中音速恒等于Cl0,液体密度恒等于ρl0。根据此假设可得到考虑液体工质可压缩性的Rayleigh-Plesset 方程:

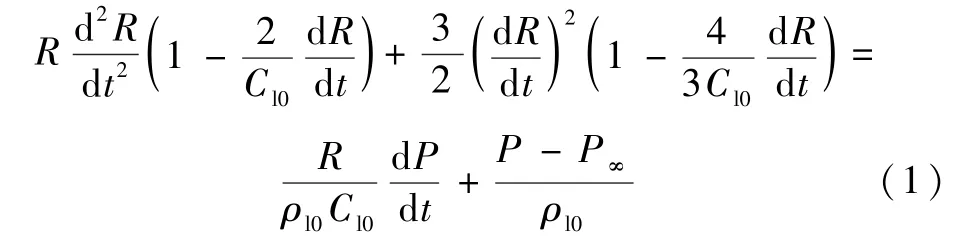
图1 单独气泡生长模型Fig.1 Single bubble growth model

式中:R为气泡半径。

当考虑液体工质的表面张力和粘度时,气泡壁面处的压力P可以表示为[7]:

式中:s为表面张力,μl为液体粘度,Pv(TB)为蒸气在气泡内温度TB对应的饱和蒸气压,PG0为初始条件下气泡内不凝气体的分压,γ为气体比定压热容和比定容热容之比。

将式(2)带入式(1)中可得到气泡生长模型的常微分方程:

气泡半径R可通过式(3)求得,其关键在于求得气泡中心温度TB。引入半无限大空间导热方程:

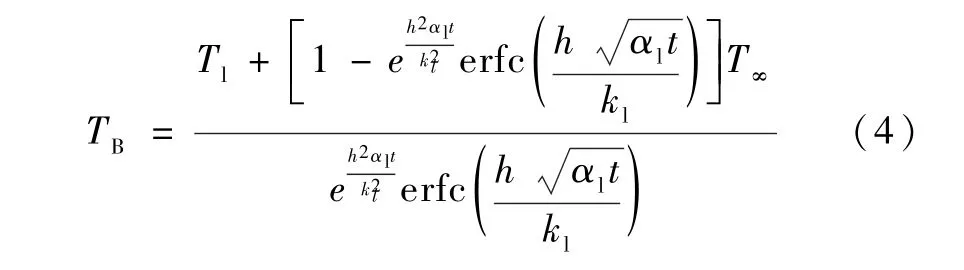
式中:Tl和T∞分别为气泡壁面处和无穷远处液体工质的温度,αl为液体热扩散系数,kl为液体热导率。h为气泡壁面液体侧的对流传热系数,可通过自然对流外掠球形的模型进行计算得到[11]:

式中:Cpl为液体定压热容。

由式(4)可得出,TB与气泡边界温度Tl相关。为求解气泡边界温度,引入本模型的第三个假设:在气泡界面外存在热边界层;而且热边界层内部只存在导热。根据热平衡条件,导入气泡的热量等于气泡的相变潜热[12],据此可得到热平衡方程:

式中:L为工质相变潜热。

对式(6)求解可得到气泡边界温度Tl,首先应当求解气泡边界处的温度梯度(dTl/dr)r=R,因此求解气泡表面至无穷远处的热扩散方程:

单个气泡的生长过程(半径变化)可通过联立求解Rayleigh-Plesset 方程(3)、半无限大空间导热方程(4)、热平衡方程(6)和热扩散方程(7)获得,求解过程如图2 所示。

图2 模型求解流程Fig.2 Model solving process

3 不同工质气泡生长过程研究

为了证明本模型的正确性,选取文献[13]的变环境压力条件下的液氮气泡生长实验结果与模型计算结果进行对比验证。文献[13]的实验中,液氮气泡最初处于饱和液氮中,随着液氮压力的缓慢降低而不断生长,其气泡半径的测量结果和由模型计算的结果对比如图3 所示。

图3 低温工质气泡生长模型验证Fig.3 Bubble growth model validation of cryogenic medium

图3 的对比结果显示,本文所提出的单个气泡一维生长模型的计算结果与实验结果的偏差不超过10%,证明了此模型的正确性。在此基础上,由于R134a 经常用作常温工质空化的研究,因此选取液氢、液氮和R134a 工质过热气泡的生长过程进行了研究和对比分析。

R134a、液氢和液氮气泡在环境压力为0.5 ×105Pa条件下,过热度为1 K 和2 K 的生长曲线分别如图4a 和图4b 所示。气泡的初始半径由Laplace-Young 方程求得。从图中可以看出,除了R134a 在过热度为1 K,环境压力为0.5 ×105Pa 工况下以外,其它工质气泡在各种工况下的半径生长曲线均存在一个由水平段到增长阶段的拐点,其对应的时间为气泡半径的临界时间tc(动力生长阶段转向热力生长阶段的分界点)。临界时间出现越早表示气泡生长过程中的热响应影响越大。通过对比可以看出,在任意过热度条件下,液氢和液氮气泡生长半径曲线的临界时间都极为接近,而R134a 气泡半径的生长曲线随过热度变化较明显。

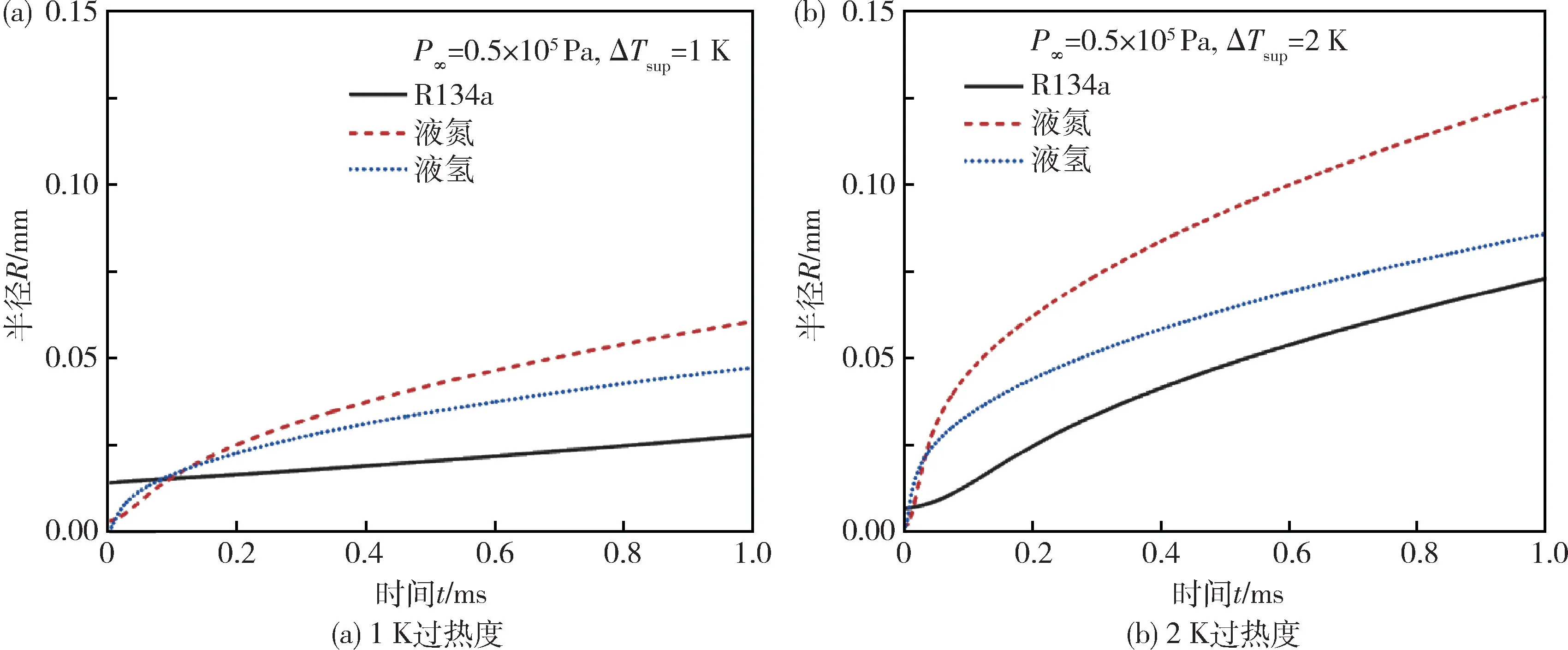
图4 0.5 ×105 Pa 压力下不同工质气泡的半径生长曲线Fig.4 Radius growth curves of bubbles of different working media at 0.5 ×105 Pa

由以上不同工质气泡半径曲线的对比可以看出,气泡的生长过程和半径的临界时间受环境压力和过热度影响。为衡量以上两因素对不同工质气泡半径临界时间的影响,进行方差分析,结果如表1 所示。对于R134a,虽然过热度对气泡生长的临界时间的影响程度大于环境压力影响程度,但其影响因数比远小于液氮和液氢;而对于液氮和液氢气泡生长的临界时间,过热度对其影响程度均为是环境压力影响程度的百余倍,两者较为接近。因此,相对过热度,环境压力对低温工质气泡生长临界时间的影响可以忽略不计。

表1 过热度和环境压力对不同工质气泡临界时间影响方差分析结果Table 1 ANOVA of influence of superheat and ambient pressure on bubble critical time of different working media

为研究导致不同工质气泡生长过程产生差异的原因,引入热标准温降ΔT针对不同工质热效应进行分析[1],定义如下:

式中:ρl和ρv分别为液相和气相密度。

根据式(8),不同工质的热效应参数计算结果如图5 所示。在环境压力为0.5 ×105Pa 时,液氮和液氢的标准温降远大于R134a,因此R134a 气泡生长过程中动力生长阶段占据较大时长,气泡半径的临界时间远大于其它两种工质;而液氮和液氢的热效应参数十分相近,两种工质气泡的生长曲线的临界时间基本重合。

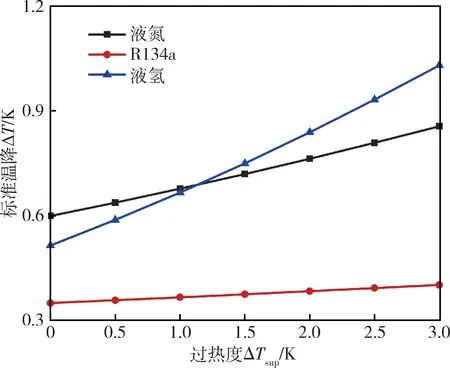
图5 不同工质的标准温降对比Fig.5 Comparison of standard temperature drop of different media

4 液氢气泡生长过程分析

环境压力为0.5 ×105Pa,不同过热度下以及过热度为1 K,不同环境压力下的液氢气泡半径生长曲线如图6 所示,并使用空心倒三角标出了气泡半径的临界时间。对比气泡生长0.16 ms 时的半径可知:在过热度恒定的条件下,环境压力的降低将使气泡半径增大;而在相同的环境压力下,气泡半径会随过热度的增大而增大。如图6a 所示:液氢气泡生长临界时间会随过热度的增加而提前;而由图6b 可看出,液氢气泡生长临界时间基本不随环境压力变化。临界时间越短代表热力生长在气泡生长过程中越重要。根据图6 中临界时间随过热度和压力的变化规律可认为,工质过热度的升高会导致气泡生长中热力学效应增强,而环境压力的变化对其热力学效应影响不大。

图6 液氢气泡的半径生长曲线Fig.6 Radius growth curve of LH2 bubbles

对液氢气泡生长1 ms 时的气泡半径和气泡生长临界时间受环境压力和过热度的影响进行方差分析,结果如表2 所示:对于临界时间,过热度的影响为环境压力影响程度的247 倍;相较过热度,环境压力对液氢气泡生长临界时间的影响基本可以忽略不计。而过热度和环境压力对气泡半径的影响则不同,环境压力对液氢气泡半径的影响程度是过热度影响程度的两倍左右。这是由于过热度直接决定了现有工况在工质P-T图中与相界线之间的距离,从而影响当前氢气的物性,而环境压力对当前工况与相界线之间的距离影响不大,因此对液氢气泡的生长过程的影响也较为微弱。

表2 过热度和环境压力对液氢气泡影响方差分析Table 2 ANOVA of influence of superheat and ambient pressure on LH2 bubbles

为研究液氢气泡生长过程中的温度分布,同一工况下不同时刻气泡内部温度的分布曲线如图7a 所示,从图中可以看出,随着时间推进,气泡中心边界的温差逐渐增大,同时高温区逐渐向气泡中心发展。由于过热度对气泡的生长过程影响较大,因此针对同一时刻,不同过热度条件下对气泡内部温度的分布进行研究。从图7b 可知,随着过热度上升,气泡内外的温差增大,但是高温区被限制在更接近气泡壁面附近。

图7 液氢气泡边界中心温差Fig.7 Temperature distribution between boundary and center of bubble in liquefied hydrogen

5 总结

根据Rayleigh-Plesset 方程,综合考虑气泡内温度分布及液体工质的可压缩性建立了单独气泡的一维生长模型,并对液氢工质气泡的生长规律和气泡生长临界时间与环境压力、过热度之间的关系进行了研究,并得到以下结论:

(1)环境压力和过热度会影响液氢单个气泡的生长速度和临界时间,过热度的影响程度远大于环境压力。相同环境压力下,工质过热度的升高会减小气泡生长的临界时间;而工质过热度恒定时,环境压力的增加对气泡半径的临界时间影响较小。

(2)标准温降是影响气泡生长过程的关键因素。气泡生长半径的临界时间随标准温降升高而减小,有相近标准温降的工质,气泡生长过程中的临界时间也较为接近。

(3)随着气泡的生长气泡内部的温差不断增大,且高温区逐渐向气泡内部发展;而过热度的增加不仅使气泡内外的温差增大,也使得气泡的高温区更加靠近气泡表面。