空间低温冷屏蔽系统分布式点蒸发制冷模型表面温度分布规律研究

张周卫 刘要森 樊翔宇 汪雅红

(1 兰州交通大学LNG 低温装备及自动化研究所 兰州 730070)

(2 兰州交通大学环境与市政工程学院 兰州 730070)

1 引言

基于高超音速飞行器要求表面温度低温100 K的指标,本文提出了分布式点蒸发“发汗”冷屏模型,并重点研究三角形、正方形、圆形以及蜂窝形发汗冷却结构在不同几何形状及分布方式时表面温度的分布规律等问题。

2 系统模型构建

构建高超音速飞行器整体模型(图1),根据顶部锥形外形,建立边长为40 cm 的等边三角形单元传热模型。模拟冷屏内侧为自增压液氮容器时,发汗冷却通道不同几何类型、数目以及间距对特定环境参数下模型的温度分布规律(图2)。通过改变内部发汗点的单元几何结构,如三角形、圆形、正方形及蜂窝形等,在保持发汗冷却通道几何结构总面积不变的情况下,基于点个数为3、4、5 及6 时进行模拟。此外在保持总面积和几何结构数量相等的前提下,改变点间距分别为1 cm、3 cm、6 cm 及10 cm 时进行模拟。

图1 高超音速飞行器整体模型图Fig.1 Overall diagram of hypersonic vehicle

图2 单元模型图Fig.2 Element model diagram

液氮在冷屏蔽内的流动过程控制方程包括连续性方程、动量方程以及能量方程。

连续性方程:

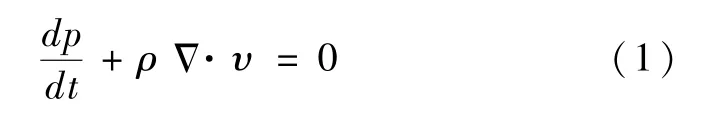
动量方程:

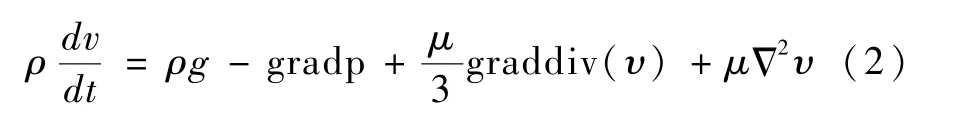
能量方程:

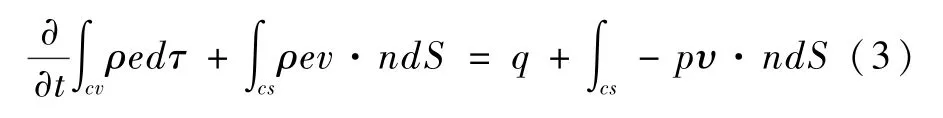
式中:ρ为密度,kg/m3;t为时间,s;v为速度,m/s;p为压力,Pa;μ为粘度,Pa·s;cv为控制体;cs为控制面;e为内能,J;S为流体通过截面积,m2;q为系统吸收的热,W。

“巧妇难为无米之炊”，军事基础训练的展开自然离不开训练场地器材保障，院校训练场地器材使用频率高，更容易发生松动、破损情况，进而诱发训练伤害事故。首先，在组织训练前，组织者要亲自对场地器材进行检查，查看是否存在安全风险。其次，要保证场地器材的质量，质量合格方能进入校园使用；再次，教学保障部门要定期对场地器材进行检查与维护，并对损坏之处进行更换；最后，要教育学员像爱惜自己的物品一样爱惜训练场地设施，加强对器设施的规范化管理。

冷屏蔽系统在运行过程中所受到的热流量主要包括地球热辐射、环境热辐射、太阳能辐射、大气反射等。

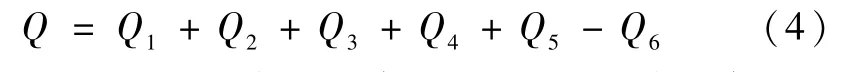
式中:Q1表示环境热辐射,Q2表示地球辐射,Q3表示太阳能辐射,Q4表示太阳能反射,Q5表示稀薄气体加热,Q6表示饱和蒸汽节流后的冷量。其中各参数的计算公式如下:

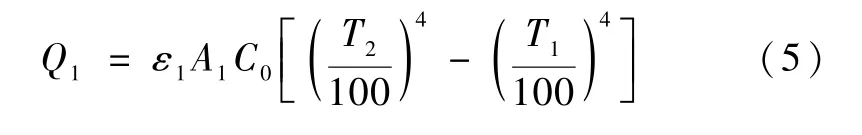
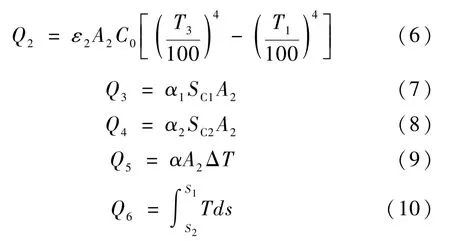
式中:表面发射率ε1=0.06;A1为模型外表面积;C0为黑体辐射常数,C0=5.67 W/(m2·K4);T1=77.355 K;T2=257 K;A2为模型最大截面面积;T3=300 K;α1取传热条件最坏下的吸收率,即α1=1;太阳能辐射强度Sc1=136 7 W/m2;α2取传热条件坏时的太阳能吸收率,即α2=1;太阳能大气反射强度Sc2=408 W/m2;α为稀薄气体加热系数,由于接近真空,故取α≈0;s1、s2为系统压力及环境压力下制冷剂对应的熵值。

在中段运行时空间冷屏表面所接受的外来热流量为3 000 W/m2。针对空间冷屏内侧与外侧分别采用第一类和第二类边界条件,即分别给定温度和热流密度。

3 模型简化及数值模拟分析

由于空间冷屏内壁可通过液氮的蒸发保持恒定温度,故将模型简化为边长为40 cm 的等边三角形,冷屏内部几何结构的壁面厚度取为0.1 cm,能够更好的保证符合实际预想结果。简化后的内部单元传热模型如图3 所示。

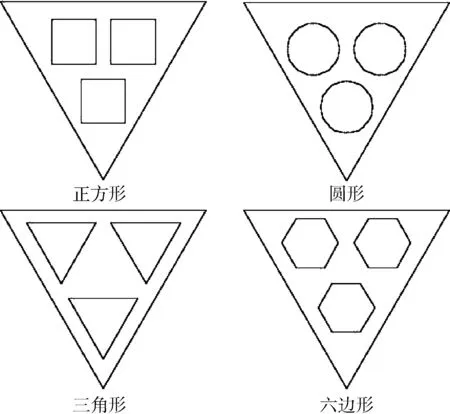
图3 单元内部模型Fig.3 Cell internal model

空间冷屏系统内部充满液氮的空间可通过填充大孔径无吸附能力的毛细材料防止液氮在飞行过程中的晃动。通过模拟不同结构及几何结构之间的间距,对比其外表面温度的变化。采用四面体网格对计算区域进行了划分,并进行网格无关性验证,选取网格数量为589 450 个,所选取的几何结构在不同相对数目下的几何参数见表1。

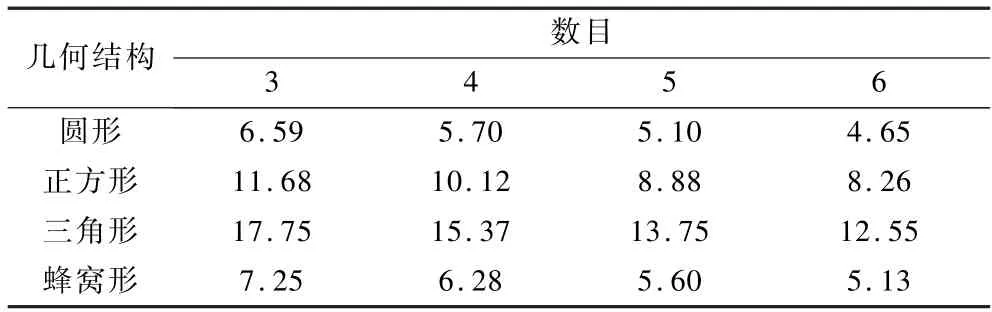
表1 不同几何结构数目所对应的边长Table 1 Side lengths corresponding to different numbers of geometric structures

采用Fluent 进行数值模拟,当传热稳定之后,使冷屏外表面的温度分布、最高温度与平均温度,能够满足红外探测的最低要求即小于110 K。

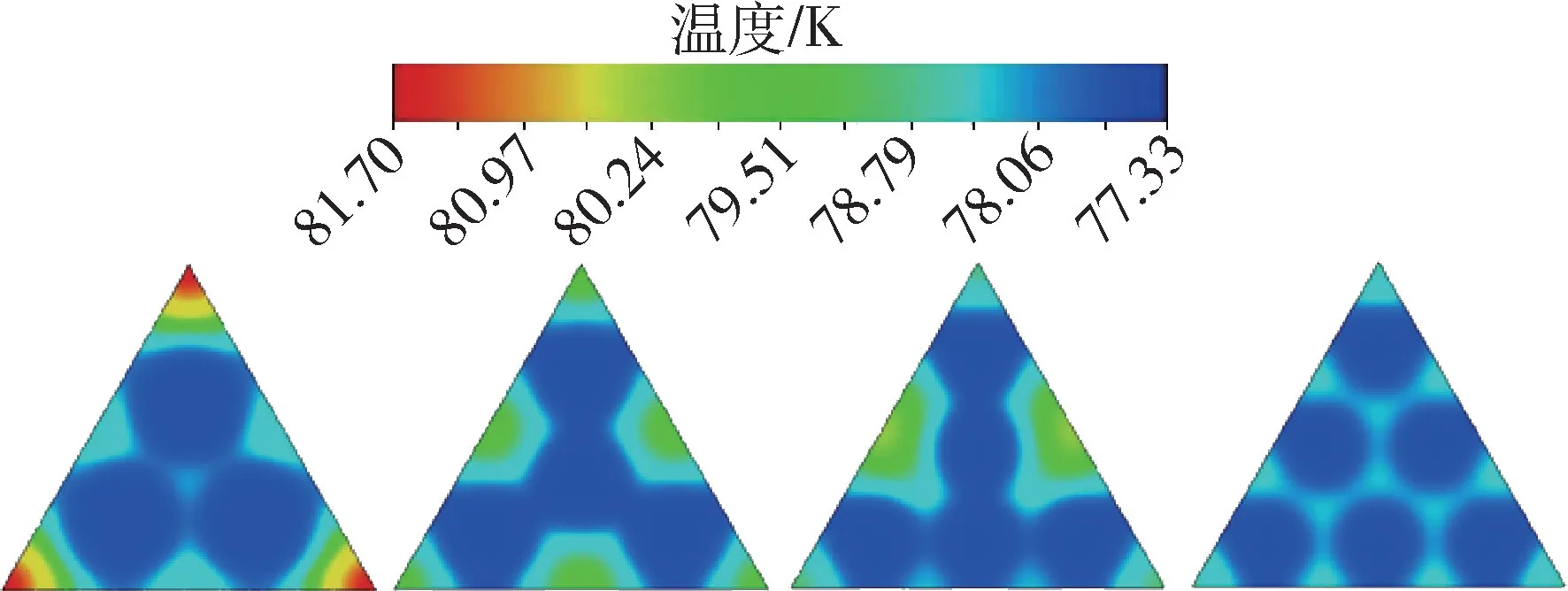
图4 圆形结构数目变化温度分布图Fig.4 Temperature distribution diagram of number change for circular structures

制冷剂通道为圆形结构,且在总面积不变的情况下,当数目发生变化时的温度变化趋势为:在数目最少时,最高温度出现最大值,在数目为6 个时,温度较低且分布较为均匀。

当冷屏系统达到稳定之后,在保持内部几何结构表面积不变的前提下,由图5 可得出随着通道数目的增加,冷屏外表面温度整体呈现下降趋势,但对于正方形和三角形两种结构类型,分别在3 个和4 个时温度呈现上升。这是由于4 个三角形通道时能够覆盖的表面更加全面,仅在单元模型最下端有一处温度略高,其余位置温度分布最为均匀(见图7c)。当为4个正方形通道时,由于顶端间距较大且中部两侧温度也高于其余位置,故其平均温度最高(见图7b)。其中平均温度最低的为4 个三角形几何结构为77.74 K,平均温度最高的为4 个正方形几何结构为78.31 K。由图6 可得出正方形的最高温度变化在4 种几何结构中最高,其中3 个正方形几何结构的最高温度最高为82.56 K,4 个三角形几何结构的最高温度最低为78.79 K。同理由于正方形几何结构顶部距顶点最远,故其拥有相比于其他几何结构更高的最高温度(见图7a),而4 个三角形几何结构中每个几何结构据单元模型边界距离差距较小,故最高温度小于其它几何结构。

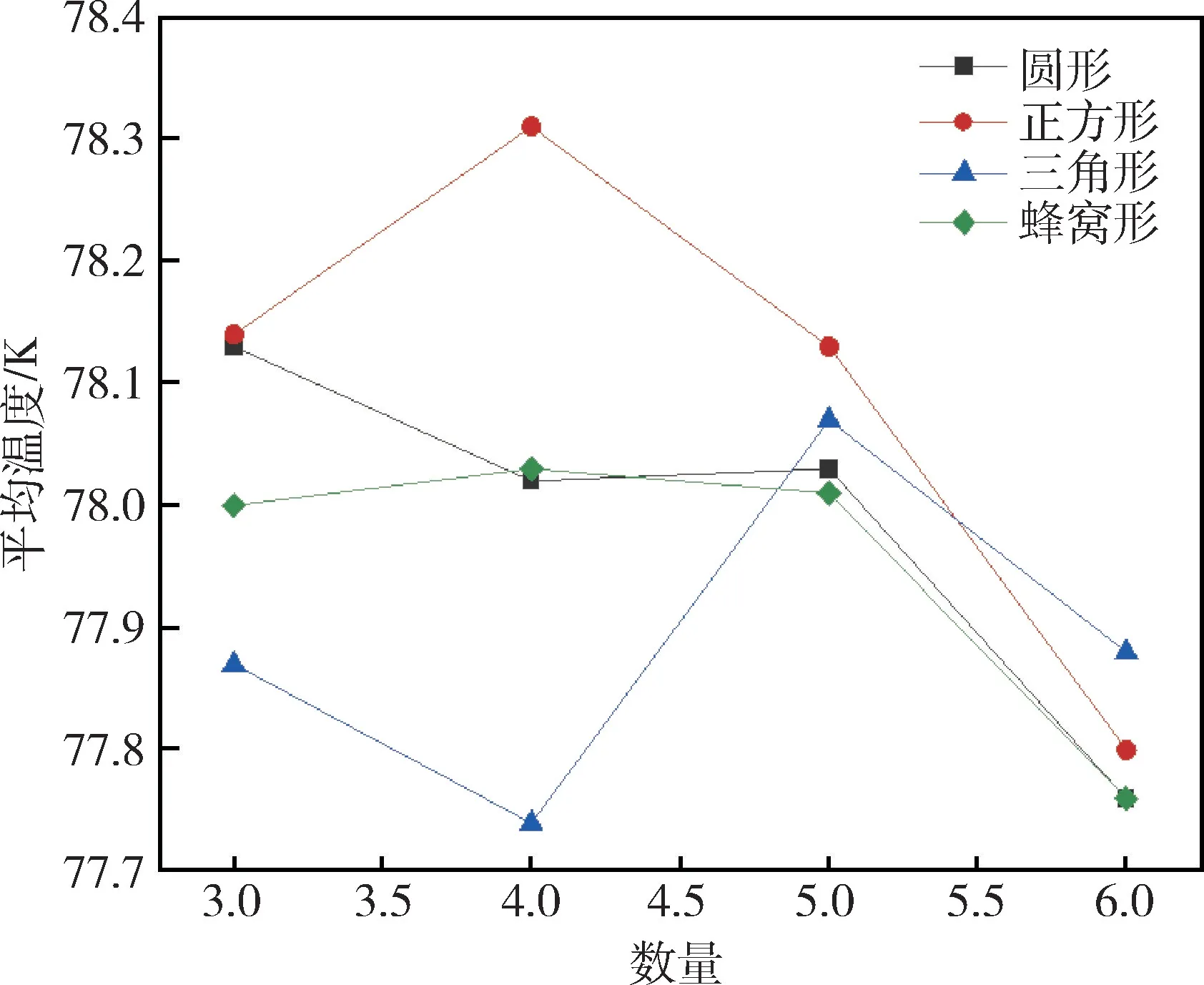
图5 变数目后平均温度Fig.5 Average temperature under different number

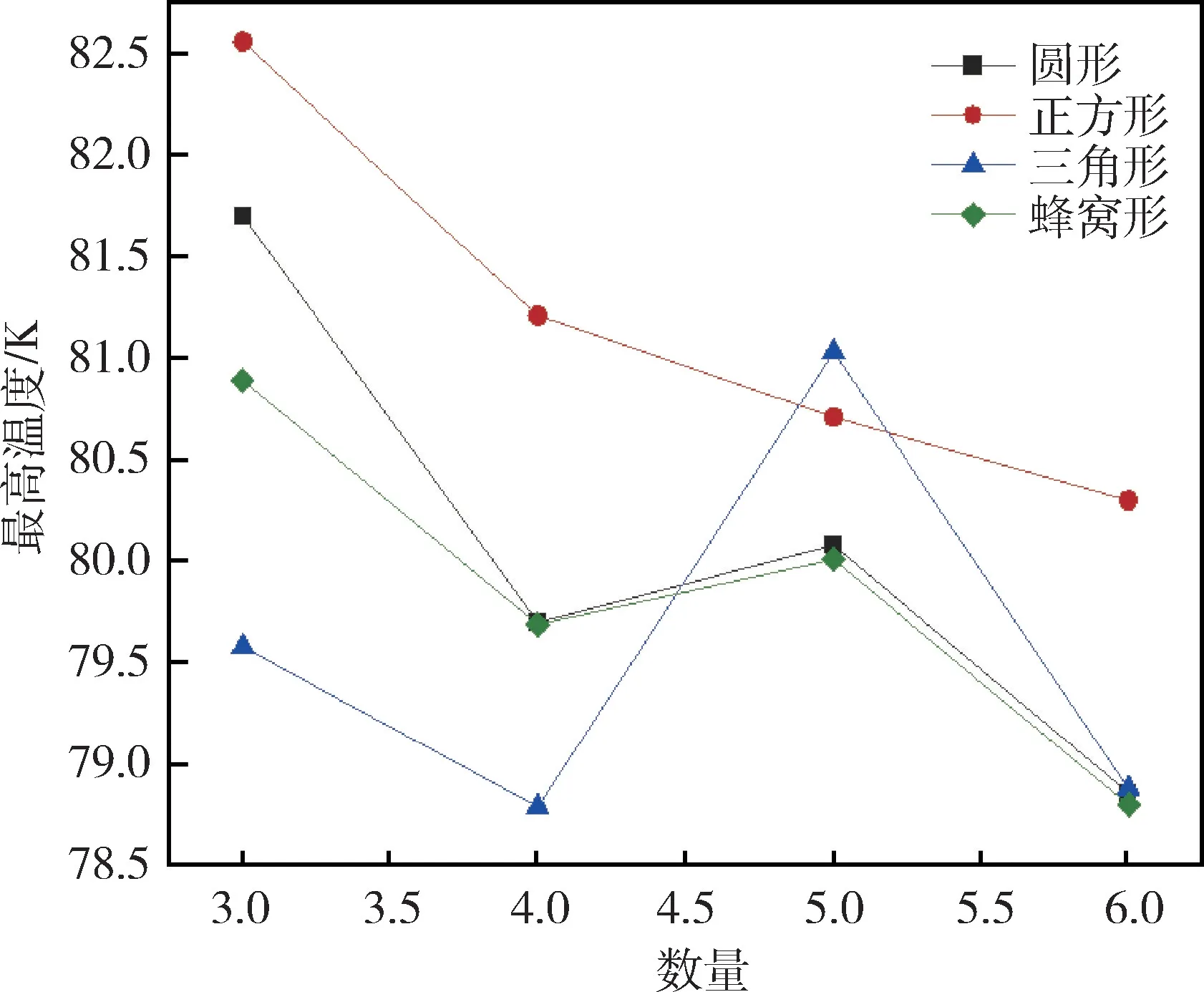
图6 变数目后最高温度Fig.6 Maximum temperature under variable number

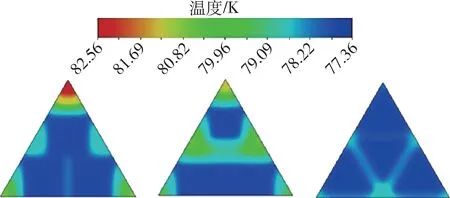
图7 典型模型温度分布图Fig.7 Typical model temperature profile

对于发汗冷却通道结构之间的间距不同时,其尺寸参数分别为:正方形结构边长为8.86 cm;圆形结构半径为5.0 cm;三角形结构边长为13.46 cm;蜂窝形结构边长为5.5 cm。

在点蒸发面积相等时,通道间距发生改变时表面的温度分布也会发生变化。在间距最大和最小时,温度分布皆略显不均匀,且最高温度出现的位置随着间距的增大逐渐从顶点转移至中心位置。

当冷屏系统处于稳定状态时,外界摄入的热流密度均被内部液氮的蒸发吸热完全平衡,其外表面温度趋于稳定,其外表面最高温度及平均温度不再发生变化。由图9 可以看出外表面的平均温度随着几何结构间距的增大先减小再增大,平均温度最大出现在间距为1 cm 和10 cm 处,这是由于间距为1 cm 时其位于单元模型中央,距离端点处较远,故温度较高,而间距为10 cm 时,几何结构大多位于单元模型边界处,中间位置温度较高,相比间距为3 cm及6 cm 而言几何结构分布较为不均匀。同时由图9 可知平均温度最小的为间距3 cm 的三角形几何结构中为78.54 K(见图11c);最大出现在间距为10 cm 的三角形几何结构中为80.52 K(见图11b)。由图10 可知模拟的几种几何结构中正方形和圆形随着间距的增大其最高温度逐渐减小,而三角形和蜂窝形的最高温度皆是随着间距的增大先减小再增大,这是由于相同面积的圆形和正方形在冷屏表面所占比例较为均匀,受到外界热流密度加热时,内部的液氮能够更好的对外表面进行降温,而三角形及蜂窝形由于间距较小时距冷屏边缘位置较远,而当间距较大时,距冷屏中心位置较远,不能均匀的冷却冷屏表面的温度。最高温度最小的是间距为3 cm 时的三角形结构为80.56 K,其模拟如图11c 所示,最高温度最大的时间距为1 cm 的正方形结构为86.56 K(见图11a)。

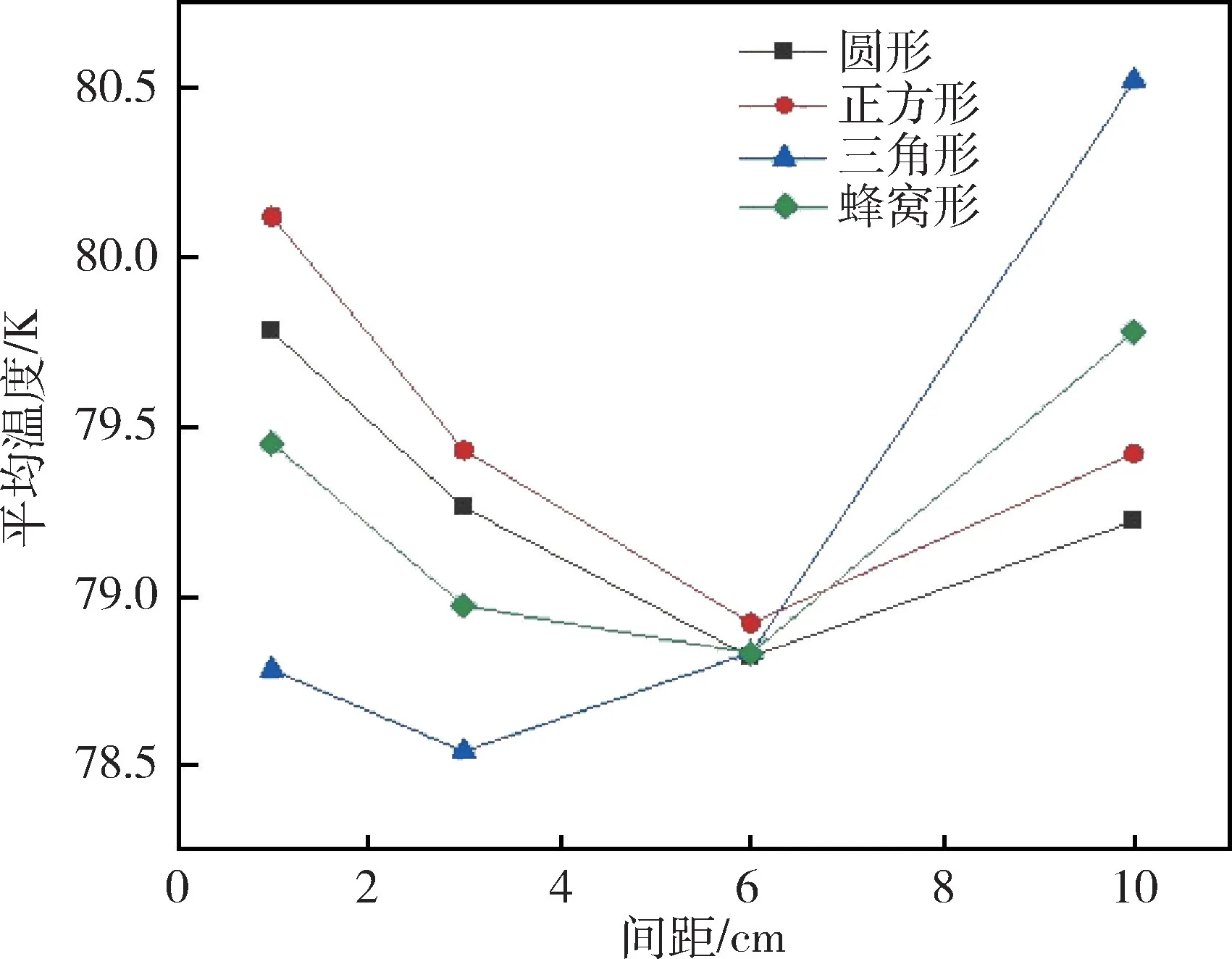
图9 变间距后平均温度Fig.9 Average temperature under variable spacing

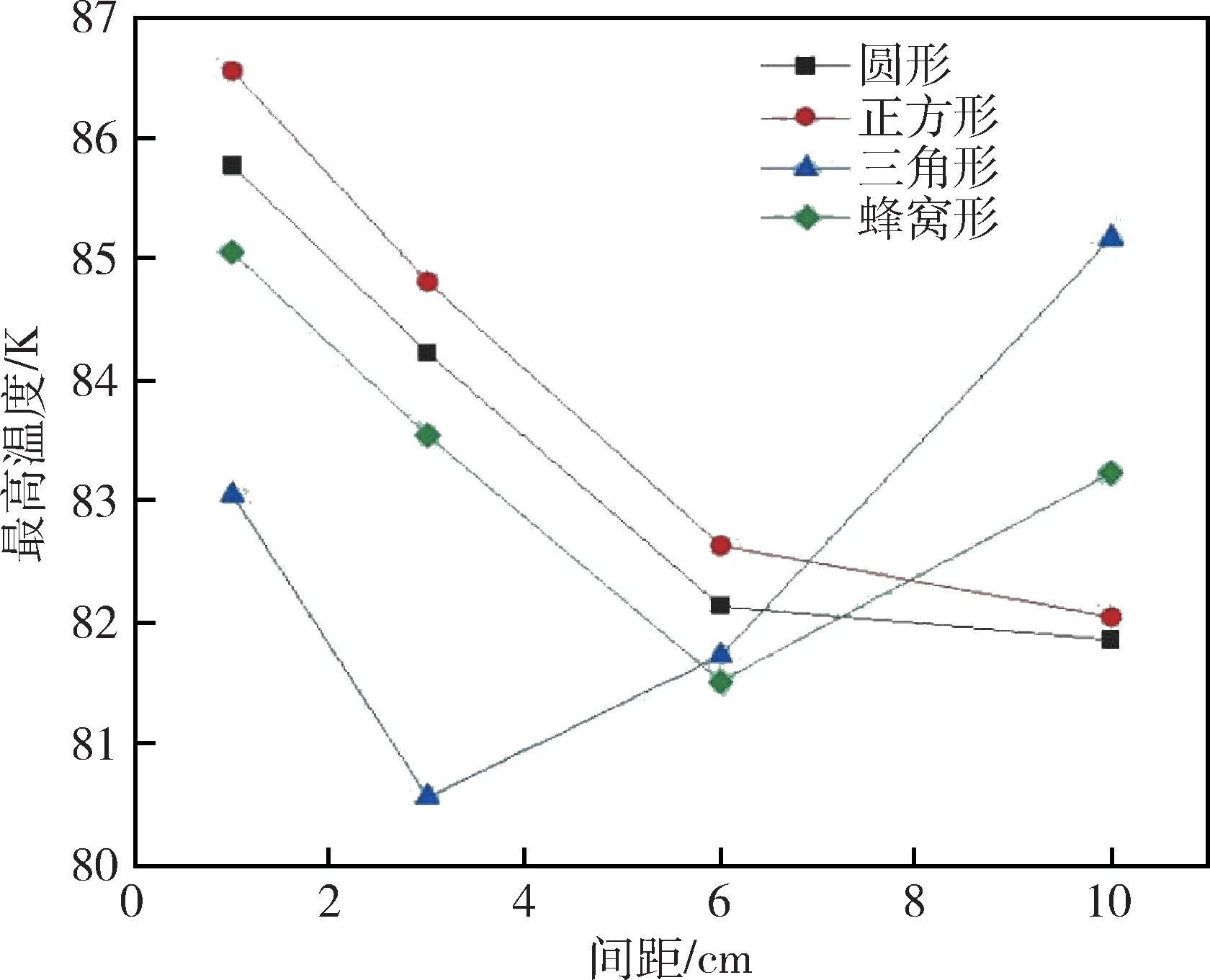
图10 变间距后最高温度Fig.10 Maximum temperature under variable spacing

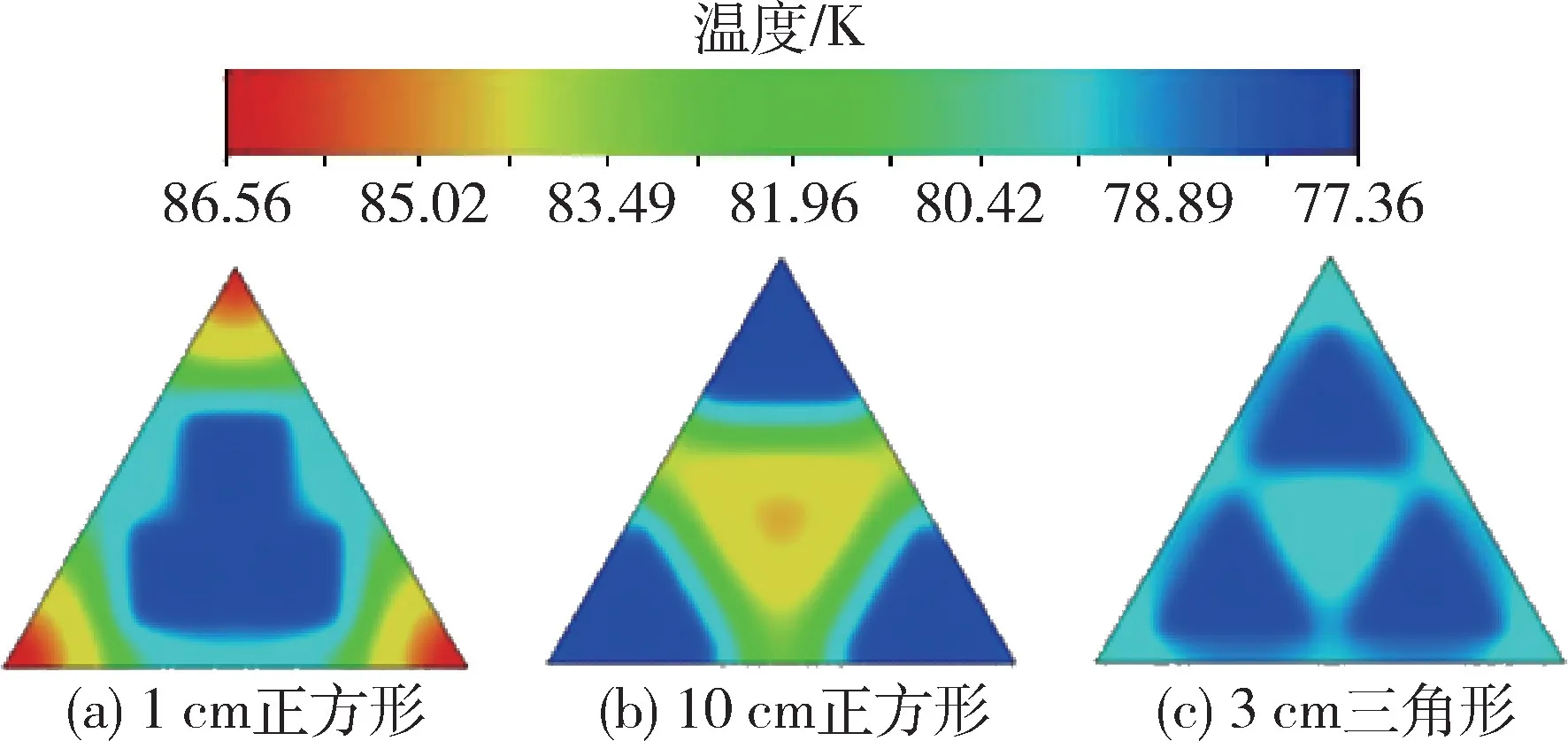
图11 变间距典型模型温度分布图Fig.11 Temperature distribution diagram of typical model with variable spacing

4 实验

图12 为实验的流程图,实验过程为受热面受到石英灯阵恒定热流密度的加热,其下表面的温度迅速升高,在上表面发汗冷却通道中通入液氮,使液氮在通道中完成进行相变制冷,达到冷却受热面的效果。由于试验面为轴对称模型,因此受热面上热电偶测点布置,除了在各顶点布置测点外,还在轴线和一条边线上进行了测点的布置。实验采用的石英灯为定制石英灯,全长55 cm,有效加热长度为40 cm,额定功率为1 500 W,并使其达到受热面的热流密度保持恒定。本次实验验证对圆形和正方形发汗冷却通道的数目和间距变化进行了研究。

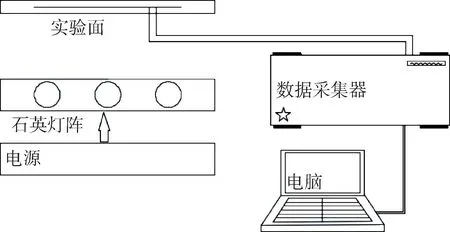
图12 实验流程图Fig.12 Experimental flow chart

图13 为实验台进行实验图,图14 显示了圆形、正方形通道个数变化时实验和数值模拟最高温度的对比,图15 显示了圆形和正方形通道数目相同间距不同时实验和数值计算的对比,图16 显示了轴线上的实验与数值计算温度分布对比。

图13 实验布置图Fig.13 Experimental layout

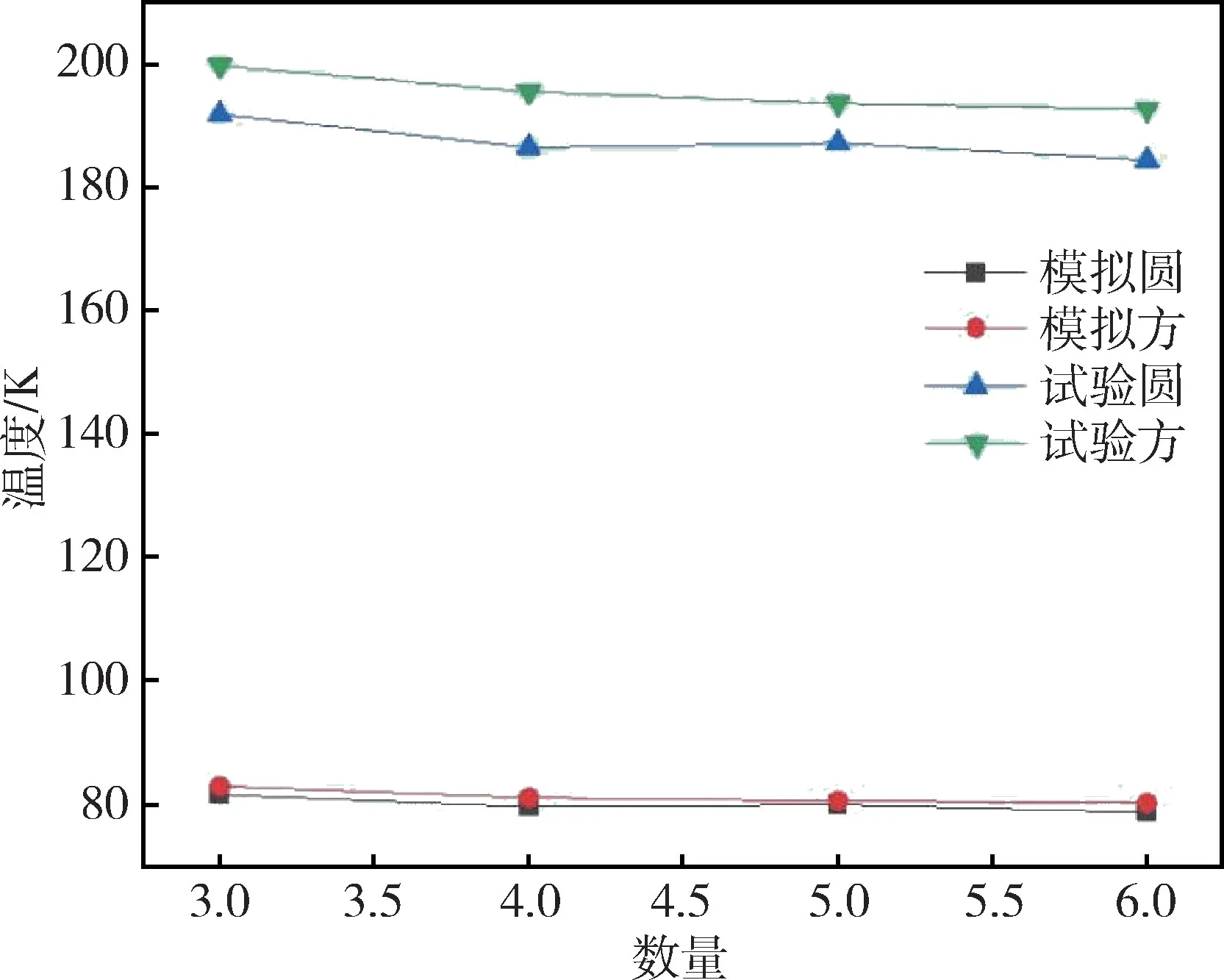
图14 发汗冷却通道类型及数量实验验证Fig.14 Experimental verification of type and number of sweat cooling channels

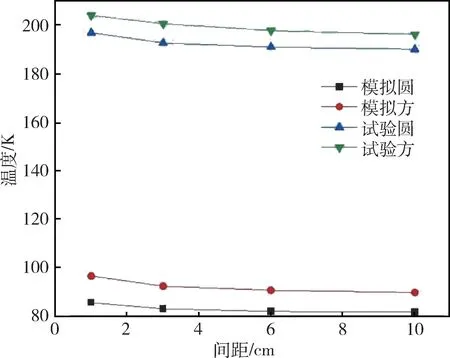
图15 发汗冷却通道类型及间距实验验证Fig.15 Experimental verification of sweat cooling channel type and spacing

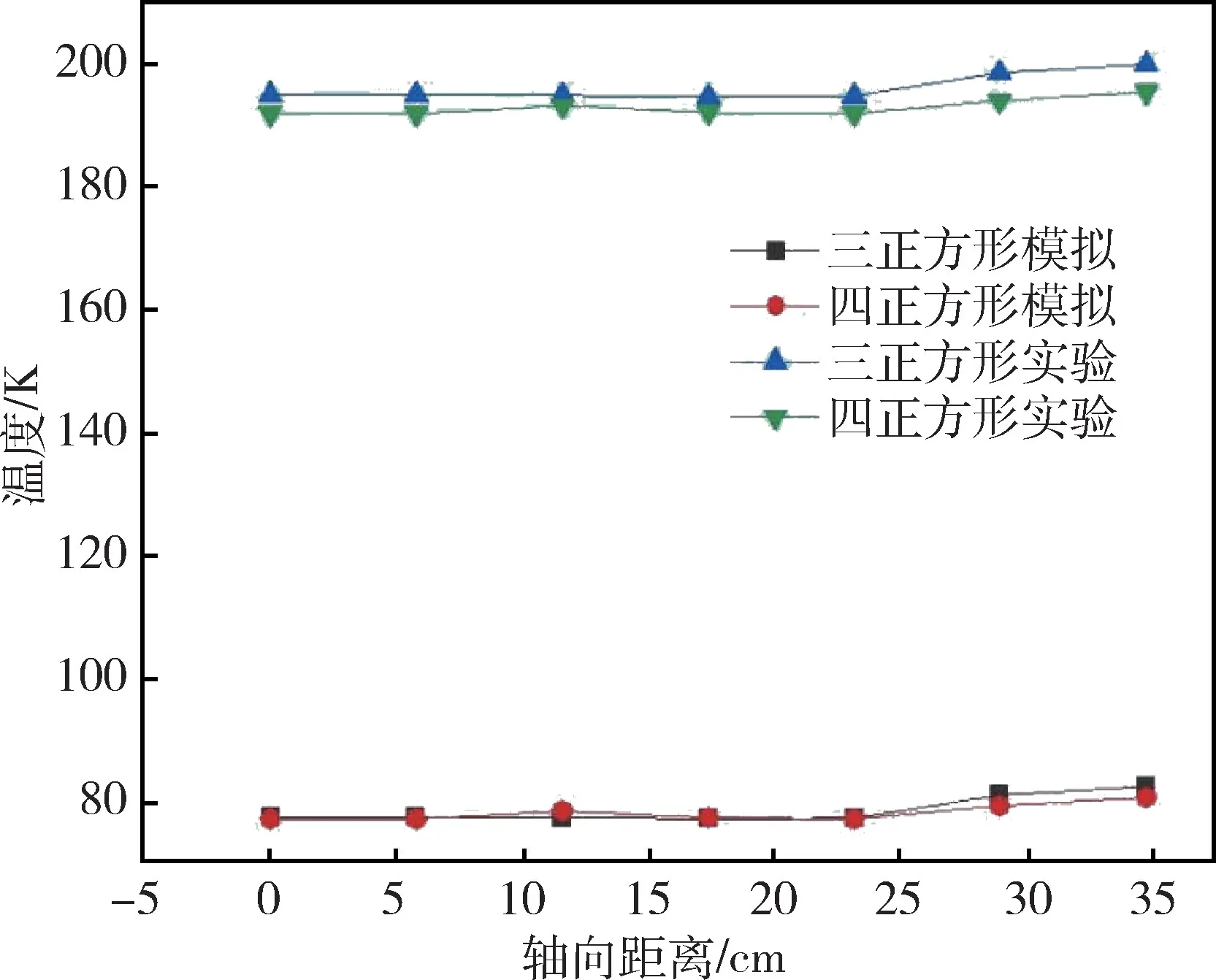
图16 轴向温度实验验证Fig.16 Axial temperature experimental verification

根据实验和数值模拟所得数据的对比可知:实验所得温度的变化规律与数值模拟所得温度的变化规律相似,在单元模型发汗冷却通道总面积相等时,改变结构种类与数量,空间冷屏外表面最高温度整体随着数量的增加而降低,同时圆形结构相较于方形结构效果会更好。

通过对比圆形和方形结构在数目变化时的实验和模拟数据可得,在发汗冷却通道面积相等的前提下,随着通道之间间距的增大,冷屏外表面的最高温度随之减小,且圆形结构效果好于方形结构。图16展示了沿轴线热电偶测点位置模拟和实验温度对比图。由于本实验是在地面完成的,与空间环境存在一定的区别,主要包括空气的热对流、热传导以及大气环境的热辐射,因此实验所测出的数据与模拟数据存在一定的误差,但温度沿轴向的变化趋势一致。

5 讨论

由数值模拟和实验验证可知,当改变发汗冷却结构类型、数量以及间距时,冷屏外表面的温度也会随之发生变化。因此在实际应用中需要通过对比,选取合适的参数以使所需的液氮量和冷屏表面温度均为最低。

当冷却点类型相同,改变数目时,正方形和蜂窝形外表面的平均温度随数目变化呈现先增大后减小的趋势,在6 个时取得最小值,分别为77.8 K 和77.76 K。这是由于正方形和蜂窝形随着数量的增多,距通道最远处的温度先增大后减小,在6 个时发汗点之间的间距最小且顶点处的温度最低;当冷却点类型和数目相同,改变其间距时,四种结构的外表面平均温度随间距的增大均呈现先减小再增大的趋势,由于间距为1 cm 和10 cm 时,发汗点之间的距离太小或太大,导致边缘处或中心处的温度较高,从而使整体的平均温度较大。但冷屏外表面的最高温度随间距的增大,不同结构之间的分布有所不同,其中圆形和正方形皆是随着间距的增大最高温度不断减小,在间距为1 cm 处取得最大值,分别为85.78 K 和86.56 K,在10 cm 处取得最小值,分别为81.86K 和82.05 K。这是由于在间距最小时模型顶点处的温度最高,且距液氮发汗点的位置最远,在间距最大时,温度最高出现在中心处,此时发汗点距中心距离相对较近,因此温度较低。三角形和蜂窝形随着间距的增大最高温度先减小后增大,由于三角形的结构和所取模型结构相似,因此对顶点处的影响较大。温度最高出现在间距10 cm 处为85.18 K,间距为3 cm 时中心位置及顶点距发汗点间距较小,取得最小值为80.56 K。以上实验结果均能满足表面温度低于100 K 的要求,可使表面红外辐射强度低于0.5 W/m2。

6 结论

通过对分布式点蒸发制冷模型的数值模拟和实验验证的研究,在满足表面温度低于100 K 及红外辐射强度低于0.5 W/m2的指标要求下,掌握了其外表面不同几何结构制冷模型的温度分布规律分布式点蒸发点的具体结构及排列方式。

(1)提出了空间冷屏系统的分布式点蒸发制冷模型,并建立了相应的物理模型。获得了分布式点蒸发中结构类型、数目及间距对表面温度影响的规律。

(2)掌握了飞行中段空间冷屏制冷过程的点蒸发制冷结构的设计方法,为超音速飞行器空间制冷方式提供了新的思路并进行了实验验证,给出了具体的实验参考数据,对建立空间冷屏主动制冷模型具有参考作用。

(3)通过改变结构类型、数目及间距可改变表面的温度,在数目较少和间距较小时,三角形结构制冷效果较好;数目较多时,圆形和蜂窝形结构制冷效果较好;间距较大时,圆形和正方形结构制冷效果较好。