Order-Preserved Preset-Time Cooperative Control:A Monotone System-Based Approach
Boda Ning,,, and Qing-Long Han,,
Abstract—This paper is concerned with order-preserved preset-time cooperative control of multi-agent systems with directed graphs. A novel monotone system-based approach is proposed to preserve the initial order of agents while guaranteeing the preset-time state agreement. Specifically, three different distributed controllers together with sufficient conditions are designed to realize leaderless consensus, leader-following consensus, and containment control, respectively. The proposed controllers facilitate preset-time deployment of agents in practical scenarios with collision avoidance requirement. Comparison studies through a numerical example are carried out to illustrate the effectiveness of the proposed controllers.
I. INTRODUCTION
RECENT advances in wireless communication and development in high-performance microcontrollers have given rise to cooperative control of multi-agent systems that,compared to a single agent, allows each agent to communicate with neighboring agents to fulfill complex tasks with increased efficiency, robustness, and scalability [1]–[5]. Among several research topics of cooperative control, consensus is a key and fundamental one, which aims to achieve state agreement by using only local information [6]–[10]. Another interesting topic is consensus of a team of agents with respect to one leader, whose state trajectory is independent of all other agents and thus is tracked by all others [11]–[13]. In the presence of multiple leaders, containment control is further explored in [14]–[17], where follower agents move into a convex hull that is spanned by leaders.
Convergence rate is a key index to evaluate the designed controllers [6]–[15]. In some practical scenarios such as tracking and intercepting a missile, it is favorable to accomplish cooperative tasks with faster convergence rates.Following this line, finite-time cooperative control has attracted significant research attention [18]–[21]. To further lift the dependence on initial conditions, results of cooperative control in the fixed-time framework have been emerging since the establishment of fixed-time stability [22], see work in [23]and [24]. However, most of the fixed-time control strategies have two shortcomings. First, the estimate for the settling time bound is conservative due to the commonly used fractional power-based controllers. As a result, the conservative estimate fails to provide usable system information in practical scenarios. Second, there exists a large initial control input by using fixed-time controllers with a fractional power that is larger than one. Such a large input can either destroy physical motors or cause a saturation issue that undermines system performance. In order to derive an accurate bound for the settling time with acceptable input magnitude, time-varying functions have been used to realize prescribed-time cooperative control [25]–[29]. For example, a time-varying scaling function-based leader-following controller is proposed in [25] with the controller being continuous everywhere. In[26], time-varying gains (defined in a specific time frame) are utilized to realize leaderless consensus for double-integrator systems. In [28], new controllers based on time-dependent functions are designed to achieve consensus while exploring practical scenarios, i.e., inaccurate initial states and unexpected disturbances.
Most of the aforementioned cooperative control results are obtained without considering the possible collision among interacting agents. As a result, the existing controllers in[25]–[29] can no longer work effectively when agents collide with each other during the coordination process. To address this concern, a class of state-dependent repelling weights are designed to replace the fixed weight between neighbouring agents [30]–[32]. For example, in [30], swarm aggregation with collision avoidance is achieved for multiple kinematic robots by using a repulsive potential field-based controller. In[31], both aggregation and dispersion are investigated for mobile agents with maximum and minimum node degree constraints. In [32], a connectivity control method integrating the collision-avoidance controller is proposed to realize formation control for nonholonomic wheeled mobile robots.Considering the velocity alignment, repulsive weights are further utilized in collision-free flocking control [33]–[35].Different from the repulsive weights-based approach, in [36],it is shown that if agents are initially positioned in a clockwise(or counterclockwise) order, then the order will be preserved over time by using a cyclic pursuit controller, and thus guaranteeing collision-free coordination. More recently, a monotone system-based strategy has been developed in [37] to preserve the order of networked agents such that no collision occurs during the consensus process. As pointed out in [37],order preservation is a kind of invariants, which can better predict the transient behavior of agents. Based on the monotone systems theory, order preservation also has been investigated in [38], where an integral excitation condition is proposed to guarantee the exponential stability of switched homogeneous positive systems, and in [39] where desired circle formations are formed when each agent interacts with its two immediate neighbors.
Compared with the repulsive weights-based approach used in [30]–[35], the monotone system-based strategy does not add extra terms (such as potential fields) on top of cooperative controllers. Thus, engineers can focus on the controller design to meet the requirement of different cooperative tasks.Motivated by the aforementioned observations, we aim to achieve order-preserved preset-time consensus in this paper by using a monotone system-based approach. Under directed graphs, a new distributed controller together with sufficient conditions is proposed to realize leaderless consensus. It is theoretically proved that the coordination is collision-free over time, while the state agreement is realized in preset-time. In the presence of one and two leaders, respectively, leaderfollowing consensus and containment control are further investigated, respectively. The designed order-preserved preset-time cooperative controllers have advantages in collision avoidance and accurate response, which have the potential to be implemented in practical scenarios such as survivor searching in earthquake and missile interception in military.
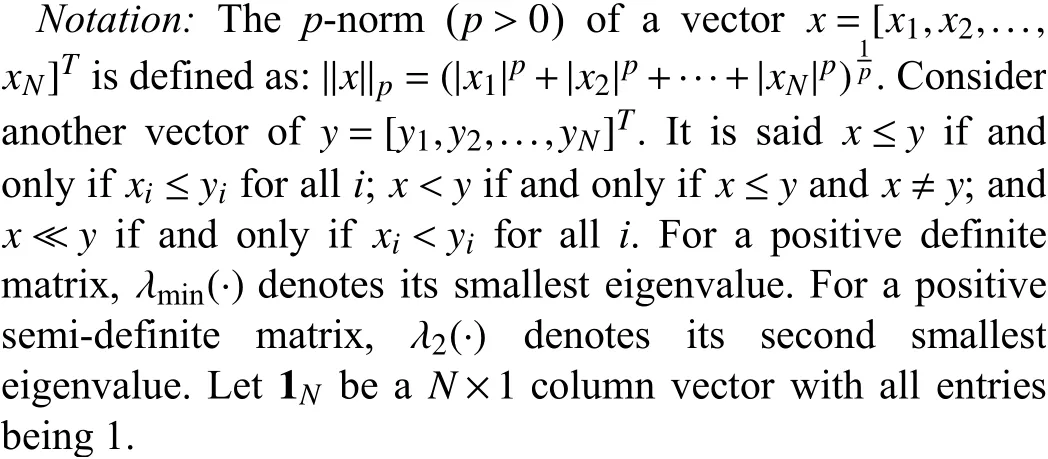
II. PRELIMINARIES AND PROBLEM FORMULATION
A. Graph Theory


B. Monotone Systems
Some definitions and lemmas from monotone systems theory are presented in this section, which are summarized based on results in [36], [40].

C. Problem Formulation



D. Time Base Generator

III. MAIN RESULTS

A. Leaderless Consensus



B. Leader-Following Consensus
Consider a dynamical network that is comprised ofN+1 agents. The dynamics of theith agent,i∈N ∪{N+1}, can be described by


C. Containment Control



IV. A NUMERICAL EXAMPLE
In this section, a numerical example is utilized to demonstrate the effectiveness of the proposed controllers. We consider a multi-agent system with four agents, i.e.,N=4.
A. Performance of the Proposed Controller

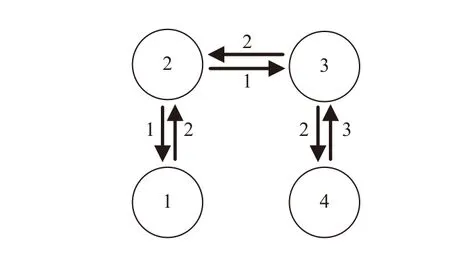
Fig. 1. Communication topology.
withtf=4 s . Furthermore, choose δ =0.0001. Initial conditions of four agents are set asx1(0)=-520,x2(0)=-210,x3(0)=140, andx4(0)=360 , satisfyingx1(0)<x2(0)<x3(0)<x4(0).
Implementing controller (7) withN=4, the results are presented in Figs. 2–4. Particularly, in Fig. 2, the consensus is achieved at 4 s with collision-free trajectory. To show the collision-free coordination more clearly, the state difference between every two consecutive agents is shown in Fig. 3,where the positive state difference confirms the collision-free coordination.
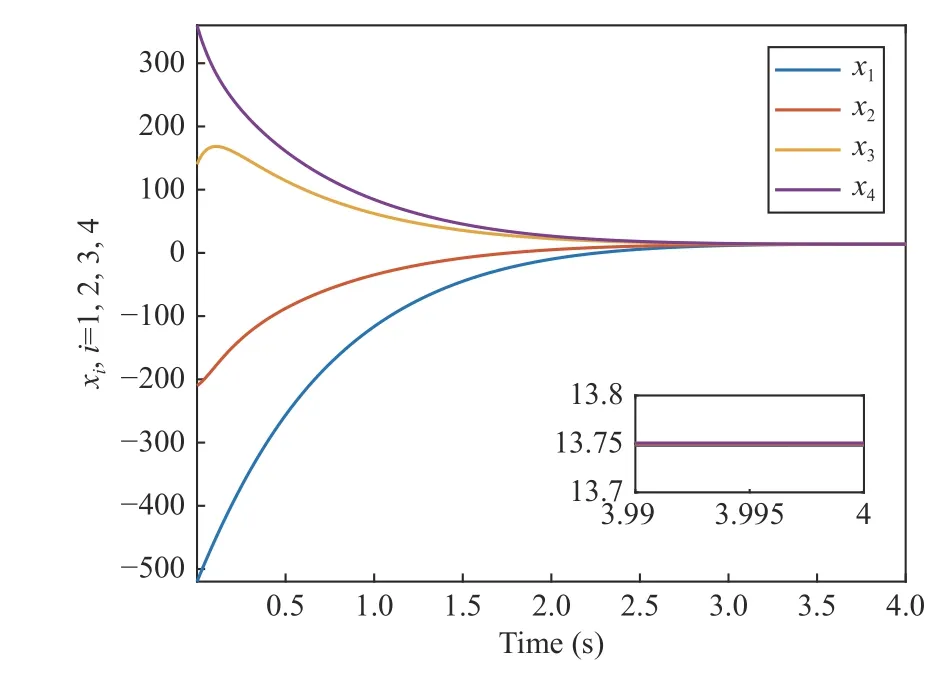
Fig. 2. State trajectories by using proposed controller (7).
Fig. 3. State differences by using proposed controller (7).
B. Comparison Studies
In order to make a comparison, we change the directed graph pattern (shown in Fig. 5) with the associated matrixA being
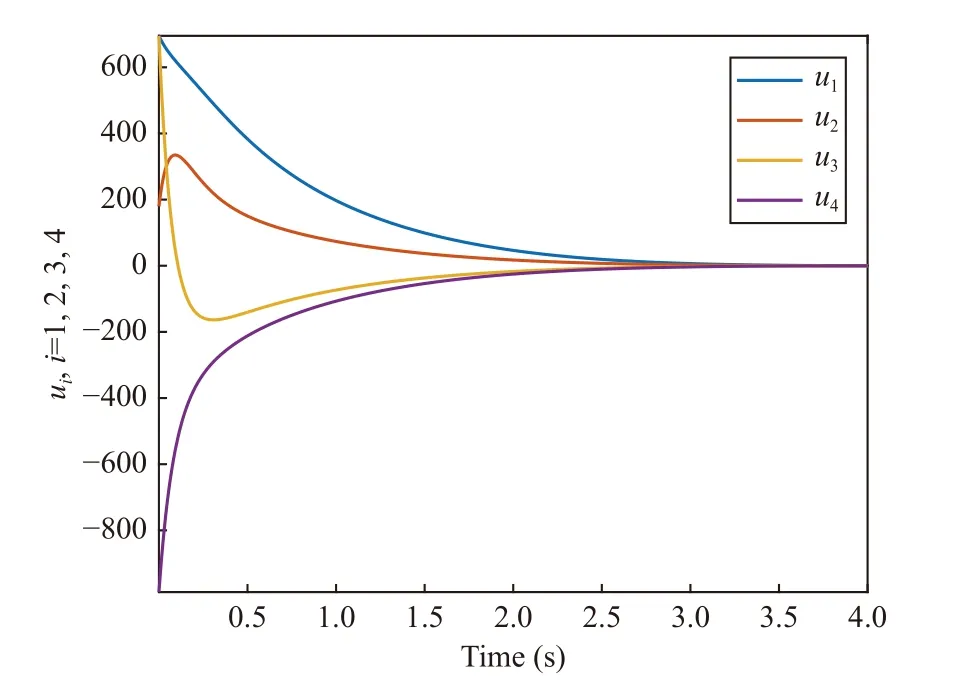
Fig. 4. State differences by using proposed controller (7).
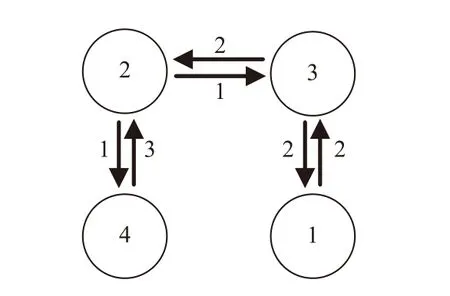
Fig. 5. Changed communication topology.

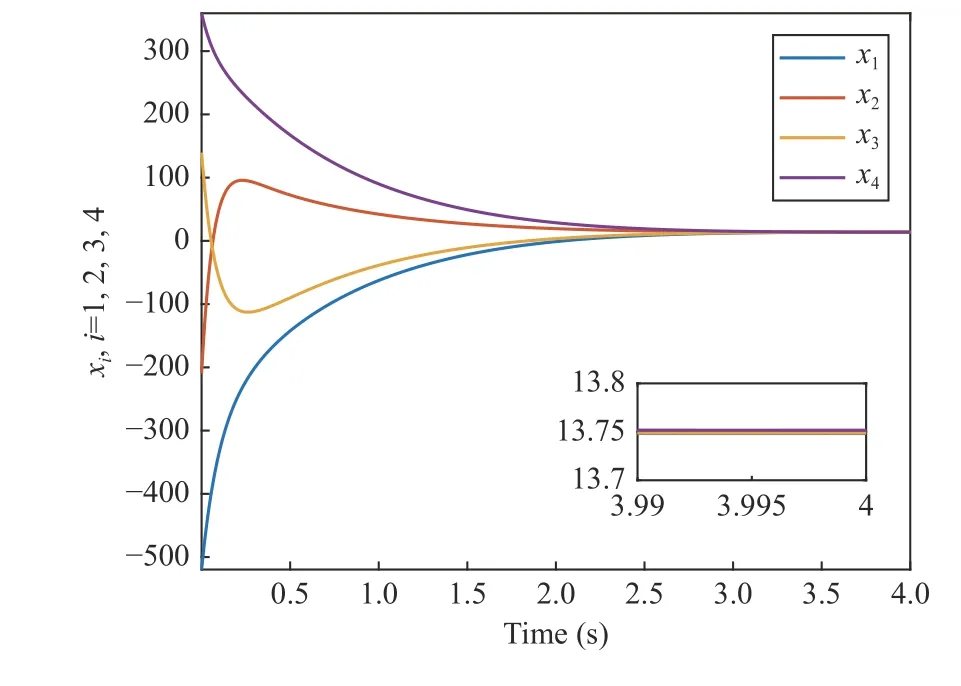
Fig. 6. Comparison to collision between agents 2 and 3.
Furthermore, under the graph in Section IV-A, we implement a controller in the form of

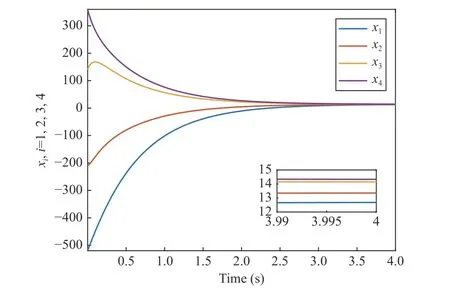
Fig. 7. Comparison to large state difference at t = 4 s.
V. CONCLUSION
This paper has investigated the order-preserved preset-time cooperative control problem of multi-agent systems. A monotone system-based approach has been proposed to guarantee the collision-free coordination. Three different distributed controllers together with sufficient conditions have been designed to realize leaderless consensus (no leaders),leader-following consensus (one leader), and containment control (two leaders), respectively. The proposed controllers contain a TBG, thus formally ensuring that the state agreement of agents is achieved in preset-time. Finally,comparison studies have been conducted through a numerical example, showing the superiority of the proposed controllers in both collision avoidance and preset-time convergence. Note that we consider single-integrator dynamics for agents in this paper. Some interesting topics such as agents with doubleintegrator dynamics and general linear dynamics deserve investigation in future work.
 IEEE/CAA Journal of Automatica Sinica2022年9期
IEEE/CAA Journal of Automatica Sinica2022年9期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Autonomous Maneuver Decisions via Transfer Learning Pigeon-Inspired Optimization for UCAVs in Dogfight Engagements
- Interval Type-2 Fuzzy Hierarchical Adaptive Cruise Following-Control for Intelligent Vehicles
- Efficient Exploration for Multi-Agent Reinforcement Learning via Transferable Successor Features
- Reinforcement Learning Behavioral Control for Nonlinear Autonomous System
- An Extended Convex Combination Approach for Quadratic L 2 Performance Analysis of Switched Uncertain Linear Systems
- Adaptive Attitude Control for a Coaxial Tilt-Rotor UAV via Immersion and Invariance Methodology
