基于CS-GRU模型的短期负荷预测方法研究*

杨海柱, 江昭阳, 李梦龙, 张 鹏

(1.河南理工大学 电气工程与自动化学院, 河南 焦作 454003；2.天津大学 电气自动化与信息工程学院,天津 300072)

0 概 述

短期负荷预测对电力系统的调度运行和市场交易都有着重要的意义，精确的负荷预测不仅帮助电力系统工作人员制定合理的生产计划，而且减少了资源浪费和用电成本[1]。

多年来，国内外学者对短期电力负荷预测方法进行大量研究，这些方法主要分三大类，第一类，基于传统数学统计模型的方法[2～4]，比如线性回归、时间序列法和指数平滑法等[2]。这些方法具有简单、计算速度快等优点，但对数据的平稳性要求较高，在处理非线性数据时预测精度较低。第二类，基于机器学习的方法[5,6]，包括人工神经网络[7]和支持向量回归机[8～10]等。以人工神经网络为代表的机器学习算法由于其预测精度高、计算能力强的优点得到了广泛关注。第三类，组合预测方法，不少专家和学者将负荷数据进行分解，采用不同的预测工具进行组合预测，提高了预测精度。文献[11]采用集合经验模态分解(ensemble empirical mode decomposition，EEMD)对电力负荷进行分解，将分解得到的高频分量利用门控循环单元(gated recurrent unit，GRU)神经网络进行训练预测，低频分量采用多元线性回归(multiple linear regression，MLR)进行预测，组合形成EEMD-GRU-MLR预测方法，不仅节省了预测时间，而且提高了预测精度。文献[12]在深度学习框架中构建长短期记忆(long short-term memory,LSTM)神经网络进行电力负荷预测。文献[13]针对负荷数据的时序性和非线性特点，考虑负荷数据内部变化规律，将输出结果与外部影响因素融合成新的输入特征，在深度神经网络下进行处理，最终提出一种基于GRU-NN模型的负荷预测方法，提高了预测速度和精度。这些方法为电力系统短期负荷预测提供了依据。

GRU不仅保留了LSTM的性能优势，而且由于调整的参数较少，大大提高了训练速度。研究发现，设定不同的超参数将影响GRU的预测效果，为了便于超参数的选择，提出一种布谷鸟搜索(cuckoo search,CS)算法和GRU相结合的预测方法。通过布谷鸟搜索算法寻优GRU的迭代次数、学习率和隐含层节点数，进一步提高GRU的预测精度。

1 GRU神经网络

循环神经网络(recurrent neural network,RNN)在处理时间序列数据时表现出优越的性能，这是因为RNN的网格中存在循环单元结构，而且允许隐藏单元之间的内部连接，使寻找非连续数据之间的时间关系成为可能[14]。但RNN存在梯度消失的问题，当时间间隔值不断增大时，RNN会失去学习过去信息的能力。为了弥补这一缺陷，专家提出LSTM神经网络，LSTM在RNN的基础上增加了三个门的逻辑控制单元：输入门、遗忘门和输出门。通过门单元的逻辑控制决定数据是否更新或是选择丢弃，克服了RNN权重影响过大、容易产生梯度消失和爆炸的缺点，现已被广泛用于时间序列数据预测当中[15,16]。

GRU是一种基于LSTM的模型的变体，它保持了LSTM性能的同时优化了LSTM的网络结构。在网络结构中，GRU网络只有更新门和重置门结构，更新门用于控制将前一时刻的信息代入当前时刻，重置门用于控制忽略前一时刻信息，相比于LSTM节省了工作内存，训练速度得到提升[17]。GRU的结构如图1所示。

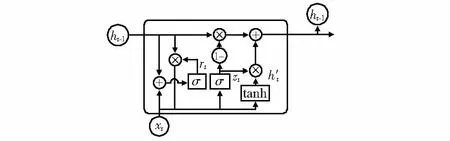
图1 GRU的网络结构

rt=σ(Wr·[ht-1,xt])

(1)

zt=σ(Wz·[ht-1,xt])

(2)

(3)

ht=(1-zt)*ht-1+zt*t

(4)

(5)

式中rt为时间t的重置门的输出，zt为时间t的更新门的输出；ht和ht-1为在时间t和t-1的输出；xt为t时刻的输入，σ为sigmoid函数，内存单元的计算过程由式(1)～式(5)计算所得。

2 CS-GRU预测模型

CS算法是杨新社教授在2009年提出的一种新兴启发算法。该算法采用莱维飞行搜索机制，具有调整参数少，易于实现，随机搜索路径优和寻优能力强等优点[18]。由于GRU的超参数对其训练速度、预测精度有一定的影响。因此，本文利用CS对GRU的超参数进行寻优，寻优的超参数包括迭代次数、学习率和两个隐含层节点数。CS优化超参数具体流程如下：

Step1 在Python的TensorFlow框架下建立CS-GRU模型。

Step2 设定鸟窝规模为Psize，最大迭代次数Miter，被宿主鸟发现的最大概率为Pa，选择测试集均方误差作为适应度函数，计算所有鸟窝适应度值。其中，每个鸟窝位置包含迭代次数、学习率和两个隐含层节点。

Step3 全局搜索。在进行全局搜索时，保存上一代质量最好的鸟窝方位，通过式(6)来调整鸟窝方位，计算鸟窝的适应度，并将上一代劣质的鸟窝方位替换

(6)

(7)

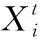
Step4 局部搜索。利用式(6)调整方位后，每个解产生一个随机数R，表示布谷鸟鸟蛋被发觉的几率，此时R与Pa=0.25比较，若RPa，此鸟窝被抛弃，产生一个新的鸟窝，具体公式如(8)

(8)

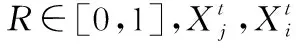
Step5 输出最优解。判定算法是否达到最大迭代终止条件或设置的误差，如果满足该条件，输出最优解，否则返回Step3继续迭代。

Step6 将优化后的超参数输入GRU进行负荷预测。

3 算例仿真

3.1 数据处理

负荷预测的精度受外界多种因素的影响，以河南省某地区90天历史负荷数据、气象数据为例进行分析，每天的数据包括最高温度、最低温度、日平均温度、相对湿度、星期类型和24个时刻点的负荷，一共29个数据特征。因各个外界因素特性和单位不同，为了预测更加精确，将这些因素进行数据归一化处理，具体操作如下:

1)负荷数据归一化

(9)

式中xnorm为归一化处理后的负荷数据，xmin和xmax为数据的最小值和最大值。

2)日期分类和归一化

采用不同的数字对应不同日期类型，周一取0.7，周二～周五取0.8，周六和周日分别取0.4，0.3。

3)温度归一化

(10)

式中Tnorm为归一化处理后的负荷数据，Tmin和Tmax为数据的最小值和最大值。

3.2 误差评价指标

采用评价指标平均绝对百分误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)计算如下

(11)

(12)

式中yi为真实值；yj为预测值；N为预测总数。

3.3 仿真分析

本文算例为河南省某地区2018年6月1日至8月29日共90天历史负荷数据，间隔时间为1 h，一共2 160个负荷数据点。以前一天的29个特征和预测当天的5个外界因素特征作为输入，预测当天24 h负荷作为输出，构建34输入24输出的预测模型。将前89天作为训练集，最后一天为测试集。为了比较GRU的预测效果与超参数设定有关，采用两组超参数进行实验，两组的批处理大小均设定为16。第一组设定GRU迭代次数为10，学习率为0.01，两个隐含层节点数为100，预测值如图2(a)所示。第二组设定GRU迭代次数为20，学习率为0.005，两个隐含层节点数为50，预测值如图2(b)所示。

图2 GRU的预测值

由图2可知，为了比较第一组和第二组预测性能，计算各组MAPE和RMSE。如表1所示，第二组相对于第一组MAPE下降了1.0 %，RMSE下降了6.93。第二组比第一组预测误差低，并且误差下降比较大，说明GRU超参数的选取对预测精度有比较大的影响。

表1 两组预测误差比较

因此，合适的超参数选取变得尤为重要，为了方便超参数的选取，利用CS对GRU的超参数进行寻优。设置鸟窝数量Psize=10，最大迭代次数Miter=10，待寻优的迭代次数、学习率和两个隐含层节点数边界依次为[100,500],[0.001,0.01],[1,200]和[1,200]。以河南省某县90天数据为例，边训练边寻优，直至CS算法达到最大迭代次数，输出最优适应度值。CS寻优超参数过程如图3所示。

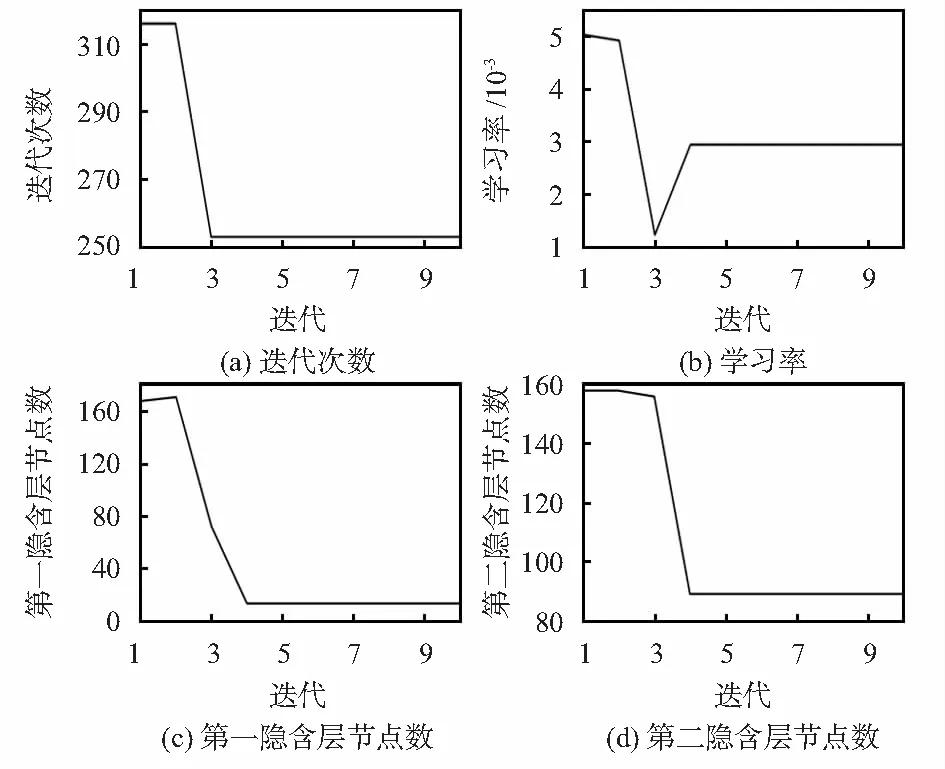
图3 CS寻优超参数过程

CS寻优迭代结束后，输出迭代次数为253，学习率为0.002 948，第一隐含层节点数为13，第二隐含层节点数为89，将这些超参数输入到GRU，得到的预测结果如图4所示。

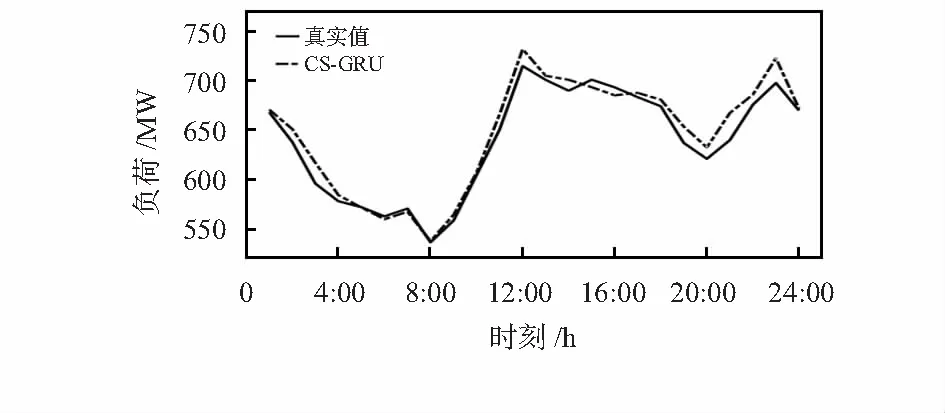
图4 CS-GRU预测值

为了更好地展现CS-GRU模型的预测能力，将CS-GRU模型与各模型比较，如图5所示。

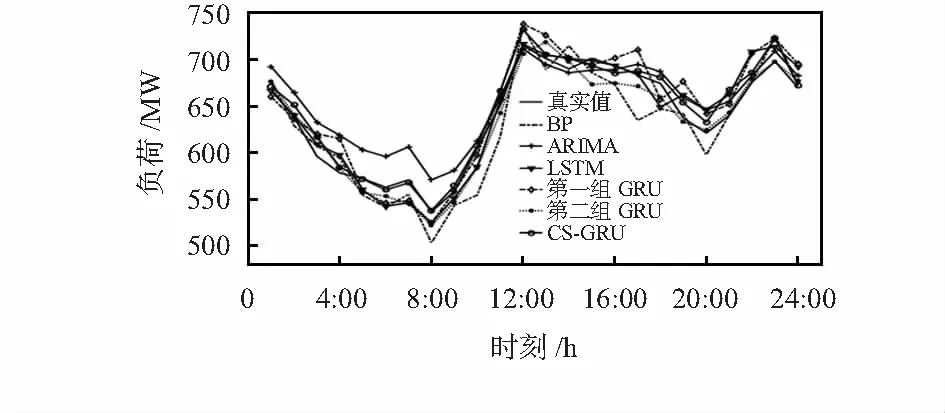
图5 CS-GRU预测值与各个模型比较

从表2可知，CS-GRU模型的MAPE和RMSE比第一组的GRU分别下降了1.4 %和8.69，比第二组的GRU分别下降了0.4 %和1.76。说明经过CS寻优后的GRU预测精度有所提高。对比BP，ARIMA和LSTM预测模型，CS-GRU预测效果最好。

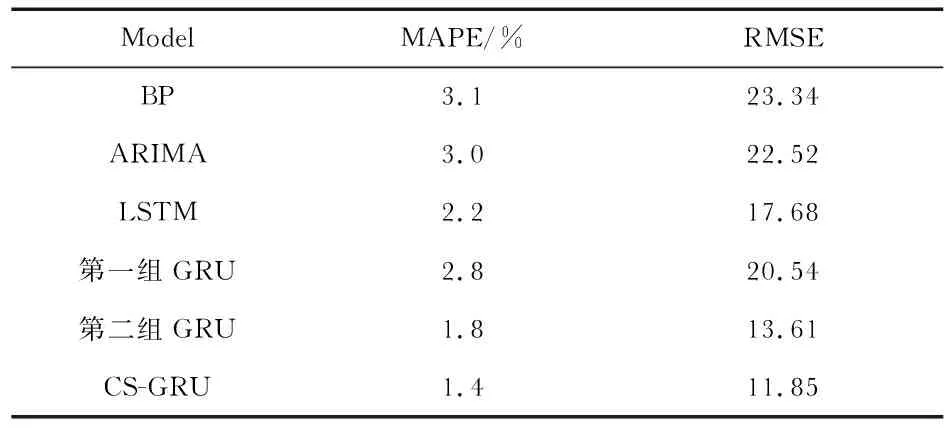
表2 各模型预测误差对比

4 结束语

为了方便超参数的选取，本文提出一种CS算法和GRU神经网络相结合的预测方法。通过CS算法寻优GRU的迭代次数、学习率和两个隐含层节点数，提高了GRU的预测精度。通过河南某地区算例，将CS-GRU模型与BP、ARIMA、GRU、LSTM模型进行对比。结果表明，CS-GRU的预测效果最好。