连续配筋混凝土复合式沥青路面层间接触对其力学响应影响研究

邓凤祥 秦 苗 李 盛 梁晓东

(湖南省交通科学研究院有限公司1) 长沙 410015) (长沙理工大学交通运输工程学院2) 长沙 410114) (湖南联智科技股份有限公司3) 长沙 410019)

0 引 言

公路及城市道路沥青路面的车辙变形已成为主要的早期病害类型，主要原因有两个方面：①高温和重载作用下，沥青路面的车辙变形必然会较大，尤其是在长大纵坡及车辆起动和制动较频繁的路段；②部分沥青结合料高温稳定性较差或沥青混合料材料组成设计不合理，导致沥青混合料在行车荷载和温度综合作用下易发生侧向剪切流动[1-5].对于连续配筋混凝土复合式沥青路面(CRC+AC复合式路面)，施工时沥青混凝土如果直接摊铺在连续配筋水泥混凝土板上，由于AC层和CRC板之间不同于沥青面层内部存在集料的嵌挤作用，仅靠沥青混合料内聚力以及沥青层与配筋混凝土板间的接触摩擦来抵抗水平剪力，抗剪能力相对其他路面结构较弱[6-8].且由于CRC+AC复合式路面结构特殊和相对复杂，其力学响应受层间接触的影响更为显著.Das等[9]研究发现黏层类型对刚柔复合式路面结构最大剪切强度影响显著.Kruntcheva等[10]通过研究层间接触与路面结构层间界面抗剪切强度之间的关系，得出层间连续或良好的接触能提高路面结构的层间抗剪强度.彭妙娟等[11-12]指出良好的层间接触可以有效提高路面抗车辙能力.任少博等[13]研究发现，对于复合式路面界面构造深度较好时，路面整体抗变形能力明显提高.纪小平等[14]研究表明：黏层可有效提高层间抗剪强度，从而提高复合式路面高温性能.李盛等[15]分析了三向非均布应力下CRC+AC复合式路面力学响应，但未充分考虑层间接触对力学响应的影响.

我国沥青路面结构设计的基本理论为弹性层状体系理论[16]，计算时层间接触状态假设为完全连续，与实际路面结构的层间接触状态不一致，特别是用做层间接触处理的粘层材料类型及用量都会影响层间的接触水平，如果层间接触不佳将导致层间界面成为整个路面结构的薄弱环节，路面结构的力学响应也将发生变化，最终加速路面结构服役寿命衰减.文中利用Abqaqus建立沥青混合料蠕变模型和弹性模型，模拟连续变温条件下在不同轴载及层间接触条件下的刚柔复合式路面车辙变形，以及不同层间接触对沥青面层的力学响应，提升夏季高温条件下刚柔复合式路面抗车辙病害及结构设计水平.

1 CRC+AC复合式路面有限元模型建立

1.1 路面模型建立

沥青面层为分上、下两层的黏弹性材料，其中上面层4 cm的AC-13，下面层为8 cm的AC-25，CRC板厚度24 cm、基层和粒料层分别为36 cm的水泥稳定碎石、15 cm的级配碎石.路面结构形式见图1.

图1 路面结构示意图

运用ABAQUS建立三维模型，考虑到荷载和结构的对称性，可采用1/2模型，模型尺寸：路面宽度(X轴方向)为2 m，路面深度(Y轴方向)为3 m，行车方向(Z轴)长度为3.5 m.采用非均匀网格，面层网格划分更精细，面层以下区域划分粗糙，见图2.

图2 模型网格划分图示

在温度场计算时单元类型采用DC3D8，其他计算采用C3D8R的单元类型，左右两侧水平方向约束，模型底部为竖向约束[17].

1.2 路面结构计算参数确定

结合文献[17]和实体工程情况，确定CRC板与基层及土基的参数，见表1.沥青层考虑材料的粘弹性，参数取值见表2.

表1 CRC板、基层和土基材料特性

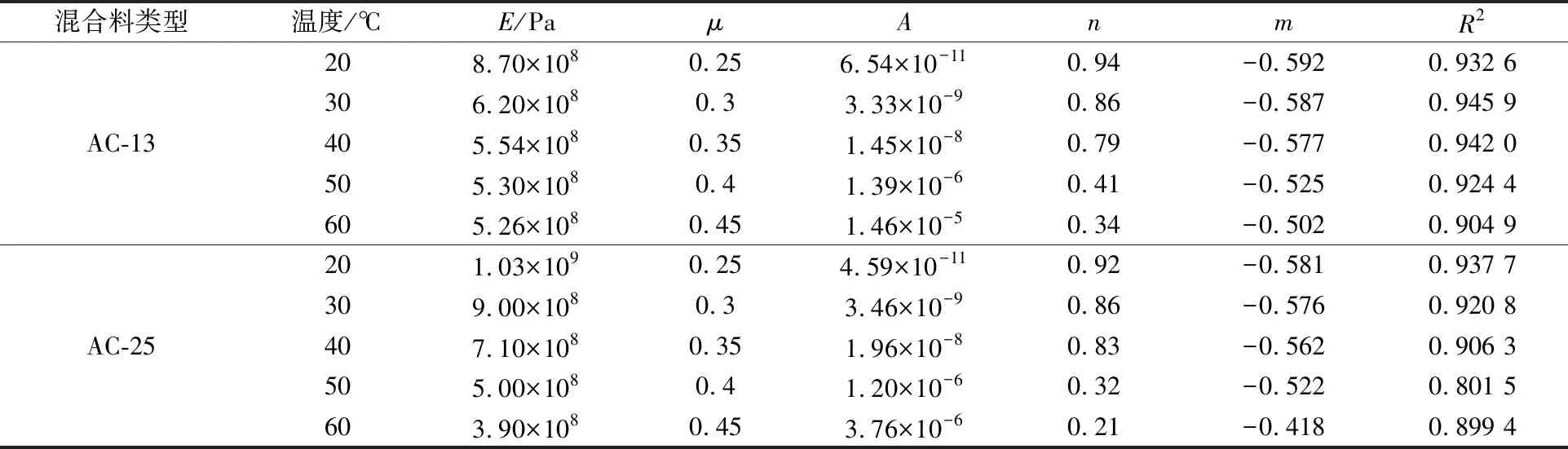
表2 沥青层弹性参数和蠕变参数

1.3 荷载模型的建立

采用单轴双轮的BZZ-100竖向均布荷载，每个轮胎的胎面可以等效为0.192 m×0.186 m的矩形，轮胎接地压强为0.7 MPa，双轮间距为0.32 m，单侧双轮中心距路面中线0.91 m[18]，见图3.

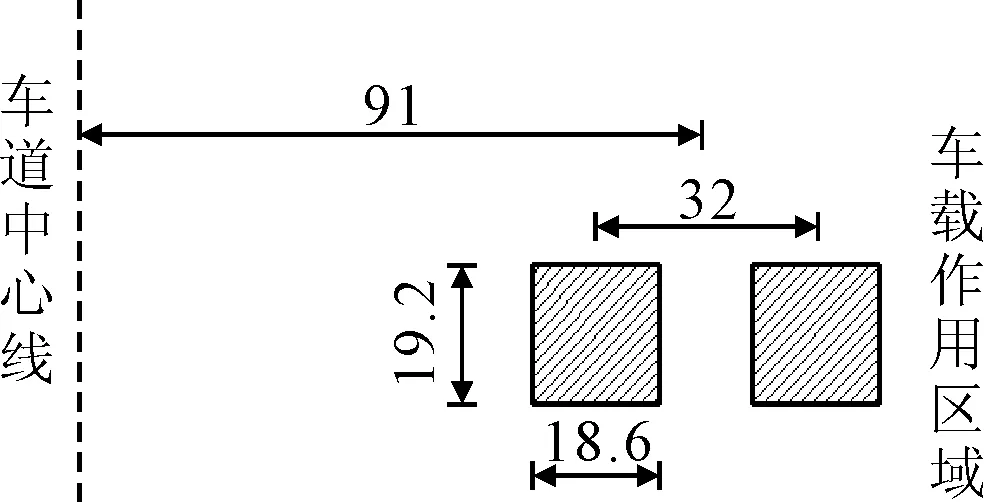
图3 荷载示意图

考虑面应力影响，面应力的大小为竖向均布荷载与水平力系数的乘积，作用区域同竖向均布荷载.参考文献[18]，当车辆在紧急制动等不利状态行驶时，选取水平力系数为0.5.

1.4 层间接触条件设置

建模时通过Abaqus软件中的Interaction模块可以设置不同的层间接触条件，路面结构层间接触状态用摩阻系数f来表征.

主要考虑路面结构在沥青面层和CRC板之间的粘结情况对面层的车辙影响，因此只设置一个接触面，沥青层底面作为接触对的主面，CRC板表面作为接触对的从面.

2 CRC+AC复合式路面结构温度场研究

2.1 温度场相关理论

1) 太阳辐射模拟 太阳辐射热交换的日变化过程可采用函数近似表示.

(1)

式中：q0为太阳日最大辐射，q0=0.131Qm,Q为太阳日辐射总量，J/m2；m=12/c;ω为角频率，ω=2π/24，rad；c为实际有效日照时数，h.

在ABAQUS有限元软件中通过Load模块以及子程序DFLUX，实现太阳辐射的数值模拟.

2) 气温及对流热交换 气温变化过程可通过正弦函数线性组合式模拟.气温与对流交换通过ABAQUS有限元软件中的Interaction模块与子程序FILM来模拟.

0.14sin(2ω(t-t0))]

(2)

3) 路面有效辐射 路面有效辐射可采用式(3)表征，通过ABAQUS有限元软件中的Interaction模块进行定义.

qF=εσ[(θ1|Z=0-θZ)4-(θa-θz)4]

(3)

式中：qF为地面有效辐射，W/(m2·℃)；ε为路面发射率，取0.81；σ为Stefan-Boltzmann常数，σ=5.669 7×10-8,W/(m2K4)；θ1|Z=0为路表温度，℃；θa为大气温度，℃；θz为赴力学零度值，℃，θz=-273 ℃.

2.2 温度场分析

通过有限元三维模型进行传热计算，可得到夏季高温季节1d24 h内CRC+AC复合式路面各结构层的温度变化情况.以路面结构沿行车方向的横断面为分析对象，提取24 h内不同时刻和不同深度处的温度值，得到CRC+AC复合式路面结构的温度场数据，见图4.

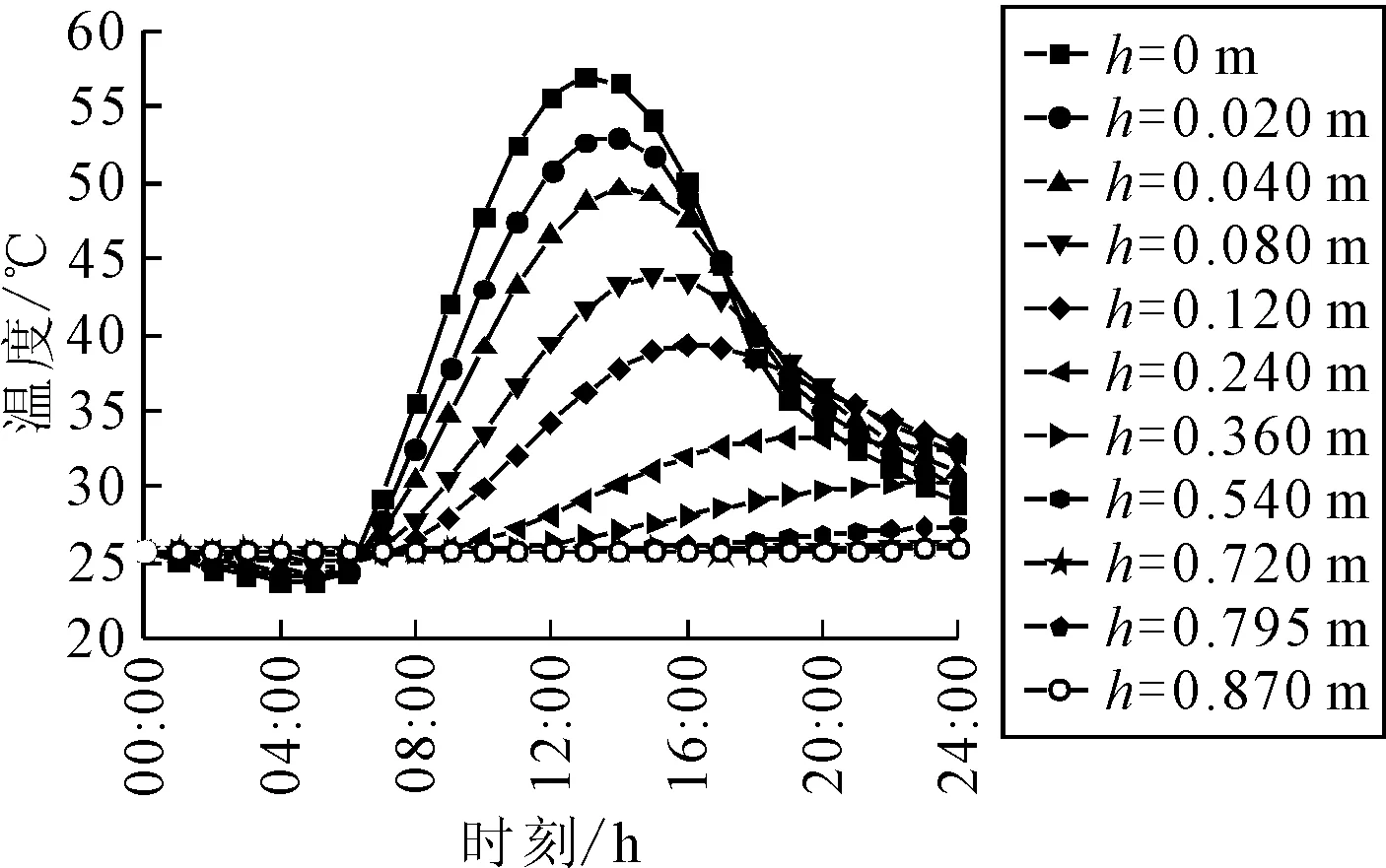
图4 温度随深度和时间变化情况

由图4可知：路面各结构层温度受大气温度及太阳辐射影响，热量由面层结构逐渐向下部结构传递.面层结构直接经受外部环境的作用，加之沥青混合料对温度的敏感性较高，因而面层结构的温度及其变化幅度是最大的.面层结构温度在上午06:00—12:00急剧升高，在13:00达到峰值58 ℃，此时路面面层大部分结构处于高温工作状态.随后在14:00至日落前后面层温度开始显著下降.而面层以下的CRC板温度增长相对比较平缓，在18:00左右达到峰值，约为35 ℃.基层温度缓慢变化，变化幅度并不大，直至24:00最高温度仍维持在27 ℃.对于CRC+AC复合式路面，面层以下的温度相对比较稳定.由此可见，路面面层结构对环境温度及太阳辐射较为敏感，面层温度会随着气温及日照的强度呈现较大幅度的变化.

3 层间接触对车辙及力学响应的影响分析

3.1 层间接触对车辙的影响分析

影响路面车辙的主要原因包括汽车荷载的频繁加载和卸载，蠕变模型分析中不仅要考虑材料参数，还要考虑荷载作用时间.通过将路面结构所承受的多次荷载等效为汽车荷载累计作用时长，实现汽车荷载多次作用的模拟.荷载累计作用时间为

(4)

式中：t为轮载累计作用时间，s；N为轮载作用次数，次；P为车辆轴重，100 kN；nw为轴的轮数，四个；p为轮胎接地压力，700 MPa；B为轮胎接地宽度，21.3 cm；V为行车速度，80 km/h.

表3为不同轴载作用次数对应的累计作用时间.

表3 不同轴载作用次数对应的累计作用时间

沥青面层与CRC板的层间接触状态用可用摩擦系数f来表示，取值为0～1之间，当f=1时，为完全连续的层间接触状态，当f=0时，为完全光滑的层间接触状态.目前实体工程中一般会对沥青面层与CRC板的层间用同步碎石封层进行处理，所以文章研究层间接触状态对沥青面层车辙深度的影响，不考虑完全光滑的层间接触状态，f值分别取0.1，0.3，0.5，0.7，1.0.不同层间接触情况和轴载作用次数对车辙深度的影响见图5.

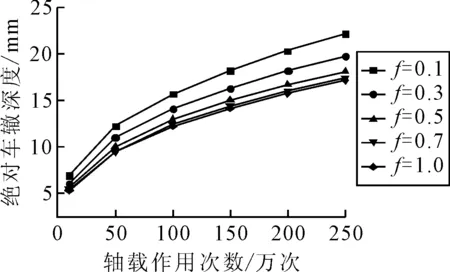
图5 车辙深度与轴载作用次数及层间接触的关系

由图5可知：随轴载作用次数增加，车辙变形逐渐增大，且增量逐渐减少最后趋于稳定.沥青面层和CRC板之间的层间接触由完全连续到不完全连续时，随层间摩阻系数减小，车辙变形不断增大.以轴载作用次数250万次为例，f=0.7的车辙深度相对连续的增量为1.8%，f=0.5相对增量为5.6%，f=0.3相对增量为15.5%，f=0.7相对增量为29.4%.改善复合式路面沥青面层与CRC板的层间接触可有效减少车辙.

3.2 层间接触对力学响应分析

CRC+AC复合式路面沥青面层车辙破坏与面层内部应力大小和分布情况密切相关.计算不同接触状态下的力学指标时，根据计算结果和路面的受力特点，轮迹中心的竖向应力较大，轮迹后端的纵向应力较大，轮隙处有较大的横向应力，荷载边缘的剪应力较大.因此计算竖向应力选轮迹中心为计算点位，计算纵向应力选轮迹后端为计算点位，计算剪应力时取轮迹外侧边缘为计算点位，以轴载作用次数为250万次为例.结果见图6.

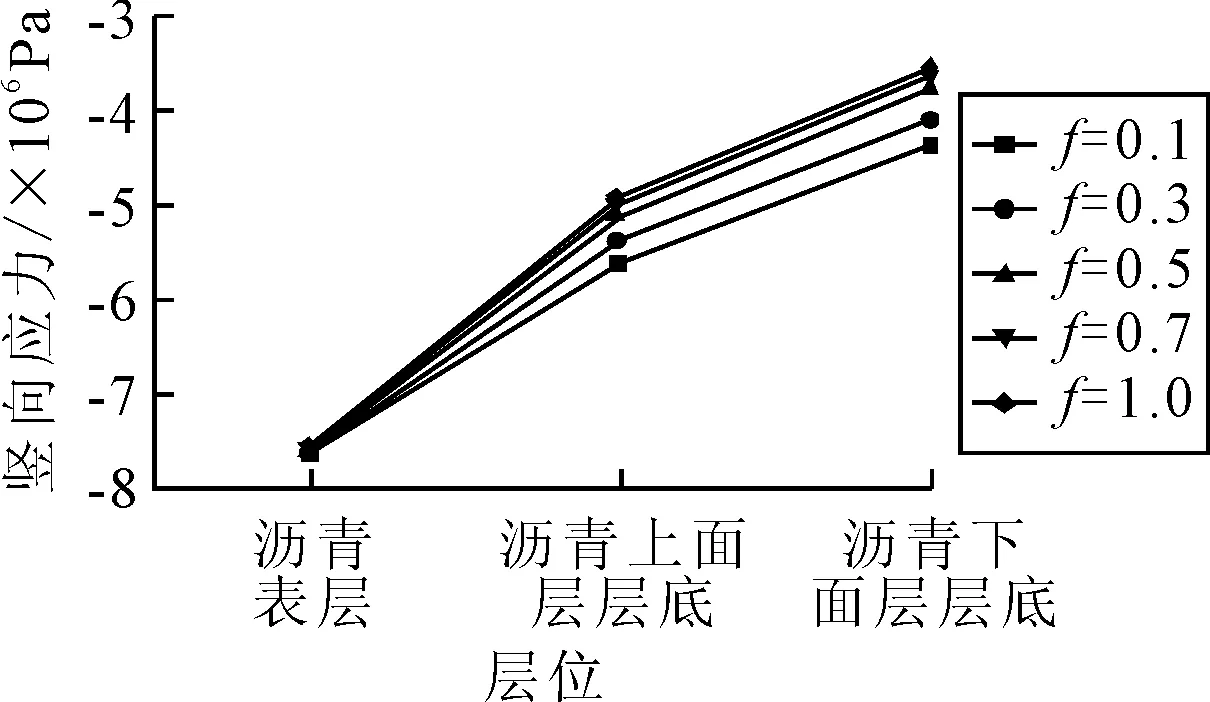
图6 不同沥青层层位的竖向应力

由图6可知：在行车荷载作用下，CRC+AC复合式路面结构内的压应力由沥青层表面逐步向下扩散传递，到基层底部压应力峰值变得较小.路表压应力在不同层间接触条件下应力峰值相差不大，而上面层底压应力在f=0.1条件下相较于f=1时增长了14.15%，下面层底压应力在f=0.1条件下相较于f=1时增长了23.23%.沥青面层与CRC板的层间接触条件对靠近CRC板的面层压应力影响更大.

计算纵向应力(σz)在深度方向的分布、横向应力(σx)在深度方向的分布，分析层间接触对沥青面层内部力学响应的影响规律，结果见图7.

图7 纵、横向应力沿路表深度分布

由图7可知：沥青面层与CRC板之间的层间无论是完全连续还是摩擦接触时，纵向拉应力与横向拉应力沿深度的变化规律大体一致.沥青表面层纵向拉应力在沥青面层与CRC板层间不连续与完全连续时相比最大应力增加了30.4%，沥青下面层底层纵向拉应力在沥青面层与CRC板层间不连续与完全连续时相比最大应力减小了31.6%，AC层与CRC板层间的不连续引起的最大纵向拉应力变化较为明显.不同的层间接触条件下，对AC层的表面层横向拉应力影响更大，沥青表面层横向拉应力在沥青面层与CRC板层间不连续与完全连续时相比最大应力增大了31.0%，在距路表0.08 m以下的面层横向拉应力大小接近一致.因此,不同的AC层与CRC板层间接触状态对于沿路表深度纵向拉应力分布影响较大，而对于横向拉应力的影响主要集中靠近表面层.

横向剪应力是导致路面产生车辙病害的主要原因.计算不同层间接触状态下横向剪应力(τyz)在深度方向上的分布，结果见图8.

图8 横向剪应力沿路表深度分布

由图8可知：对于CRC+AC复合式路面，层间接触状态对界面层可能出现的横向剪应力峰值(τyz max)有较大影响.在面层连续的情况下，上面层深度范围内，横向剪应力在路表下1～4 cm处出现峰值.当接触系数f=0.1时，沥青面层和CRC板的界面层可能出现的横向剪应力峰值只有0.045 MPa，是完全接触时的25%；当接触系数f=0.7时，沥青面层和CRC板的界面的横向剪应力峰值为0.188 MPa，为层间完全接触时的98%；层间接触越好，层间界面的横向剪应力峰值越大，说明层间接触良好可更好地传递行车荷载的水平力作用，有利于减小沥青面层的剪切开裂.

4 结 论

1) 随轴载作用次数增加，车辙变形逐渐增大，且增量逐渐减少最后趋于稳定；随层间摩阻系数减小，车辙变形不断增大，即层间接触差则车辙变形更大.

2) 沥青面层的压应力随着摩擦系数的增大而减小，且沥青面层与CRC板的层间接触状况对靠近CRC板的下面层压应力影响更大，沥青面层的层间接触状态越好，越不容易产生压密型车辙.

3) 沥青面层与CRC板之间的层间无论是完全连续还是摩擦接触时，纵向拉应力、横向拉应力沿深度的变化规律大致相同；不同的接触状态，对于沿路表深度纵向拉应力分布影响较大，而对于横向拉应力的影响主要集中靠近表面层.

4) 当接触系数f=0.1时，界面层τyz max=0.045 MPa是完全接触时的25%；当接触系数f=0.7时，界面层τyz max=0.188 MPa是完全接触时的98%，良好的层间接触可以更好地传递车辆荷载的水平作用力，有利于减小沥青面层的剪切开裂.