基于无模型自适应控制的底栖式AUV 路径点跟踪控制
高 鹏,万 磊,徐钰斐,陈国防,张子洋
(哈尔滨工程大学 船舶学院水下机器人技术重点实验室,黑龙江 哈尔滨,150001)
0 引言
海洋石油是地球上最丰富的自然资源之一。全球石油总储量的34%都蕴藏在海底,目前的开采技术尚处于勘探早期阶段,海洋石油资源开发已从水深300 m 扩展至水深3 000 m 的深海区,与之相应的海洋石油勘探也逐渐向深海发展。当前主要的海底石油勘探设备采用海底节点(ocean bottom node,OBN)技术[1-3],将地震检波传感器集群布放到海底,可独立采集、记录信号。然而,大部分OBN 产品不具备运动能力,因此布放回收效率较低,影响了海底地震数据的精确采集,难以满足地震勘测应用的大规模组网布放需要。
在此背景下,一种搭载地震检波装置的底栖式AUV 的概念被提出[4-6],它是一种将地震检波技术应用于自主水下航行器(antonomous undersea vehicle,AUV)的新型海洋石油勘测装备,其布放回收过程如图1 所示。该设备在运动到海底目标位置后可以长期坐底采集海底地震数据,作业完成后上浮至指定海域,由母船进行统一打捞回收。在自水面布放到实现坐底探测的过程中,各底栖式AUV 会按照既定的航线运动,从而避免相互之间的碰撞和干扰,因此对底栖式AUV 进行指定路径点下的精确路径跟踪控制显得尤为重要。

图1 单个底栖式AUV 布放回收过程Fig.1 Layout and recovery process of single benthic AUV
底栖式AUV 在路径跟踪过程中,出于能源节约角度的考虑,通常会关闭横向推进器,仅在2 个水平推进器的作用下实现路径点跟踪控制,因此其是一种欠驱动控制系统。欠驱动路径点跟踪控制通常被分为制导子系统和航向子系统。制导子系统中,视线制导(line of sight,LOS)方法因其制导效率高、使用便捷等特性被广泛应用。而在航向子系统中,一些典型的先进控制方法能确保AUV 在一定时间内实现航向控制,并保持在期望的运动路径上。
近年来,已有不少学者研究了AUV 的路径点跟踪控制问题。Abdurahman 等[7]提出了一种封闭型LOS 制导律下的切换型制导算法,解决了跨轨误差较大时传统封闭型制导律与当前路径可能没有交点的问题,实现了AUV 的路径点跟踪控制。Huang 等[8]设计了一种凸映射下的路径点跟踪控制器,该方法可以较好地提高路径跟踪的收敛性能,并减小实际航向角与期望航向角之间的误差。Elmokadem 等[9]设计了一种基于滑模变结构控制的AUV 路径点跟踪控制器,解决了在模型存在不确定性以及未知洋流干扰下的鲁棒控制问题。
然而,上述方法大多是建立在精确模型的基础上,而AUV 模型具有较高的不确定性和参数摄动性,因此基于模型的控制方法工程实用性较差。
无模型自适应控制方法(model-free adaptive control,MFAC)是Hou 等[10]于20 世纪90 年代提出的一种数据驱动控制方法。其控制器设计仅仅依赖被控对象的输入/输出测量数据,不需要被控对象的结构或动力学信息,因此不存在建模过程、未建模动态和关于对象动态的理论假设。此外,MFAC 控制器的参数会根据实时的输入/输出数据变化在线调整,因此该控制方法具有良好的自适应能力。由于上述优点,该方法已经在高速电机控制[11]、电力系统[12]、图像处理[13]、自动汽车控制[14-15]、四旋翼飞行器控制[16]以及工业控制[17]领域得到了广泛的应用。
基于此,文中将MFAC 方法应用于AUV 路径跟踪子系统,研究了底栖式AUV 的路径点跟踪控制问题。文章的主要贡献包括:
1) 将MFAC 方法应用到了AUV的航向控制子系统,该方法采用的控制器设计与控制对象模型参数无关,可以实现不确定条件下的自适应控制;
2) 设计了一种改进型MFAC 航向控制器,该算法可以有效解决传统MFAC 控制算法应用于航向控制时由于积累效应可能导致的超调大、收敛速度较慢等问题;
3) 提出了一种双曲正切型变航速制导策略,该策略可以使AUV 在路径点切换处具有较小的偏航距离与航向改变,可实现转弯时的平滑过渡,提高路径跟踪控制的精度。
1 AUV 模型建立及控制问题描述
1.1 运动学及动力学模型介绍
由于垂直面有独立的推进器进行控制,因此忽略系统耦合的影响,重点研究底栖式AUV 的水平面路径跟踪控制问题。
图2 所示为底栖式AUV 外形结构图。有别于常规的鱼雷状AUV,底栖式AUV 是一种半开架式结构。此外,AUV 配有多方向的推进器,控制输出范围较广,可以实现原地转弯,因此可以较好地实现底栖。

图2 底栖式AUV 外形结构图Fig.2 Outline structure of a benthic AUV
AUV 水平面运动学方程可表示为

式中:η=[x,y,φ]T为大地坐标系下AUV 的位置与航向角;υ=[u,v,r]T为随体坐标系下AUV 的纵向、横向速度以及角速度;R(φ)∈R3×3为旋转矩阵,具体表达式为

将式(1)展开可得
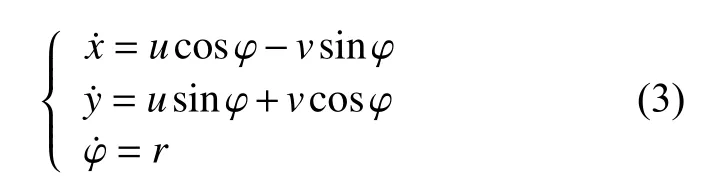
AUV 动力学方程可表示为
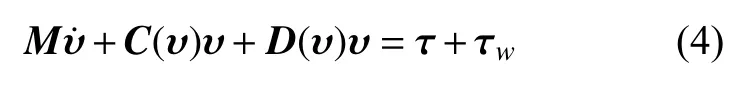
M∈R3×3,C(υ)∈R3×3,D(υ)∈R3×3
式中,分别为惯性矩阵、科里奥利矩阵以及流体阻尼矩阵,具体表达形式为

向量τ=[τu,0,τr]表示纵向推力与转向力矩,代表AUV 的控制输入,τw=[τwu,τwv,τwr]表示系统的外界环境干扰。
根据式(5),将式(4)展开可得底栖式AUV 动力学方程为

式中,mij和di j(i,j=1,2,3)分别为AUV 的惯性质量系数与水动力系数。
1.2 路径点跟踪控制问题描述
底栖式AUV 路径点跟踪控制如图3 所示。XEOEYE和XBOBYB分别表示大地坐标系和随体坐标系;pn(xn,yn),(n=1,2,3···)为指定的跟踪路径点;(xt,yt)为AUV 在大地坐标系下的实时坐标;φ为AUV 的当前航向角;φd为制导律下的目标航向角;φp为AUV 当前跟踪路径的路径角;u和v分别表示AUV在随体坐标系下的纵向与横向速度;βφ=atan(v/u)为AUV的侧滑角;为AUV的总合成速度;ye为交叉跟踪误差,表示AUV距离当前航线的垂向距离,由坐标转换关系,其在大地坐标系下的计算公式为

图3 底栖式AUV 路径点跟踪控制示意图Fig.3 Schematic diagram of waypoint-tracking control of a benthic AUV

底栖式AUV 的路径点跟踪控制问题表述如下:假设点pn(xn,yn),(n=1,2,3···)为一系列指定的路径点,AUV 需要在2 个水平推进器的作用下设计相关的航速与航向控制律,使AUV 能够在一定时间内以恒定的纵向速度跟踪制导律下的目标航向 φd,从而跟踪由路径点组成的直线路径,并保证跟踪误差ye在一定时间内收敛到0。在AUV距离当前路径点的距离小于切换半径Rt时,默认当前路径点跟踪完成,切换为下一路径点,进行下一组路径点的跟踪,直至完成全部路径点的跟踪任务。
根据上文描述,传统的AUV 路径点跟踪控制问题可用数学形式表达为

AUV 路径点跟踪控制框图如图4 所示。
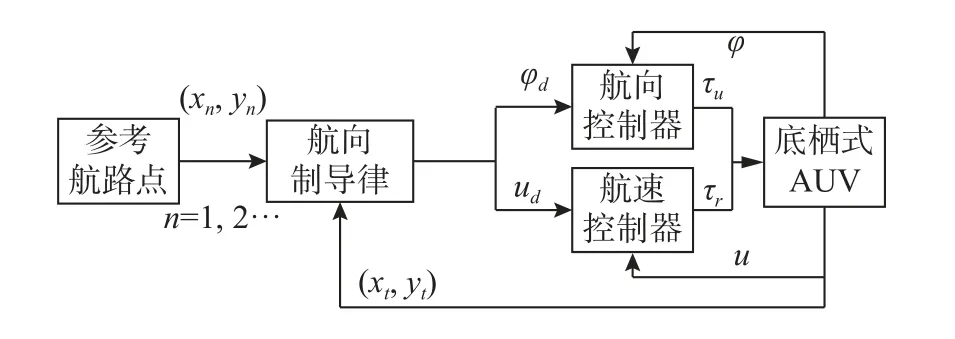
图4 底栖式AUV 路径点跟踪控制系统框图Fig.4 Block diagram of a benthic AUV waypoint-tracking control system
2 路径点跟踪控制器设计
2.1 MFAC 方法介绍
MFAC 方法的基本思想是:在闭环系统的每个动态工作点处建立一个等价的动态线性化数据模型,然后基于此等价的虚拟数据模型设计控制器并进行控制系统的理论性分析,进而实现非线性系统的自适应控制[10],其控制流程如图5 所示。其中,动态线性化模型的参数仅通过被控对象的输入/输出数据进行在线估计,并不需要任何关于系统模型的先验知识。动态线性化方法有3 种具体形式,分别为紧格式动态线性化(compact form dynamic linearization,CFDL)、偏格式动态线性化(partical form dynamic linearization,PFDL)以及全格式动态线性化(full form dynamic linearization,FFDL)[18]。其中,CFDL 方法对于一般的离散时间非线性系统而言,其线性化效果较好,故文中基于该方法进行了航向控制器的设计。
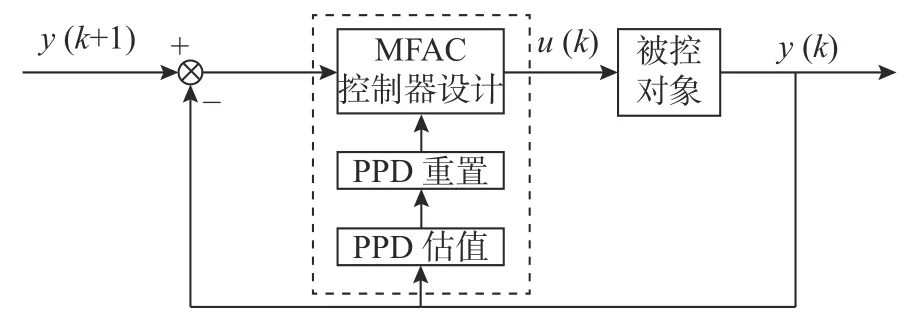
图5 无模型自适应控制框图Fig.5 Block diagram of MFAC
对于一般的离散时间非线性系统,可以表示为

式中:u(k)和y(k)表示系统在k时刻的输入和输出;ny、nu表示系统的输出与输入的阶数。
现提出如下假设。
假设1:函数f关于各个变量都存在连续的偏导数。
假设2:系统满足广义Lipschitz 条件,即对于任意k1≠k2,k1、k2>0,有

式中,b表示大于0 的常数。
引理1[18]:对于满足假设1 与2 的离散系统,当∆u(k)≠0时,一定存在一个时变参数φc(k),使系统可以转化为CFDL 模型,即
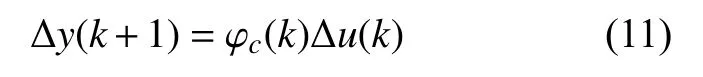
式中,∆为当前时刻与上一时刻的状态量差值。此外,对任意时刻k,φc(k)都是有界的。
2.2 无模型自适应航向控制器设计
2.2.1 传统的无模型自适应航向控制算法
假设3:对于某一给定的期望输出信号y(k),总存在一个有界的输入u(k),使系统在此控制输入信号的驱动下其输出等于y(k)。
假设4:对任意时刻k以及∆u(k)≠0时,系统的伪偏导数符号保持不变,即满足:φc(k)>δ或φc(k)<−δ,其中 δ为很小的正数。文中假设伪偏导数符号始终为正。
由于伪偏导数φc(k)是有界的时变未知量,需要对其进行在线估计,其估计算法为
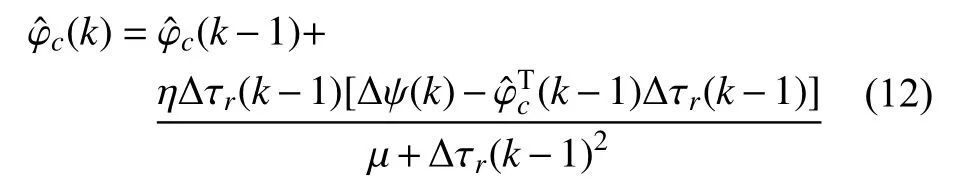
接着,考虑如下控制输入准则函数

式中:φd(k) 与φ(k)为系统在k时刻的期望航向与实际航向;λ为权重因子,用来限制控制输入的变化。将式(13)对τr(k)求偏导后令其为0,并代入式(12),可以得到如下MAFC 算法
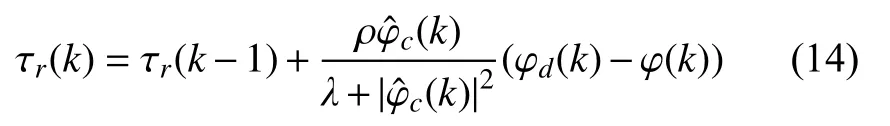
式中,伪偏导数的估计算法为

式中:sgn表示符号函数;ε为一个很小的正数。上式中加入的伪偏导数重置机制可以保证伪偏导数算法具有对时变导数更强的跟踪能力,从而增加系统的稳定性。
引理2[19]:对于满足假设1~假设4 的非线性系统,当期望输出φd(k+1)=φd(k)=const时,使用式(15)所表示的伪偏导数估计算法,可以保证伪偏导数估计误差有界。
2.2.2 改进的MAFC 算法
式(14)所表示的无模型自适应控制器具有积累效应,即当前时刻的控制输出是根据之前时刻的输出累加而成。当初始航向误差较大时,控制器的输出值会慢慢累加到一个较大值,因此收敛速度较慢。另外,由于输出的积累效应影响,当实际航向超过期望航向时,AUV 的航向会出现超调,从而影响系统的控制精度。
为了解决这一问题,文中提出了一种改进的无模型自适应航向控制算法(improved modelfree adaptive control,IMFAC)。IMFAC 算法的表达式为

式中,φd∗(k)为系统在k时刻新的期望输出值,其表达式为

式中:φd(k)为系统在k时刻的原期望航向;α 为正常数;φ0为单位节拍AUV 在最大转向力矩驱动下的转向角,可以通过试验测出。从式(17)中可以看出,当初始航向误差较大时,AUV 的期望输出会在原来的基础上有一定的增幅,从而能够加快航向的收敛。另一边,由于收敛速度较快,航向的历史积累值减少,系统在期望航向处的超调较少,控制精度也得到了改善。IMFAC 航向控制流程如图6 所示。

图6 IMFAC 航向控制框图Fig.6 Block diagram of IMFAC course control
定理1:针对系统(9),在满足假设1~假设4 的前提下,采用式(15)、式(16)和式(17)表示的IMFAC航向控制器,则存在一个正数λmin,使得当λ>λmin时,有
2) 闭环系统是BIBO 稳定的,即系统的航向输出φ(k)和输入τr(k)是有界的;
证明:首先证明期望航向为定值且大于0 时的情况,即

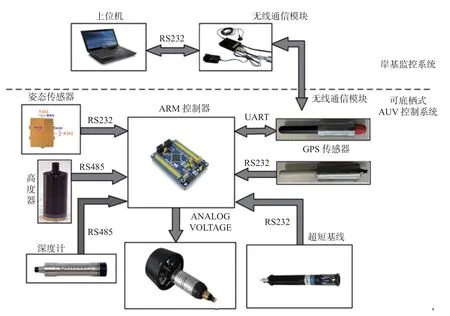
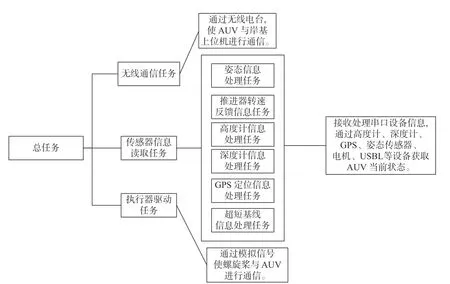
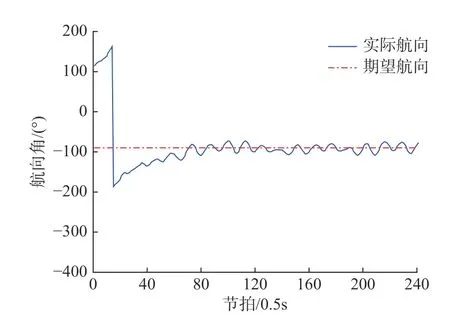
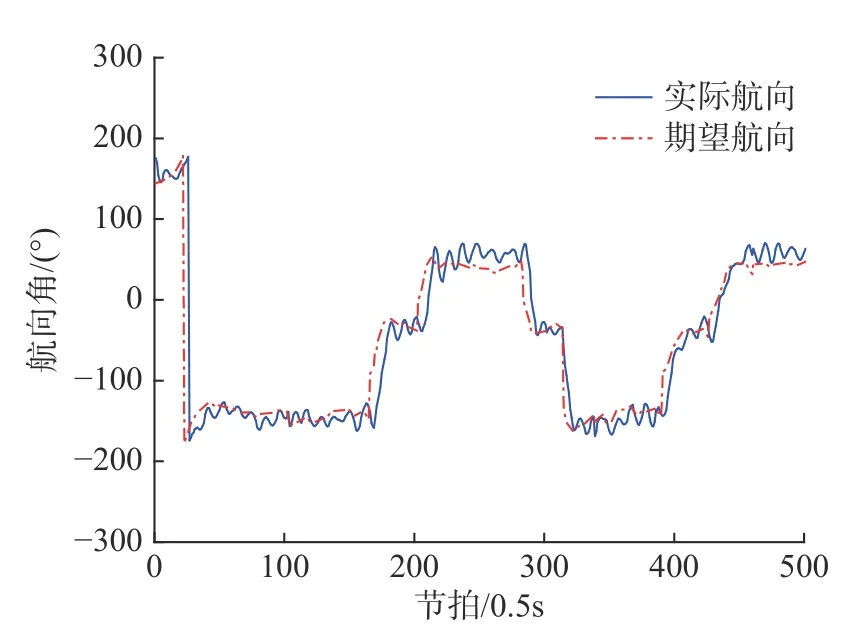
由于f(k)随着航向误差的减小而减小,因此f(k+1) 由引理1 可知,φc(k)是时变正常数且有界,而由引理2 可知,有界。因此,设 |φc(k)|≤b,当λ>λmin=b2/4时,有 因此,有 将式(24)代入式(22),得 由式(25)可以得出,当k足够大时,e∗(k+1)收敛。而当航向误差较小时,f(k+1)近似为0,因此,有 同理可证得期望航向小于0 时航向误差的收敛,因此定理1 中的结论1)成立。由于 φd为常数,则跟踪误差e∗(k+1)的收敛意味着航向角φ(k)的有界。 由式(25)和式(27)可知 因此,系统输出τr(k)有界,定理1 中的结论2)成立。 当期望航向为非定值时,建立增广系统 针对此增广矩阵应用MFAC 方案,即可证明增广系统(29)的稳定性和单调收敛性。由于增广系统的收敛性和稳定性等价于系统(9)跟踪问题的收敛性和稳定性,证明过程不再赘述。 LOS 视线法是近年来应用较广的一种航向制导方法,其原理简单易懂且制导效果优异,因此选择LOS 视线法作为底栖式AUV 的航向制导方法。LOS 制导律有基于前视距离的制导以及基于视线圆的制导2 种形式。基于前视距离的制导律制导效果取决于前视距离的选取,制导效果一般,而基于视线圆制导律的制导效果与视线圆半径的选取有关,选取合适的视线圆半径可以实现较好的航向跟踪控制效果,故文中选择后者,其基本原理如图7 所示。 图7 基于视线圆的LOS 制导律示意图Fig.7 Schematic diagram of LOS guidance law based on line of sight circle 以AUV 为中心,定义一个半径为R的圆,R需要大于当前跟踪误差ye,以保证视线圆与当前跟踪路径始终有交点,交点的方向即为目标航向。基于这一特点,选用文献[7]所设计的一种视线圆半径选取方法,其形式为 式中:Rmin为最小视线圆半径;a、c均为正常数。当a≥1,c≈0时,有 根据式(31)可以看出,视线圆半径始终大于或等于交叉跟踪误差,此方法可以保证视线圆与当前航向始终存在交点。 视线圆型LOS 制导律下的目标航向角为 将式(6)对时间t求导,并将式(3)代入,可得 当设计合适的航向控制器,使AUV 的实际航向收敛于视线圆制导律下的目标航向时,有 选取李雅普诺夫函数为V=1/2ye2,将V对时间t进行求导,并将式(32)代入,有 由李雅普诺夫稳定性原理可知,交叉跟踪误差全局渐进稳定,即 传统的AUV 路径点跟踪控制通常都是使AUV以恒定的纵向速度运动。由于路径跟踪对AUV的运动速度没有太多要求,因此选用的是常规MFAC 航速控制器对AUV 的运动速度进行控制,航速控制器表达为 式中:τu(k)为AUV 在k时刻的纵向推力,∆τu(k)=τu(k)−τu(k−1)表示推力在2 个节拍内的差值;为伪偏导数φu(k)在k时刻的估计值;µu>0,λ>0为权重因子;ηu∈(0,1]、ρu∈(0,1]为步长因子。由于航速控制器的稳定性证明与航向控制器一致,在此不再赘述。 为了满足路径跟踪控制的快速性,通常设置的航速不会太低,一般在2 kn 左右。而当AUV 经过路径拐点处开始切换到下一路径时,较高的航速会导致AUV 在拐点处产生较大的偏航距离,因而改变期望的航向角,从而产生较大的航向超调,并影响路径跟踪的精度。如果减少切换半径,可以较好地解决问题,但同时也会减少AUV 对指定路径的跟踪精度,增加AUV 碰撞的风险。 针对这一问题,文中提出了一种双曲正切型航速制导策略,其表达式为 式中:ud为AUV 的期望速度,通常为定值;ω为正常数;dis(k)为AUV 在k时刻与当前跟踪路径点之间的距离。 由图可知,当函数自变量的绝对值超过2 时,函数的因变量恒为1;而当函数的自变量在0~2 之间时,函数的因变量在0~1 之间呈正相关变化。选取适当的系数 ω,当底栖式AUV 距离当前跟踪路径点的距离大于某个阈值时,tanh 函数的值恒为1,因此AUV 将保持定速运动。而当底栖式AUV 距离当前跟踪路径点的距离小于某个阈值而大于路径点切换半径时,期望的航行速度会随着AUV 与路径点之间距离的减小而不断减少,但会保持在原来期望航速的一半以上。AUV 航行速度的降低将会产生较小的偏航距离以及目标航向角变化,因此在路径点处的航向超调将会减少。当达到切换半径后,由于路径点发生切换,新的跟踪距离使得双曲正切函数的值继续等于1,AUV 的期望速度将会恢复到原来的恒定值从而继续保持定速运动,这将使得路径点切换时的减速对整个跟踪过程影响较小。 与传统的定速控制相比,文中所设计的双曲正切型航速制导策略,可以减少LOS 制导律下路径点切换时可能引起的航向控制超调,并增加路径跟踪控制的精度。 外场试验所使用的底栖式AUV 为实验室自主研发的FSN-1 号,如图8 所示。FSN-1 号配有垂推、侧推、主推等多个推进器,每台推进器满功率下可以提供150 N 的推力,从而实现多个自由度的运动。此外,还配有姿态传感器、无线电台、GPS、深度计和高度计等外部传感器。试验地址位于吉林市松花湖景区。 图8 FSN-1 号底栖式AUV 试验平台Fig.8 Test platform of FSN-1 benthic AUV AUV 的硬件组成如图9 所示。底栖式AUV共搭载了姿态传感器、高度深度计、USBL、无线模块、GPS 传感器等硬件设备,满足了基本运动控制的需要。AUV 的软件系统如图10 所示。从图中可以看出,AUV 在传感器接收状态的基础上,可以根据控制指令实现不同的控制任务,并驱动执行器完成任务。 图9 FSN-1 号底栖式AUV 硬件组成Fig.9 Hardware composition of FSN-1 benthic AUV 图10 FSN-1 号底栖式AUV 软件系统Fig.10 Software system of FSN-1 benthic AUV 为了验证文中设计的IMFAC 有效性与优越性,将该方法与文献[11]所设计的RO-MFAC 航向控制算法进行了对比实验。各控制器都经过参数调优处理,控制器参数如下。 1) IMFAC 2) RO-MFAC 试验的期望航向为−90°,试验结果如图11 和图12 所示。 图11 RO-MFAC 方法下−90°定向控制Fig.11 −90° directional control under RO-MFAC method 图12 IMFAC 方法下−90°定向控制Fig.12 −90° directional control under IMFAC method 从图11~图12 可以发现,航向从180°向−180°发生了突变,这是因姿态传感器的量程为±180°所引起。不难看出,RO-MFAC 控制方法在稳定后振荡幅度较大,出现了上文所提及的“积分累加”问题,航向误差接近±15°,而IMFAC 控制方法较好地解决了这一问题,其收敛时间及稳定性均略优于RO-MFAC 航向控制器。因此可以得出:改进MFAC航向控制器具有较好的控制效果,可以将其用于路径点跟踪控制试验。 基于上文提出的IMFAC 航向控制算法,将基于双曲正切型航速调整策略下的路径跟踪算法(改进方法)与传统的LOS 制导律下的路径跟踪控制算法(传统方法)作了路径点跟踪对比试验,所跟踪的路径为8 个路径点形成的梳状路径。 试验的路径点切换半径Rt为3 m。航速调整策略的参数为ud=0.9,ω=0.07。 试验结果如图13~图20 所示。 图13 传统方法下的路径点跟踪控制曲线Fig.13 Waypoint-tracking control curves under traditional method 从图13 和图14 中可以看出,传统的路径点跟踪控制在路径点切换处,由于航速较大导致转弯半径过大,出现了较大的超调,影响控制精度。这一点在图15 中更为明显,转弯处的超调较大,跟踪效果不太理想。从图16 与图20 的对比中发现,基于双曲正切型变航速调整策略的速度在拐点处明显变缓,这也间接引起图17~图19 中路径点跟踪控制器在转弯时偏航距离的减少,此外航向控制收敛速度也得到了明显的改善,因此加快了跟踪误差的收敛。 图14 传统方法下偏航距离曲线Fig.14 Yaw curves under traditional method 图15 传统方法下航向角跟踪曲线Fig.15 Course angle tracking curves under traditional method 图16 传统方法下速度曲线Fig.16 Velocity curve under traditional method 图17 改进方法下路径点跟踪控制曲线Fig.17 Waypoint-tracking control curves under the improved method 图18 改进方法下偏航距离曲线Fig.18 Yaw curves under the improved method 图19 改进方法下航向角跟踪曲线Fig.19 Course angle tracking curves under the improved method 图20 改进方法下速度曲线Fig.20 Velocity curves under the improved method 文中设计了一种基于MFAC 方法下的底栖式AUV 路径点跟踪控制器。首先,针对传统MFAC方法应用于航向控制所固有的积分效应问题,提出了一种改进型MFAC 控制器,并证明了控制器的收敛。接着,针对传统LOS 制导下的路径跟踪算法在路径点切换处超调较大的问题,设计了一种双曲正切型变航速调整策略。最后,利用FSN-1 号试验平台,进行了航向控制和路径点跟踪控制试验。通过试验证明,改进的MFAC 航向控制器效果优异,且双曲正切型变航速调整策略可以减少路径点跟踪控制过程中路径切换处的超调,加快控制误差的收敛,具有较高的工程应用价值。



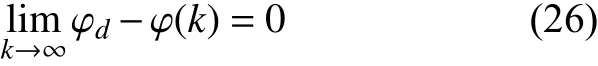

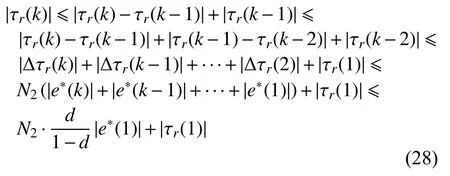

2.3 航向制导律选取及稳定性分析

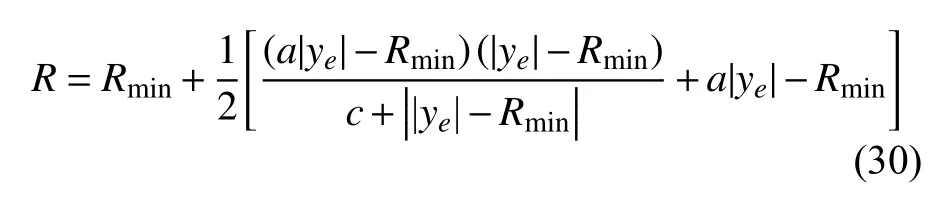
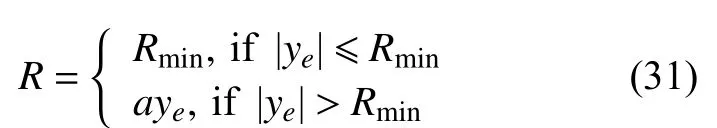
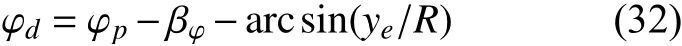


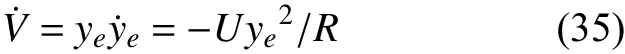

2.4 双曲正切型底栖式AUV 航速制导策略
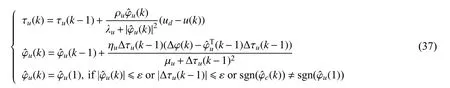

3 外场试验与结果分析
3.1 试验平台

3.2 控制系统软硬件
3.3 航向控制对比试验


3.4 路径点跟踪控制对比试验







4 结束语

