基于MCMC方法的区间控制伪装缺失值检测算法
史金余 孙禹明 谢 兄 刘卫江 滕俊凯
(大连海事大学大学信息科学技术学院 辽宁 大连 116026)
0 引 言
在大数据应用快速发展的今日,脏数据渐渐地成为数据分析的一大障碍,不仅会误导我们的工作行为,还可能造成巨大的经济损失。为了减少脏数据带来的严重影响,数据清洗在数据处理的过程中起着越来越重要的作用。数据清洗[1]是一个检测、诊断和编辑脏数据的过程。近几年研究表明,在进行数据清洗时,离群点检测技术成为了一种被广泛应用的数据识别技术,如工业损伤检测[2]、网络入侵检测[3]、欺诈检测[4]、临床医学检测[5]和地质探测[6]等。
为了提高检测效率,现在很多研究都对离群点进行了分类[7],在所有类中,对伪装缺失值的检测成为了一个难题,尤其是在数据范围内随机分布并在数据集中经常使用的有效值(以下简称有效值类伪装缺失值)。因此在本文主要讲解数据集中有效值类伪装缺失值的检测方法,目前已有很多学者采用了不同的方法对伪装缺失值检测问题进行了相关研究。Hua等[8-9]提出了DiMaC算法,该算法提出了一种嵌入式无偏样本启发式算法来检测伪装缺失值;Pit-Claudel等[10]提出了dBoost算法,该算法利用元组扩展来检测各种数据集中的离群点;Qahtan等[11]提出了FAHES算法,该算法主要是将伪装缺失值分成outlier和inlier两类采用不同的方法进行检测。三种算法中,dBoost算法并非主要检测伪装缺失值,因检测范围过大,会检测到非伪装缺失值,而DiMaC算法解决了此问题,但其运行时间较长。FAHES算法进行了分类检测也缩短了运行时间,但由于分类不够细致,仍然会有很多种类的错误出现在分类之外。对上述三种算法的研究发现,其检测效果不好的主要原因在于检测范围问题。为了提高检测效率,本文提出一种基于MCMC方法的区间控制伪装缺失值检测算法,来解决检测范围带来的麻烦。
在庞大的数据集中,为了在进行数据分析时取得良好的结果,非常有必要进行伪装缺失值检测,而本文算法主要采用MCMC算法和基于统计学的离群点检测算法,如果想有效地使用两种算法将面临如下挑战:
(1) 在检测中使用对基于统计学的离群点检测算法的改进来确定控制区间进行检测,但数据集中存在异常点,这必然会导致数据集的相关参数的变化,直接使用这些参数必然会产生一些误差,因此需要解决如何减少参数引起的误差问题。
(2) 从检测范围的角度来提高检测效率,主要通过缩小检测范围来提高检测效率,因此需要解决如何聚焦检测范围的问题。
本文主要贡献是提出一种新的检测算法,将MCMC方法和基于统计学的离群点检测算法进行相应的改进后结合起来检测,具体如下:
(1) 使用恰当的MCMC方法对参数进行采样,以解决由参数引起的错误问题。在使用MCMC方法时,选择了随机游走的M-H算法,并对其进行了相应的改进,使用格里汶科定理和Jeffreys先验方法来克服求解分布函数和先验分布函数的困难。
(2) 使用基于统计学的离群点检测算法来解决检测范围的问题。在使用基于统计学的离群点检测算法时,通过对控制区间进行相应的改进,以此克服区间过大等困难。
1 相关工作
1.1 伪装缺失值
目前,随着离群点检测技术的广泛应用,许多研究都是先对离群点进行分类后再进行检测[11-13],大大提高了检测效率。Pearson[14]提出的一个新出现的数据质量问题——伪装缺失值,它是一种特殊的缺失数据,指的是数据条目中不完全缺失但不能反映的值。文献[14]对伪装缺失值的分类具体如下:
(1) 超出范围的数据值,例如在只接受负值的正值的属性中隐藏缺失的值。
(2) 异常值,例如用非常大的值或非常小的值来伪装缺失的值。
(3) 在使用的键盘上具有重复字符或彼此相邻的字符,例如用5555555555代替一个电话号码。
(4) 不协调数据类型的值,例如用数值伪装缺失的字符串,反之亦然。
(5) 在数据范围内随机分布并在数据集中经常使用的有效值。
在上述每一种情况下,伪装缺失数据都可以被视为outlier(案例(1)-案例(4))或inlier(案例(5))。本文主要讲解上述伪装缺失值的第五种情况的检测方法。
1.2 MCMC方法
MCMC方法[15]主要包括Metropolis-Hastings算法(M-H算法)和Gibbs算法。其中M-H算法[16-19]是MCMC方法的核心,主要用于数据采样。算法主要由以下三部分组成:
(1) 从建议分布生成建议(或候选)样本。
(2) 基于建议分布和联合密度,通过接受函数计算接受概率。
(3) 以概率接受建议(候选)样本,或拒绝该样本。
建议分布主要分为对称分布和非对称分布两种,如果满足式(1),则建议分布为对称分布,否则为非对称分布。
q(xi|xi-1)=q(xi-1|xi)
(1)
对称分布包括高斯分布、以链当前状态为中心的均匀分布等;不对称分布包括F分布等。
根据M-H算法的特征,给出了任一分布作为建议分布的似然函数(密度函数)、先验分布和后验分布。
根据建议分布,可以得出其先验分布、似然函数分别为:
fp(xi)=prior(xi)
(2)
fl(xi)=likehood(xi,μ)
(3)
最后,根据先验分布与似然函数的乘积确定后验分布:
f(xi)=fp(xi)×fl(xi)=prior(xi)×likehood(xi,μ)
(4)
根据后验分布函数,可以得到接受函数为:
α(xi|xi-1)=min{1,q(xi-1|xi)π(xi)/
q(xi|xi-1)π(xi-1)}
(5)
根据式(5),决定接受还是拒绝该样本。
1.3 基于统计学的离群点检测算法
离群点检测的统计学方法[20]的一般思想是:学习一个拟合给定数据集的生成模型,然后识别该模型低概率区域中的对象,把它们作为离群点。离群点检测的统计学方法可以划分成参数方法和非参数方法两个主要类型,根据数据集以及实验需求进行分析,最终选择基于正态分布的一元离群点检测方法。
该方法主要分为两个步骤:
(1) 利用最大似然函数:
(6)
(7)
(8)
(2) 遍历样本集合,检测样本是否落在以下区间内:

(9)
该区间包含了大量的数据,所以如果样本在区间内,则为正常点,否则为离群点。
2 基于MCMC方法的区间控制伪装缺失值检测算法
由于数据集有很多脏数据,导致数据集的参数会发生变化,如果直接利用参数对数据集进行分析,误差就会很大。因此,本文将MCMC方法和基于统计学的离群点检测算法结合,提出基于MCMC方法的区间控制伪装缺失值检测算法。本文的主要工作如下:首先采用M-H算法对参数进行采样,然后根据采样出来的参数通过基于正态分布的一元离群点检测算法选取控制区间对数据样本进行遍历。算法的主要步骤如图1所示。
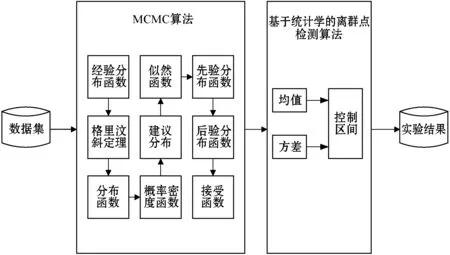
图1 本文方法的主要步骤
2.1 高频率伪装缺失值
为了使检测效果得到较好的改善,对1.1节中的伪装缺失值进行了进一步分类处理。以data.gov.uk数据集中Accident表中的部分数据为例来说明1.1节中伪装缺失值的第五种类型,如表1所示。
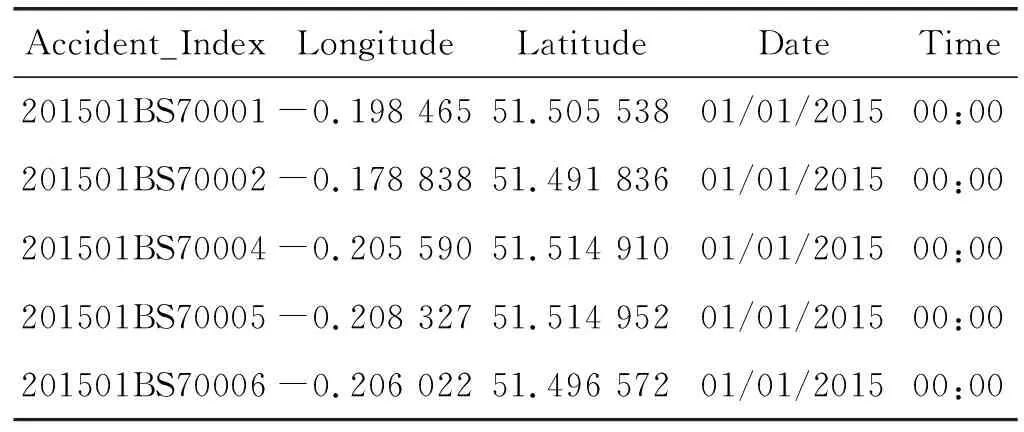
表1 data.gov.uk数据集中Accident表
可以看出,在Date列和Time列中,它们的值全部为01/01/2015和00:00,数据类型完全符合数据属性,完全发现不了是错误值。但当与真实数据进行对比时,会发现数据值是错误的,这种就是在数据范围内随机分布并在数据集中经常使用的有效值(第五类)。此种伪装缺失值给检测工作带来了巨大困难,它以一定的概率出现在正确值中,不容易被检测到。因此本文主要对该种伪装缺失值进行讲解,并重新命名为高频率伪装缺失值。
2.2 参数采样的方法(MCMC方法的改进)
当使用MCMC方法时,选择的是M-H算法。M-H算法主要分为独立抽样的M-H算法、单变量的M-H算法和随机游走的M-H算法,其中随机游走的M-H算法[19]是MCMC方法中应用最广泛的一种算法,通用性比较强,任何一种对称分布都可以作为该算法的建议分布,由此产生的马尔可夫链通常是遍历的,所以本文选用的是随机游走的M-H算法。
在使用随机游走M-H算法时,最困难的问题是求数据集的概率密度函数和后验分布函数。为了解决这两个问题,本文的方法如下:
(1) 利用经验分布函数和格里汶科定理确定分布函数,进而得到概率密度函数。
(2) 统一利用Jeffreys先验确定方法确定先验分布函数,得到后验分布函数和接受函数。
接下来,以高斯分布为例来讲述求解改进的M-H算法执行的主要过程,即参数采样的主要过程。
Step1经验分布函数。
定理1(格里汶科定理[21]) 设x1,x2,…,xn是取自样本总体分布函数为F(x)的样本,Fn(x)是其经验分布函数,当时n→∞,有:
(10)
定理1表明,当n相当大时,经验分布函数Fn(x)是总体分布函数F(x)的一个良好的近似。
在求概率密度函数时,首先求出了经验分布函数,由于数据量比较大,根据格里汶科定理,由经验分布函数近似得到了分布函数,进而通过分布函数得到了数据集的概率密度函数。
Step2建议分布。
在使用M-H算法时,首先需要确定建议分布类型,然后根据建议分布的不同类型,进行求解。
假设样本服从高斯分布:
xi~N(μ,σ2)
(11)
进而可以得出其密度函数:
(12)
然后,根据密度函数可以得到似然函数:
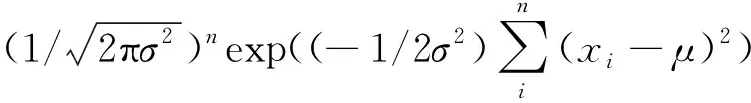
(13)
Step3先验分布函数。
先验分布函数的求解采用的是Jeffreys先验确定方法[22]。首先,对样本的似然函数取对数:
(14)
l(μ;σ2)=lnL(μ,σ2)=-n/2ln(2π)-
(15)
然后,求Fisher信息矩阵:
(16)
采用E(·)矩母函数方法[23]进行求解式(17)。
(17)
解得:
(18)
所以:
detI(μ;σ)=2n2σ-4
(19)
最后,根据先验分布函数的求解公式:
π(θ)=[detI(θ)]1/2
(20)
解得样本的先验分布函数为:
(21)
Step4后验分布函数。
根据似然函数和先验分布函数的乘积,得出后验分布函数:

(22)
Step5接受函数。
为了简化计算,方便对接受函数进行化简,在此考虑建议分布是否为对称分布,主要采用偏度来进行判断,具体如下。
偏度[23]是样本数据分布偏斜方向和程度度量,是样本数据分布非对称程度的数字特征,计算公式为:
sk=E[(x-μ)3]/σ3
(23)
(1) 当sk=0,样本数据为对称分布。
(2) 当sk≠0,样本数据为非对称分布,如果sk>0,样本数据为右偏,sk<0样本数据为左偏。
如果建议分布是对称分布,根据式(1),可以将接受函数简化为:
α(xi|xi-1)=min{1,π(xi)/π(xi-1)}
(24)
最后,根据接受函数,来决定接受还是拒绝样本。
2.3 控制区间的确定方法(基于统计学的离群点检测算法的改进)
本文主要检测高频率伪装缺失值,因此本文根据M-H算法传过来的参数,对基于统计学的离群点检测算法进行反向应用,并对控制区间进行改进,将一个大区间分成几个小区间的并集来控制数据遍历,进而提高检测效率。
具体方法如下:
Step6控制区间。
根据M-H算法所采样到的参数,确定两个区间:式(9)和式(25)。
(25)
第一个区间为根据基于统计学的离群点检测算法确定的区间,第二个区间为置信区间[21],置信度越大,置信区间越宽,通过调整置信度,控制区间,详细说明如下:
当样本x分布未知,但样本数据较大时,根据中心极限定理,它可以近似为:
(26)
当σ2已知时,则μ的置信度为1-α的置信区间为:
(27)
当确定了两个区间时,通过分析这两个区间,发现区间如式(9)包含的数据样本多于区间如式(28)的。
(28)
因此,将区间拆分成多个小区间并集,表示为:
(29)
确定小区间后,判定是否处于这些区间内:
(30)
如果一个数据样本处于上述区间(式(30))中,则为高频率伪装缺失值,否则为正确值。
通过对各种分布的分析,对高斯分布的计算一目了然。这里以高斯分布为例进行说明。
当样本分布为高斯分布时,区间式(9)将包含99.7%的正确数据,区间式(28)将包含95%的正确数据,因此区间式(9)比区间式(28)包含更多的数据。为了提高算法的精确度,根据数据样本分布不同,通过设置不同的置信度来控制控制区间,其中不规格分布置信度设置为75%,规格分布置信度设置为85%(包括正态分布、卡方分布、t分布等)。
2.4 算法描述
首先通过改进的M-H算法对参数进行采样;然后根据改进的M-H算法传过来的参数,通过改进的基于统计学的离群点检测方法确定控制区间式(31)。最后,在控制区间式(31)内,对数据对象进行遍历。本文主要检测高频率伪装缺失值,如果数据对象在控制区间内,则判定为高频率伪装缺失值;否则,判定为正常值。算法执行过程如算法1所示。
算法1本文算法
输入:数据集X中的数据对象x。
输出:数据集X中伪装缺失值集合G。
1.forxinXdo
2.根据Jeffreys先验确定方法计算数据对象x的先验分布函数;
3.根据式(22)计算数据对象x的后验分布函数;
4.根据式(5)计算数据对象x的接受函数;
5.根据式(31)计算数据对象x的控制区间;
6.ifx∈区间式(31)
7.将数据对象x添加到伪装缺失值集合G中;
8.end if
9.end for
10.输出高频率伪装缺失值集合G
3 实验验证
3.1 相关定义
为了能够明显地看出实验效果,定义了三个评价指标,即查准率(precision)、查全率(recall)和F1-Measure。设输入的样本总数量为m,输出的高频率伪装缺失值的数量为n,检测到的高频率伪装缺失值的数量为o。具体计算公式如下:
(1) 查准率(precision),记为P:
P=o/n
(31)
(2) 查全率(recall),记为R:
R=o/m
(32)
(3) F1-Measure,记为F1:
F1=(2PR)/(P+R)
(33)
相对而言,如果算法的查准率、查全率和F1-Measure都比较高,则证明该算法优于其他算法,具有良好的可用性。
3.2 数据集选择
为了验证算法的检测效果,并考虑到数据分析在各个领域的责任的重要性,本文选择Mass.gov数据存储库中3张表、UCI-ML数据存储库中4张表和Data.gov.uk数据存储库中6张表,共13个数据集进行比较实验,主要涉及医疗、交通和教育等领域。在进行实验前手工注释了每个数据集中的高频率伪装缺失值。
3.3 实验对比
实验从四个方面测试了本文算法:Ex-1:算法的效率(查准率、查全率和F1-Measure);Ex-2:与dBoost算法的比较;Ex-3:与DiMaC算法的比较;Ex-4:与FAHES算法的比较(Random DMVs);Ex-5:与k均值聚类算法的比较(KMOR算法)。
(1) Ex-1:算法的效率(查准率、查全率和F1-Measure)。为了验证本文算法的效率,在Mass.gov、UCI-ML和Data.gov.uk三个数据存储库中所选择的数据集上进行了相应的实验。为了方便进行实验,首先通过数据样本映射的方式对数据集进行分析,通过分析得到data.gov.uk数据存储库上所选择的数据集呈正态分布,Mass.gov和UCL-ML数据存储库上所选择的数据呈不规则的分布。通过对数据集的分析,可以知道在data.gov.uk数据存储库上所选择的数据集进行实验会比较容易些,可以直接得到数据样本的概率密度函数,根据概率密度函数求出似然函数,再根据似然函数求出先验分布函数,在进行求解先验分布函数时,由于数据样本所属分布不同,求解先验分布函数不够准确,导致实验效果不好,而本文所采用Jeffreys先验确定方法,它在不同分布中无信息即可确定先验分布函数,提高了检测效率和算法执行所用的时间。根据似然函数和先验分布函数计算出后验分布函数和接受函数,并通过接受函数得到所需要的样本均值和样本方差,并将置信度设置为85%,最后通过区间式(9)和区间式(28)确定区间并在区间内对数据样本进行遍历。而Mass.gov和UCL-ML数据存储库上所选择的数据集呈不规则分布,无法直接计算出概率密度函数,导致无法进行实验,而经验分布函数和定理确定其分布函数,进而可以得到概率密度函数,然后一步步求出似然函数、先验分布函数、后验分布函数、接受函数,并通过接受函数得到所需要的样本均值和样本方差,由于是不规则分布,因此将置信度设置为75%,最后结合区间式(9)和区间式(28)所确定遍历区间对数据样本进行遍历。
因为本文算法所检测的目标是高频率伪装缺失值,它通常伪装成正确的值并以较高的频率(出现频率低于正常值的概率)出现在数据集中,用以往的离群点检测算法或伪装缺失值检测算法进行检测结果不尽人意,因为它们所能检测到的仅仅是离群点或低频率伪装缺失值,而高频率伪装缺失值常常被误认为正常值检测不到。而本文算法通过区间式(9)和区间式(28)确定了区间式(31),即控制区间,缩小了检测范围。让数据样本在控制区间内进行遍历,如果数据样本在控制区间内,则可以找出高频率伪装缺失值。
遍历数据样本结束后,根据式(27)和式(28),求出本文算法在Mass.gov、Data.gov.uk和UCI-ML三个数据存储库中13个数据集的平均查全率和平均查准率,如表2所示。
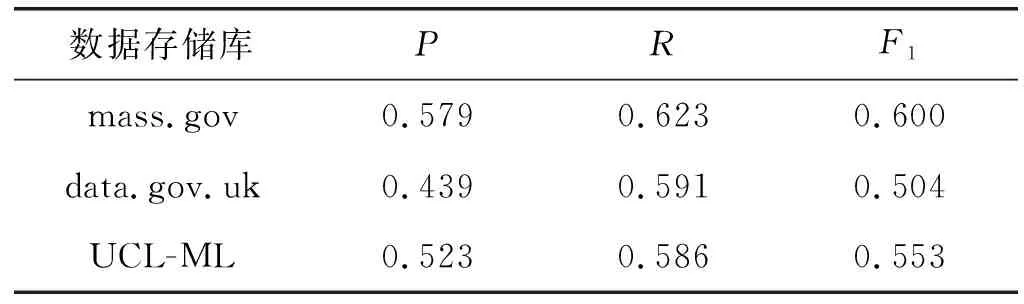
表2 三个数据存储库上的查准率、查全率和F1-Measure
(2) Ex-2:与dBoost算法的比较。dBoost算法并非为离群点检测而设计,进行检测时检测到非伪装缺失值,导致检测效果较差,而本文算法通过对控制区间的改进,缩小了检测范围,为检测伪装缺失值所设计,通过表3中的对比可以看出,本文算法的查全率提高了很多。

表3 与dBoost算法的对比
(3) Ex-3:与DiMaC算法的比较。DiMaC算法主要检测伪装缺失值,但是它没有对伪装缺失值进行分类,导致其检测范围太大,检测效率差,而本文算法对伪装缺失值进行了分类并且取得较好的检测效果。检测效果对比如表4所示。

表4 与DiMaC算法的对比
(4) Ex-4:与FAHES算法的比较(Random DMVs)。因为FAHES算法是对伪装缺失值分类后进行检测,所以它要优于前两种算法,但是由于分类不够细致,仍然会有很多的错误值出现在分类之外,导致检测效果略差,而本文算法的检测目标明确,主要检测高频率伪装缺失值,检测效果有很大的改善,如表5所示。

表5 与FAHES算法的对比
(5) Ex-5:与k均值聚类算法的比较(KMOR算法)。为了验证本文算法的权威性,选择了Gan等[26]优化的KMOR算法。由于本文主要检测高频率伪装缺失值,KMOR算法可能将所有伪装缺失值视为一个较大的簇,并将它们视为正常值,导致检测效果差。比较结果如表6所示,通过对查准率、查全率和F1-Measure的比较,本文算法的检测效果明显优于KMOR算法。

表6 与KMOR算法的对比
根据表3-表6中在Mass.gov、Data.gov.uk和UCI-ML三个数据存储库中查全率、查准率和F1-Measure的对比,绘制了对比图,如图2-图4所示。可以看出,本文算法优于其他四种算法。

图2 五种算法的查准率对比

图3 五种算法的查全率对比

图4 五种算法的F1-Measure对比
4 结 语
本文主要是解决检测高频率伪装缺失值的问题,为此本文提出基于MCMC方法的区间控制伪装缺失值检测算法,将改进的MCMC方法和改进的基于统计学的离群点检测算法结合在一起进行检测。首先采用改进的MCMC方法对样本进行参数采样,然后根据采样所得的参数采用改进的基于统计学的离群点检测算法确定控制区间,最后在确定的控制区间里对数据样本进行遍历。此外,利用Mass.gov、UCL-ML和Data.gov.uk三个数据存储库中的数据集进行对比实验,验证算法的权威性,通过实验结果可以看出,本文算法的查准率、查全率和F1-Measure有了明显改善。下一步,本文的工作将主要侧重于解决如何检测低概率的有效值类伪装缺失值,进一步提高算法的检测效果。

