一种基于局部模型对齐的动态视频修复方法
李灵俐 李晓明
(太原科技大学计算机科学与技术学院 山西 太原030024)
0 引 言
视频修复(video inpainting)是指替换或修改视频中有瑕疵的区域,或者是根据个人主观意志设定的某些区域,并且使得修复后的视频在视觉上有着令人愉悦的观赏效果。目前,摄像头固定不动时的静态视频修复已经获得了较大的成功,并已被嵌入一些商业软件之中。早期的视频修复算法多数沿用了图像修复的思路,即采用启发式思路在当前视频帧或图像库中查找最有可能的2D图像块(patch)来填充待修复区域[1-2]。然而这种单帧视频图像各自独立修复的方法,会导致修复后的视频出现帧间不连续或跳跃现象,因此,目前已经很少使用基于单帧图像的视频修复算法。近年来,视频修复的主流方法都是利用时空信息(spatio-temporal information)来实现的[3-5],并且取得了很大的成功。具体讲,填充待修复视频帧的图像块不再仅限于在2D图像空间查找,而是增加了时间维度,即查找相似块的操作是在3D空间实现的[6-7]。然而,这类方法要求视频拍摄时摄像机是固定的,如果摄像机有运动,那么在修复前必须先进行视频帧间的对齐操作。可以看出,为了将经典的静态视频修复方法[8-10]扩展到动态视频修复领域,视频对齐是必不可少的先期步骤。
对于摄像机运动时的动态视频修复也有一些相关的研究,但研究成果远没有静态视频修复成熟。例如,在动态视频修复中,文献[11-12]的方法采用把视频分割成移动前景和背景,用块匹配来实现运动估计。一旦移动的前景被绘制,背景根据块匹配估计的运动重新排列,背景是由复制和粘贴背景像素来填充以此达到修复的目的。文献[13-14]提出的方法也需要先分割前景与背景,然后在每一帧之间估计一组Homographies,并选择一个Homgraphy应用于所有的属于背景的每个被遮挡的像素。但是这两种算法都要求对背景和前景进行分割,此外,它们还有相当严格的像素限制,这意味着重新排列必须是极端准确的。虽然在这种极其小运动范围用Homgraphy模型的确可以近似模拟出视频帧的对应,但是对于更一般的情况,以上方法所使用的全局模型就会导致较大的误差。总体上说,目前的动态视频修复方法,或者需要进行前景背景的分割,或者其应用范围仅限于摄像头抖动这类微小运动的情况。
对于摄像机运动范围较大的情况,采用哪种对齐模型来补偿摄像机运动是一个重要的理论问题。众所周知,当摄像机运动是绕定点旋转或者场景是平面时,可以用全局Homography准确描述摄像机运动,当摄像机运动范围很小时,采用全局Homograph仍然可以较好地近似摄像机运动。然而,当摄像机运动不满足这些限制时,采用全局Homography近似摄像机运动会带来较大的误差,直接影响后续的视频修复。针对此类情况,本文给出一种基于局部模型对齐的方法,其基本思想是,将图像中的局部区域近似为一个小的平面,这样图像局部区域的运动可用一个Homography描述。对图像不同的区域采用不同的局部模型,从而提高视频帧的对齐精度。另外,局部模型的估计精度与局部邻域中特征点的数量和分布密切相关,本文采用当前性能较好的基于运动一致性的特征匹配方法,有效地增加了特征点的数量,从而提高了局部模型的估计精度。实验结果表明,本文方法不需要事先分割视频的前景和背景,对摄像机运动范围较大的视频修复问题,大大提高了视频对齐精度,相应地提升了视频修复的质量。
1 基于局部模型的视频帧对齐
如前所述,当摄像机运动满足一定的限制时,帧间图像满足全局2D单应矩阵(Homography)约束[15-16]。
1.1 全局模型对齐算法
设x=[x,y]T和x′=[x′,y′]T是两帧图像I和I′之间的对应点,那么描述两帧图像间的全局变换模型可表述为:
x′~Hx
(1)
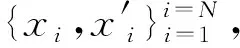
x′×Hx=03×1
(2)
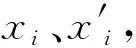
aih=02×1
(3)
式中:ai为2×9的矩阵;h=(h11,h12,h13,h21,h22,h23,h31,h32,h33)T是H矩阵的向量化形式。求解h需要至少4对对应点,如果对应点数量超过4对,可通过求解以下目标函数来得到式(4)中A矩阵经过SVD分解后最小奇异值对应的奇异向量即为h的解。更详细的解释可参看文献[17]。
(4)
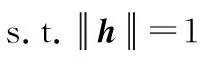
可以看出,基于全局模型的对齐算法是假设图像所有位置满足同一模型,而且上述模型估计过程是利用图像所有对应点求得的,且每组对应点具有相同的权重。对于满足一定运动限制的摄像机运动来说,全局模型准确反映了摄像机的运动,而且模型计算简单。然而,对于一般运动和一般场景下拍摄的视频,由于视差的存在,会导致较大的对齐误差,从而直接影响后续的视频修复精度。
1.2 局部模型对齐算法
为了解决全局单一模型在摄像机一般运动和一般场景下对齐出现重影和鬼影等问题,受文献[17]的启发,本文将基于局部模型对齐的方法与静态视频修复算法结合,使动态视频修复适用于更加一般的情况。
不同于全局模型,基于局部模型的对齐方法是对图像不同位置采用不同的对齐模型。其基本思想为:将每个局部区域近似为一个平面,这样每个区域可用一个单应矩阵描述其几何变换。这样,每个局部区域的几何变换可表示为:
(5)
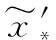
(6)
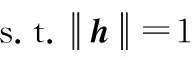
需要注意的是,不同于全局模型求解方法(式(4)),局部模型方法对每对对应点增加了一个权重因子项w*,具体为:
(7)
式中:σ是一个尺度参数;xi是第i个点匹配的一半的源图像I中的坐标。
直观地说,由于式(7)为接近x*的数据分配更高的权重,投影扭曲H*更好地尊重x*附近的局部结构。将其与式(1)进行对比,后者对所有x*使用单个全局H。此外,由于x*在其域I中连续移动,因此翘曲H*也平稳变化。这就产生了一个能够灵活地适应数据的整体扭曲,但试图保持扭曲的投影趋势,即灵活的投影扭曲,称之MovingDLT[17]的方法。
然后划分为单元,对源图像I中的每个像素位置x求解是不必要的浪费,因为相邻位置将产生非常相似的权重,从而产生非常相似的单应性。因此,将二维域I均匀地划分成一个由C1×C2个单元组成的网格,并以每个单元的中心为x*同一个单元中的像素将使用相同的同形法进行扭曲。图1观察到翘曲是全局投影外推,但在重叠区域灵活适应,以便更好地对齐。

图1 局部模型对齐
划分为单元可以有效地将WSVD实例的数量减少到C1×C2。另外,每一个WSVD实例都是相互独立的,因此一个简单的加速计算方法就是并行求解WSVD。即使没有并行处理,在Pentium i7 2.2 GHz四核机上,在包含2 100个筛选匹配项(A的大小为4 200×9)的图像中的所有100×100个单元求解也只需3 s。
一个潜在的问题是,单元间的翘曲可能会出现不连续,因为单元的分割有效地降低了平滑变化的权重。在实践中,只要单元分辨率足够高,弯曲不连续的影响最小。
最后进行图像的变换和重采样,这个步骤就是用计算出的投影函数,作用于输入图像上,然后采用适当的方法,计算出变换后的坐标像素值。
对于求解任一点x*处的局部模型,在式(6)中,每组对应点在其中的权重不同,且由式(7)可看出,离x*越近的对应点权重越大,反之,离x*越远的对应点权重越小。简言之,局部模型的估计主要是利用局部邻域点来估计的,而不是用图像所有点来估计的。
基于局部模型的对齐方法容易引起图像的局部变形不连续问题。然而,文献[17]的研究表明,这种现象并不突出。正因为此,在诸如图像拼接等应用中,基于局部模型的对齐方法也得到了广泛的应用。
2 GMS算法
虽然局部模型在具有一定视差时具有较好的对齐效果,但其对齐精度与特征点数量和分布的影响较大。本文尝试了Sift、Surf等多种局部特征点匹配算法,实验表明,这些经典的特征匹配方法常常会导致所匹配的特征点比较稀疏,直接影响图像的局部对齐性能。受GMS算法[18]启发,本文试图将GMS算法与局部对齐模型结合,来寻求更满意的对齐效果。
GMS算法是一种基于运动一致性的特征匹配算法。运动一致性假设是指,图像中相邻像素点具有相似的运动模式。文献[15]把这种运动一致性思想转化为更简单的统计方法,并取得了很大的成功。
GMS算法的基本思想很简单:正确匹配的特征点的对应关系通常在运动方面会表现出相同的一致性,而错误对应点之间则不会有这种一致性关系。因此,在正确的匹配关系周围可能会有更多的正确的匹配点支持,而错误的匹配对不具有这种规律性,而是具有随机性。
如图2所示,假设图像对Ia和Ib中狗的鼻子部位的匹配点xi是正确的,那么xi周围支撑区域a中的特征点更有可能匹配到相应的支撑区域b;反之,假设图像对Ia和Ib中狗的脚掌部位的匹配点xj是错误匹配,那么xj周围的特征点的对应匹配位置具有一定的随机性。基于这种运动一致性思想,文献[15]给出了一种基于统计的特征点匹配方法。首先将图像划分为一定大小的网格,如果对应网格中的匹配点数量超过预定的阈值,那么认为网格中的匹配是正确的,反之,如果对应网格中的匹配点较少,反映了对应点不符合一致性假设,因此被认为是错误匹配。根据这一思想来区分正确与错误匹配。
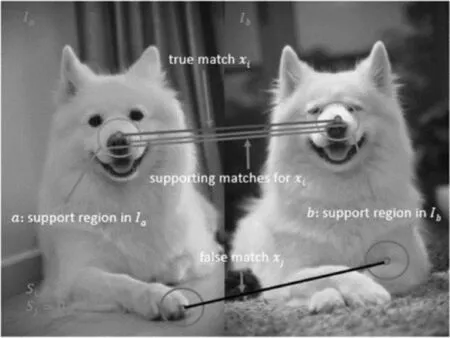
图2 GMS方法原理图
GMS算法提出后,近几年获得了很大的成功,目前已被集成到OpenCV库中。大量实验表明,基于GMS的特征匹配方法大大提高了对应点匹配数量,而且具有较高的执行效率,非常有利于基于局部模型的视频对齐,从而提升动态视频的修复性能。
3 实 验
3.1 评价指标
为了保证实验结果评价的客观性,本文采用常用的两种质量评价指标PSNR[19]和SSIM[20]对实验结果进行评价。
3.1.1PSNR
峰值信噪比(PSNR)是一种评价图像的客观标准。PSNR是最普遍、最广泛使用的评鉴画质的客观量测法,它是原图像与被处理图像之间的均方误差相对于(2n-1)2的对数值,定义为:
(8)
(9)
式中:MSE指均方误差;I和K分别代表处理前后的图像。PSNR值越大,就代表失真越少。
在视频对齐问题中,I和K分别代表两幅图像对齐后重叠区域的所有像素点的灰度值。
3.1.2SSIM
SSIM是用来衡量两幅图像相似度的一个常用指标,其值越大越好。作为结构相似性理论的实现,SSIM的计算是从图像X和图像Y的三项指标综合度量的,这三项指标分别为:亮度(luminance)、对比度(contrast)和结构(structure)。SSIM定义为:
(10)
式中:μx、μy分别表示图像X和图像Y的亮度均值;σx、σy分别表示图像X和图像Y亮度的标准差;σxy代表图像X和图像Y协方差;c1、c2为很小的常数,是为了避免括号内出现0而设定的。
在本文实验中,SSIM指标用来评价不同方法对齐后参考图像与目标图像之间的接近程度,该指标也可以用来评价修复前后的效果对比。
3.2 一般局部模型与全局模型对齐效果对比
为了比较局部模型与全局模型对齐效果,本文针对不同场景做了实验。在如下两组实验中,特征检测采用sift特征,特征匹配采用常用的最近邻与第二近邻的比值作为匹配准则,然后采用RANSAC方法去除错误匹配点。我们把这种方法称作一般局部模型匹配方法,方便与下一部分的匹配方法相区分。
图3的实验数据是航拍的河流与村庄,视频一共拍摄235帧,飞行器拍摄的路线跨度较大,相应的视频帧之间的视差也较大。图3列出第15和第35帧之间的对齐结果。可以看出采用全局模型对齐后的视频帧,屋顶和湖泊都有较大程度的重影问题,而采用局部模型的对齐效果比全局模型有了显著提升。从PSNR指标和SSIM指标的结果来看,局部模型对齐后的图像质量要高于全局模型对齐后的图像质量。

(a) 局部模型 (b) 全局模型图3 局部模型与全局模型对齐效果对比(实验数据1)
图4的实验数据是距离目标5 m拍摄的,场景中既有刚性的建筑对象,又有运动的人与背景,且拍摄场景不在同一平面,视频视差较大,实验场景较为复杂。该视频数据共有358帧,图4中列出第17与27帧的实验结果,其中:第一行两幅图像是待对齐的两帧图像;第二行是对齐后的全局模型对齐结果和局部模型对齐结果;第三第四行是放大后的细节。可以看出,全局模型对齐后的图像中男生的耳朵、鼻子等身体部位都有非常明显的模糊与重影现象,而局部模型对齐后效果有了明显改进。

(a) 全局模型 (b) 局部DLT模型图4 全局模型比与局部DLT模型对比(实验数据2)
因PSNR和SSIM指标(图5和图6)也可得出相同的结论。
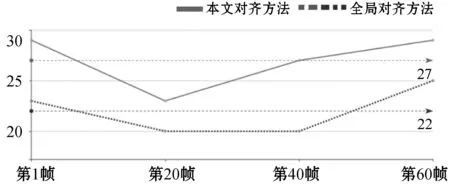
图5 PSNR指标对比(实验数据1)

图6 SSIM指标对比(实验数据1)
综合实验结果来看,由于局部模型和全局把模型本质上的算法特性,基于局部模型的Homography更适合描述大视差下的摄像机运动,基于局部模型的对齐效果都要好于全局模型对齐结果,从如图7和图8所示的实验也可看出,本文算法结果要好于以往以全局模型为代表[9]的实验结果。

图7 PSNR指标对比(实验数据2)
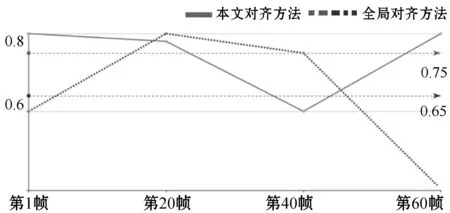
图8 SSIM指标对比(实验数据2)
3.3 GMS局部模型与一般局部模型的对齐对比
根据局部模型的计算过程可知,局部模型估计的精度与特征点的数量和分布密切相关。在实际应用时很多情况下常规的匹配方法得到的特征点比较少,这时采用一般局部模型,其对齐效果就会大打折扣。本节实验结果表明,将GMS特征点检测算法与局部模型结合,其对齐结果有了显著提高。
在图9中,最上面两行分别显示了采用一般匹配方法与采用GMS方法匹配后的对应点,显然GMS方法匹配数量要大大多于一般的方法。同时可以明显看出,特征点数量的多少对图像对齐的影响。比如,一般匹配方法对齐后其窗户和建筑已经严重变形,而GMS方法则取得了较好的对齐效果。
3.4 视频修复效果对比
文献[6]是一种经典的视频修复算法,并且得到了广泛的应用。该算法主要用于修复静态视频,对视差较小的动态视频,先采用全局仿射模型进行对齐然后再采用静态修复方法进行修复,取得了不错的效果,并且由于采用了改进后的三维patchMatch查找填充块方法,因此还具有较高的运算效率。在本节实验中,视频对齐采用基于GMS的局部模型方法,而视频修复采用了文献[9]中的方法。
图10中第一行是拍摄的图书馆建筑的视频样例帧,其中黑色区域是人工污染区域,我们试图修复这块区域。该视频是高度结构化场景,且具有较大的视差,视频修复具有较大的难度,如果对齐精度不高,很难保证良好的修复效果。图10中第二行左右两图分别是采用全局模型对齐和本文局部模型对齐后的修复结果。从修复后的放大图(第三行)可清晰看出,原图中门洞部分采用全局模型对齐后的修复结果明显出现了错误的填充,而本文方法得到的结果有了明显的改善。同样,PSNR和SSIM指标也给出了一致的结论。

(a) 文献[9]修复结果 (b)本文修复结果图10 文献[9]与本文方法修复结果对比
图11是另一段实验视频。运动视频中有一运动的老人和年轻男孩。该视频数据共302帧,图中黑色区域表示待修复的部分,本次实验目的是改变视频故事,即去除原来在视频中一直出现的年轻男孩,并且在去除男孩后,修复男孩原来所在的区域,得到在视觉上满意的结果。

(a) 全局模型修复 (b) 局部模型修复图11 全局模型与局部模型对齐效果对比
可以看出,采用文献[6]中全局模型对齐后的视频帧由于对齐不准,修复后的图像中紫色器材上出现明显错位和变形,而本文提出的基于局部模型的修复方法效果在视觉上取得了更加令人满意的结果。
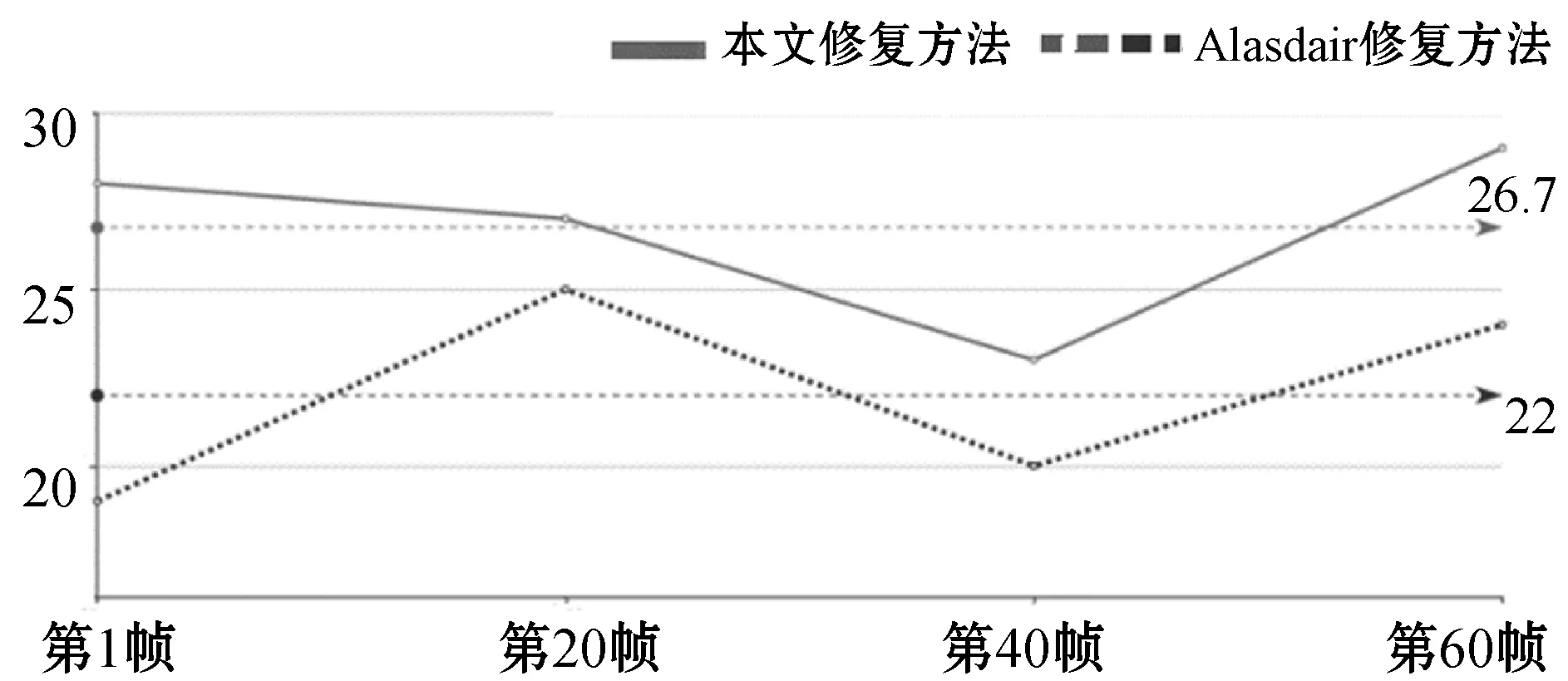
图12 文献[9]与本文方法PSNR指标对比

图13 文献[9]与本文方法SSIM指标对比
由图14和图15可以看出,PSNR指标和SSIM指标的均值(图中水平虚线标注的部分)本文的修复方法也都高于文献[6]的算法。
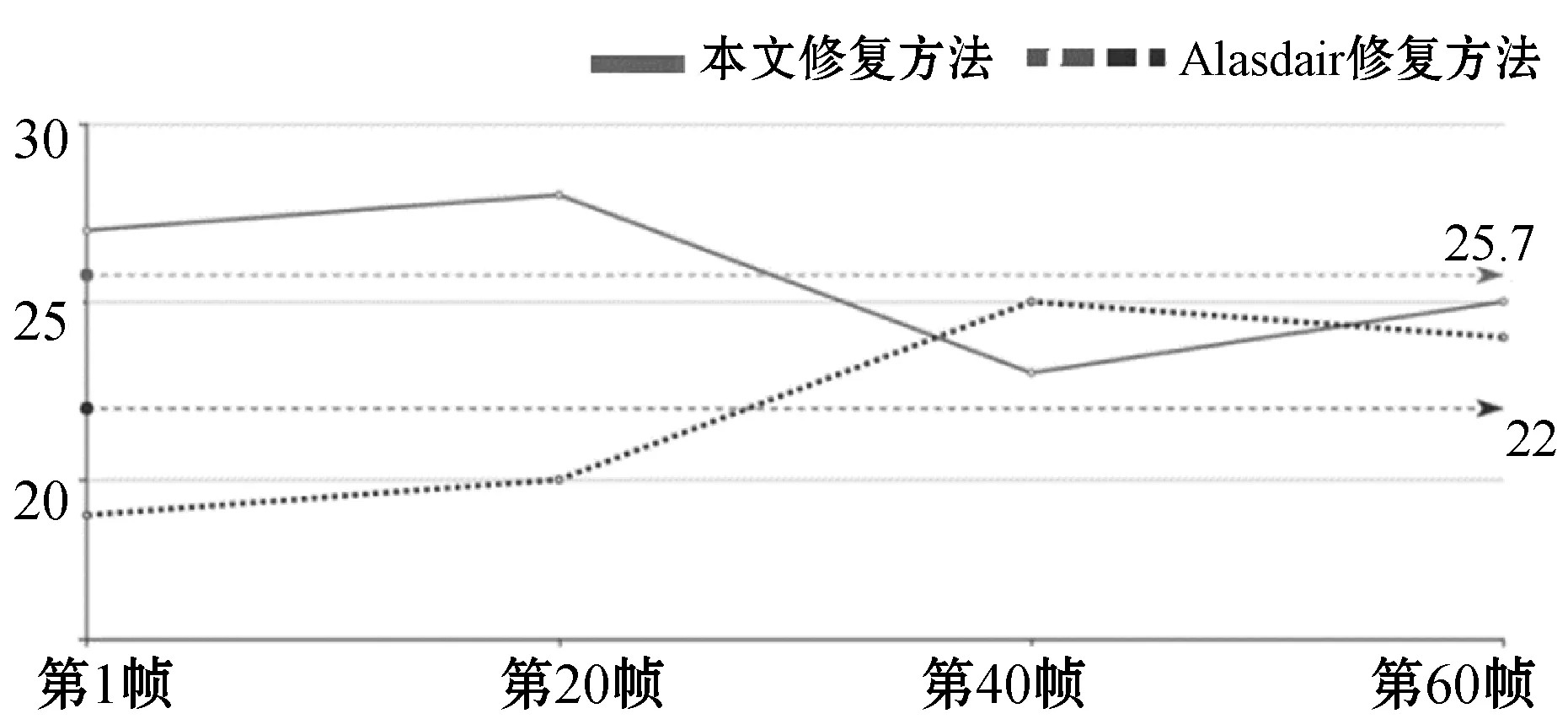
图14 全局模型与局部模型PSNR对比
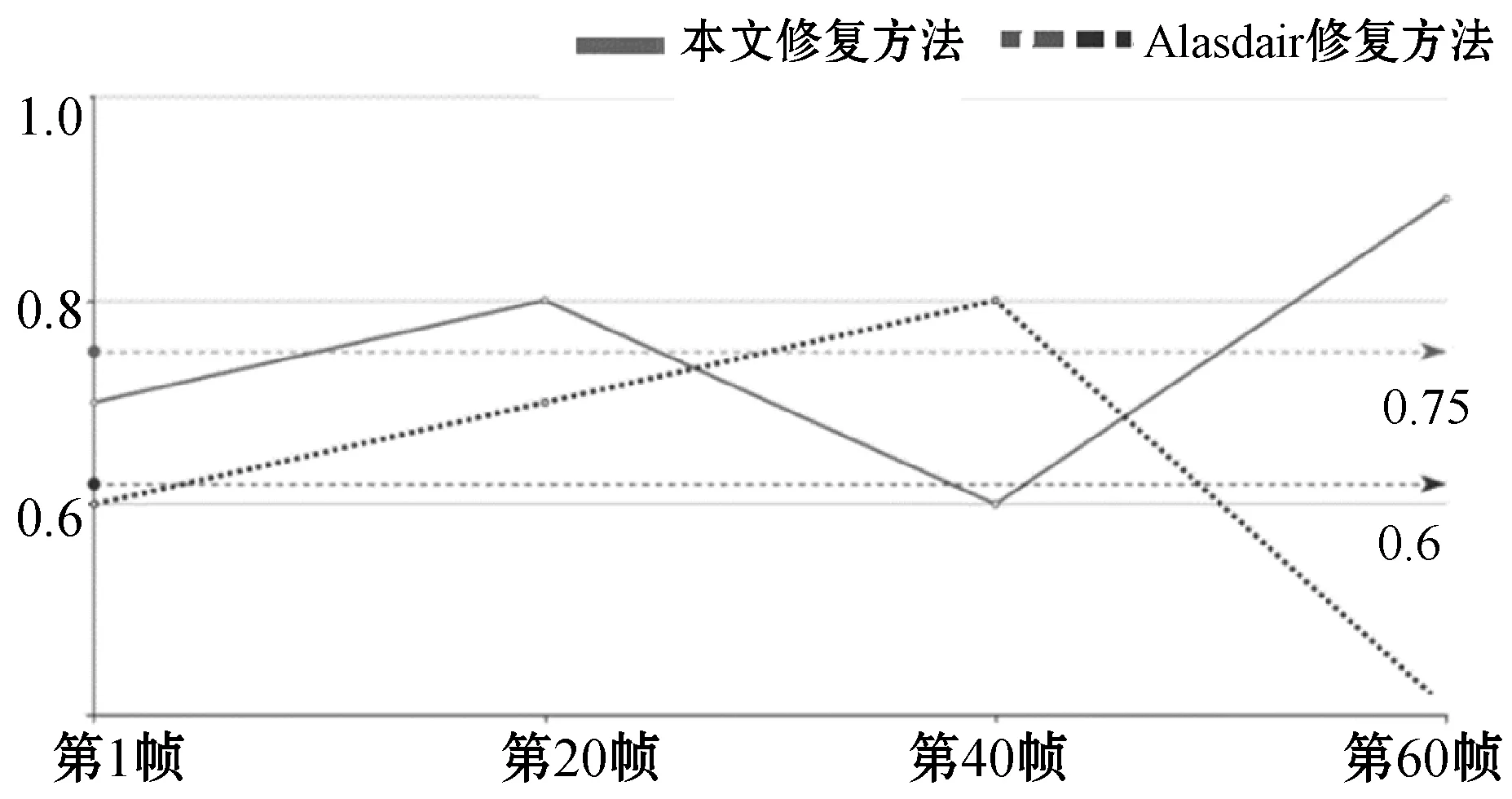
图15 全局模型与局部模型SSIM对比
为了对算法进行进一步的客观评价,本文还使用BSD数据集和Urban数据集对算法进行测试。其中:BSD数据集包含200对自然场景的图片,如图16所示;Urban数据集包含100对城市场景图片,如图17所示。测试结果如表1所示。可以看出,与Alasdair算法相比,本文算法在Urban数据集和BSD数据集上的结果的SSIM指标和PSNR指标均有所提高。

(a) Alasdair (b) 本文算法图16 Urban数据集上算法修复效果

(a) Alasdair (b) 本文算法图17 BSD数据集上算法修复效果
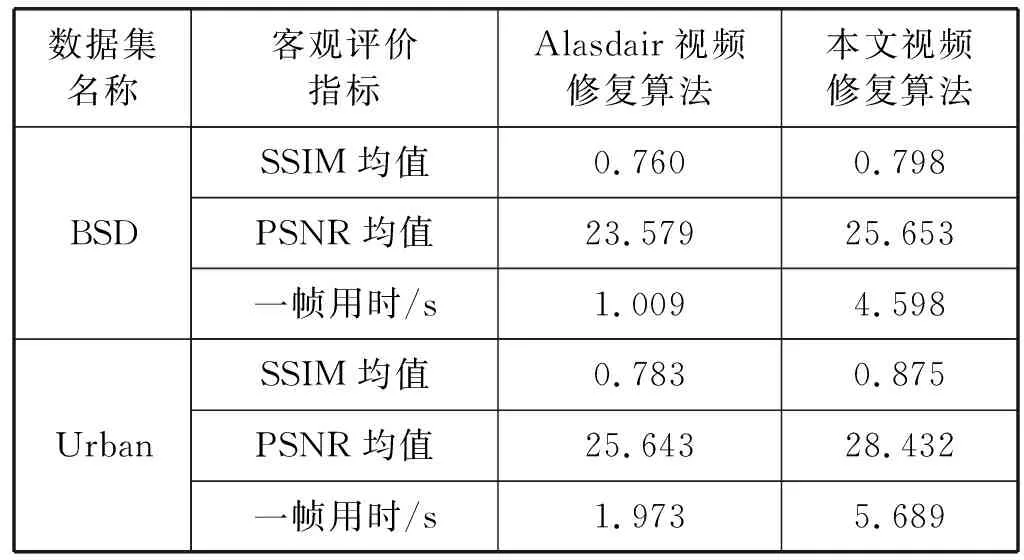
表1 在公开数据集上的实验结果
由图16、图17可以看出,本文的视频修复算法在BSD数据集和Urban数据集上都取得了更好的结果,由表1可以得出,本文算法比Alasdair算法在数据集上的表现更好,SSIM评价指标和PSNR指标都显示更高。但从时间上来说,本文算法的时间复杂度更高,花费时间更多。
4 结 语
本文针对视差大、视频背景复杂的动态视频修复问题,提出一种基于局部模型对齐的视频修复算法。由于局部模型能更好地描述摄像机的一般运动,因此,相比全局模型取得了更好的对齐效果;另外,本文采用GMS特征匹配方法,有效地增加了特征点匹配的数量,从而进一步提高了局部模型的估计精度。实验结果表明,通过提高视频对齐精度,扩展了传统静态视频修复方法的适用范围,有效地提升了动态视频修复性能。下一步我们将继续在对应点扩散、对应点的分布调整方面进一步研究,以进一步提升基于局部模型的对齐和动态视频修复性能。

