提高智能电网暂态稳定裕度的控制研究
韩红泉 陈 曜 陈世明
(华东交通大学电气与自动化工程学院 江西 南昌 330013)2(广州民航职业学院飞机维修工程学院 广东 广州 510403)
0 引 言
电力系统的暂态稳定性一直被认为是其安全运行的关键问题之一,电力系统韧性与电力系统安全性的传统概念相关联,即电网在发生物理偶发事件时仍能保持完整的能力[1]。在传统电网中,暂态稳定性极大地依赖于连接到电网的机器的惯性。随着常规的高惯性发电(如化石燃料发电)占比减少,利用风力和太阳能等低惯性发电占比增加,使得连接到电网的旋转机械总惯性趋于减小,从而降低了电网承受大扰动的能力。并且现代电网规模和复杂性不断增加,并产生了信息网络安全问题,使电网暂态稳定控制变得更具挑战性[2]。因此,被称为智能电网的现代电网受到信息干扰和物理扰动的影响,需要从网络物理系统(Cyber-physical Systems,CPS)角度考虑整体,制定稳定未来智能电网的新战略,提高电网暂态稳定裕度,以保证其暂态稳定性。
将电力系统类比为一个多智能体系统,分布式暂态稳定控制策略注重系统中多智能体之间的合作与协调,能够解决许多集中式[3-4]和分散式[5-6]难以解决的大规模复杂优化控制问题,发挥出智能电网的优势,并给出高效率控制约束[7-8]。Zhang等[9]采用分布式一致性控制方法,能够实现电力系统中合理的功率分配,增强电力系统稳定运行能力。文献[10]采用多智能体一致性理论,针对电力系统中的跟踪控制问题进行研究。文献[11]提出了一种多智能体一致性算法,用以解决电力系统的分层控制和功率分配问题。文献[12]将分布式算法应用于含分布式电源的微电网,实现了功率合理分配和频率稳定。
随着储能技术(Energy Storage Systems,ESS)、相量测量单元(Phasor Measurement Unit,PMU)、现代通信网络等新技术的应用[13-16],众多学者提出了将这些新技术与传统技术相结合的控制策略,以提高现代电力系统的性能。其中,储能技术越来越多地被布置到电网中,为稳定控制方法提供了新的思路。文献[17]将电力系统动力学方程与蜂拥算法结合,针对严重干扰后的发电机同步问题,进行蜂拥控制的研究,然而在建立模型时未考虑电力系统各节点之间的影响权重问题。文献[18-20]提出了一种分布式一致比例积分(Consensus Proportional Integral,CPI)控制器,通过控制具有快速动作特性的分布式储能装置来调节电力系统频率,加快电力系统暂态稳定恢复,提高电力系统的抗干扰能力。文献[21]设计一种非线性自适应控制器,通过分布式储能装置进行功率控制,减轻通信延迟等网络干扰对系统造成的影响,提高电力系统在的暂态稳定性。文献[22]提出了一种参数反馈线性化(Parameter Feedback Linear,PFL)控制器,利用飞轮储能系统对电网故障后进行暂态稳定恢复控制,提高电网暂态稳定裕度。文献[23]设计了一种自组织模糊神经网络控制器,利用飞轮储能系统来提高智能电网的暂态稳定性和传输能力。文献[24-25]设计了一种线性反馈最优(Linear Feedback Optimal,LFO)控制器,通过控制储能装置实现电网故障后的稳定控制,提高电力系统抗扰能力。
结合上述问题及研究现状,本文主要针对智能电网的线路故障和通信延迟问题,设计一种新的分布式控制器,其通过相量测量单元(PMU)接收电网的部分实时状态信息,并结合权重矩阵,实现局部信息交互,利用可控外部储能设备,向发电机母线中输出(或吸收)有功功率进行控制,快速高效地实现系统暂态稳定恢复,从理论分析和仿真两方面验证该控制器的有效性和快速性。
1 信息物理系统建模
1.1 多智能体一致性相关理论知识
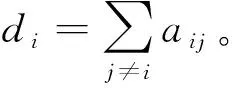
引理1[26]拉普拉斯矩阵L的特征值满足0=λ1(L)≤λ2(L)≤…≤λN(L)。当图G连通时,满足下式:
(1)
引理2[26]矩阵L是一个半正定矩阵,满足以下性质:
(2)
引理3[27]假设W∈RN×N是一个对称正定矩阵,W1∈RN×N是对称矩阵。对于任意向量x∈RN,有式(3)成立。
λmin(W-1W1)xTWx≤xTWx≤λmax(W-1W1)xTWx
(3)
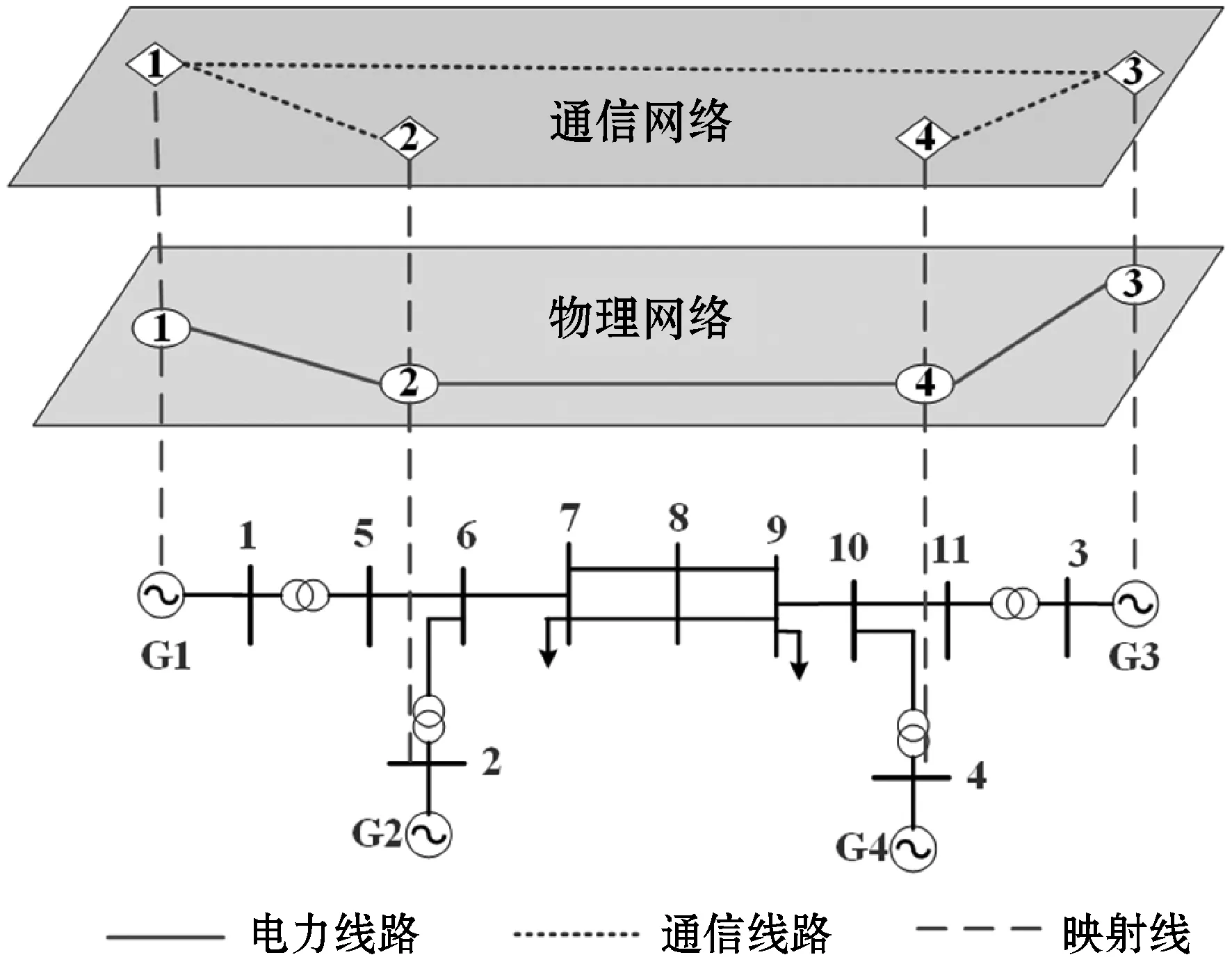
引理4(琴生不等式)对于任意常数矩阵U∈Rm×m,U>0,标量0 (4) 引理5[28]对于任何给定的实矩阵A、B,存在合适的S满足S=ST>0和一个标量ε>0,有: ATB+BTA≤εATSA+ε-1BTS-1B (5) 本节给出智能电网的分布式控制模型。将电力系统建模为一个双层结构的分布式控制模型。上层通信网络由多智能体(PMU、数据接收单元、本地控制器)组成,用于信息的传递、处理。下层物理网络由发电机、负荷及可控的分布式储能装置组成。以2区4机系统为例,拓扑结构如图1所示。 图1 2区4机系统双层模型 从多智能体系统视角来解决电力系统暂态稳定控制问题。每个智能体都包括一个发电机、PMU测量单元、本地控制器和分布式储能系统(DSS)。其中,PMU用于测量转子角度和转子速度,当前部署在电网中的DSS(例如飞轮或新型电池等)除了为上层的通信网络提供电能外,还可以向连接的总线注入/吸收有功功率,用于负载平衡和频率调节,而且周期要短得多,有利于实现控制的实时更新和执行。 (6) (7) 假设1假设信息物理系统网络拓扑图是连通的。 假设2gi(δi(t),ωi(t))对于ωi(t)是有界的,则存在常数hi,i=1,2,…,N,使得: (8) 针对电力系统,本文设计以下蜂拥控制协议: (9) 定义1定义势能函数Φ(x): (10) (11) 式中:c为常数且c>0;δij(t)=δi(t)-δj(t);(i,j)∈E表示发电机i和发电机j之间的相对功角。 定义2对于式(6)的系统,对于任意初始状态有: 则蜂拥控制是渐进实现的。 定理1对于系统式(7),在假设1和假设2成立条件下,存在常数ki>0,且ki满足式(12),则式(9)的控制协议可以有效地解决系统的一致性问题。 ki≥hi+λmax(L)i=1,2,…,N (12) 证明:构造Lyapunov函数为: V=V1+V2 (13) 对V1(t)求导得: (14) 或许小伊不知道,在他感慨着世俗的同时,另一个在他眼里生活的毫无尊严的家庭妇女正焦急地寻找他。不,严格地说那并不是他,只是他生命里软弱平庸的一部分——带着e人格的他。 (15) 对V2(t)求导得: (16) 将式(7)和式(9)代入式(16),可得: (17) 对Lyapunov函数V求导,由式(14)和式(17)可得: (18) (19) 由引理3、4、5可得: ωT(t)(H-K-L)ω(t)+ ωT(t)(H-K-L)ω(t)+ (20) 本文将所提出的分布式控制器应用到新英格兰39节点系统中,并在MATLAB/Simulink平台中进行仿真验证,其电力系统拓扑如图2所示。仿真实验中,电力系统在t=0.5 s时刻,线路16-17中的母线17侧发生三相短路故障,故障在t=0.6 s时刻清除,t=0.7 s时刻(即发生故障100 ms后)激活所有控制器,设置观察时长为10 s。为了评估所提出控制器的恢复能力,实验一中发生故障后,不加入任何控制,且仿真观察时间设置为3.5 s。在本文所有实验中,电力系统励磁稳定器(Power System Stabilizer,PSS)一直处于未投入状态,即PSS=0。本文中认为电力系统进入稳定运行状态的标准是发电机的转速误差在0.1%之内,即发电机的转速处于59.94 Hz和60.06 Hz之间[21]。 图2 新英格兰39节点系统分布式控制模型 实验一:观察所设置故障对系统造成的影响。系统发生线路故障后,不对电力系统施加任何控制,各发电机的转速和功角响应情况如图3和图4所示。可知各发电机功角差值超过5π/9,且转速波动较大,系统失去暂态稳定运行,并面临崩溃风险。 图3 未加控制时电机功角响应 图4 未加控制电机时转速响应 实验二:对比CPI控制器。文献[18-20]提出了应用CPI控制策略影响发电机机械功率的自动频率控制,该控制策略应用于两级:第一级根据参考转速调节发电机的实际转子转速;第二级更新参考速度以消除误差。CPI控制器表达为: (21) (22) 各发电机状态响应如图5和图6所示。由仿真结果可知,CPI控制器能够防止系统崩溃,所需稳定时间约为4.25 s,稳定时间较长。 图5 加入CPI控制器电机功角响应 图6 加入CPI控制器电机转速响应 实验三:应用本文设计的控制器。在本文设计的控制器作用下,系统中各发电机的转子动态曲线如图7和图8所示,其分别反映了加入本文控制器后,各发电机的功角和转速动态变化情况。本文设计控制器在故障发生后,所需暂态稳定时间约为2.8 s,对比图3-图6可知,该控制器能够快速响应系统故障,并可有效缩短稳定过程。 图7 加入本文控制器电机功角响应 图8 加入本文控制器电机转速响应 3.2.1储能设备容量限制 仿真结果如图9所示,在4%≤η≤7%的条件下,本文控制器使电力系统恢复稳定所需时间约为分散控制器[21]和PFL控制器[22]的一半;在η≥10%的条件下,三种控制器所需稳定时间无太大差别,说明本文设计的控制器在储能设备低容量的条件下有更好的控制效果。 图9 不同容量限制下的系统稳定时间 3.2.2通信延时 实验六:类比多智能体系统,为了达成一致,网络中的每个节点必须通过连接将其状态信息传递给相邻节点。由于信息和物理环境的限制,连接节点之间的通信约束是不可避免的,其中通信延时是最普遍的通信约束之一。本实验分别设置不同通信延时对系统进行仿真,各发电机转子动态响应曲线如图10所示。可以看出,在不同容量限制的条件下,本文所设计控制器相对文献[21]中的控制方法,能够在储能系统容量较低的情况下,更加有效地对抗时延干扰。 图10 不同通信延时下系统稳定时间 针对网络物理智能电网的暂态稳定性问题,提出了一种新型的非线性分布式控制设计方法,并通过MATLAB-Simulink仿真平台验证了所设计控制器的性能。该控制器对实时测量中的延迟等网络干扰具有良好的抗扰能力,可以为未来的信息物理系统提供暂态稳定解决方案。此外,虽然目前为支持将可再生能源纳入电网而部署的DSS技术成本较高,但提高电力系统暂态稳定裕度会增加它们向电网提供的服务价值。因此,本文方法可令安装更多测量系统在经济上可行,且有助提升电网消纳可再生能源的能力。为了进行比较研究,在实际的限制条件下,对最新开发的基于PFL的控制器进行了仿真。仿真结果表明,在相同的实际限制条件下,该控制器具有较好的暂态稳定性能。 本文在考虑电网实际运行中的通信延时问题时,基于不同发电机之间具有相同延迟时间的条件下,设计了分布式稳定控制器,但是电网中存在不同通信延时的情况,此时控制理论证明并不适用。未来将研究电网具有不同通信延时的暂态稳定问题。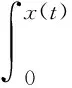
1.2 电力CPS系统模型
2 分布式控制器的设计

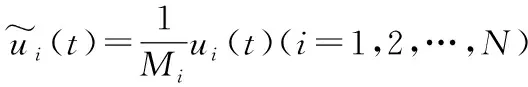

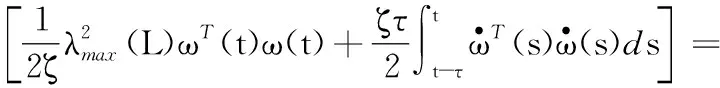
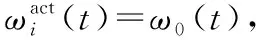
3 仿真分析

3.1 系统物理网络故障
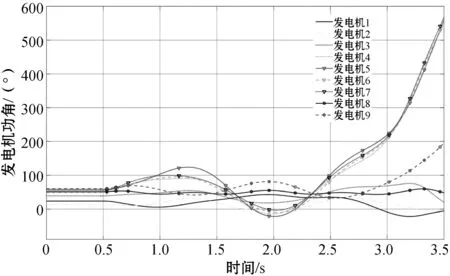
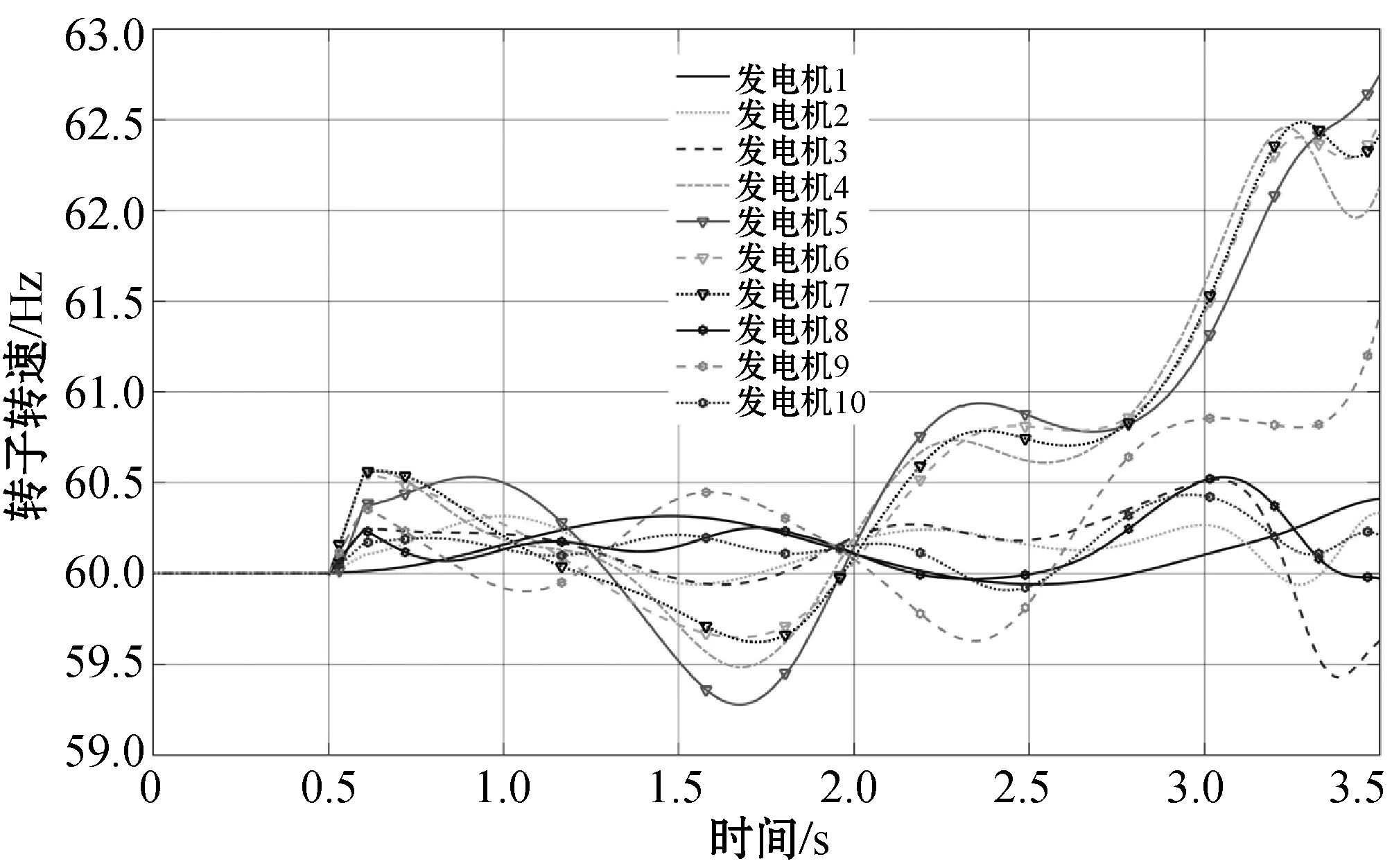
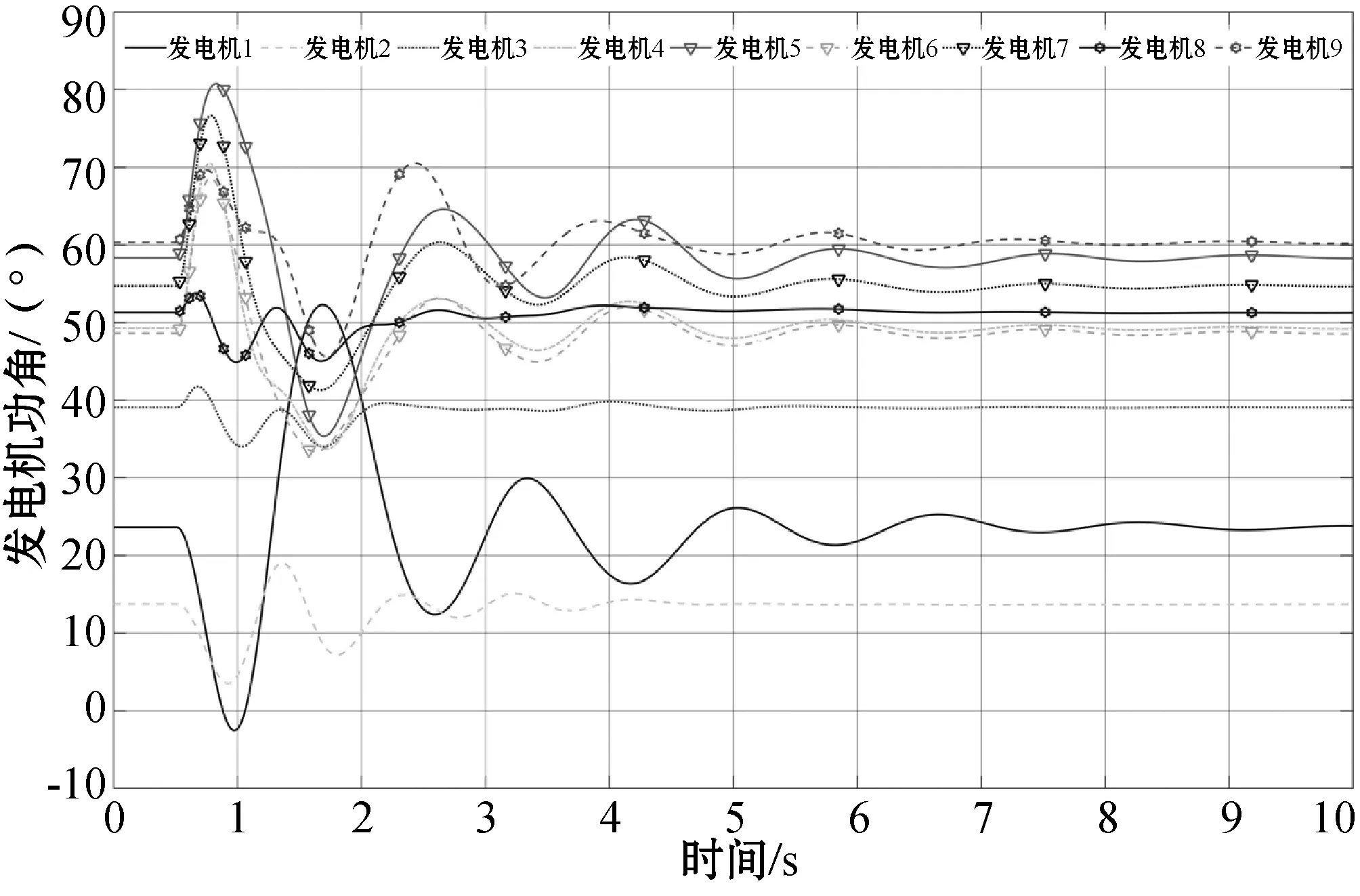
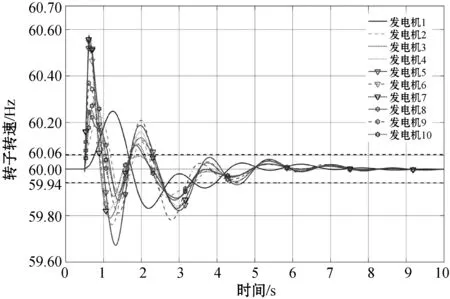
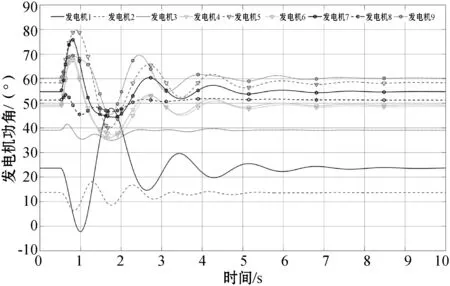
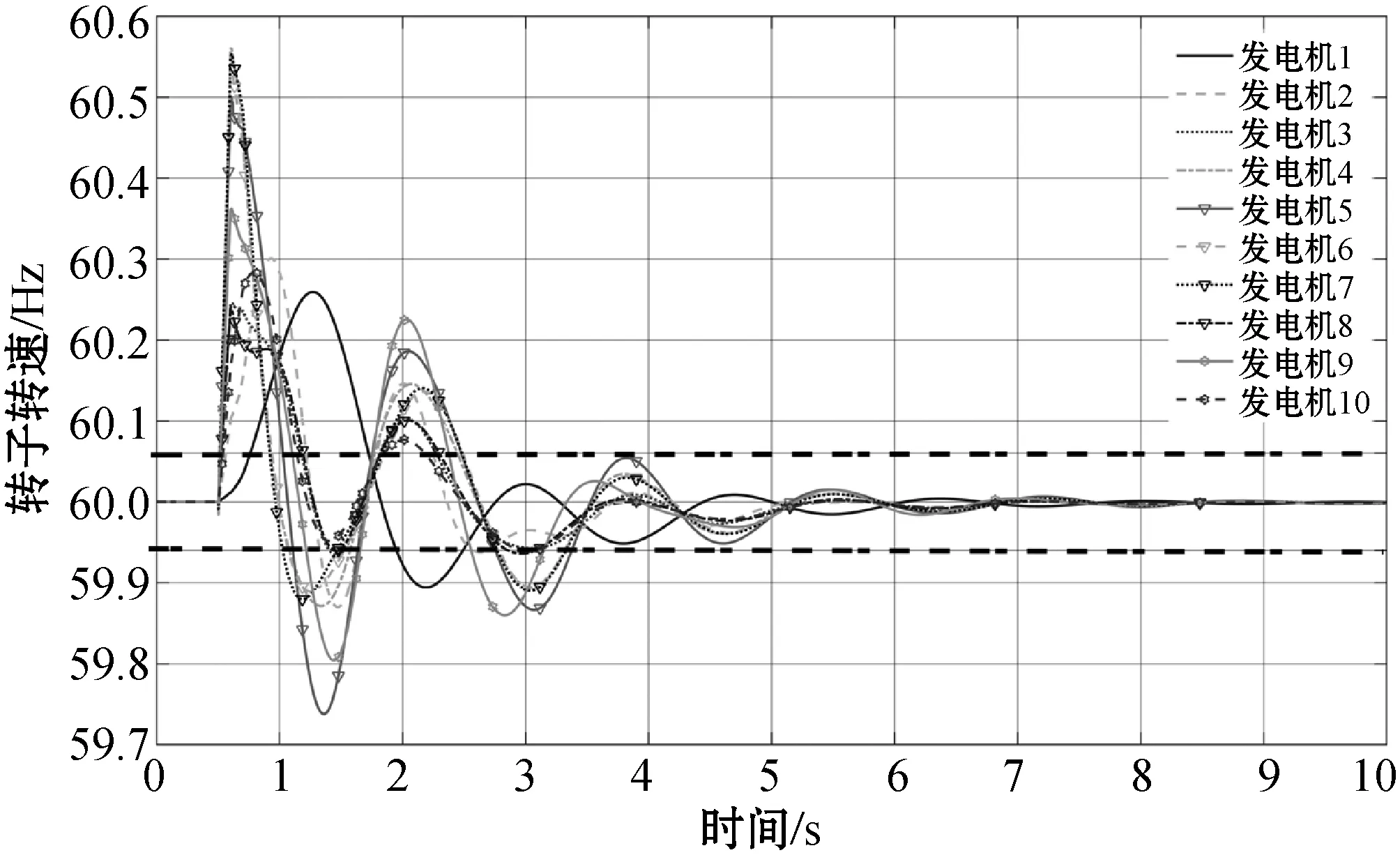
3.2 考虑电网实际限制条件
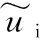

4 结 语

