测量数据中色噪声处理方法探讨

付 莉，高 冰，刘明波

（中国人民解放军91388 部队，湛江 524022）

1 引 言

采用经纬仪进行测量的过程中，测量数据y（t）由真实信号Y（t）、系统误差s（t）和随机误差e（t）组成，即y（t） ＝Y（t） ＋s（t） ＋e（t）。 系统误差影响测量结果的准确度，随机误差影响测量结果的精密度。 要获得高精度试验处理结果，必须准确地分离测量数据中的系统误差和随机误差。

经纬仪测量数据中的系统误差主要是指定向、零位、轴系、跟踪部位等具有常值或有规律的误差，在明确系统误差模型的条件下，可以精确地予以修正。

目前，对测量序列随机误差影响的消除主要采用平滑滤波的方法，如中心平滑、多项式拟合等。平滑处理后数据的误差有所降低，但由于平滑处理模型使平稳时间序列的点与点之间相关（时序相关），若使用的数据要求采样率较高时，如要求数据处理步长为40 fps 点或更高时，就出现了数据时序相关问题。

本文针对目前经纬仪测量数据在高采样率下随机误差具有较强相关性的实际问题，对数据的相关步长判别方法和相关数据的处理策略进行了分析探讨。

2 白噪声多项式平滑方法

在讨论相关数据平滑处理前，首先介绍目前测量数据中的随机误差为白噪声时，所采用的正交多项式平滑方法，作为相关数据平滑处理的基础。

设测量数据为｛y，y，y，……，y｝

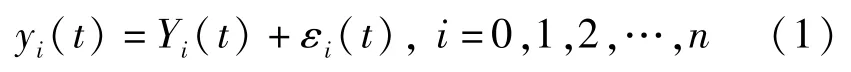
式 中： y（t）——观测数据； Y（ t）——真 值；ε（t）——平稳噪声。

当随机误差为白噪声时，E［ε（t）］ ＝0，D［ε（t）ε（t）］ ＝σ，σ为噪声方差。

为便于计算及统计分析，采用切比雪夫正交多项式的线性组合来逼近y（t），即

其中，φ（t）是切比雪夫正交多项式。

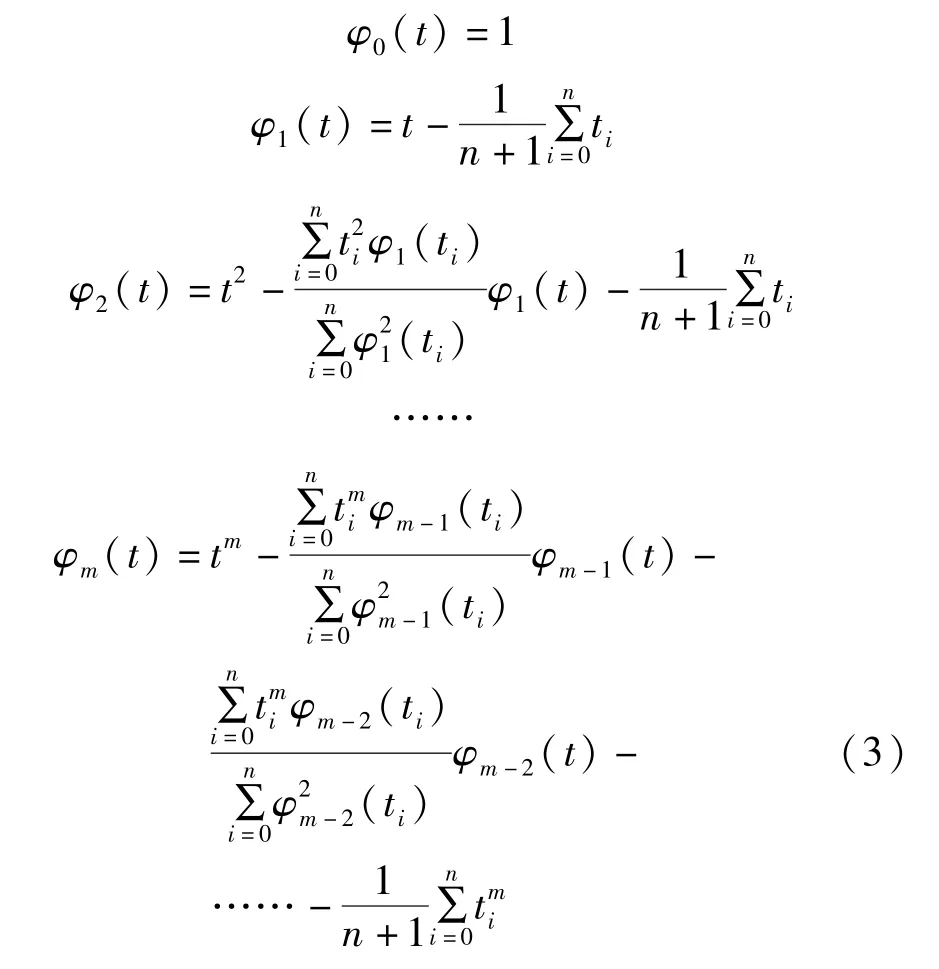
当k ＝l 时，切比雪夫正交多项式满足以下条件

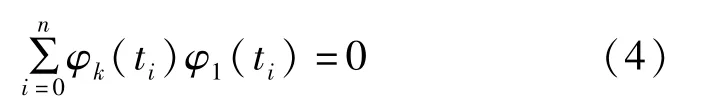
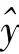
其中，b（k ＝0，1，……，m）为待估系数。 令Q ＝min，利用φ（t）的正交性，得b的最小二乘解为

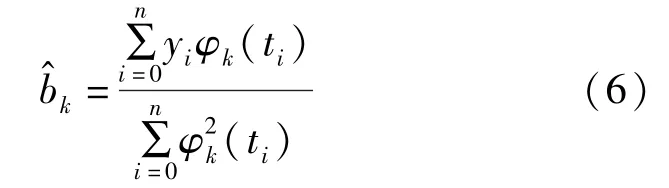
这就是目前普遍采用的正交多项式平滑处理方法。

3 非相关转化法

采用差分的方法检验数据的相关性，导出相关条件下差分步长的计算方法，通过求取测量数据的不相关步长，将具有相关特性的原始测量序列转化为若干个不相关的数据序列。

3．1 测量数据的差分方法

设测量结果为y，y，……，y，则一阶差分为

（y－ y），（y－ y），……，（y－ y），……，（y－y）；

二阶差分为

（y－y） －（y－y） ＝（y－2y＋y），（y－2y＋y），……，（y－2y＋y），……，（y－2y＋y）；

……

因为t是等时间间隔分布的，当做P 阶差分时，凡包含有系数的各项均为0，剩下的是包含随机误差的项，所以根据一组P 阶差分的值可以算出随机误差的估计量。 差分也可以每隔若干个数据相减，例如：

（y－ y），（y－ y），……，（y－y）

间隔的长度L 称为差分步长。

3．2 不相关步长判别方法

按照上面介绍的差分方法，对原始测量数据序列y做P 阶向前差分处理，得到一组新的数据序列

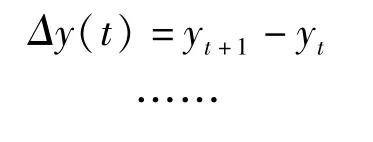
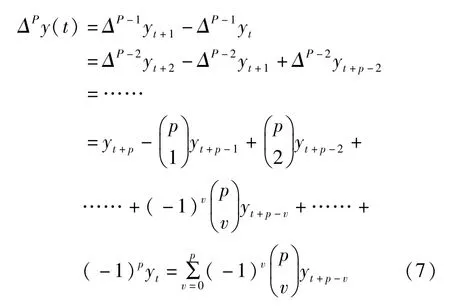
根据P 阶差分序列计算随机误差的统计方差S为

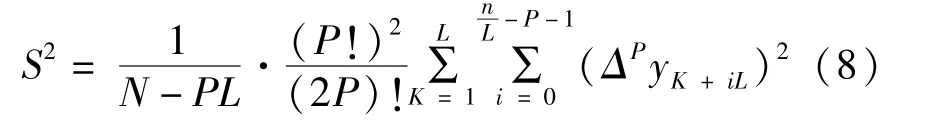
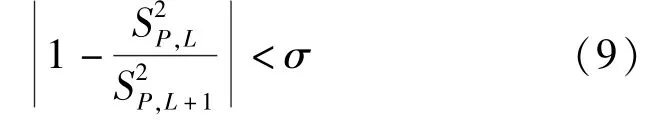
不成立，说明步长L 偏小，应增加为L ＋1；如果公式（9）成立，则认为步长L 是合适的，即测量数据是不相关的，此时L 为最小不相关步长。 其中，σ 为一个根据需要确定的小正数，一般取σ ＝0.05。

3．3 非相关处理策略

在计算得到L 后，可采用下面的方法对测量数据进行平滑处理。

3．3．1 序列重组

将原测量序列按照不相关步长拆分成L 个不相关测量数据序列，此时，各序列的数据点为原序列中以L 为间隔的采样点，并满足不相关条件。

如原始测量数据序列为

y，y，y，……，y，y，y

由第3.2 条中的方法计算得到L ＝4，则可将原始测量序列拆分成4 列不相关数据序列

3．3．2 平滑滤波处理

对得到的各个不相关序列可采用目前普遍采用的白噪声数据平滑滤波方法，如中心平滑滤波、端点平滑滤波、多项式拟合平滑滤波等方法。 具体方法不再赘述。

3．3．3 序列还原

将平滑滤波处理后的各序列，按照时间顺序重新恢复成以测量采样间隔为步长的完整序列，得到

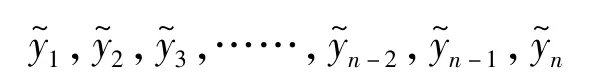
即经过非相关转化法处理得到的平滑结果。

3．4 随机误差的统计结果

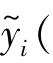
对随机误差序列采用贝塞尔公式统计为

3．5 实测数据计算分析

以某红外测量设备为例，使用该设备对某空中飞行目标进行测量，受周围气候环境影响以及目标形状和姿态等变化，导致测量数据随机误差严重超差。 经分析，此情况下获取的测量数据含有较强噪声，不满足理想情况下对该型设备的鉴定结果，同时，原来白噪声前提下的数据处理方法和模型也不再适用。

采用前面提出的相关数据分析处理方法，对该次测量数据进行分析；在获取不相关步长后，将该测量序列拆分成多个不相关数据序列；再对各不相关序列按照白噪声处理方法进行处理，并将处理后的各序列重组，获取目标空中飞行轨道。两种情况下的测量数据序列处理结果误差比对如图1 所示。

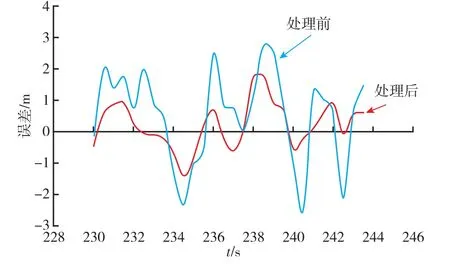
图1 处理结果误差比对Fig．1 Error comparison of processing results

4 相关数据平滑法

探讨从另一个角度对具有相关性的测量数据进行平滑的方法，即不考虑测量数据是否相关，将前面介绍的利用正交多项式对白噪声测量数据进行平滑的方法，推广到随机误差相关时的情况。

4．1 相关系数计算方法

将公式（6）写成向量形式为

其中，

由φ（t）的正交性有

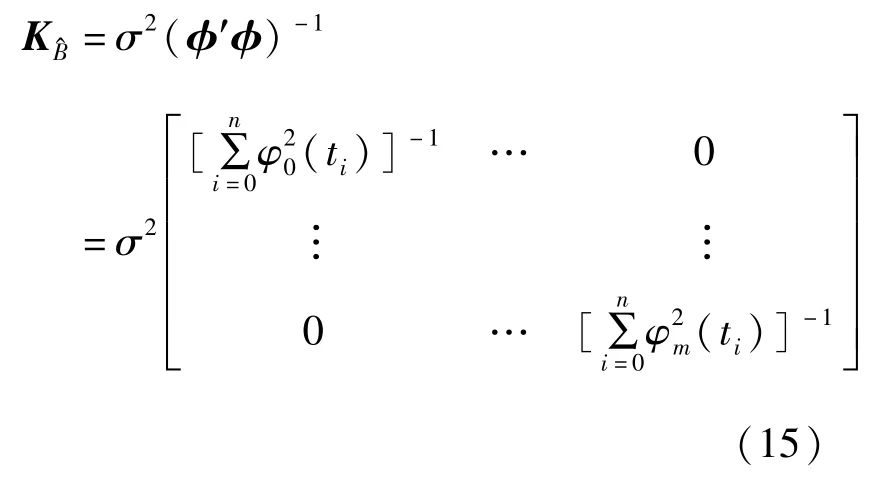
即

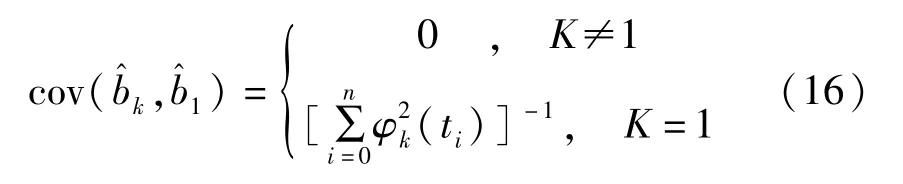
其中，

（K，1 ＝0，1，……，m）

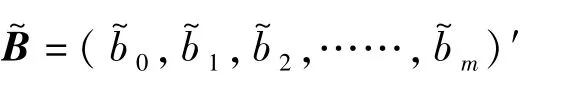
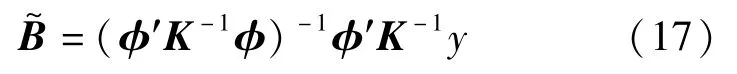
4．2 相关测量数据平滑处理方法

对离散测量数据进行平滑的方法，在考虑测量误差的相关性时，要比白噪声数据的处理复杂得多，关键是求出误差相关矩阵的逆。 但在实际工作中要精确给出一个观测序列噪声的相关矩阵并不是很容易，再加上矩阵求逆往往比较复杂，这就给滤波器的设计带来了困难。 为了较准确地描述和分析测量中相关噪声的性质和影响，现采用简单广义马尔可夫噪声作为相关噪声的一阶近似。

具有标准化自相关函数的广义平稳连续随机过程称为简单广义马尔可夫过程。

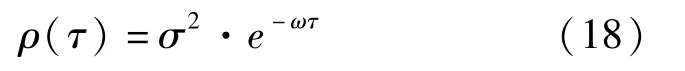
其中，ω ＞0 称为噪声带宽，可由实验确定，它的大小反映了相关性的强弱。 ω 越大，相关性越弱。

基于上述理由，为了简化分析与计算，现假设测量随机误差为平稳过程，则有零值数学期望和由公式（18）定义的自相关噪声。

在这种情况下，误差相关矩阵K 的逆矩阵K是对称三角阵

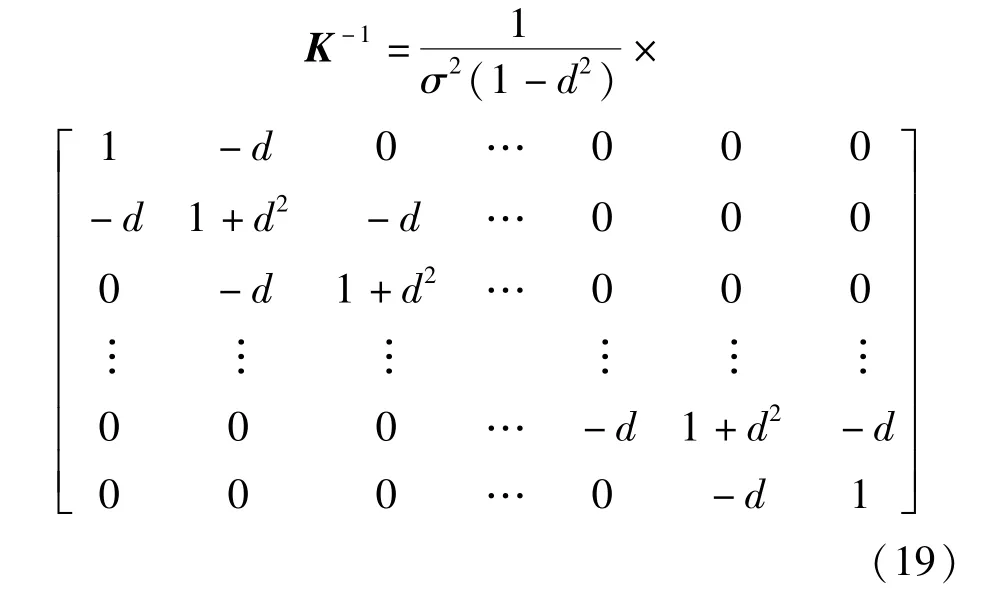
其中，

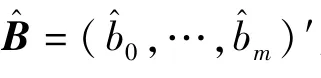
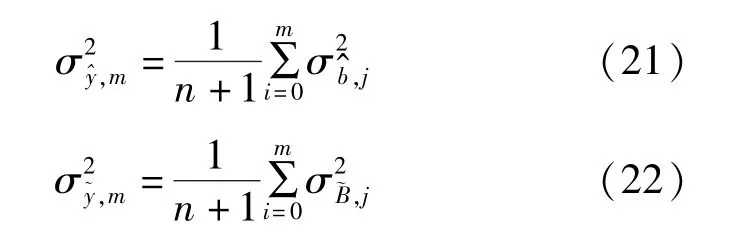
当n→∞时，上述两种估值的方差均趋于同一极限（与m 无关），则

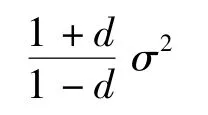
当d ＝0 时，两种估值意义相同，有

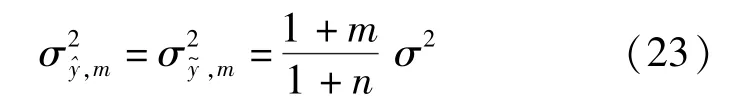
这实际上是测量误差非相关时的平滑值方差。

当d≠0 时，平滑值的方差总是超过非相关情况下的相应方差值，在自相关函数可用简单广义马尔可夫过程描述的情况下，不考虑测量误差相关性所造成的平滑值方差增加是很小的，这时可按测量误差对白噪声进行处理，而不至于使误差增加很多。

5 结束语

随着技术发展，经纬仪测量数据的录取频率越来越高，从过去要求的1 fps、2 fps，提高到10 fps、20 fps，甚至更高。 因处理频率的提高，数据的相关性明显增强。 特别是随着多传感器测量设备的研制和在实际测量中的应用，因其测量手段的多样化和测量工程原理与背景环境的复杂性，提供用于处理的信息已远远超出过去传统意义上的误差简化为白噪声的情况。 原有数据处理方法假定测量数据是白噪声的前提条件已不满足。

本文针对因现有测量条件的变化和数据处理要求的提高所带来的新问题进行了分析和探讨。通过采取适当的处理策略，拓宽了原有数据处理方法的应用领域，增强了数据处理系统的适应能力。