容量受限下城市对航班四维航迹优化

谢华，黎子弘,*，杨磊，朱永文，刘芳子,3

1. 南京航空航天大学 民航学院，南京 211106 2. 国家空域技术重点实验室，北京 100085 3. 中国民用航空局 空中交通管理局 战略发展部，北京 100020

面向航空运输需求持续增长态势，如何在维持空中交通运行安全和高效的同时，提升航班燃油效率，改善航空运输环境影响，是全球航空运输系统转型发展的关键目标和重要挑战之一。革新航空制造技术、改善航空运输相关的社会经济学政策、优化航班运行过程以及寻找替代燃料4个方面是提高燃油效率的途径。根据国际民航组织航空环境保护委员会(Committee on Aviation Environment Protection, CAEP)估计，通过改善航空管理框架，优化空中交通运行，从2015—2025年每年可减少燃油5.4～10.7 Mt。欧洲单一天空计划(Single European Sky ATM Research, SESAR)、美国下一代航空运输系统(Next Generation Transportation System, NextGen)、中国民航空管现代化战略(Civil Aviation ATM Modernization Strategy, CAAMS)均对未来空中交通运行赋予了环境友好、可持续发展的新内涵和新使命，并将提升燃油效率列入空中交通管理性能指标体系中。因此，通过航迹优化提高航班的燃油效率已成为各国学者们研究的热点。

基于航迹运行(Trajectory-based Operation, TBO)是新一代航空运输系统的基本特征之一，旨在通过各利益相关方持续的信息交换，实现起飞前和飞行中的四维航迹规划与控制，对于增强空中交通可预测性和飞行效率具有重大作用，也为航班提高燃油效率提供了新手段。目前，以提升燃油效率为目标的航迹优化根据航班运行阶段进行划分，包括爬升、巡航和下降3个阶段。

当航班爬升、下降时，研究更多聚焦于航班最优垂直飞行剖面的设计与评估，即连续爬升运行(Continous Climbing Operation, CCO)和连续下降运行(Continous Descending Operation, CDO)。作为提高终端区航班运行效率和经济效益的关键技术，CCO和CDO能够有效地减少噪声影响、油耗和废气排放，引起了各国学者和业界的关注。随着研究和试点的不断深入，传统终端区标准进离场程序较为刚性，难以支撑TBO下最优航迹规划与实施的问题愈发凸显。文献[15-17]通过重构终端区空域结构与运行模式，支撑终端区四维航迹安全高效运行，促进了CCO和CDO的实际运用。

航班在巡航阶段时主要考虑油耗、排放和凝结尾及对气候的影响。针对垂直剖面，Lovegren等通过改善高度与速度剖面提高航班的燃油效率。Williams等加入欧洲和北美地区的航班巡航高度限制，开展高度层优化分配以降低凝结尾和碳排放；针对水平剖面，王宇等考虑风场和雷雨区，综合经济性和环保性两类目标，在预战术阶段对航班纵向飞行轨迹进行优化。Hartjes等以总油耗最小为目标，研究长途商用飞机飞行编队的整体飞行性能，并分析了风场对飞行编队性能的影响。研究发现，飞行路径的选择对运行性能和环保性能具有显著影响，飞行水平轨迹和垂直剖面的协同优化逐渐成为近年来的研究热点。

然而，上述研究是从航班的燃油效率与环境效率开展的，考虑扇区容流平衡、空域使用限制等因素较少。针对该问题，基于所需到达时间(Required Time of Arrival, RTA)限制的航迹优化是空地航迹协商运行的重要技术，旨在通过限定航班到达关键节点的时间控制空中交通流量，也是新一代空中交通管理系统和飞行管理系统研制中的关键技术之一。在巡航阶段，García-Heras等对比了4种航迹优化方法在RTA下的求解性能，验证了伪谱配置法的有效性。Mendoza等使用ABC算法为航空器规划RTA下的最优垂直剖面。在终端区，Gu等针对下降阶段，从燃油经济性、温室效应和飞行速度变化3个方面开展研究，并采用遗传算法规划不同情况下航空器的最优飞行剖面。Dalmau等研究了RTA下的连续下降轨迹，认为RTA下的CDO可以在不影响机场容量的情况下，减少航空器的噪声、排放和燃油消耗。

航迹优化当前的研究重点主要聚焦滑行、起飞、巡航和着陆等不同飞行阶段的四维航迹优化技术，在战略和预战术层面提出了诸多航迹规划方法，但仍存在以下局限和触及较少的领域。① 航 迹规划更多针对飞行阶段单独优化，跑道到跑道，甚至“门到门”的完整航迹优化探讨较少，航迹优化更多集中在横向路径或垂直剖面单一维度；② 航迹优化过程中对于航路航线候选空间和容流平衡关系等现实约束考虑较少；③ 空域拥堵的时空特征对于航迹优化结果影响的探讨鲜见。鉴于此，本文在已有研究成果基础上，以上海虹桥—北京首都为例，提出了容量约束下城市对航班四维航迹优化方法，研究面向战略阶段的航迹优化问题，综合考虑航空器动力学性能限制、可用航路限制、扇区容量约束、空中交通管制对于航班运行高度和速度的限制等，建立了“跑道-跑道”航迹多目标规划模型，为航班规划在空域资源受限时的航迹，以期科学配置空域资源，切实提升航班的燃油效率，在一定程度上促进TBO的应用实践。

本文的主要工作包括：

1) 建立了“跑道-跑道”四维航迹模型和燃油消耗模型，针对起飞后扇区容流关系变更所造成的航班可用进入时隙调整，建立结构性空域内基于可用飞行路径集的四维航迹多目标优化模型，设计带精英策略的非支配排序遗传算法(Non-dominated Sort Genetic Algorithm-Ⅱ, NSGA-Ⅱ)对模型快速求解，探究空域容量受限时，油耗与飞行时间权衡关系下，协同优化城市对之间的飞行路径和飞行剖面。

2) 考虑单一扇区容量受限，通过设计不同扇区、不同拥堵程度的交通场景，分析扇区进入时间偏移量、受限扇区距离起飞机场的距离与优化结果(Pareto前端解特征)之间的关系，探讨航迹优化结果如何随着空域拥堵的位置和严重性的变化而改变。

1 问题描述

起飞前，航空公司可以根据气象条件、计划航程时间、计划航路和预计起飞重量等信息，规划经济飞行剖面。然而，现实运行中受空域可用性、容流平衡管理和管制指挥等外部动态因素扰动，经济航迹往往难以执行。如何规划在扇区容量受限情况下的飞行路径与飞行剖面，是本文所要解决的主要问题。针对该问题，本文权衡油耗和飞行时间，构建了可选路径下考虑扇区控制到达时间(Controlled Time of Arrival, CTA)约束的城市对航迹优化模型，为简化问题，以1 km为单位对航班的水平轨迹进行离散化处理，将时间连续航迹优化问题转化混合整数非线性规划问题(Mixed-Integer Nonlinear Program, MINLP)，从而得到有限的决策变量集合。

本文将固定结构航路抽象为一个网络=(,)。其中，={,,…,}为节点集合，表示每个航段起点的序号，={,,…,}为航段集合，航段长度设为1 km。设前后两个节点分别为和+1，构造邻接矩阵=[,+1]，设若→+1连通时，[,+1]=1，否则[,+1]=+∞。此时航班的路径可表示为一系列连通节点的集合。那么，本问题可以表述为：在网络内连通性约束下，综合各类运行限制，根据受限扇区的可用时间窗，规划航空器飞行高度和速度剖面，权衡优化油耗和飞行时间。其中，飞行油耗根据第2节中的航空器动力学模型、航空器性能模型和第3节航空器油耗模型得到。本文的四维航迹优化框架如图1所示。其中，BADA PTF文件中推荐的航班爬升率/下降率见文献[31]。

图1 四维航迹优化框架Fig.1 Four dimensional trajectory optimization framework

2 航空器四维航迹建模

2.1 大气模型

为了使模型更接近航空器的真实运行环境，本文使用Eurocontrol出版的BADA 3.11中的大气模型来模拟大气的温度、密度和气压随高度变化的情况，如式(1)～式(3)所示:

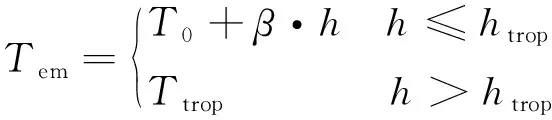
(1)

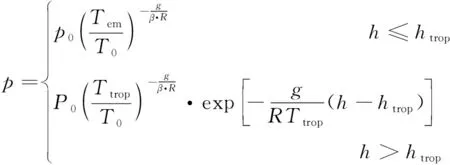
(2)

=

(3)

式中：为大气温度；为对流层顶温度；为对应高度下的大气压强；=101 325 Pa为平均海平面标准气压；=28815 K为平均海平面标准大气温度；=11 000 m为对流层顶高度，在对流层以上温度是恒定值；=-0006 5 K/m为对流层顶以下温度变化梯度；=287052 87 m/(K·S)为空气气体常数；=98 m/s为重力加速度；为大气密度。

2.2 航空器动力学模型

为准确评估航空器的燃油消耗和飞行时间，本文根据点质量模型(Point Mass Model，PMM)与全能量模型(Total-Energy Model，TEM)并根据问题进行适应性改进，建立动力学模型模拟航空器飞行。

根据PMM，假设所有的力都作用在航空器的重心上，航空器的运动减少到3个自由度(3个平动)，3个平动的导数方程可以沿时间积分。作用在航空器上的力如图2所示。图2中：为航迹角；为飞行迎角；为发动机安装角，通常很小，近似认为=0°；为航空器受到的重力；为真空速(Ture Air Speed, TAS)；为升力，为航空器受到的阻力，通常表示为

(4)

(5)

式中：为参考机翼面积；和分别为升力系数和阻力系数，计算公式为

(6)

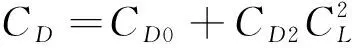
(7)

式中：为航空器的坡度；0为寄生阻力系数；2为诱导阻力系数。

在不考虑风的分量的大气参考系中，航空器运行过程中的相关飞行参数计算式为

图2 作用在航空器上的力Fig.2 Force acting on aircraft

(8)

式中：为沿着飞行路径的距离；为燃油流率。令状态向量=[,,,]，控制变量=[,]。在本文中，依照航程对于水平轨迹离散化后，为了便于计算，在航段→+1中，航空器的、以及爬升/下降率(Rate of Climb or Decent, ROCD)保持不变。

根据TEM，作用在飞机上的力所做的功的比率等于势能和动能的增长率，即

(9)

2.3 航空器性能模型

飞机性能是描述飞机质心运动规律的参数，包括速度、高度、推力等。本文使用的飞机性能模型和参数均来自BADA 3.11。

在模拟航空器运动的过程中，推力的获取至关重要。本文将推力的计算转化为对加速度的求解，即当ROCD,+1、确定后，根据式(10)，即可推定航空器在航段→+1的加速度，结合式(9)即可计算航空器在→+1的推力,+1。

(10)

式中：为航段→+1的距离；,+1为航段→+1的飞行时间。不同飞行高度对应的可行ROCD,+1根据BADA的PTF文件确定。

航空器的速度也是飞机性能的重要参数。根据BADA 3.11的OPF文件，校正空速(Calibrated Air Speed, CAS)可以判断航空器是否失速。CAS与TAS之间的关系为

=

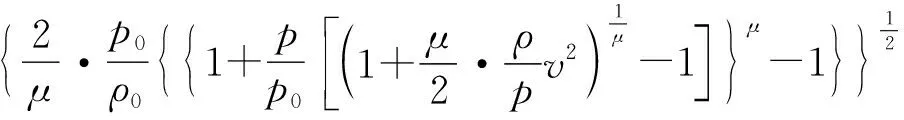
(11)

(12)

式中：=1225 kg/m为标准海平面的大气密度值；=14为空气比热容比。

将式(1)～式(12)记为性能方程组。当航空器飞行至初始节点，飞行路径、状态变量及控制向量确定后，航空器依据BADA 3.11中PTF文件推荐的ROCD所得到的加速度进行控制，即可推定飞行过程中航空器在任意节点的状态向量及控制变量。

3 航空器油耗模型

在计算油耗时，本文采用BADA 3.11的燃油流率模型并进行适应性改进，计算航空器从起飞至着陆阶段的燃油消耗。根据BADA性能模型，对于喷气式飞机：

(13)

式中：为推力比燃油消耗；为第一推力比燃油消耗系数；为第二推力比燃油消耗系数；航空器的燃油消耗为燃油流率在整个飞行时段内的积分。

在本文中，依照航程对于水平轨迹离散化后，航空器飞行油耗可近似为从初始节点到终止节点整个航迹上每一航段的油耗离散值之和，计算公式如下：

(14)

由式(13)可知，要计算油耗必须先得到航空器的推力。当已知航空器在任意航段→+1的高度和速度，即、、+1和+1，首先根据式(15)推定航空器在航段内的加速度，接着结合式(9)即可推定航空器在航段内的推力,+1。

(15)

除了巡航阶段和慢车推力，式(14)都适用。本文不考虑慢车推力的情况，故巡航阶段的燃油流率f如式(16)所示。

=··

(16)

式中：为巡航燃油流率因子。

4 航班四维航迹优化建模

为简化问题，作如下基本假设：① 采用航空器的光洁构型进行优化；② 忽略风对航班飞行的影响。

4.1 决策变量

(17)

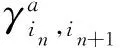
(18)

式中:[,+1]=1。

4.2 目标函数

在TBO中，协同流量管理系统(Collaborative Decision Making, CDM)能够通过融合各类空地限制为航班分配起飞时刻。然而，由于起飞时隙锁定具有提前量，且空中交通运行具有不确定性，可能发生扇区容流关系变化导致航班原定扇区进入时隙不可用。在基于航迹运行中，航班在空地协商环境下重新规划飞行航迹，以满足受限扇区的可用进入时间窗要求。因此，该模型旨在根据飞行性能，以预先设定的水平路径为基础，在满足基本空中交通运行限制下，允许航班根据起飞后扇区容流关系更新自主选择飞行路径，实现航班水平轨迹、垂直剖面和飞行速度的一体化规划，优化飞行时间和燃油消耗，如式(19)所示：

(19)

4.3 约束条件

1) 连通性约束

航班所选的路径中的相邻节点必须在网络中相连。

(20)

2) 唯一性约束

航班经过任意一点后的下一节点有且仅有一个。

(21)

3) 高度约束

航班在飞行过程中需要满足高度限制约束。该限制由航班自身性能和空域高度限制共同决定，如式(22)所示。

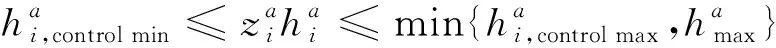
(22)

特别地，在航路飞行阶段，若为双向航路，航班除满足上述约束外，还应遵循“东单西双”规定，即往东飞的航班采用单数高度层，往西飞的航班采用双数高度层的限制。

∀∈，∈{0,1,2,……}

(23)

4) 速度约束

航班在节点的速度必须同时满足自身性能和扇区管制规则的限制。

(24)

特别地，加速度是一个与航班性能相关的值，影响着航班安全运行所需的推力，对于加速度的约束，也在间接约束了航班运行所需的推力。考虑到旅客舒适度，加速度不能过大。

(25)

5) 爬升下降性能约束

航班的爬升率和下降率不能超过最大爬升率和最大下降率。

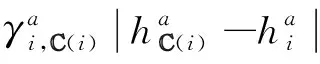
(26)

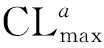
(27)

(28)

6) 扇区容量约束

航班进入受限扇区的时隙必须为扇区的可用时隙。

(29)

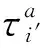
7) 时效性约束

时间效益是航空公司效益的另一个重要维度。因此，在规划经济航迹时，应考虑城市对空中飞行时间在一个可接受范围内，如式(30)所示。

(30)

式中：STF为航班的标准空中飞行时间(Standard Airborne Time of Flight, SATF)，根据飞机计划和CDM系统得到；MAD为正数，表示航班最大可接受延误(Maximum Acceptable Delay, MAD)；MAA为负数，表示航班最大可接受提前量(Maximum Acceptable Advance, MAA)。

5 算法设计

航班航迹优化问题的复杂度随决策变量数量的增多以几何级数增长，且决策变量之间存在强烈的耦合关系，难以在多项式时间内得到和验证解，故而采用元启发式算法进行求解。遗传算法(Genetic Algorithm, GA)是一种通过简化自然界生物的遗传过程来实现对复杂空间的启发式搜索的数学方法，该方法可以推广到多目标优化问题中。带精英策略的非支配排序遗传算法(Non-dominated Sort Genetic Algorithm-Ⅱ, NSGA-Ⅱ)是解决多目标优化问题经典算法，其引入精英策略，提出了快速非支配排序法和拥挤度比较算子，不需要预先指定共享参数，近年来已被大量运用于优化问题。研究表明，NSGA-Ⅱ在求解质量、收敛效率方面具有综合优势，故本文采用该算法对所建模型进行求解，算法流程如图3所示。图中，F1、F2、F3表示染色体。本文对算法的编码与解码、初始种群和交叉变异算子进行适应性改进；同时针对交叉、变异产生不可行染色体的情况，设置了修正算子，具体内容如下。

图3 NSGA-II流程图Fig.3 NSGA-II algorithm flowchart

1) 编码与解码

为了提高算法的运算效率，本文设计了分层可变长度染色体，如图4所示。第1层为基于决策变量,+1的0～1矩阵，表示航班选择的路径。绿色的基因表示根据邻接矩阵=[,+1]，节点与+1之间具备连通性。否则，节点之间不具备连通性，基因被编码为0，在后续的遗传操作中不会被改变。第2层采用整数编码，表示从初始节点到终止节点每一节点的高度和速度。需要注意的是，第2层的长度由第1层中编码的飞行路径决定。

图4 染色体编码方式Fig.4 Chromosome encoding pattern

2) 初始种群

初始种群作为启发式算法的迭代起点，是影响种群进化结果和算法效率的重要因素。本文将历史航迹数据作为初始解，形成初始种群进行航迹优化。需要注意的是，航班的高度和速度对机动动作、气动构型变化和气象条件等因素具有显著敏感性。因此，为求解经济垂直剖面和速度剖面，本文对最为初始解的历史航迹数据中的高度和速度数据作平滑处理。

3) 交叉算子

本文采用交叉算子产生新的水平路径。为了提高搜索效率，本文设计了两种概率相同的交叉算子:① 路径交叉导致高度和速度剖面同时交叉；② 选择路径相同的染色体进行高度和速度剖面交叉。需要注意的是，在实际的空中交通系统中，航路网络中的分叉节点数量是有限的。因此，针对第一种交叉算子，为了提高运算效率且保证交叉后节点仍然连通，交叉节点根据第一层染色体从航路网络的分叉节点中随机选择。

4) 变异算子

速度剖面寻优。当变异节点确定后，根据变异位置的不同，采用不同的变异方式。

(31)

当航班处于巡航阶段，处的高度与速度分别根据式(32)以相同的概率进行扰动。

(32)

5) 修正算子

由于前序节点对后序节点有较大影响，染色体进行交叉、变异操作后必须验证其可行性。若满足约束条件，则获得子代染色体，否则根据以下方式对染色体进行修正。

本文以高度剖面为例说明修正算子。如图5所示，为交叉节点，为变异节点，航班在交叉节点和变异节点的高度和速度分别为、、m和m，变异节点的蓝色实线是原始垂直剖面，红色实线是交叉或变异后的垂直剖面，显然航班无法在相邻节点间完成高度的剧烈变化。针对交叉造成染色体不可行的修正方式如图5(a)所示，其中，c+1与c+1分别为航班在节点+1处的速度与高度。需要说明的是，航空器在节点+1及后序节点的高度与速度信息来自另一条染色体。首先，比较与+1的相关关系。如果<+1，=+1或>+1，则假设航班以为起点，分别作加速爬升，等速爬升和减速爬升，根据性能方程组以及BADA推荐的爬升率计算并修正航班在后继节点的高度和速度，直到航班在某一节点处k=+1且k=+1时修正结束。该修正算子对于变异产生的高度骤降也同样适用。

针对变异造成染色体不可行的修正方式如图5(b)和图5(c)所示。首先，基于原始垂直剖面，判断在变异节点后是否存在阶梯爬升。若存在，记航班完成阶梯爬升时的节点为，修正过程如图5(b)所示：以为起点开始修正，直到航班在某一节点处k=l且k=l，修正方式与交叉修正算子一致(见图5(a))，不再赘述。随后，航班在航段→保持匀速平飞，修正结束。该修正算子对于航班在节点后存在阶梯下降也同样适用。

图5 修正算子示意图Fig.5 Illustration diagram of correction operator

6 实例分析

6.1 基本参数

6.1.1 航路结构与运行限制

本文选择中国最繁忙的航线之一ZSSS-ZBAA作为研究对象，2019年7月1日作为典型日，其航路航线及其所经过扇区如图6所示。需要说明的是，本文关注“跑道-跑道”的四维航迹优化，不考虑航班的机场场面运行细节，故将始发和到达机场视为一个网络节点。为研究容流关系临时变更场景下的燃油消耗问题，引入“热点”(Hotspot)的概念，表征某一时段容流失衡的繁忙区域。结合历史运行繁忙程度，设置Sector5与Sector6作为Hotspot。

图6 ZSSS-ZBAA航路结构示意图Fig.6 Schematic diagram of route structure of ZSSS-ZBAA

4条路径的水平距离分别为1 248 km、1 256 km、1 260 km〈〉和1 268 km，航路点信息如表1所示，ZSSS-ZBAA飞行过程限制条件如表2所示。

表1 ZSSS-ZBAA航路点信息Table 1 Waypoint information of ZSSS-ZBAA

表2 ZSSS-ZBAA飞行过程限制条件Table 2 Restrictions of ZSSS-ZBAA flight process

在实际飞行中，高度层的选择必须考虑飞行过程中过航路点的限制以及管制偏好。典型日该周空客A333的高度剖面如图7所示。显然，在到达TOD之前，航班下降到了一个比较低的高度，并保持一段距离的平飞。该周空客A333的巡航高度层与TOD前的平飞高度层如表3所示。在巡航高度层中，10.4 km及以上占比为80.9%，考虑到优化的最终目标是提高航班的燃油效率，初始种群的巡航高度层设置为10.4 km 及以上；在TOD前平飞高度层中，8.4 km和9.2 km占比达到了98.3%，因此选择8.4 km和9.2 km作为TOD前平飞高度层。

图7 典型日该周空客A333飞行高度剖面Fig.7 Altitude profile of A333 of typical day of week

表3 典型日该周空客A333飞行高度层选择Table 3 A333 flight level selection of typical day of week

本文从历史数据中提取扇区容流关系，典型日当天上海虹桥-首都北京所飞经扇区在10:00—14:00 拥挤程度如图8所示。扇区容量为15 min为统计粒度，以5 min为滑动窗口的滚动容量，扇区拥挤程度为流量与容量的比值。

图8 典型日当天上海虹桥-首都北京10∶00—14∶00扇区拥挤程度Fig.8 Congestion in Shanghai Hongqiao Airport-Beijing Capital International Airport from 10∶00—14∶00 of typical day of week

6.1.2 典型机型及其性能参数

根据历史飞行数据，2019年空客A333是ZSSS-ZBAA出现最多的机型，因此选择空客A333作为研究对象，其基本性能参数如表4所示。

表4 空客A333基本参数Table 4 Basic parameters of Airbus A333

6.2 模型校验

为了验证燃油计算模型的准确性，利用QAR数据进行燃油消耗估算。选择上海虹桥-首都北京航班从起飞爬升到下降阶段全过程真实燃油流率值与模型估算值进行对比，如图9所示。可以看出：BADA模型计算所得油耗变化规律与QAR记录数据的趋势基本相同、大小相似。总体上，BADA方法的相对平均偏差为13.7%，拟合度为89.9%，在爬升和平飞阶段燃油流率预测效果较理想，平均相对误差分别为10.5%，8.3%，总体估计精度在可接受范围内。因此，本文所采用的BADA燃油计算模型精度基本满足基于航迹优化的燃油消耗潜力评估要求。

图9 燃油流率真实值与估算值对比Fig.9 Comparison of actual and estimated fuel flow

6.3 算法对比

为验证NSGA-Ⅱ对于容量受限下城市对航班四维航迹规划问题的求解优越性，选取了多目标粒子群算法(Multi-Objective Particle Swarm Optimization, MOPSO)强帕累托进化算法(Improving Strength Pareto Evolutionary Algorithm, SPEA2)2种应用广泛的多目标优化算法，以油耗和飞行时间为优化目标，采用世代距离(Generational Distance, GD)、反世代距离(Inverted Generational Distance, IGD)、最大Pareto前端误差(Maximum Pareto Front Error, MPFE)和超体积(Hypervolume, HV)4类评价指标，如式(33)所示，全面论证算法求解的支配解集与Pareto前沿的逼近程度，其值小越好，而HV则表示算法获得的非支配解集与参照点围成的区域面积，其值越大越好。需要注意的是，在计算下列评价指标时，需对数据进行归一化处理。

(33)

为对比NSGA-Ⅱ、MOPSO和SPEA2这3类算法在该问题下的求解性能特征，选择最短固定路径Route1，以无容量约束下油耗最优航迹为基准设计两种不同的交通场景，即进入Sector5不需要延误和需要延误5 min。ZSSS-ZBAA的SATF为105 min，设定MAA为5 min，MAD为10 min。为增强可对比性，3类算法具有相同的收敛条件： NSGA-Ⅱ和SPEA2的种群数量均为200，最大迭代次数为100，交叉概率为0.9，变异概率为0.1，交叉、变异和修正策略保持一致，变异算子高度扰动值=600 m，变异算子速度扰动值=1 m/s；MOPSO算法中，粒子数目和存档规模均为200，最大迭代次数为100，惯性权重=04，局部速度因子=02，全局速度因子=05。在上述交通场景和基准参数下，3类算法的求解性能如表5所示。

表5 3类算法性能对比Table 5 Performance comparison of three different algorithms

由表5可知，尽管3类算法的求解性能均随着空域拥堵程度的增加而降低，但NSGA-Ⅱ在各类性能指标上都优于其余2类算法。因此，针对本文研究问题，NSGA-Ⅱ能够高效、准确地收敛到Pareto最优解集附近。

6.4 实例验证

NSGA-II算法控制参数设计如下：种群数量为200，最大迭代次数为100，变异概率为0.1，交叉概率为0.9，=600 m，=1 m/s。选择上海虹桥-首都北京典型日10∶00—14∶00这一繁忙时段的4架A333进行实验分析，执行ZSSS-ZBAA的SATF为105 min，设定MAA为5 min，MAD为10 min。实验使用Intel Core i5-6300HQ CPU 2.30 GHz四核处理器，8 GB内存，Windows10操作系统的笔记本电脑，采用Python 3.6.3语言进行编程求解，平均求解时间为216 s。需要注意的是，在不考虑容量约束的情况下，飞行距离对于油耗和飞行时间显然具有绝对性影响，因此以最短路径Route1(无容量约束)油耗最优航迹作为基准，计算航班进入Hotspot的时间，如表6所示。

表6 Hotspot可用时隙Table 6 Available time slots for hotspot

6.4.1 容量受限下的航班四维航迹优化

在容量受限情况下，通过构建不同的邻接矩阵，分别开展容量约束下固定路径和可选路径航迹优化，结果如图10所示，红色直线表示标准飞行时间参考基线。需要说明的，此处的历史飞行油耗是基于本文建立的油耗模型计算所得。为了探究空域拥堵对于优化结果的影响，同时选择最短水平路径Route1(无容量约束)进行优化。结果表明，容量约束对于航班燃油效率具有显著性影响，即考虑容量约束前端解中的任意一个解，都不可能在燃油和飞行时间方面同时优于不考虑容量约束的前端解。同时，容量受限压缩了飞行航迹的权衡优化空间，更为灵活的水平运行空间有助于提升航班燃油效率。与历史航迹相比，固定路径和可选路径航迹优化后的最低燃油消耗平均下降7.91%、6.92%、7.85%、7.26%和8.79%；为了进一步增加对比的现实意义，分别在可选路径和固定路径的Pareto前沿中选择与历史相同或相近的飞行时间(时间平均相对误差分别为0.046%， 0.36%，0.16%和0.12%)所对应的油耗最优解进行对比，固定和可选路径燃油消耗平均下降6.63%、6.48%、6.08%、6.08%和7.71%，验证了路径选择模型的有效性，结果如表7所示。

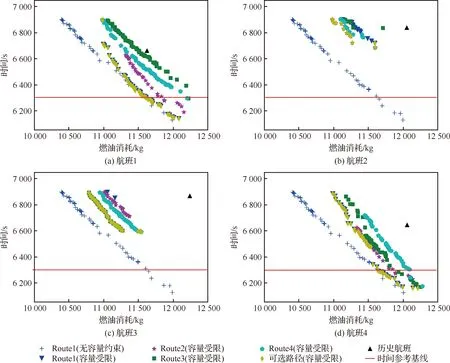
图10 航班固定路径和可选路径的Pareto最优前端Fig.10 Pareto optimal frontiers of floght on fixed and alternative paths

表7 航迹优化结果Table 7 Trajectory optimization results

通常情况下，飞行时间越长，燃油消耗越大，但是实验结果表明油耗与飞行时间存在一定的权衡空间。鉴于此，本文对Route1(不考虑容量约束)飞行过程中的高度、速度参数展开分析。图11为Route1的油耗最优航迹(航班1)与时间最优航迹(航班2)对应的高度和速度剖面与历史飞行航迹的对比图，其中红色实线代表航迹1，蓝色实线代表航迹2，黑色虚线代表典型日空客A333的历史航迹。对比可知，原始航迹中存在较多低高度平飞阶段且巡航过程中高度、速度变化波动较大，造成油耗量增加。航班1和航班2的结果差异显然来自速度的变化。图11中显示，当油耗最小时，航班在264 km处达到爬升顶点(Top of Climb, TOC)，在958 km处达到TOD。巡航高度保持在11 600 m，为了获得最小的油耗，飞行速度下降到197 m/s，为了满足管制偏好，在732 km处下降到8 400 m。当飞行时间最小时，航班在279 km处达到TOC，在958 km处达到TOD，巡航高度保持在11 600 m，巡航速度保持在240 m/s，为了满足管制偏好，在740 km处下降到8,400 m。显然，在满足时效性限制下，高高度低速度巡航可以显著降低油耗。

图11 高度和速度剖面对比Fig.11 Comparison of altitude and speed profiles

需要注意的是，如图10所示，4架航班在hotspot处的计划进入时间与可进入时隙发生的偏离程度不同，航迹优化的结果具有显著差异。其中，航班1和4的优化结果与最短固定路径(Route1)基本一致，表明当计划到达时间略晚于控制到达时间时，航班通过调整速度和高度，保持最短固定路径(Route1)依然可以获得最优性能。特别地，当计划到达时间在一定范围内早于控制到达时间时，如航班2和3，其帕累托前端与固定路径差别甚大。鉴于此，本文根据Pareto前端位置分析其致因因素。

航班2不同路径的Pareto最优前端如图10(b)所示。在容量约束下，燃油效率从高到低依次为Route2、Route4、Route1以及Route3。其原因在于，航班飞越Sector5与Sector6的可用时隙一致且均受限，相较于Route1与Route3，Route2与Route4在进入Hotspot之前就有更长的飞行距离，航班采用较小的速度调整即可满足进入扇区的时隙。加之，Route2的飞行距离相较Route4更短，因此最优Pareto前沿与Route2(带容量约束)Pareto前沿几乎重合。此外，相对于Route1(无容量约束)最优Pareto前沿，所有路径在容量约束下的Pareto前沿权衡空间受到了压缩，飞行时间绝大多数分布在112 min以上。表明在满足航班时效性约束下，采用空中调速推迟航班进入扇区时间的航迹优化空间有限。

航班3不同路径的Pareto最优前端如图10(c)所示。在容量约束下，燃油效率从高到低依次为Route3、Route4、Route2以及Route1。其原因在于，Route3与Route4允许进入Sector6的时隙一致，且Sector6较Sector5的可用时隙更宽松，同时Route3的飞行距离相较Route4更短，因此最优Pareto前沿与Route3(带容量约束)Pareto前沿几乎重合；Route1与Route2进入Sector5的可用时隙一致，但是，Route2在飞越Hotspot之前更长的飞行距离，因此Route2航迹性能优于Route1。特别地，Route1(带容量限制)的最优前沿非常紧缩，相当接近最大飞行时间115 min，运行灵活性较低，说明航班在不具备可选航路空间时，当扇区可用时隙下，通过减速来推迟航班进入Sector5的时间并满足时效性约束这一方式几乎达到了极限，更能体现存在可选航路空间对于提高飞行效率的重要性。

综上，本场景考虑容流管理的动态性，针对起飞后扇区容流关系变更所造成的航班控制到达时间调整，验证了本文所提出的航迹优化方法能够通过同时优化高度、速度和路径选择，权衡飞行时间与燃油消耗，为航班生成满足DCB和CTA限制的四维航迹，探讨了空域拥堵情况下，水平航迹灵活性对于燃油效率的提升作用。

6.4.2 空域拥堵时空特征对优化结果的影响

除了风、温度等高动态大气环境外，现实运行中的航班性能主要受容流平衡管理不确定性影响。鉴于此，本文以固定路径Route1时间最优航迹(不考虑容量约束)为基准，通过改变拥堵扇区的空间位置、拥堵扇区可用时隙与航班计划到达时间的偏移量，探究空域拥堵的时空特征对于航迹优化结果的影响。需要注意的是，为了精细化分析时间偏移量对于优化结果的影响，将滑动时间窗口大小改为2 min进行实验。

在上述场景下，开展不同扇区、不同空域拥堵程度下的航迹优化，结果如图12、图13所示。其中扇区1～扇区7表示Route1依次经过的扇区(依次经过Sector2，Sector3，Sector4，Sector5，Sector7，Sector8和Sector9)，2～12 min表示固定路径Route1时间最优航迹(不考虑容量约束)进入拥堵扇区的计划时间与可用时隙偏移量。总体上，拥堵扇区距离起飞机场的距离与时间偏移量对于优化结果均具有显著性影响。即在限定时间区间内，随着拥堵扇区距离起飞机场的距离增加，拥堵扇区可用时间偏移量越大，航班通过调整速度和高度吸收延误的能力越强；随着空域拥堵程度的加深，到达目的机场的提前空间逐步减小，表明空域拥堵压缩了航迹优化的权衡空间。

图12 不同拥堵扇区和拥堵严重程度下航迹优化Pareto最优前沿解(三维)Fig.12 Pareto optimal frontiers with different congested sectors and severity of congestion (3D)

图13 不同拥堵扇区和拥堵严重程度下航迹优化Pareto最优前沿解(二维)Fig.13 Pareto optimal frontiers with different congested sectors and severity of congestion (2D)

为了进一步量化分析空域拥堵对于优化结果的影响，探究航空器燃油效率与空域拥堵时空特征的内在联系，采用评价指标HV论证Pareto前端解优劣，示意图如图14所示。需要注意的是，在计算HV时，应对数据进行归一化处理。

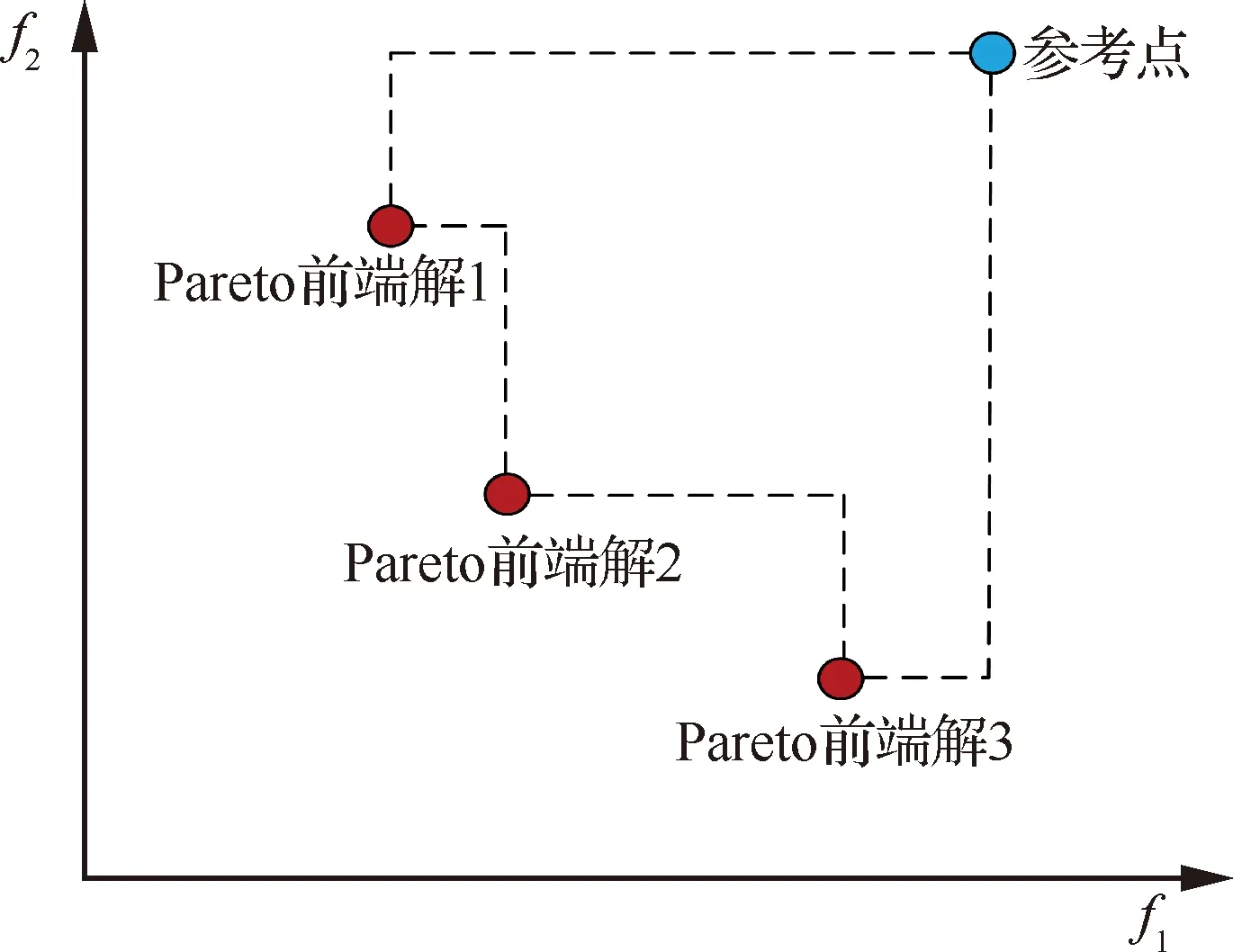
图14 超体积示意图Fig.14 Schematic diagram of hypervolume

本文选择归一化之后的(1,1)作为参考点，HV计算结果如表8所示，不同空域拥堵程度下“最优”扇区与起飞机场之间的距离变化如图15所示。总体上，随着拥堵扇区距离起飞机场距离增加，拥堵程度较小和中等时(时间偏移量为2～6 min)，燃油效率先增大后减小，航班分别在Sector2、Sector3、Sector4受限时获得最优性能，表明在可用时间区间内，利用中间扇区吸收延误航班能够获得最优性能。其原因在于，受限扇区与起飞机场的距离较小时，尽管航班有更长的剩余飞行距离恢复延误，但由于可供航班机动的飞行距离较短，航班通过调整垂直剖面和飞行速度吸收延误的能力有限，燃油效率无法达到最优；拥堵扇区与起飞机场的距离较大时，尽管起飞机场距离拥堵扇区的距离增加使航班吸收延误的能力增强，但较短的剩余飞行距离限制了航空器通过调整垂直剖面和飞行速度获取更优性能。当空域拥堵程度较大时(时间偏移量为8～12 min)，性能最佳的扇区总是Sector9，表明在限定时间区间内，将接近目的机场扇区的空域资源分配给需要在单一扇区延误8 min以上的航班时，可以提高飞行效率和燃油效率。同时，除Sector9外其余Pareto前沿都非常紧缩，表明当航班需要在中间单一扇区延误8 min以上，只通过调整高度和速度剖面推迟航空器进入扇区的时间并满足时效性约束这一方式几乎到达了极限，要吸收更大程度的延误必须采取地面等待、空中等待和改航等其余流量管理策略。

表8 HV计算结果Table 8 HV calculation results

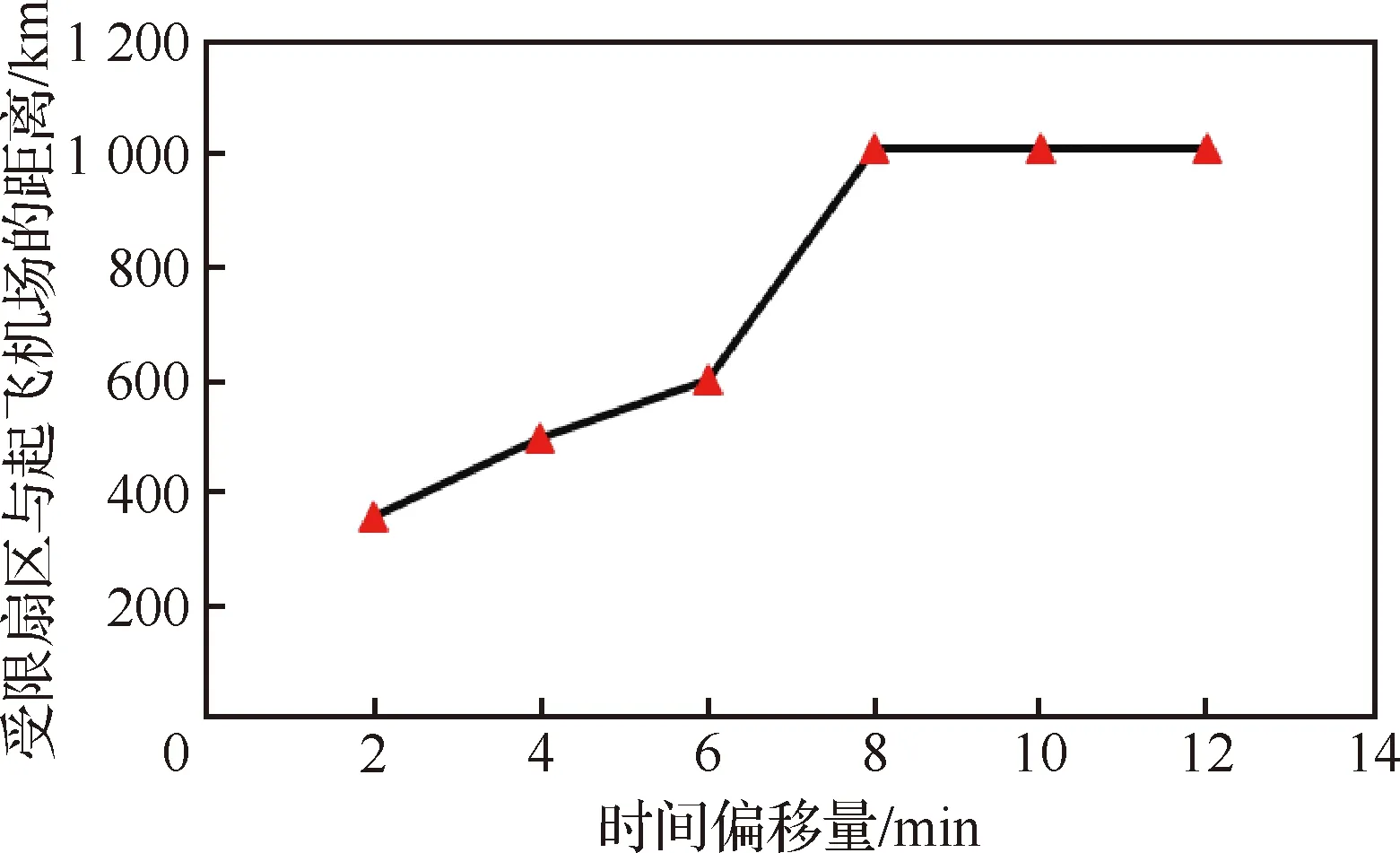
图15 不同空域拥堵程度下最优Pareto前端对应的拥堵扇区距离起飞机场的距离Fig.15 Distance from congested sector corresponding to optimal Pareto frontiers to departure airport under different airspace congestion levels

综上，本场景通过改变拥堵扇区的空间位置、拥堵扇区可用时隙与航班计划到达时间的偏移量得到不同的Pareto前端解，通过分析Pareto前端解在二维、三维空间中的特征及建立Pareto前端评价指标，探究了空域拥堵程度的时空特征对于航班性能的影响，验证了根据空域拥堵的时空特征规划合理航班四维航迹对于燃油效率具有改善作用，为准确地根据空域拥堵程度分配延误、提高城市对飞行燃油效率提供了方法。

7 结论与展望

本文面向航空精细化、系统化发展需求，基于跑道至跑道四维航迹模型和燃油消耗模型，采用水平轨迹离散化方法，以航班飞行时间和油耗作为优化目标，建立四维航迹优化模型及其高效求解算法，为航班规划空域资源受限时的飞行航迹，探讨了空域拥堵程度的时空特征对于航空器性能的影响，主要研究结论包括：

1) 在容量限制交通场景下，容量受限压缩了飞行航迹的权衡优化空间，更为灵活的水平运行空间有助于提升燃油消耗改善潜力，且航迹优化潜力对于航班进入容量受限扇区的计划到达时间与控制到达时间的差异具有显著的敏感性。

2) 航迹优化的结果对于空域拥堵的位置和严重程度具有显著的敏感性。总体上，在可用飞行时间区间内，起飞后最大可接受的扇区进入时间延误随拥堵扇区距离起飞机场越远而提高。当延误(小于6 min)出现在飞行水平路径中间时，航空器可以获得最优性能。

本论文为在TBO理念下规划容量受限时城市对间的飞行航迹提供方法基础，下一步考虑将研究范围从单一城市对扩展到更大范围的城市对航线网络，将宏观容流约束和微观间隔约束纳入航迹优化模型中。此外，由于气象条件与航空器性能密切相关，本文所建立的模型中暂未考虑高空风等气象要素，在后续研究中计划采用我国历史气象数据，将高空风的概率影响纳入航迹多目标优化模型中。