基于叶端定时的转子碰摩故障诊断方法
王维民,陈子文,张旭龙,陈康
1. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029 2. 北京化工大学 发动机健康监控与网络化教育部重点实验室,北京 100029
在现代工业中,航空发动机向着低损耗、高性能的方向发展,转子与静子间的间隙也在不断减小,发生转静碰摩故障的可能性也随之增加。为避免因故障产生更严重的灾难性事故,实现及时、准确的故障预警显得尤为重要。
以往对航空发动机转静碰摩诊断的研究主要集中在弯曲振动的变化特征上,分别在动力学建模、仿真、实验等方面进行了广泛的研究,碰摩会产生较宽频带范围的弯曲振动响应,随着转子运转,碰摩重复出现,产生的周期成分可作为碰摩故障诊断特征。而对碰摩引起扭转振动变化的研究相对较少,航空发动机转静碰摩是一个短暂的瞬态过程(在短时间内高加速度、瞬时力、瞬时扭矩),其中还涉及摩擦和扭转效应,摩擦产生的瞬态扭矩也不容忽视,瞬态扭矩的大小与碰摩半径和碰摩表面摩擦系数有关,方向与转子涡动方向有关(一般与转子旋转方向相反),相当于在转子上施加了额外的瞬时负载,由于航空发动机通过高压气流与燃油混合燃烧后产生高温燃气作为驱动,转速控制存在延迟,面对碰摩产生的反向力矩,发动机很难迅速控制转子转速,所以碰摩时航空发动机转速变化也是明显的。文献[12] 针对某型航空发动机试验过程中出现异响并伴随低压转子转速掉转的问题进行排故,结果确定为发动机低压涡轮单元体发生了转静碰摩故障。Roques等认为碰摩导致转子角速度较小与碰摩表面摩擦系数有关,当摩擦系数达到某一阈值后,观察到转子向后涡动现象,随摩擦系数增大,转子会出现迅速停止的现象。焦旭东总结出航空发动机转子碰摩故障振动信号特征为振动幅值出现明显的跳跃现象,此外振动相位波动也较为明显。Ma等通过建立双转子-机匣动力学模型分析了由碰摩诱发双转子机匣系统的振动响应,发现在相同碰摩工况下扭转振动幅值大于横向振动幅值。廖明夫等针对航空发动机碰摩导致转速波动、引起弯扭耦合振动的问题做了研究,结果发现由于延迟控制力矩的存在,碰摩导致转子扭转振动会产生持续较大的幅值,在一定情况下还会出现扭振失稳的现象。随后还有学者研究发现碰摩引起扭转振动的变化比弯曲振动更为明显,提出可以用扭转振动的变化诊断碰摩故障。随着叶端定时(Blade Tip Timing,BTT)法的发展,通过叶端定时监测叶片振动的应用日益广泛,监测结果的可靠性也得到了显著的提升,翟功涛等提出了以理想叶轮为假设的转子扭转振动监测方法,将叶端定时法运用在转子扭振的监测中,但并未通过分析扭振进行碰摩故障的诊断。
基于以上研究背景,提出了基于改进叶端定时法的转子碰摩故障诊断方法,在采用叶端定时法测量转子扭振过程时,考虑初始叶片加工装配和叶片振动导致叶片间距误差的影响对测量结果进行修正。通过实验研究与编码器结果比较验证所提改进叶端定时法的正确性,判断该方法是否可实现碰摩故障诊断。
1 碰摩诊断及测量方法
前文介绍了可通过转速波动和扭转振动进行碰摩故障的诊断监测,而对轴系转速波动和扭转振动的表述具有相同的量纲,能实现同源测量。对于转速波动,简单来说就是转速的动态偏差,在转子升速过程中,某些时段转速会出现较明显的波动,这是由于扭转振动越过转子扭转固有频率(Torsional Natural Frequency,TNF)引起的,通过去除旋转速度的直流分量可得转速波动变化情况。扭转振动则是沿旋转轴发生的角振动。需用两个传感器测量转子轴向两截面间扭转角度差(瞬时转速测量法),如要测量扭转高阶模态还需要更多的传感器测量转轴的静态扭转。由于转子角运动矢量符合叠加原理,转轴各质点的线运动具有相位调制现象,所以可通过测量瞬时角速度提取扭振信息。
1.1 BTT法测扭振
基于BTT法测量转子扭转振动是一种非接触式测量方法,其原理是测量叶尖扭转线速度进而提取扭转振动信息。如图1所示,图中为弯曲振动竖直方向振动速度,l和r分别为左、右侧传感器上升沿触发时间;为叶轮的旋转的角速度。传感器测量模拟叶轮的信号包含两个部分,转子自转线速度和横向振动速度,为消除横向振动的影响,在模拟叶轮的外壳上安装两个传感器(周向间隔180°)测量每个叶尖的瞬时相位(类似一个键相信号),当叶尖通过传感器时产生高电平信号,否则产生低电平信号。

图1 扭振测量示意图Fig.1 Schematic diagram of torsional vibration measurement
对原始模拟信号以高频计数频率进行计数,如果信号达到正向触发电压时,计数器输出为1,同时记录上升沿对应时序(=1,2,…,+1;=1,2,…),其中为脉冲数;为叶片数;为叶轮旋转圈数。当信号达到负向触发电压时,计数器输出为0,记录此刻下降沿对应时序。重复上述过程即可得到一系列方波信号,其相邻两个脉冲上升沿(即相邻两叶片)之间的时间间隔可表示为Δ=(+1-)(=1,2,…,),则左右传感器测得的时间间隔分别为

(1)

(2)
式中:为叶片数目;为转子瞬时角速度,=1,2,…,-1;为叶尖半径。
如果忽略叶片振动和叶间制造误差(认为叶片为理想周向均布的),转子瞬时角速度可表示为

(3)

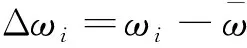
(4)
式中:Δ为波动角速度。
对波动量时域积分得到角位移形式的扭转振动,第-1个和第个脉冲间扭角变化值为

(5)
式中:为积分时间;为时间变量。
合并式(1)~式(5)得到脉冲时间差与扭转角关系:

(6)
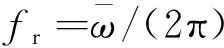

(7)
式中:“·”表示向下取整;为参数,取值通常大于4。
由于扭角信号采样是通过高频计数器实现的,所以扭角精度只取决于转频:

(8)
同时测量频率精度也是由输入信号频率和计数频率确定的:

(9)
通过提升(=)与能提升信号分辨率与质量,如同时采用脉冲信号上升沿与下降沿参与计算、增加传感器数量、提高计数频率等。
1.2 改进BTT法
1.1节介绍的测量方法在计算瞬时角速度时认为叶片在叶轮上的分布是理想的且叶片未发生振动,然而实际叶轮由于加工安装误差很难保证叶尖间距一致,且当叶轮运行至谐振转速时叶片会发生谐振,这均会导致相邻叶片通过传感器时扫过的弧长不为定值。如果采用理想叶尖间距参与计算,则会产生由于叶尖间距不相等引起的阶域和随机噪声干扰,这种误差模式随叶轮旋转在每一圈重复出现,因此其保持常数并独立于平均轴速度或扭转振动信号。所以可利用误差的平稳性识别由叶尖间距变化引起的误差结果,确定每旋转一圈产生的误差后,就可从测量结果中解析去除。由叶尖间距误差产生的时间误差(单个传感器)可表示为

(10)
式中:Δ(,)为叶尖间距;(,)()为叶片振动位移;为叶轮旋转频率,=/(2π);为叶片编号,=1,2,…,。
对于理想叶轮在没有叶片振动情况下叶片达到时间与角度差应是完美的线性关系,但是由于加工安装误差,叶片在实际叶轮上的安装角度会有所不同,即叶尖间距是非均匀的。当叶轮运行在低速或远离共振区域时,因叶片的动态特性,叶片振动通常是非常小的,甚至可认为其振动幅值为0,在这种情况下,实际叶尖间距误差Δ((,+1),)与实际叶片安装角误差Δ((,+1),)的关系为
Δ((,+1),)=Δ((,+1),)
(11)
当叶轮运行至谐振转速时,叶片振幅对测量的影响也不容忽视。可采用单自由度(Single-Degree-of-Freedom,SDOF)叶片振动分析方法分析识别叶片同步振动参数,叶片振动响应可表示为

(12)

(13)
式中:为叶片静态振动位移;为品质因数,=1/(2),其中为阻尼比;为叶片谐振频率;′为中间变量;为叶片振动相位,=+,其中为振动初始相位;为叶片振动直流分量。当≅时,叶片发生谐振,振幅达到最大,可表示为

(14)
根据式(10)经整周计算就能得到每个相邻叶尖间距产生的时间误差。为避免出现意外的误差,可增加计算圈数多次计算得到平均值。为方便计算可先确定每个叶尖通过传感器产生脉冲段的时间通过占比,假设轴每转一圈的速度保持不变,则脉冲段的归一化时间占比为

(15)
式中:()为叶轮第次旋转时的第个叶片时间通过比;(-1)+为第次旋转时的第个叶片旋转第圈的通过时间;为叶轮旋转一圈的归一化周期,即旋转一圈所用的时间。对于旋转圈对应的通过时间占比可取平均值,最终得到修正时间序列:

(16)

(17)
式中:Δ()为传感器测量得到的个叶片通过时间间隔。
采用式(16)的计算结果对式(1)和式(2)进行修正,代入式(6)计算扭转振动,就可去除叶尖间距不一致引起的计算误差。
2 仿真研究
为说明间距误差对扭振测量结果产生的影响,不考虑叶片振动设定仿真。假设叶轮(30个叶片)以10 Hz低速稳定运转,如果不发生扭转振动,叶轮转角=以恒定旋转角速度=20π rad/s 的速度线性持续增大。当发生扭振时,转子转角在的基础上叠加了扭转角分量,这是由于转子表面各质点的线运动具有相位调制现象,且旋转振动与扭转角振动均为矢量,根据矢量叠加原理,扭转角位移可表示为
=+sin(+)
(18)
式中:为扭振角幅值;为扭振频率;为扭振初始相位。
扭转振动可写为多阶模态相加的形式,为方便结果显示,只考虑一阶情况。设定式(18)中扭振角幅值=0.08°;扭振频率=8 Hz;扭振初始相位=0;设定13号叶片安装角误差Δ=0.015°,其余叶片都为均匀分布。采用BTT法测量扭转振动是等角度采样的,根据采样定理可知本仿真设定的采样频率/(2π)满足采样定理要求。仿真结果如图2所示。
当叶尖间距理想时BTT法能较精确地测量轴转速与扭转振动信号,当叶尖间距(13号叶片)存在误差时计算转频值出现了较大波动,与实际值差距较大。采用改进BTT法对叶尖间距误差进行识别,结果如图3所示,根据式(15)和式(17)再计算得到叶轮中每个叶尖间距的周长占比(取旋转50圈的数据参与计算),可看到13号叶片相邻间距出现较大变化,其余均为定值。随着叶轮旋转,这种误差会周期地出现,但其误差模式相对固定。根据式(16)采用改进BTT法对其进行修正(图2中只显示误差修正部分),结果表明该修正方法可去除由非均匀间距导致的转频计算误差。

图2 计算转频与修正结果(有间距误差)Fig.2 Calculated frequency and corrected results (with spacing error)

图3 叶尖间距误差识别Fig.3 Recognition of blade tip spacing error
图2和图3的仿真仅考虑了单个叶片安装误差,而实际叶轮可能每个相邻叶片均会有误差且在运行的过程中叶片会振动,对应图2中每一个计算转频均会出现较为明显的波动,使有效原始信号淹没在误差中。所以采用BTT法测量扭转振动时,叶尖间距误差与叶片振动误差均需纳入计算分析中。
3 实验研究
对改进BTT法进行实验验证,如图4所示,实验台主要由伺服电机、弹性联轴器、两个平衡盘、模拟叶轮及其他附件组成,最高转速为5 000 r/min。在模拟叶轮(30个叶片)叶顶间隔180°安装两个光纤传感器测量转子扭转振动(消除弯曲振动影响)。在转子末端安装一个增量式编码器,脉冲数(pulse/r,PR)为512,即转子每旋转一周产生512个脉冲信号,作为BTT法扭振测量的验证信号。实验过程中,转静碰摩发生在平衡盘1位置,通过调整竖直方向树脂碰摩螺钉和平衡盘之间的间隙模拟碰摩故障。图5为实验台转子模型示意图,碰摩螺钉用碰摩刚度和阻尼表示。

图4 转子实验台Fig.4 Rotor test rig
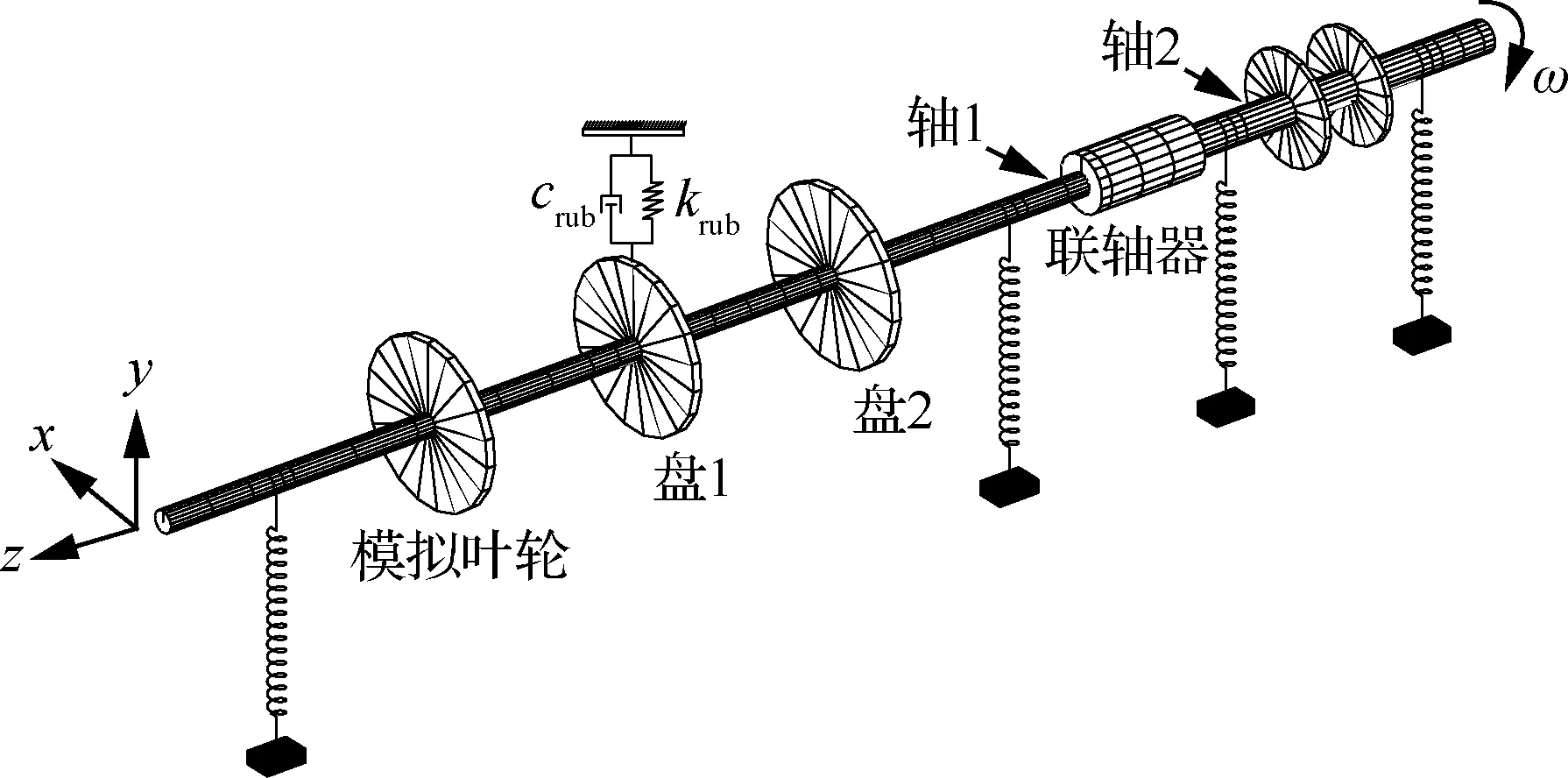
图5 轴系模型示意图Fig.5 Diagram of shafting model
通过动力学计算得到实验台轴系前两阶弯曲临界转速分别为3 154、10 369 r/min,前三阶扭转临界转速分别为6 323、11 762、18 932 r/min。由于实验台条件限制,选择两组转速(1 800 r/min和4 500 r/min) 进行实验,转子稳定旋转后分别施加两种碰摩工况:持续碰摩(工况1)和短时碰摩(工况2)。实验过程中,当转子在目标转速下稳定旋转时,按工况1施加碰摩,维持一段时间后结束碰摩。待转速平稳后再次按工况2施加碰摩,连续4次,记录上述实验数据。升高转速继续重复上述步骤,直到完成实验。
图6为1 800 r/min转速下实验误差识别与修正结果,从叶尖间距误差结果看,叶尖间距误差是明显的。每相邻叶尖间距变化都不同,由仿真结果可知,单个叶片误差会导致结果出现异常波动,采用原始BTT法每一步都存在计算误差,这会使计算结果与实际有较大差别。采用改进BTT法对结果进行修正,处理后的转速变化比原始结果小得多。根据结果比较可知,较小的叶尖间距误差足以引起较大的结果误差。

图6 转速为1 800 r/min时的误差识别与修正Fig.6 Error identification and correction for rotation speed of 1 800 r/min
为验证修正结果的可靠性,将改进处理结果与转子末端编码器数据进行对比,结果如图7所示。由碰摩引起的转速波动较为明显,且都被改进BTT法和编码器监测到,图7(a)、图7(b)和图7(d)、 图7(e)转速波动幅值也较为接近。放大碰摩段,并将其分为无碰摩、碰摩和脱离碰摩3个过程,碰摩时转速瞬间出现掉转现象,随后出现大幅振荡,当脱离碰摩后,转速出现低频振荡。截取此段数据对其进行频谱分析,结果显示不论是改进BTT法还是编码器结果都出现了超过工频幅值的低频振荡,编码器测得频率约为4.6 Hz,改进BTT法由于受频谱分辨率的限制,结果与编码器有细微差别,但不影响分析。脱离振荡结束后与无碰摩时波动幅值近乎一致。

图7 转速为1 800 r/min时的处理结果对照Fig.7 Processing result comparison for rotation speed of 1 800 r/min
图8为转速4 500 r/min时实验误差识别与修正结果,随转速变化,叶尖间距误差也在变化(叶片振动影响),同样采用改进BTT法处理,转速变化比原始结果小得多。与图6分析过程相同,将改进BTT法处理结果与编码器结果比较,如图9所示。可见改进BTT法仍然能很准确地监测到由碰摩导致的转速波动。与转速为1 800 r/min时的实验现象一致,在脱离碰摩过程时,出现了频率约为4.6 Hz的大幅振荡,其幅值远大于工频幅值。因实验台轴系是由电机驱动的,并采用弹簧联轴器连接轴1和轴2,电机和被驱动转子之间存在机电耦合作用,其中电机对轴系附加电磁刚度的作用会使轴系扭转固有频率出现偏移,使轴系除了本身存在的扭转“弹性”振动之外,还引入了额外的“刚体振动形式”,出现4.6 Hz的大幅振荡即为刚体振动频率。

图8 转速为4 500 r/min时的误差识别与修正Fig.8 Error identification and correction for rotation speed of 4 500 r/min

图9 转速为4 500 r/min时的处理结果对照Fig.9 Processing result comparison for rotation speed of 4 500 r/min
图6~图9的两组实验当碰摩发生时均出现了转速瞬时掉转,随后发生较大幅度振荡的现象,其原因可能在于电机控制。实验台驱动设备为电子换向式交流伺服电机,内置17 bit光学编码器进行精确调速,碰摩导致瞬间转速下降,电机内置编码器能精准反馈转子转速信息给控制器并与设定转速形成闭环控制,面对实际转子转速与设定转速出现的差异,控制系统能迅速做出反应进而增大电机输出扭矩,直到转速恢复到设定值时停止增大输出扭矩,但由于惯性作用,到达设定转速后转子仍然存在一定的加速度,导致转速超过设定转速,出现转速升高的情况。而航空发动机主要以高压气流与燃油混合燃烧后产生高温燃气作为驱动,转速控制比电机控制慢得多。理论上只要航空发动机碰摩导致的扭振响应频率在改进BTT法频率适用范围内(见式(7)),碰摩扭振信号即可被监测到,精度由式(8)与式(9)确定。
4 结 论
1) 采用基于BTT法测量轴系扭转振动时,叶尖间距变化会导致结果出现较大误差。
2) 提出的改进BTT法可识别由叶尖间距变化引起的计算结果误差,且能将其解析去除。
3) 改进BTT法能准确监测因碰摩导致的转速掉转与扭转振动变化,可用来诊断航空发动机碰摩故障。

