基于GIOWA 算子的我国货币需求水平组合预测研究
李 颖,庄科俊
(安徽财经大学统计与应用数学学院,安徽 蚌埠 233030)
0 引言
自1992 年开始,中国的经济就步入了快速增长的阶段.1992 年的国内生产总值为271945.53 亿元,到2020 年国内生产总值达到1015986.20 亿元,28 年间总增速达到273.6%,每年的平均增速达到9.77%.即便在2020年全球新冠疫情爆发的不利环境下,中国仍然在全球经济萎缩4.4%的情况下保持2.3%的增长.在国内经济增长的同时,消费需求也会随之增加,进而导致国内货币需求的增加.我国广义货币供应量从1995 年的60750.5 亿元增长到2020 年的2186800 亿元,增长了近36 倍,每年的平均增长速度为139.99%.只有在货币供给与货币需求相适应时,经济才会避免通货膨胀和通货紧缩而达到稳定增长的状态[1].因此很多学者都在基于不同的模型研究各国的货币需求,从而为本国货币政策的制定提供参考.Jalaee Sayyed Abdolmajid[2]等学者通过考察伊朗的真实流动性、消费价格指数、GDP、贷款利率、通货膨胀率和官方汇率六个指标,合理利用BBO、PSO 和基于生物地理优化的粒子群优化方法BBPSO计算伊朗的货币需求.在国内研究中,刘峰[3]根据1999—2005 年实际货币需求量构建灰色模型GM(1,1)预测我国货币需求量;戴国强[4]选取1979—1986年的国民收入、社会总产值和工农业总产值为解释变量,分别建立线性回归模型对我国的货币需求量进行预测.纵观国内外现有研究,有关货币需求的预测研究主要有两种方式:一是通过外生变量对其拟合;二是根据历史数值预测未来水平.首先,直接或间接影响本国货币需求量的因素包括通货膨胀的差异、利率与汇率的差异、政治稳定和经济表现等因素.很难通过观测这些因素的整体表现来更好的预测货币需求水平及其波动性[5].其次,通过分析过去几年的数据来预测货币市场忽视了其他因素对货币需求产生的影响.故而本文选择建立组合模型将上述两个模型纳入一个框架内,用以预测我国未来的货币需求水平.组合模型广泛的运用于各种经济变量的预测中,例如我国居民消费水平[6]、中国GDP[7]、浙江省GDP[8]、河北省能源消费量[9]以及蔬菜价格[10]等.
本文选取1995—2020 年广义货币供给量、国内生产总值及货币流通速度构建多元回归模型、ARIMA(1,1,2)模型和Holt-Winters 无季节模型,基于上述三个模型构造使对数误差、相对误差、0.5 次幂误差和0.25 次幂误差平方和最小的GIOWA 算子组合预测模型,对我国2021—2023 年的货币需求量进行预测,并对模型进行有效性评价,对比不同诱导因子的预测精度及各项预测误差.
1 模型简介
1.1 GIOWA 算子
定义1(GIOWA 算子)存在n个维数组(〈α1,β1〉,〈α2,β2〉,…,〈αn,βn〉),令与GIOWAW相对应的权重向量为

对诱导因子(α1,α2,…,αn)进行降序排列,则GIOWA 算子计算的表达式为

其中,α-index(i)表示诱导因子的逆序排列的下标.
1.2 GIOWA 组合预测模型
假设组合预测模型有n(n≥2)种方法.令时间t的实际观测值为xt,第i个单项预测方法在时间t的预测值为xit;git表示方法i在时间t的λ次幂误差wi表示第i 种方法占模型的权重).W为n维权重向量,Rn=(1,1,…,1)T,可知,则样本期内预测值及λ次幂误差的计算公式分别为:
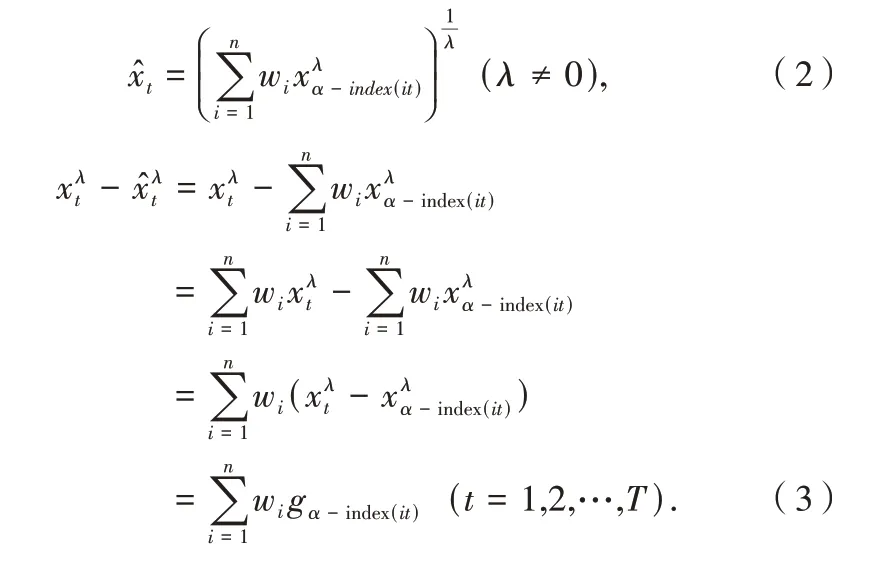
如果诱导因子αit(i=1,2,…,n;t=1,2,…,T)选择第t期用第i种预测方法的预测精度,则αit的表达式为:

于是GIOWA组合预测模型的预l次幂误差平方和为:
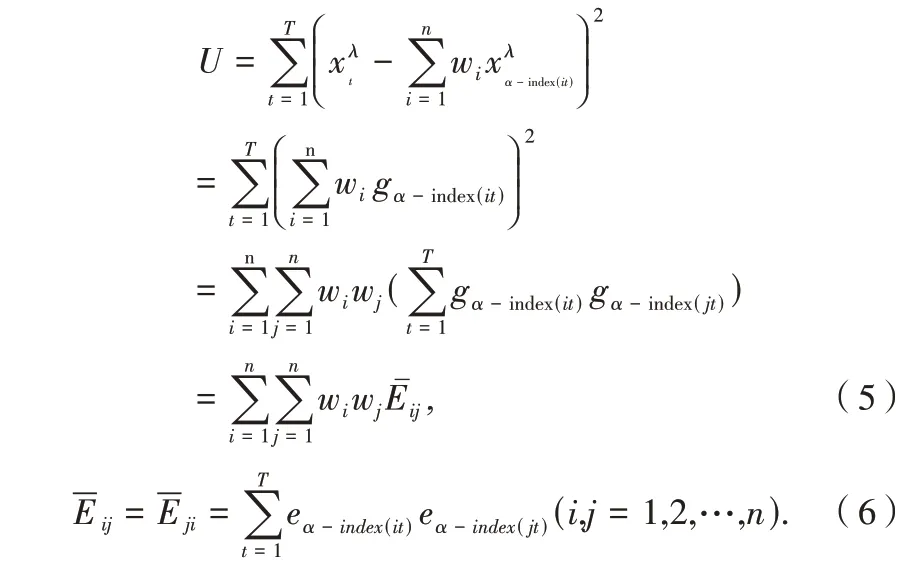
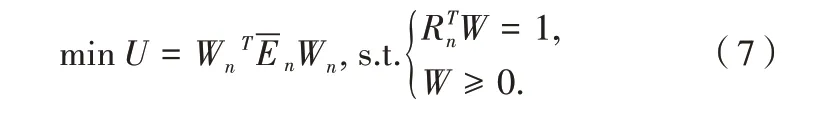
1.3 模型评价体系
建立(GIOWA)算子组合预测模型评价体系,详见表1.

表1 误差评价体系
2 实证分析
2.1 数据来源与描述性统计
本文采用M2 作为衡量我国货币需求的变量,即被解释变量的时序图如图1 所示.由图可知我国的货币需求量逐年增长,且在2008 年的增长幅度有个明显的提升.选取GDP、CPI、存款利率、长期货币流通速度四个指标作为解释变量.由于在多元线性回归模型中,采用逐步回归法剔除利率与长期货币流动速度两个不显著的变量,得到如表2所示的模型的变量.

图1 实际货币需求量的时序图

表2 变量的定义与描述性统计
2.2 单项预测模型
2.2.1 多元回归模型
本文选取1995—2020 年我国实际货币需求水平作为多元回归模型的被解释变量,解释变量为GDP 和CPI.通过对残差项进行白噪声检验可判定其存在协整关系.为了规避出现异方差的情况,将M2 及GDP 取自然对数,由于CPI是平稳的序列.多元回归模型表达式:

在模型的拟合优度为0.9985 及所有变量均通过t检验与P值均小于0.000的情况下,对模型做如下检验:首先,由于检验的结果P 值为0.2610 通过异方差检验.其次,VIF 均为1.2 故不存在多重共线性.最后,由内生性检验结果知P值为0.3901,大于0.05.故可以排除内生性的影响.
2.2.2 ARIMA 预测模型
因实际货币需求量的时序图可知该序列是不平稳的,故取M2 的自然对数并做一阶差分,得到的序列在第三期后序列的自相关函数均进入临界域内,所以DLNM2是平稳的时间序列.故所以ARIMA(p,d,q)中的d取1.对DLNM2 做自相关与偏自相关分析可得:由PAC-AC 图知此模型ARIMA(p,d,q)中的p值选1,q值选2.根据检验可知,该序列并非白噪声序列.最终确定ARIMA(1,1,2)模型,用DLNM2对AR(1),MA(2)进行回归可知该ARIMA(1,1,2)模型公式:

查表得在1% 的上下界中dL=1.22,dU=1.55,dU=1.55 ≤D.W.=1.8483 ≤4 -dU=2.45.故该模型不存在自相关,根据该模型的t值P 值都显著.首先,由残差的ACPAC 图最右侧的一列的P 值都大于0.05,则说明是白噪声的.其次,模型通过T检验.再次,ARIMA 多项式的特征根分布检验通过.最后通过对模型的残差序列进行Q检验,即残差序列不存在自相关性.至此,针对ARIMA(1,1,2)的四个检验全部通过.故所建模型是合理的.
2.3.3 Holt-Winters 无季节指数平滑模型
Holt-Winters 无季节指数平滑模型是可以预测无季节变化但有时间趋势数据的一种模型.Holt-Winters无季节指数平滑模型公式为

其中,α,β⊂(0,1) 表示阻尼因子.yt平滑后的模型为,其中at,bt分别为模型的截距和斜率.Holt-Winters 无季节指数平滑模型采用Stata15 软件对我国居民消费水平进行预测,结果见表3.

表3 三种单项预测模型的预测值与预测精度
2.3 组合预测模型
2.3.1 模型的构建
(1)当λ→0 时,建立GIOWA 组合预测模型

将三个单项模型按预测精度的大小重新排列,依据上述公式可得到对应的诱导有序对数误差信息矩阵为

以对数误差平方和最小为目标建立GIOWA 模型:
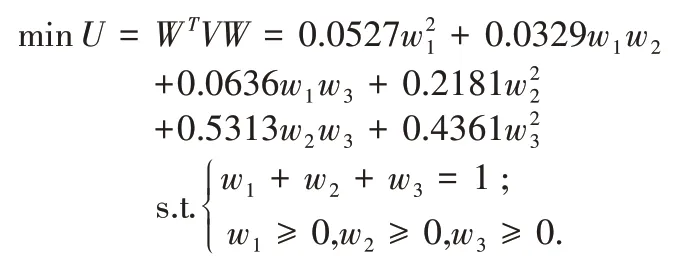
用Lingo10 求解,得权重:

则对应的GIOWA 组合预测模型为
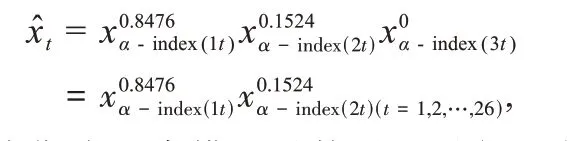
样本期内组合模型对数误差平方和为0.0471764.
(2)当λ=1 时,建立GIOWA 组合预测模型

将三个单项模型按预测精度的大小重新排列,依据上述公式可得到对应的诱导有序绝对误差信息矩阵为

构建以绝对误差平方和最小为目标的GIOWA 组合预测模型:
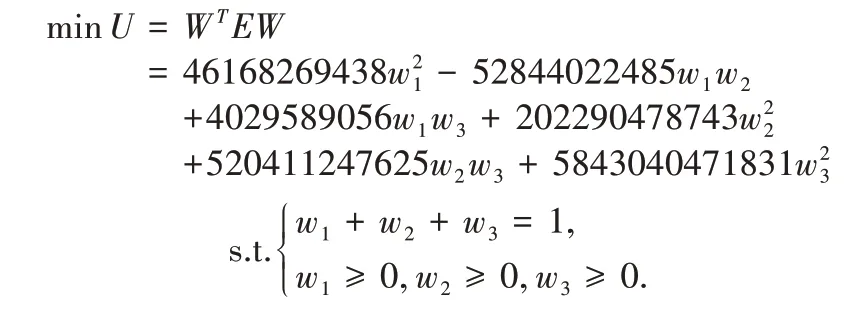
用Lingo 求解,得权重:

则对应的GIOWA 组合预测模型为

样本期内组合模型相对误差平方和为2868972.
(3)当λ=0.5 时,建立GIOWA 组合预测模型:

将三个单项模型按预测精度的大小重新排列,依据上述公式可得到对应的0.5 次幂误差信息矩阵为:

建立GIOWA(λ=0.5)组合预测模型:

用Lingo 求解,得权重:

则对应的GIOWA(λ=0.5)组合预测模型为:
样本期内组合模型0.5 次幂误差平方和为7207.352.
(4)λ=0.25 时,建立GIOWA 组合预测模型:

将三个单项模型按预测精度的大小重新排列,依据上述公式可得到对应的0.25 次幂误差信息矩阵为:

建立GIOWA(λ=0.25)组合预测模型:

用Lingo 求解,得权重:

则对应的GIOWA(λ=0.25)组合预测模型为:

样本期内组合模型0.25 次幂误差平方和为2.137528.
根据上述四个模型求出的不同精度模型对应的权重,将其汇总到表4.
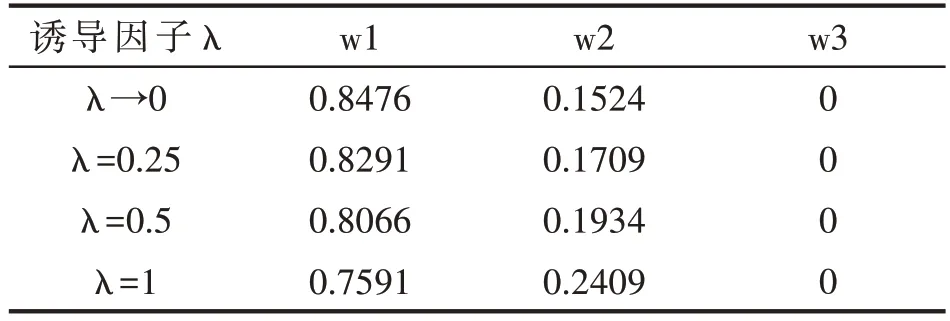
表4 λ 不同取值时权重变化表
由表4 可以看出,随着λ 的增加,组合预测模型赋予诱导最高的模型的比重渐渐降低,而赋予诱导精度次高的模型的权重渐增,赋予预测精度最低的模型的比重始终为0.
至此,根据上述四种不同的诱导因子取值得到如表5 所示的GIOWA 算子组合预测模型的预测值及其预测精度:
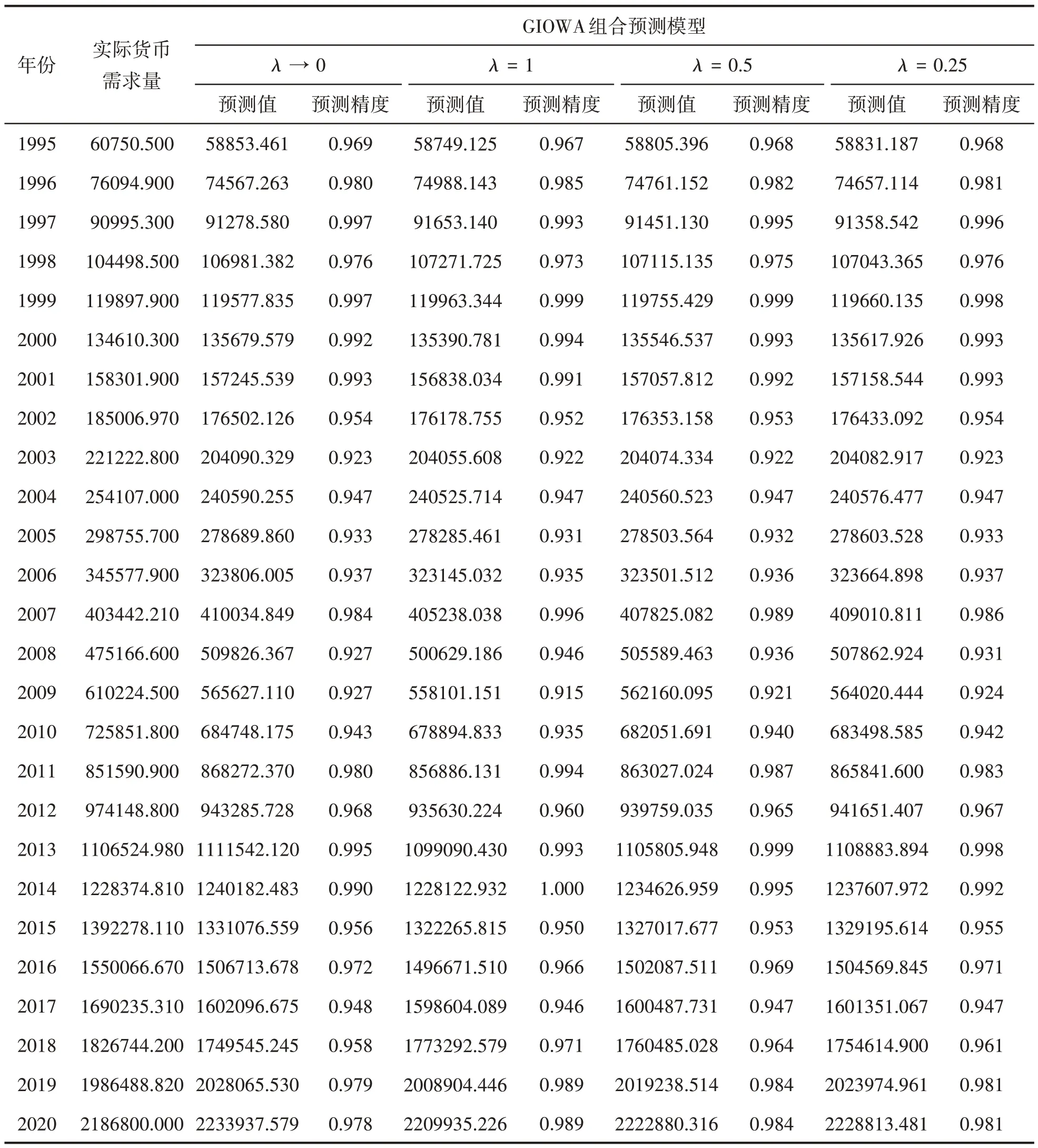
表5 GIOWA组合预测模型的预测值与预测精度
2.3.2 模型评价
计算多元回归模型、ARIMA(1,1,2)模型、Holt-Winters无季节模型以及广义诱导组合预测模型四个模型的预测精度、各项误差并对其进行归一化处理可到表6.由表6 可知组合预测模型的预测精度均在96%以上,单项预测模型中的ARIMA(1,1,2)模型的预测误差相对最大的,Holt-Winters 无季节模型的预测误差是最小的.在GIOWA 组合预测模型中λ=1 的组合预测模型表现较好,各项误差为最小值的概率最大,其次是λ=0.25.其中λ→0 的组合预测模型的表现相对来说是最不好的,预测误差最大且预测精度最低.组合预测模型中预测精度的排序依次为:λ=1 ≻λ→0 ≻λ=0.5 ≻λ=0.25.因此用GIOWA 组合预测模型可以较好地预测我国货币需求量,其中诱导因子λ=1 时的组合预测模型相对其他诱导量的模型来说预测精度最高且预测误差最低.诱导因子λ→0 时的组合预测模型相对其他诱导量的模型来说预测精度最低且预测误差最高.可知在预测我国实际货币需求量的组合预测模型时,最好的组合预测方法为诱导因子λ=1 时,而最差的组合预测方法是诱导因子λ→0 时的组合预测模型.

表6 各项模型误差比较
2.3.3 预测结果
根据上文求出的各单项模型的权重,对其进行算术平均可得到各单项预测模型对组合预测模型的贡献.分配给多元回归模型、ARIMA(1,1,2)模型以及Holt-Winters模型的权重分别为0.524、0.241 和0.235.预测计算公式为:

根据上述公式求出GIOWA模型的预测值如表7所示.
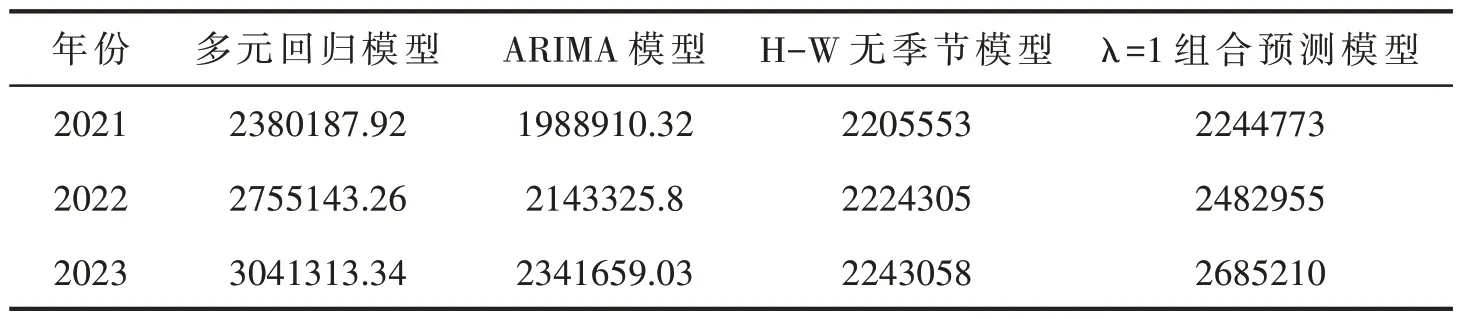
表7 单项模型及组合预测模型的预测值
3 结语
本文通过构建以多元回归模型、ARIMA (1,1,2)模型以及Holt-Winters 无季节模型为三个单项预测模型,广义诱导因子选取趋向于0、1、0.5 以及0.25 四个值的GIOWA 算子组合预测模型,基于1995—2020 年的样本数据预测未来三年我国实际货币需求量水平.研究结果表明,GIOWA 算子组合预测模型在文章提出的四种预测模型中预测精度最高、模型误差最低.组合预测模型的预测精度均在96%以上.由图2 可知,诱导因子λ 为1时的组合预测模型最贴近真实值,该模型相对其他诱导量的模型来说预测精度最高且预测误差最低.基于GIOWA 算子组合预测模型预测未来三年我国实际货币需求量水平将会保持稳速增长,依据诱导因子为1 的模型预测未来三年我国实际货币需求量的预测值分别为2244772.589、2482954.835、2685209.767(单位:亿元),增长幅度分别为2.651%、10.611%和8.146%.我国实际货币需求水平整体呈现出上升的趋势,在2021 年会有一个缓和的上升,在2022 年会出现一个波动上升,然后上升幅度会在2022 年之后加下降.增长幅度会是一个先上升后下降的过程,建议应避免在2021 年出现通货紧缩而在2022 年出现通货膨胀的现象.

图2 实际货币需求量与各模型预测值

